TEMA: DESEMPE˜NO Especificaciones de desempe˜no

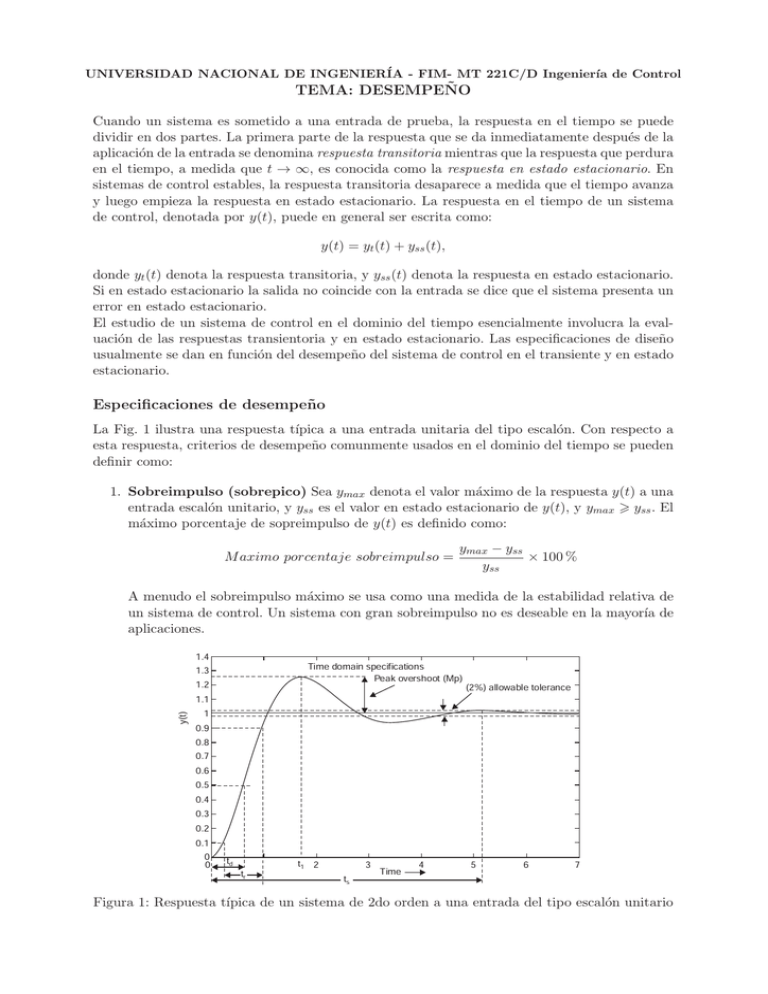
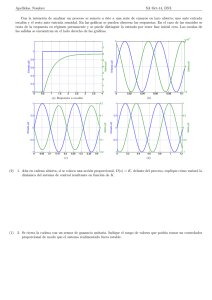
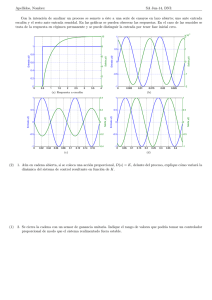
UNIVERSIDAD NACIONAL DE INGENIERÍA - FIM- MT 221C/D Ingenierı́a de Control
TEMA: DESEMPEÑO
Cuando un sistema es sometido a una entrada de prueba, la respuesta en el tiempo se puede
dividir en dos partes. La primera parte de la respuesta que se da inmediatamente después de la
aplicación de la entrada se denomina respuesta transitoria mientras que la respuesta que perdura
en el tiempo, a medida que t → ∞, es conocida como la respuesta en estado estacionario. En
sistemas de control estables, la respuesta transitoria desaparece a medida que el tiempo avanza
y luego empieza la respuesta en estado estacionario. La respuesta en el tiempo de un sistema
de control, denotada por y(t), puede en general ser escrita como:
y(t) = yt (t) + yss (t),
INTRODUCTION TO CONTROL ENGINEERING
92
donde yt (t) denota la respuesta transitoria, y yss (t) denota la respuesta en estado estacionario.
Si en estado estacionario la salida no coincide con la entrada se dice que el sistema presenta un
error en estado estacionario.
El estudio de un sistema de control en el dominio del tiempo esencialmente involucra la evaluación de las respuestas transientoria y en estado estacionario. Las especificaciones de diseño
usualmente se dan en función del desempeño del sistema de control en el transiente y en estado
estacionario.
Especificaciones de desempeño
4.4 PERFORMANCE SPECIFICATION OF LINEAR SYSTEMS IN TIME-DOMAIN
La Fig. 1 ilustra una respuesta tı́pica a una entrada unitaria del tipo escalón. Con respecto a
4.4.1 Transient Response Specifications
esta respuesta, criterios de desempeño comunmente usados en el dominio del tiempo se pueden
definir como:
1. Sobreimpulso (sobrepico) Sea ymax denota el valor máximo de la respuesta y(t) a una
entrada escalón unitario, y yss es el valor en estado estacionario de y(t), y ymax > yss . El
máximo porcentaje de sopreimpulso de y(t) es definido como:
M aximo porcentaje sobreimpulso =
ymax − yss
× 100 %
yss
y(t)
A menudo el sobreimpulso máximo se usa como una medida de la estabilidad relativa de
un sistema de control. Un sistema con gran sobreimpulso no es deseable en la mayorı́a de
aplicaciones.
1.4
1.3
1.2
1.1
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
Time domain specifications
Peak overshoot (Mp)
td
tr
t1 2
ts
3
Time
4
(2%) allowable tolerance
5
6
7
Fig.tı́pica
4.3 Typical
response
of ade
second
linear
system
with step
Figura 1: Respuesta
de un
sistema
2do order
orden
a una
entrada
delinput
tipo escalón unitario
2. Tiempo de subida El tiempo de subida tr es definido como el tiempo requerido por la
respuesta a una entrada del tipo escalón unitario par alcanzar del 10 al 90 % de su valor
final. (Algunos autores consideran del 0 al 90 % del valor final).
3. Tiempo de asentamiento El tiempo de asentamiento ts está definido como el tiempo
requerido por la respuesta a una entrada del tipo escalón unitario para decrecer y permanecer dentro de un porcentaje especificado de su valor final. Porcentajes frecuentemente
usados son 2 y 5 %.
Las cantidades antes definidas dan una directa medida de las caracterı́sticas de un sistema de
control en función de una respuesta al escalón unitario. Analı́ticamente estas cantidades son
difı́ciles de calcularse excepto por sistemas de orden menor a 3. A continuación se tomará el
caso de un sistema de segundo orden que permitirá ayudar con el análisis y diseño de sistemas
de orden alto.
Sistema de segundo orden
La ubicación de los autovalores de la matriz dinámica determina el comportamiento del sistema
en lazo cerrado, y como consecuencia, la decisión más importante es dónde ubicaremos los
autovalores.
Masa-resorte-amortiguador
En mecánica una de esas ecuaciones diferenciales más usadas es:
mq̈ + cq̇ + kq = u,
(1)
donde u representa el efecto de entradas externas. El modelo (1) es llamado ecuación diferencial
controlada o forzada. Cuando u = 0, el modelo se denomina ecuación diferencial libre. Este
modelo puede fácilmente representar un sistema dinámico tal como el sistema masa-resorte con
amortiguamiento, ver Fig. 2. La variable q ∈ R representa la posición de la masa m con respecto
a su posición de reposo. Se emplea q̇ para referirse a la derivada con respecto al tiempo de q
(velocidad de la masa) y q̈ para representar a la segunda derivada (aceleración). Decimos que
el sistema es de segundo orden dado que la dinámica depende de las dos primeras derivadas de
q.
q
c(q)
m
k
Figura 2: Masa-resorte con amortiguamiento
Un sistema de segundo orden en (1) puede ser reescrito como:
q̈ +
o, definiendo ωo2 = km y 2ζωo =
c
k
1
q̇ + q = u,
m
m
m
c
.
m
q̈ + 2ζωo q̇ + ωo2 q = kωo2 u,
y = q.
Donde la salida se considera como la posición q. En la forma de espacio de estados, el sistema
se escribe como:
dx
0
ωo
0
=
x+
u, y = 1 0 x.
−ωo −2ζωo
kωo
dt
Los autovalores del sistema están dados por:
λ = −ζωo ±
p
ωo2 (ζ 2 − 1),
y observamos que el origen es un punto de equilibrio estable si ωo > 0 y ζ > 0. Nótese que los
autovalores son complejos si ζ < 1 y reales en caso contrario.
La forma de la solución depende del valor de ζ, el cual se denomina factor de amortiguamiento
del sistema. Si ζ > 1, decimos que el sistema es sobreamortiguado, y la respuesta natural (u = 0)
del sistema está dado por:
βx1o + x2o −αt αx1o + x2o −βt
e
−
e ,
β−α
β−α
p
p
donde α = ωo (ζ+ ζ 2 − 1) y β = ωo (ζ− ζ 2 − 1). Vemos que la respuesta consiste en la suma de
dos señales que decaen exponencialmente. Si ζ = 1, entonces el sistema es crı́ticamente amortiguado
y la solución resulta:
y(t) = e−ζωo t (x1o + (x2o + ζωo x1o )t).
y(t) =
Nótese que la respuesta es aún asintóticamente estable mientras que ωo > 0, a pesar que el
segundo término en la solución este creciendo con el tiempo (pero más lento que el término
exponencial decayente que lo multiplica).
Finalmente, si 0 < ζ < 1, entonces la solución es oscilatoria y se dice que el sistema es
subamortiguado. El parámetro ωo es conocido como la frecuencia natural del sistema. La respuesta natural del sistema está dada por:
1
ζωo
−ζωo t
x1o +
x2o sin ωd t),
y(t) = e
(x1o cos ωd t +
ωd
ωd
p
donde ωd = ωo 1 − ζ 2 es llamada la frecuencia amortiguada.
Respuesta al escalón unitario
Debido a la forma simple de un sistema de segunda orden, es posible resolver el sistema en
forma analı́tica para una entrada del tipo escalón. Para este caso, la solución depende de ζ:
!
ζ
−ζωo t
−ζωo t
y(t) = k 1 − e
cos ωd t + p
e
sin ωd t , ζ < 1
1 − ζ2
y(t) = k 1 − e−ζωo t (1 + ωo t) , ζ = 1
!
√
√
1
ζ
ζ
1
−ζωo t(ζ− ζ 2 −1)
−ζωo t(ζ+ ζ 2 −1)
+ (p
, ζ > 1,
y(t) = k 1 − ( p
+ 1)e
− 1)e
2
2
1 − ζ2
1 − ζ2
donde hemos tomado x(0) = 0.
La Fig. 3 muestra respuestas de un sistema de 2da orden a una entrada del tipo escalón con
k = 1 y para diferentes valores de ζ. La forma de la respuesta es determinado por ζ, y la
velocidad de la respuesta es determinada por ωo : la respuesta es más rápida si ωo es grande.
Adicionalmente también podemos calcular las propiedades de la respuesta al escalón. Por ejemplo, para un sistema subamortiguado:
!
ζ
y(t) = k 1 − p
e−ζωo t sin(ωd t + ϕ) ,
1 − ζ2
donde ϕ = arccosζ. El sobreimpulso máximo ocurrirá por primera vez cuando la derivada de y
sea cero, que se puede mostrar que es:
√
2
Mp = e−πζ/ 1−ζ .
De la misma forma se pueden calcular otras caracterı́sticas de la respuesta al escalón, Cuadro
4.
185
6.3. STATE FEEDBACK DESIGN
2
Im
ζ = 0.4
ζ = 0.7
ζ =0
1.5
ζ =1
Re
y
ζ = 1.2
1
ζ
0.5
0
0
5
10
Normalized time ω0 t
(a) Eigenvalues
15
(b) Step responses
Figure 6.8: Step response for a second-order system. Normalized step responses h for the
Figura 3: Respuestas de un sistema de 2da orden a una entrada del tipo escalón unitario
Property
Value
Steady-state value
k
ϕ/ tan ϕ
Rise time
Tr = 1/ω0 · e
√
2
M p = e−π ζ / 1−ζ
Overshoot
Settling time (2%)
Ts ≈ 4/ζ ω0
ζ = 0.5
√
ζ = 1/ 2
ζ =1
k
k
k
1.8/ω0
2.2/ω0
2.7/ω0
16%
4%
0%
8.0/ω0
5.9/ω0
5.8/ω0
Figura 4: Propiedades de la respuesta al escalón para un sistema de 2do orden con 0 < ζ < 1.
Respuesta en frecuencia
La respuesta en la frecuencia también puede ser calculada explı́citamente y está dada por:
M eiθ =
kωo2
kωo2
=
(iω)2 + 2ζωo (iω) + ωo2
ωo2 + 2iζωo ω + −ω 2
Una ilustración gráfica de la respuesta en frecuencia está dada en la Fig. 5. Nótese que el pico
de la resonancia aumenta a medida que crece ζ.
186
CHAPTER 6. STATE FEEDBACK
Im ζ ≈ 0
ζ =1
10
Gain
ζ = 0.08
ζ = 0.2
ζ = 0.5
10
10
Phase [deg]
Re
2
−2
0
ζ
−90
−180 −1
10
(a) Eigenvalues
ζ
0
0
10
Normalized frequency ω/ω0
10
1
(b) Frequency responses
Figura 5: Respuesta en frecuencia de un sistema de 2do orden.
Sistema de orden alto representado por un sistema de 2do orden
Para sistemas de orden alto, la ubicación de polos es considerablemente más dificil, especialmente cuando tratamos de considerar las múltiples concesiones mutuas presentes en el diseño
de control por realimentación.
Una de las razones por las que los sistemas de segundo orden son tan importantes en los sistemas
de realimentación es que aún para sistemas complicados la respuesta es a menudo caracterizada
por los autovalores dominantes. Para definir los autovalores dominantes, consideremos el sistema con autovalores λj j = 1, ..., n. Definimos el factor de amortiguamiento para el autovalor
complejo como:
−Reλ
ζ=
.
kλk
Decimos que el par de autovalores complejos conjugados λ, λ∗ es un par dominante si tiene
el menor factor de amortiguamiento comparado con los otros autovalores del sistema. Por
consiguiente, se puede decir que el par dominante de autovalores será el factor principal en la
respuesta del sistema después que los transientes debido a otros términos (autovalores) hayan
desaparecido. A pesar de que esto último no siempre se cumple, a menudo el caso de los
autovalores dominantes determinana la respuesta (al escalón) del sistema.
El único requerimiento formal en la asignación de autovalores es que el sistema sea controlable.
En la práctia existen otras restricciones porque la selección de autovalores tiene un gran efecto
en la magnitud y la variación del cambio de la señal de control. Autovalores grandes requerirán
por lo general grandes señales de actuación ası́ como también rápidos cambios de estas señales.
La capacidad de los actuadores impondrá restricciones en la posible ubicación de los autovalores
del sistema en lazo cerrado.