Estudio-resumen de los sistemas homogéneos de dos

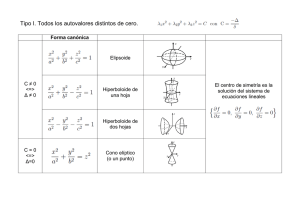
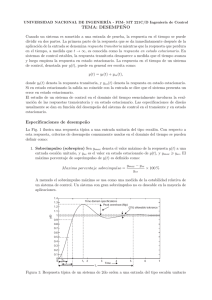
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
Estudio-resumen de los sistemas homogéneos de dos ecuaciones
diferenciales lineales con coeficientes constantes:
Sea el sistema
x’= a·x + b·y
y’= c·x + d·y
Para resolverlo en primer lugar se calculan los valores propios de la matriz del sistema.
Llamando a la traza de la matriz p  es decir, a+ d y al determinante de la matriz q  es
decir, a·d - b·c , la ecuación característica es:
r2 - p·r + q = 0
Los autovalores se obtienen de acuerdo con la fórmula de las raices de una ecuación de
segundo grado:
r = p ± √(p2 - 4·q)
El estudio de los autovalores sirve para clasificar el punto (0,0) del plano de fase y las
trayectorias del sistema.
1. q < 0.En este caso el radicando siempre es positivo por lo que los autovalores son
reales. Como q es el producto de los dos autovalores, ambos han de ser de signos opuestos.
El origen es un punto de ensilladura (saddle point).
2. q > 0.-
Se pueden plantear varios casos:
2.1. p2 > 4·q.
El radicando es positivo, por lo que los autovalores son reales y del mismo
signo pues el determinante, q, es positivo
2.1.1. p > 0. Los autovalores son positivos. El origen es un nodo inestable (unstable node).
2.1.2. p < 0. Los autovalores son negativos. El origen es un nodo estable (stable node).
2.2. p2 < 4·q.
conjugados.
El radicando es negativo, por lo que los autovalores son complejos
2.2.1. p > 0. En este caso la parte real de los autovalores es positiva. El origen es un punto
espiral inestable (unstable spiral point o spiral source).
2.2.2. p = 0. La parte real de los autovalores es nula. El origen es un punto centro (centre
point).
2.2.3. p > 0. La parte real de los autovalores es negativa. El origen es un punto espiral
estable (stable spiral point o spiral sink).
2.3. p2 = 4·q. La ecuación característica tendrá un autovalor doble del signo de p.
CAMPUS TECNOLÓGICO DE LA UNIVERSIDAD DE NAVARRA. NAFARROAKO UNIBERTSITATEKO CAMPUS TEKNOLOGIKOA
Paseo de Manuel Lardizábal 13. 20018 Donostia-San Sebastián. Tel.: 943 219 877 Fax: 943 311 442 www.esi.unav.es [email protected]
2.3.1. p > 0. El autovalor doble es positivo. El origen es un nodo inestable (unstable node).
Si hay dos autovectores linealmente independientes asociados al auutovalor doble, entonces
el origen es un punto manantial (source point o node source).
2.3.2. p < 0. El autovalor es negativo. El origen es un nodo estable (stable node). Si hay dos
autovectores linealmente independientes asociados al auutovalor doble, entonces el origen es
un punto sumidero (sink point o node sink).
3. q = 0.
Esto significa que el rango de la matriz del sistema es la unidad y, por tanto, la
segunda fila es múltiplo de la primera (c/a = d/b = k). Se puede observar, además, que el
punto (0,0) no es un punto crítico aislado del sistema, sino que todos los puntos de la recta y =
-a·x/b (suponiendo que b no es nulo) son puntos críticos del sistema. Las trayectorias en el
plano de fases son las rectas y = k·x + E, siendo E una constante.
3.1 p > 0
Las trayectorias empiezan en los puntos críticos y terminan en el infinito.
3.2 p > 0
Las trayectorias terminan en los puntos críticos, proviniendo del infinito.
El plano traza-determinante
Un modo de representar cada uno de los casos estudiados previamente y, sin necesidad de
obtener los autovalores es definir un plano cuyo eje de abscisas sea la traza de la matriz del
sistema y el eje de ordenadas el determinante. La posición del ‘punto’(p,q) que representa al
sistema nos da información del origen de coordenadas en la plano de fases y de las
trayectorias del sistema. Basta para ello representar en dicho plano la parábola q = p2/4
Punto espiral
estable
Punto espiral
inestable
centro
Nodo estable
Nodo inestable
Punto de ensilladura
En función de la posición en este plano se puede clasificar el origen de coordenadas en el
plano de fase.
CAMPUS TECNOLÓGICO DE LA UNIVERSIDAD DE NAVARRA. NAFARROAKO UNIBERTSITATEKO CAMPUS TEKNOLOGIKOA
Paseo de Manuel Lardizábal 13. 20018 Donostia-San Sebastián. Tel.: 943 219 877 Fax: 943 311 442 www.esi.unav.es [email protected]