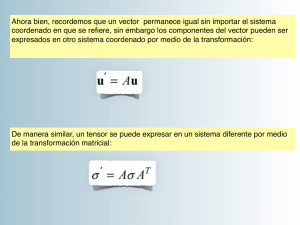
1 Tensores

1 Tensores
1
Tensores
1.1 Introducción
Muchos fenómenos físicos se representan matemáticamente mediante Tensores, los cuales,
por necesidad son representados en un sistema de referencia, de este modo surge el
concepto de componentes del tensor. Si bien los tensores son independientes del sistema
de referencia, las componentes serán dependientes y variarán con éste.
Los tensores pueden ser clasificados según su orden como:
Escalar (Tensor de orden 0): Cantidad que tiene magnitud pero no dirección (ejemplo:
densidad de masa, temperatura, presión). Los escalares pueden ser funciones del espacio y
del tiempo y no necesariamente han de ser constantes.
Vector (Tensor de orden 1): Cantidad que tiene magnitud y dirección (ejemplo: velocidad,
aceleración, fuerza). Será simbolizado por una letra en negrita con una flecha en la parte
r
superior del tensor, i.e.: • .
Tensor de segundo orden (Tensor de orden 2): Cantidad que tiene magnitud y dos
direcciones (ejemplo: tensión, deformación). Será simbolizado por una letra en negrita.
Para los tensores de órdenes superiores también usaremos letras en negrita.
Este capítulo trata del estudio detallado de los tensores (escalar, vector, tensor de segundo
orden, y de orden superior), y de algunas herramientas matemáticas que darán soporte al
desarrollo de las teorías que se exponen en los capítulos posteriores.
Primeramente, revisaremos algunas operaciones de vectores independientemente del
sistema de coordenadas. A continuación, introduciremos el sistema de coordenadas
rectangulares para expresar las componentes de un vector en dicho sistema. Una vez
definido el sistema de referencia, podremos expresar las operaciones con vectores tan sólo
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
12
en función de sus componentes. Por último, expondremos la notación indicial por su
simplicidad y fácil manipulación matemática.
Posteriormente estudiaremos los tensores de orden superior, poniendo especial énfasis en
los tensores de segundo orden. Para finalizar, plantearemos los campos de tensiones y los
sistemas de coordenadas cilíndricas y esféricas.
1.2 Vectores
A continuación presentamos algunas operaciones entre vectores en el espacio vectorial
tridimensional Euclidiano (E ) .
r
r
Suma: Sean los vectores a y b pertenecientes al espacio de vectores. La suma de los
r
mismos, ver Figura 1.1(a), será otro vector ( c ) dado por:
r r r r r
c =a+b=b+ a
r
a
(1.1)
r
d
r
c
r
−b
r
b
r
a
r
c
r
b
a)
b)
Figura 1.1: Suma y resta de vectores.
r
r r
Resta: La resta de dos vectores ( a , b ), ver Figura 1.1(b), será otro vector ( d ) dado por:
r r r
d=a−b
(1.2)
r r r r r
r r
r r
(a + b) + c = a + (b + c ) = a + b + c
(1.3)
r r r
Para los vectores a , b y c , pertenecientes al espacio de vectores, se cumplen las siguientes
relaciones:
r
r
Producto por un escalar λ : Sea el vector a , el producto λa será un vector con la misma
r
dirección de a , mientras que su módulo y sentido dependerán del valor del escalar λ , tal y
como se indica en la Figura 1.2.
Producto Escalar
r
r
Sean los vectores a y b , se define el Producto Escalar de ambos vectores como un escalar γ
de valor:
r r
r r
γ = a ⋅ b = a b cos θ
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.4)
Por: Eduardo W.V. Chaves
1 TENSORES
13
siendo θ el ángulo formado por los dos vectores, y • es el módulo (o magnitud) de • , ver
r r
r r
Figura 1.3(a). Podemos concluir también que a ⋅ b = b ⋅ a .
r
r
Para el caso en que a = b obtenemos que:
r r r r
r r r r
r
r r
=0 º
a ⋅ a = a a cos θ θ
→ a ⋅ a = a a ⇒ a = a ⋅ a
λ =1
λ >1
r
a
0 < λ <1
λ<0
r
λa
r
a
(1.5)
r
a
r
a
r
λa
r
λa
Figura 1.2: Producto de un vector por un escalar.
Vector Unitario (versor)
r
Dado un vector a , el versor (vector unitario) asociado a esta dirección será un vector â
r
con la misma dirección y sentido de a , definido por:
r
a
aˆ = r
a
(1.6)
r
r
donde a es el módulo del vector a . Si â es un vector unitario, entonces debe cumplir
que:
aˆ = 1
(1.7)
r
0
(1.8)
Vector Nulo
El vector nulo viene representado por:
Vector Proyección
r
r
El vector proyección del vector a sobre el vector b (Figura 1.3(b)) será un vector con la
r
r
dirección de b y con módulo de valor projbr a dado por:
r r
projbr a = a ⋅ bˆ
r
donde b̂ es el versor según la dirección de b , luego se cumple que:
r r
r a ⋅b
projbr a = r
b
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.9)
(1.10)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
14
0≤θ≤π
r
a
θ
r
a
.
θ
r
b
r
projbr a
a)
r
b
b)
Figura 1.3: Producto escalar.
r
r
Podemos obtener el vector projbr a como su módulo projbr a multiplicado por el versor
r
según la dirección de b :
r r
r a⋅b
proj a = r
b
r
b
r
r r
b
a⋅b r
r = r r b
b
b b
1
424
3
(1.11)
escalar
Ortogonalidad de dos vectores:
Dos vectores son ortogonales entre sí cuando se cumple la siguiente condición:
r r
a⋅b = 0
(1.12)
Producto Vectorial
r
r
r
El producto vectorial de dos vectores a y b da como resultado un tercer vector c que se
caracteriza por ser perpendicular a estos dos vectores (Figura 1.4), y que posee las
siguientes características:
ƒ
ƒ
ƒ
Representación:
r r
r r r
c = a ∧ b = −b ∧ a
r
r
r
Dado que c es perpendicular a a y a b , se cumple entonces que:
r r r r
a⋅c = b ⋅c = 0
r
El módulo de c es por definición:
r
r r
c = a b sin θ
r
(1.13)
(1.14)
(1.15)
r
siendo θ el menor ángulo formado entre los vectores a y b , ver Figura 1.4.
El módulo del producto vectorial es el área ( A ) del paralelogramo formado por estos dos
vectores, ver Figura 1.4(a):
r r
A= a∧b
(1.16)
y como consecuencia el área del triangulo formado por los puntos OCD (Figura 1.4(b))
será:
AT =
1 r r
a∧b
2
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.17)
Por: Eduardo W.V. Chaves
1 TENSORES
15
r
r
r
r
Si a y b son colineales (linealmente dependiente, i.e. a = αb , donde α es un escalar), el
r
producto vectorial entre ellos resultará el vector nulo, 0 .
r r r
c = a∧b
D
r
b
..
r
c
A
θ
r
a
O
r
b
θ
.
O .
C
D
AT
r
a
C
r r r
−c =b∧a
a)
b)
Figura 1.4: Producto vectorial.
Triple Producto Escalar
r r r
Dados tres vectores ( a, b, c ) se denomina el triple producto escalar a:
(
)
( )
(
)
r r r r r r r r r
a ⋅ b ∧ c = b ⋅ (c ∧ a) = c ⋅ a ∧ b = V
r r r
r r r
r r r
V = −a ⋅ c ∧ b = −b ⋅ (a ∧ c ) = −c ⋅ b ∧ a
(
)
(1.18)
El resultado de esta operación es el volumen del paralelepípedo ( V ) formado por estos tres
vectores, tal y como se muestra en la Figura 1.5.
r
r
Luego, para vectores cualesquiera a , b se cumple que:
(
)
r r r r
a⋅ b ∧ a = 0
r r
r
r
(1.19)
Dados los vectores a , b , c , d , y α , β escalares, la siguiente propiedad es válida:
r r r
r r r
r
r r r
(α a + β b) ⋅ (c ∧ d) = α a ⋅ (c ∧ d) + β b ⋅ (c ∧ d)
(1.20)
NOTA: Algunos autores representan el triple producto escalar por la siguiente
r r r r r r
r r r r r r
r r r r r r
nomenclatura, [a, b, c ] ≡ a ⋅ b ∧ c , [b, c, a] ≡ b ⋅ (c ∧ a) , [c, a, b] ≡ c ⋅ a ∧ b , y así
sucesivamente. ■
(
)
(
)
V ≡ Triple producto escalar
r
r
a∧b
r
c
..
r
b
θ
V
r
a
Figura 1.5: Triple producto escalar.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
16
Triple Producto Vectorial
r
r
r
r
Dados tres vectores a , b y c , el triple producto vectorial resulta un vector w dado por
r r r r
w = a ∧ b ∧ c , siendo válidas las siguientes relaciones:
(
)
(
)
(
)
(
)
( )
r r r r r r
r r r r r r
r r r r
(1.21)
w = a ∧ b ∧ c = −c ∧ a ∧ b = c ∧ b ∧ a = (a ⋅ c ) b − a ⋅ b c
r
Observemos que el vector w es un vector contenido en el plano Π1 , formado por los vectores
r r
b y c , según se muestra en la Figura 1.6.
r r
Π1 - plano formado por b y c
Π1
Π2
r r r
Π 2 - plano formado por a y b ∧ c
r
c
r
b
r
w contenido en el plano Π1
r
a
r r
b∧c
r
w
Figura 1.6: Triple producto vectorial.
r
r
Ejemplo 1.1: Probar que si a y b son vectores se cumple que:
(ar ∧ br )⋅ (ar ∧ br ) = (ar ⋅ ar )(br ⋅ br ) − (ar ⋅ br )
2
Solución:
(ar ∧ br )⋅ (ar ∧ br )
(
)
2
r r 2
r r
r 2 r 2
= a ∧ b = a b sin θ = a b sin 2 θ
r 2 r 2
r 2 r 2
r 2 r 2
= a b 1 − cos 2 θ = a b − a b cos 2 θ
2
r 2 r 2
r r
r 2 r 2 r r 2
= a b − a b cos θ = a b − a ⋅ b
r r r r
r r 2
= (a ⋅ a) b ⋅ b − a ⋅ b
r r r 2 r r r 2
donde hemos considerado que a ⋅ a = a y b ⋅ b = b .
(
(
)
( ) ( )
)
( )
Transformación Lineal
Decimos que una transformación F es una transformación lineal cuando dados dos
r
r
vectores u y v y un escalar α se cumplen que:
ƒ
ƒ
r r
r
r
F (u + v ) = F (u) + F ( v )
r
r
F (αu) = αF (u)
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
17
1
2
Ejemplo 1.2: Verificar si para las siguientes transformaciones σ(ε) = Eε y ψ(ε) = Eε 2
son transformaciones lineales.
Solución: σ(ε1 + ε 2 ) = E [ε1 + ε 2 ] = Eε1 + Eε 2 = σ(ε1 ) + σ(ε 2 ) (transformación lineal)
σ( ε)
σ (ε 1 + ε 2 ) = σ (ε 1 ) + σ ( ε 2 )
σ (ε 2 )
σ (ε 1 )
ε1
ε2
ε
ε1 + ε 2
1
2
1
1
1
1
1
ψ(ε1 + ε 2 ) = E [ε1 + ε 2 ]2 = E ε12 + 2ε1ε 2 + ε 22 = Eε12 + Eε 22 + E 2ε1ε 2
lineal ya que:
2
2
2
2
2
= ψ ( ε 1 ) + ψ ( ε 2 ) + Eε 1 ε 2 ≠ ψ ( ε 1 ) + ψ ( ε 2 )
La transformación ψ(ε) = Eε 2 se demuestra fácilmente que no es una transformación
[
]
ψ ( ε)
ψ (ε1 + ε 2 )
ψ (ε1 ) + ψ (ε 2 )
ψ (ε 2 )
ψ (ε1 )
ε1
ε2
ε1 + ε 2
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
ε
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
18
1.3 Sistema de Coordenadas
Un tensor es una interpretación matemática de un concepto físico. Sus componentes
adoptan valores que dependen del sistema de coordenadas elegido para representarlo, ver
Figura 1.7.
TENSORES
Interpretación matemática de conceptos físicos
(Independiente del sistema de coordenadas)
COMPONENTES
Representación del Tensor en
un Sistema de Coordenadas
Figura 1.7: Esquema tensor-componentes.
r
Consideremos un tensor de orden uno ( a ) como el representado en la Figura 1.8(a), la
representación de este tensor en un sistema de coordenadas genérico ( ξ1 , ξ 2 , ξ 3 ) se hace a
través de sus componentes ( a1 , a 2 , a 3 ), ver Figura 1.8(b).
ξ3
ξ2
r
a ( a1 , a 2 , a 3 )
r
a
r
a
b)
a)
ξ1
Figura 1.8: Representación de un vector.
Los sistemas de coordenadas pueden ser de varios tipos: coordenadas curvilíneas,
coordenadas cartesianas rectangulares, coordenadas cilíndricas y coordenadas esféricas,
entre otros.
1.3.1
Sistema de Coordenadas Rectangulares
El sistema de coordenadas cartesianas rectangulares viene definido por tres vectores: î , ĵ ,
k̂ , los cuales constituyen una base ortonormal. Se entiende por base ortonormal, aquella que
satisface las siguientes propiedades:
1. Los vectores que forman esta base son unitarios (versores):
ˆi = ˆj = kˆ = 1
(1.22)
o lo que es igual:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
19
ˆi ⋅ ˆi = ˆj ⋅ ˆj = kˆ ⋅ kˆ = 1
(1.23)
2. Los vectores de esta base son ortogonales entre sí, es decir:
ˆi ⋅ ˆj = ˆj ⋅ kˆ = kˆ ⋅ ˆi = 0
(1.24)
3. El producto vectorial entre los versores que forman esta base cumple lo siguiente:
ˆi ∧ ˆj = kˆ
ˆj ∧ kˆ = ˆi
;
;
kˆ ∧ ˆi = ˆj
(1.25)
Para conocer el sentido del vector resultante del producto vectorial utilizamos la regla de la
mano derecha, tal y como se indica en la Figura 1.9.
ˆj ∧ kˆ = ˆi
ˆi ∧ ˆj = kˆ
ĵ
kˆ ∧ ˆi = ˆj
ĵ
ĵ
î
î
î
k̂
k̂
k̂
(1.26)
Figura 1.9: Regla de la mano derecha.
1.3.2
Representación de los Vectores en el Sistema de
Coordenadas Cartesianas
r
En el sistema de coordenadas cartesianas, el vector a (Figura 1.10) está representado por
sus componentes ( a x , a y , a z ) como:
r
a = a x ˆi + a y ˆj + a z kˆ
(1.27)
y
ay
ĵ
k̂
r
a
î
ax
x
az
z
Figura 1.10: Vector en el sistema cartesiano.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
20
Las operaciones básicas particularizadas a este sistema de referencia son:
ƒ
r
r
Producto Escalar de dos vectores a y b
r r
a ⋅ b = (a x ˆi + a y ˆj + a z kˆ ) ⋅ (b x ˆi + b y ˆj + b z kˆ ) = (a x b x + a y b y + a z b z )
r r
(1.28)
r
Luego, se cumple que a ⋅ a = a x a x + a y a y + a z a z = a 2x + a 2y + a 2z = a
2
NOTA: La proyección de un vector sobre una dirección determinada obtenemos a
través del producto escalar del vector y del versor que define esa dirección. Como
r
ejemplo, si quisiéramos obtener la componente del vector a según la dirección y
r
(representado por su versor ĵ ) es suficiente con: a ⋅ ˆj = (a x ˆi + a y ˆj + a z kˆ ) ⋅ (ˆj) = a y .■
ƒ
r
módulo del vector a
r
a = a 2x + a 2y + a 2z
ƒ
r
vector unitario correspondiente al vector a
r
ax
a
ˆi +
aˆ = r =
2
2
2
a
ax + a y + az
ƒ
ƒ
ay
a 2x
+
a 2y
+
a 2z
ˆj +
az
a 2x
+
a 2y
+
a 2z
kˆ
(1.30)
vector nulo
r
0 = 0 ˆi + 0 ˆj + 0 kˆ
r
r
Suma de dos vectores a y b
r r
a + b = (a x ˆi + a y ˆj + a z kˆ ) + (b x ˆi + b y ˆj + b z kˆ )
= (a + b ) ˆi + a + b ˆj + (a + b ) kˆ
x
ƒ
(1.29)
(
x
y
y
)
z
(1.31)
(1.32)
z
r
r
Resta de dos vectores a y b
r r
a − b = (a x ˆi + a y ˆj + a z kˆ ) − (b x ˆi + b y ˆj + b z kˆ )
= (a − b ) ˆi + a − b ˆj + (a − b ) kˆ
x
x
(
y
y
)
ƒ
Multiplicación por un escalar λ
ƒ
r
λa = λa x ˆi + λa y ˆj + λa z kˆ
r
r
Producto Vectorial de dos vectores a y b
ˆi
r r r
c = a ∧ b = ax
z
(1.33)
z
(1.34)
ˆj
ay
kˆ
a y az
a ay
ˆi − a x a z ˆj + x
kˆ
az =
by bz
bx b y
bx bz
bx b y bz
= (a y b z − a z b y )ˆi − (a xb z − a z b x )ˆj + (a xb y − a y b x )kˆ
(1.35)
donde el símbolo • ≡ det (•) se emplea para indicar el determinante de una matriz.
ƒ
r r r
Triple Producto Escalar de los vectores [ a, b, c ] en términos de sus
componentes viene definido por:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
21
ax
r r r
r r r r r r r r r
V (a, b, c ) = a ⋅ b ∧ c = b ⋅ (c ∧ a) = c ⋅ a ∧ b = b x
cx
by bz
bx by
bx bz
= ax
− ay
+ az
cy cz
cx cy
cx cz
(
)
(
(
ƒ
)
)
ay
az
by
cy
bz
cz
(1.36)
(
)
= a x b y c z − b z c y − a y (b x c z − b z c x ) + a z b x c y − b y c x
r r r
Triple Producto Vectorial de los vectores ( a, b, c ) en función de sus
componentes es:
(
r r r
a∧ b∧c
)
( )
r r r r r r
= (a ⋅ c ) b − a ⋅ b c
= (λ 1b x − λ 2 c x ) ˆi + λ 1b y − λ 2 c y ˆj + (λ 1b z − λ 2 c z ) kˆ
r r
r r
con λ 1 = a ⋅ c = a x c x + a y c y + a z c z , y λ 2 = a ⋅ b = a x b x + a y b y + a z b z .
(
)
(1.37)
Ejemplo 1.3: Considérense los puntos A(1,3,1) , B (2,−1,1) , C (0,1,3) y D(1,2,4 ) .
Se pide:
→
→
1) Encontrar el área del paralelogramo definido por AB y AC ;
→
→
→
2) Encontrar el volumen del paralelepípedo definido por: AB , AC y AD ;
→
→
3) Encontrar el vector proyección del vector AB sobre el vector BC .
Solución:
→
→
1) Primero se calculan los vectores AB y AC :
→
→
→
r
a = AB = OB − OA =
r
→
→
→
b = AC = OC − OA =
(2ˆi − 1ˆj + 1kˆ ) − (1ˆi + 3ˆj + 1kˆ ) = 1ˆi − 4ˆj + 0kˆ
(0ˆi + 1ˆj + 3kˆ )− (1ˆi + 3ˆj + 1kˆ ) = −1ˆi − 2ˆj + 2kˆ
Utilizando la definición (1.35) se obtiene el producto vectorial:
ˆi
r r
a∧b= 1
ˆj kˆ
− 4 0 = ( −8)ˆi − 2ˆj + ( −6)kˆ
−1 − 2
2
El área del paralelogramo será igual al módulo del vector resultante del producto
vectorial:
r r
A = a ∧ b = (−8) 2 + (−2) 2 + ( −6) 2 = 104 (unidades cuadradas)
→
2) Calculando el vector AD :
(
) (
)
→
→
→
r
c = AD = OD − OA = 1ˆi + 2ˆj + 4kˆ − 1ˆi + 3ˆj + 1kˆ = 0ˆi − 1ˆj + 3kˆ
Utilizando la definición (1.36) obtenemos que:
(
r r r
r r r
V (a, b, c ) = c ⋅ a ∧ b
)
=
(0ˆi − 1ˆj + 3kˆ )⋅ (− 8ˆi − 2ˆj − 6kˆ )
= 0 + 2 − 18 = 16 (unidades cúbicas)
→
3) A continuación calculamos el vector BC :
(
) (
)
→
→
→
BC = OC − OB = 0ˆi + 1ˆj + 3kˆ − 2ˆi − 1ˆj + 1kˆ = −2ˆi + 2ˆj + 2kˆ
Utilizando la ecuación (1.11):
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
22
proj
→
→
BC
→
AB =
→
BC ⋅ AB
→
→
BC
BC
⋅4
1
42
3
→
BC
→
BC
(− 2ˆi + 2ˆj + 2kˆ )⋅ (1ˆi − 4ˆj + 0kˆ ) (− 2ˆi + 2ˆj + 2kˆ )
(− 2ˆi + 2ˆj + 2kˆ )⋅ (− 2ˆi + 2ˆj + 2kˆ )
=
2
=
(− 2 − 8 + 0 ) (− 2ˆi + 2ˆj + 2kˆ )
(4 + 4 + 4 )
proj
1.3.3
→
→
BC
AB =
5ˆ 5ˆ 5 ˆ
i − j− k
3
3
3
Convenio de Suma de Einstein
r
Definimos en la expresión (1.27) la representación de un vector a en el sistema de
coordenadas rectangular:
r
a = a x ˆi + a y ˆj + a z kˆ
(1.38)
Podemos reescribir la representación anterior como:
r
a = a1eˆ 1 + a 2 eˆ 2 + a 3 eˆ 3
(1.39)
donde hemos considerado que: a1 ≡ a x , a 2 ≡ a y , a 3 ≡ a z , eˆ 1 ≡ î , eˆ 2 ≡ ĵ , eˆ 3 ≡ k̂ , tal y
como se indica en la Figura 1.11.
y
a y ≡ a2
r
a
ˆj ≡ eˆ
2
a z ≡ a3
ˆi ≡ eˆ
1
a x ≡ a1
x
kˆ ≡ eˆ 3
z
Figura 1.11: Vector en el sistema cartesiano.
De esta forma podemos expresar la representación simbólica del vector (1.39) como una
suma:
r
a = a1eˆ 1 + a 2 eˆ 2 + a 3 eˆ 3 =
3
∑ a eˆ
i
i
(1.40)
i =1
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
23
o simplemente utilizando el convenio de suma o Notación de Einstein, según la cual, se
utilizan índices repetidos para indicar suma, así pues la expresión (1.40) queda de la
siguiente manera:
r
a = a1eˆ 1 + a 2 eˆ 2 + a 3 eˆ 3 = a i eˆ i
(i = 1,2,3)
r
a = a i eˆ i
(i = 1,2,3)
(1.41)
NOTA: La notación de suma fue introducida por Albert Einstein en 1916, dando origen
así a la notación indicial. ■
1.4 Notación Indicial
Utilizando notación indicial los ejes del sistema de coordenadas son designados por la letra
x con un subíndice. Por eso xi no representa un único valor, sino i valores, es decir x1 ,
x 2 , x3 ( si i = 1,2,3 ) donde estos valores ( x1 , x 2 , x3 ) corresponden respectivamente a los
ejes ( x , y , z ).
r
En un sistema de coordenadas cartesianas, un vector a será representado por sus
componentes en la base del citado sistema de la siguiente forma:
r
a = a1eˆ 1 + a 2 eˆ 2 + a 3 eˆ 3
(1.42)
donde ê1 , ê 2 , ê 3 son versores (vectores unitarios), tal y como se muestra en la Figura
1.12, y a1 , a 2 , a 3 son las componentes del vector. En notación indicial las componentes del
vector serán representadas por a i . Si no se indica el rango del subíndice, se supondrá que
adopta los valores 1,2,3. Por tanto, las componentes de vector pueden representarse de la
siguiente forma:
 a1 
r
(a) i = a i = a 2 
 a 3 
(1.43)
y ≡ x2
a2
r
a
ê 2
a3
ê1
a1
ê 3
x ≡ x1
z ≡ x3
Figura 1.12: Vector en el sistema cartesiano.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
24
r
Componentes del Vector Unitario: Dado un vector a , el vector unitario asociado a esta
dirección será un vector â dado por:
r
ˆa = a
r
a
aˆ = 1
con
(1.44)
cuyas componentes serán:
aˆ i =
ai
a12
+
a 22
+
a 32
=
ai
a ja j
=
ai
ak ak
(i, j , k = 1,2,3)
(1.45)
Los subíndices se denominan de 2 formas:
Subíndices libres aquellos que sólo aparecen una vez en un término de la expresión. En la
ecuación anterior el subíndice libre es el subíndice ( i ). El número de
subíndices libres indica el orden del tensor.
Subíndices mudos son los subíndices que se repiten en una expresión indicando suma. En la
ecuación anterior (1.45) son, o bien el ( j ), o bien el ( k ).
OBS.: Un subíndice en un término de una expresión sólo puede aparecer una o
dos veces. En el caso de que aparezca tres o más veces, entonces la expresión es
incorrecta.
Producto Escalar: Utilizando las definiciones (1.4) y (1.28), podemos expresar el producto
escalar en notación indicial de la siguiente forma:
r r
r r
γ = a ⋅ b = a b cos θ
γ = a1b1 + a 2 b 2 + a 3b 3 = a i b i = a j b j
(1.46)
(i, j = 1,2,3)
Ejemplo 1.4: Reescribir en notación indicial las siguientes expresiones:
1) a1 x1 x 3 + a 2 x 2 x 3 + a 3 x 3 x 3
Solución:
a i xi x 3
(i = 1,2,3)
2) x1 x1 + x2 x2
Solución:
xi x i
(i = 1,2)
 a11 x + a12 y + a13 z = b x

3) a 21 x + a 22 y + a 23 z = b y

 a 31 x + a 32 y + a 33 z = b z
Solución:
 a11 x1 + a12 x 2 + a13 x 3 = b1

a 21 x1 + a 22 x 2 + a 23 x 3 = b2
a x + a x + a x = b
32 2
33 3
3
 31 1
 a1 j x j = b1

 → a 2 j x j = b2

 a 3 j x j = b3
índice
mudo j
índice
libre
i →
a ij x j = bi
Como podemos apreciar, la utilización de la notación indicial supone que la expresión
quede muy concisa. En muchos casos, tratar de realizar manipulaciones algebraicas sin
utilizar notación indicial o tensorial es casi imposible debido a la gran cantidad de términos
que pueden intervenir.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
25
Ejemplo 1.5: Expandir la expresión: Aij x i x j
(i, j = 1,2,3)
Solución: Los índices i, j son índices mudos (indican suma), no hay índice libre, y como
resultado tenemos un escalar. Expandimos primero el índice mudo i y a continuación el
índice j , resultando así:
expandiendo j
oi
  
→ A1 j x1 x j + A2 j x 2 x j + A3 j x 3 x j
Aij x i x j expandiend
1
424
3 1
424
3 1
424
3
A11 x1 x1 A21 x 2 x1 A31 x 3 x1
+
+
+
A12 x1 x 2
A22 x 2 x 2
A32 x 3 x 2
+
+
+
A13 x1 x 3
A23 x 2 x 3
A33 x 3 x 3
Reagrupando los términos anteriores obtenemos:
Aij x i x j = A11 x1 x1 + A12 x1 x 2 + A13 x1 x 3 + A21 x 2 x1 + A22 x 2 x 2 +
A23 x 2 x 3 + A31 x 3 x1 + A32 x 3 x 2 + A33 x 3 x 3
1.4.1
Delta de Kronecker
El símbolo delta de Kronecker δ ij definimos de la manera siguiente:
 1 si i = j

δ ij = 
 0 si i ≠ j

(1.47)
Observemos también que el producto escalar de la base ortonormal eˆ i ⋅ eˆ j es 1 si i = j y 0
si i ≠ j . Si lo anterior lo exponemos de forma explícita, obtendremos:
 eˆ 1 ⋅ eˆ 1

eˆ i ⋅ eˆ j = eˆ 2 ⋅ eˆ 1
eˆ 3 ⋅ eˆ 1

eˆ 1 ⋅ eˆ 2
eˆ 2 ⋅ eˆ 2
eˆ 3 ⋅ eˆ 2
eˆ 1 ⋅ eˆ 3  1 0 0

eˆ 2 ⋅ eˆ 3  = 0 1 0 = δ ij
eˆ 3 ⋅ eˆ 3  0 0 1
(1.48)
Una propiedad muy interesante de la delta de Kronecker la demostramos a continuación
r
con el siguiente ejemplo, sea un vector ( V ) de componentes ( Vi ) se cumple:
δ ij Vi = δ 1 jV1 + δ 2 jV2 + δ 3 jV3
(1.49)
luego, como ( j = 1,2,3) es un índice libre tenemos:
j = 1 ⇒ δ ij Vi = δ 11V1 + δ 21V2 + δ 31V3 = V1 

j = 2 ⇒ δ ij Vi = δ 12V1 + δ 22V2 + δ 32V3 = V 2  ⇒ δ ij Vi = V j

j = 3 ⇒ δ ijVi = δ 13V1 + δ 23V 2 + δ 33V3 = V3 
(1.50)
Es decir, en la presencia del símbolo Delta de Kronecker reemplazamos el índice repetido,
tal y como se indica a continuación:
δi
j
V
i
=V j
(1.51)
Por esta razón, la delta de Kronecker es frecuentemente llamada operador de sustitución.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
26
Otros ejemplos relacionados con este operador se presentan a continuación:
δ ij Aik = A jk , δ ij δ ji = δ ii = δ jj = δ 11 + δ 22 + δ 33 = 3 , δ ji a ji = aii = a jj = a11 + a 22 + a 33
También podemos verificar que se cumple que:
 ∂x1

 ∂x1
∂xi  ∂x 2
=
∂x j  ∂x1

 ∂x 3
 ∂x1
∂x1
∂x 2
∂x 2
∂x 2
∂x3
∂x 2
∂x1 

∂x 3  1 0 0
∂x 2  
= 0 1 0 = δ ij

∂x 3
 

∂x 3  0 0 1 
∂x 3 
(1.52)
r
Sea la base ortonormal ê i , podemos obtener las componentes del vector a en esta base
como:
r
a ⋅ eˆ i = a p eˆ p ⋅ eˆ i = a p δ pi = a i
(1.53)
Con eso, también podemos representar un vector como:
r
r
a = a i eˆ i = (a ⋅ eˆ i )eˆ i
(1.54)
Ejemplo 1.6: Resolver las siguientes expresiones:
1) δ ii δ jj
Solución:
δ ii δ jj = (δ 11 + δ 22 + δ 33 )(δ 11 + δ 22 + δ 33 ) = 3 × 3 = 9
2) δ α1δ αγ δ γ1
Solución:
δ α1δ αγ δ γ1 = δ γ1δ γ1 = δ 11 = 1
NOTA: Observar que es incorrecto hacer la siguiente operación δ γ1δ γ1 ≠ δ γγ = 3 ≠ δ 11 = 1 ,
ya que lo que se reemplaza es el índice repetido ■
1.4.2
Símbolo de Permutación
El símbolo de permutación  ijk viene definido como:
 ijk
+ 1 si (i, j , k ) ∈ {(1,2,3), (2,3,1), (3,1,2)}

= − 1 si (i, j , k ) ∈ {(1,3,2), (3,2,1), (2,1,3)}
0 para el resto de casos i.e. : si (i = j ) o ( j = k ) o (i = k )

(1.55)
NOTA:  ijk son las componentes del pseudo-tensor Levi-Civita, que será definido mas
adelante. ■
Otra forma de expresar este operador es a través de sus subíndices:
1
2
 ijk = (i − j )( j − k )(k − i )
(1.56)
Los valores de  ijk pueden ser fácilmente memorizados si utilizamos la Figura 1.13(a), en el
cual si los valores de los índices están ordenados en el sentido horario el valor de  ijk es
igual a 1 y si están ordenados en el sentido antihorario  ijk asumirá el valor − 1 .
Con la definición (1.67) y utilizando la Figura 1.13(b) podemos comprobar que las
siguientes relaciones son válidas:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
27
 ijk =  jki =  kij
(1.57)
 ijk = − ikj = − jik = − kji
(ijk ) = 1
1
i
(ijk ) = −1
3
ijk =  jki = kij
 ijk = − ikj
ijk = −ikj
2
k
j
= − kji
= − jik
b)
a)
Figura 1.13: Símbolo de permutación.
Si expresamos el símbolo de permutación en función de la delta de Kronecker (operador de
sustitución), obtenemos:
 ijk
=  lmn δ li δ mj δ nk
= δ 1i δ 2 j δ 3k − δ 1i δ 3 j δ 2 k − δ 2i δ 1 j δ 3k + δ 3i δ 1 j δ 2 k + δ 2i δ 3 j δ 1k − δ 3i δ 2 j δ 1k
= δ 1i δ 2 j δ 3k − δ 3 j δ 2 k − δ 1 j (δ 2i δ 3k − δ 3i δ 2 k ) + δ 1k δ 2i δ 3 j − δ 3i δ 2 j
(
)
(
(1.58)
)
lo que es igual al resultado del siguiente determinante:
 ijk
δ 1i δ 1 j δ 1k δ 1i δ 2i δ 3i
= δ 2i δ 2 j δ 2 k = δ 1 j δ 2 j δ 3 j
δ 3i δ 3 j δ 3k δ 1k δ 2 k δ 3k
(1.59)
Por lo tanto podemos expresar el producto  ijk  pqr como el producto de dos
determinantes que definimos a continuación:
Si
tenemos en
 ijk  pqr
δ 1i
= δ1 j
δ 1k
δ 2i δ 3i δ 1 p δ 1q δ 1r
δ 2 j δ 3 j δ 2 p δ 2q δ 2r
δ 2 k δ 3k δ 3 p δ 3q δ 3r
cuenta
que
dadas dos matrices cuadradas se
(1.60)
cumple
que
det (AB ) = det (A )det (B ) , donde det (•) ≡ • es el determinante de la matriz • , la relación
(1.60) resulta ser:
 ijk  pqr
 δ 1i
= δ 1 j
δ 1k
δ 2i
δ2j
δ 2k
δ 3i   δ 1 p δ 1q δ 1r 


δ 3 j  δ 2 p δ 2 q δ 2 r  ⇒
δ 3k  δ 3 p δ 3q δ 3r 
 ijk  pqr
δ ip δ iq δ ir
= δ jp δ jq δ jr
δ kp δ kq δ kr
(1.61)
Observemos que el término δ ip fue obtenido a través de la operación:
δ 1i δ 1 p + δ 2i δ 2 p + δ 3i δ 3 p = δ mi δ mp = δ ip , análogamente podemos obtener el resto de
términos. Para el caso particular en el que r = k la relación (1.61) puede expresarse como:
 ijk  pqk = δ ip δ jq − δ iq δ jp
i, j , k , p, q = 1,2,3
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.62)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
28
Ejemplo 1.7: a) Probar que  ijk  pjk = 2δ ip y que  ijk  ijk = 6 . b) Obtener el valor numérico
de la siguiente expresión  ijk δ 2 j δ 3k δ 1i .
Solución: a) Utilizando la expresión (1.62),  ijk  pqk = δ ip δ jq − δ iq δ jp , y haciendo q = j ,
resulta:
 ijk  pjk = δ ip δ jj − δ ij δ jp
= δ ip 3 − δ ip = 2δ ip
Partiendo del resultado anterior, es trivial la siguiente comprobación:
 ijk  ijk = 2δ ii = 6
b)  ijk δ 2 j δ 3k δ 1i = 123 = 1
ƒ
r
r
r
El Producto Vectorial de dos vectores a y b resultará un vector c , definido en
(1.35), y viene dado por:
eˆ 1
r r r
c = a ∧ b = a1
eˆ 2
a2
b1
b2
eˆ 3
a 3 = (a 2 b 3 − a 3b 2 )eˆ 1 + (a 3b1 − a1b 3 )eˆ 2 + (a1b 2 − a 2 b1 )eˆ 3
14243
142
4 43
4
14243
c3
c1
c2
b3
(1.63)
Podemos utilizar la definición del símbolo de permutación  ijk , definido en (1.55), y
r
expresar las componentes de c como:
c 1 = 123 a 2 b 3 + 132 a 3b 2 = 1 jk a j b k 

c 2 =  231a 3b1 +  213 a1b 3 =  2 jk a j b k  ⇒ c i =  ijk a j b k
(1.64)

c 3 =  312 a1b 2 +  321a 2 b1 =  3 jk a j b k 
r r
Luego, el producto vectorial, entre dos vectores a , b , podrá ser representado a través del
símbolo de permutación como:
r r
a ∧ b =  ijk a j b k eˆ i
a j eˆ j ∧ b k eˆ k = a j b k  ijk eˆ i
(1.65)
a j b k (eˆ j ∧ eˆ k ) = a j b k  ijk eˆ i = a j b k  jki eˆ i
Con lo cual concluimos que:
(eˆ j ∧ eˆ k ) =  ijk eˆ i
(1.66)
También podemos relacionar el operador de permutación con la base ortonormal ê i a
través del triple producto escalar de dicha base:
(eˆ
)⋅ eˆ
=  ijm eˆ m ⋅ eˆ k =  ijm δ mk =  ijk
r r r
ƒ El Triple Producto Escalar de los vectores ( a, b, c ) viene dado por:
r r r
λ = a ⋅ b ∧ c = a i eˆ i ⋅ b j eˆ j ∧ c k eˆ k = a i b j c k eˆ i ⋅ eˆ j ∧ eˆ k =  ijk a i b j c k
r r r
λ = a ⋅ b ∧ c =  ijk a i b j c k
(i, j , k = 1,2,3)
eˆ i ∧ eˆ j =  ijm eˆ m
(
)
⇒
(
(
)
i
∧ eˆ j
)
k
(
)
(1.67)
(1.68)
(1.69)
ó
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
29
a1 a 2
r r r r r r r r r
λ = a ⋅ b ∧ c = b ⋅ (c ∧ a) = c ⋅ a ∧ b = b1 b 2
(
)
(
)
)
c2
(1.70)
c3
r r r r r r r r r
Demostraremos que se cumplen a ⋅ b ∧ c = b ⋅ (c ∧ a) = c ⋅ a ∧ b partiendo de la relación
(
c1
a3
b3
(
)
(1.69), y además teniendo en cuenta las relaciones dadas en (1.57), obtenemos que:
(
r r r r r r
[a, b, c] ≡ a ⋅ b ∧ c
)
= ijk aib j c k
r r r
r r r
=  jki aib j c k = b ⋅ (c ∧ a) ≡ [b, c, a]
r r r
r r r
=  kij aib j c k = c ⋅ a ∧ b ≡ [c, a, b]
r r r
r r r
= −ikj aib j c k = −a ⋅ c ∧ b ≡ −[a, c, b]
r r r
r r r
= − jik aib j c k = −b ⋅ (a ∧ c ) ≡ −[b, a, c ]
r r r
r r r
= − kji aib j c k = −c ⋅ b ∧ a ≡ −[c, b, a]
(
(
)
(
)
(1.71)
)
Observemos que:
a1 a 2
r r r
r r r
[a, b, c] = −[a, c, b] = b1 b 2
c1
c2
a1
a3
b 3 = − c1
c3
a2
c2
a3
c3
b1 b 2
b3
(1.72)
con lo cual hemos demostrado que si intercambiamos filas (o columnas) el signo del
determinante cambia.
(r r ) (r r )
Ejemplo 1.8: Escribir la siguiente relación a ∧ b ⋅ c ∧ d sin emplear el producto
vectorial.
r r
Solución: Observemos que el producto vectorial a ∧ b lo podemos expresar de la siguiente
(
(
)
)
r r
forma: a ∧ b = a j eˆ j ∧ b k eˆ k =  ijk a j b k eˆ i , cuyo resultado es un vector, donde hemos
utilizado la definición del símbolo de permutación (1.65). Análogamente podemos expresar
r r
r r
el producto vectorial c ∧ d como c ∧ d =  nlm c l d m eˆ n , por lo tanto:
(
(
)
r r
a∧b
(
)⋅ (
r r
c∧d
)
)
=  ijk a j b k eˆ i ) ⋅ ( nlm c l d m eˆ n )
=  ijk  nlm a j b k c l d m eˆ i ⋅ eˆ n
=  ijk  nlm a j b k c l d m δ in
=  ijk  ilm a j b k c l d m
Teniendo en cuenta que  ijk  ilm =  jki  lmi (relación (1.57)) y aplicando la relación (1.62),
i.e.:  jki  lmi = δ jl δ km − δ jm δ kl ) =  jki  ilm , concluimos que:
 ijk  ilm a j b k c l d m = (δ jl δ km − δ jm δ kl ) a j b k c l d m = a l b m c l d m − a m b l c l d m
(r r )
r r
Puesto que el subíndice mudo indica el producto escalar: a l c l = (a ⋅ c ) y b m d m = b ⋅ d ,
luego:
(ar ∧ br )⋅ (cr ∧ dr ) = (ar ⋅ cr ) (br ⋅ dr ) − (ar ⋅ dr )(br ⋅ cr )
r
r
r
r
Además, la expresión anterior se cumple para el caso cuando a = c y b = d , luego
(ar ∧ br )⋅ (ar ∧ br ) = ar ∧ br
2
( ) ( )( )
r r r r
r r r r
r
= (a ⋅ a) b ⋅ b − a ⋅ b b ⋅ a = a
2
r
b
2
( )
r r
− a⋅b
2
que es la misma expresión demostrada en el Ejemplo 1.1.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
30
(r r ) (r r ) r [r
r
r
] r [r
r
r
]
Ejemplo 1.9: Probar que: a ∧ b ∧ c ∧ d = c d ⋅ (a ∧ b) − d c ⋅ (a ∧ b)
Solución: Expresaremos en notación indicial los términos que están la derecha de la igualdad:
[
] [
]
r r r
rr r r
cr d ⋅ (a
∧ b) − d c ⋅ (a ∧ b)  = c p d i  ijk a j b k − d p c i  ijk a j b k


p
⇒  ijk a j b k c p d i −  ijk a j b k c i d p
⇒
 ijk a j b k c p d i − c i d p
[ (
)]
[ (
(
)]
)
Si utilizamos la propiedad de la delta de Kronecker:
⇒  ijk a j b k (δ pm c m d n δ ni − δ im c m d n δ np ) ⇒
( ijk a j b k ) c m d n (δ pm δ ni − δ im δ np )
y si consideramos (1.62), resulta: δ pm δ ni − δ im δ np =  pil  mnl . Reemplazamos en la expresión
anterior y obtenemos:
⇒ ( ijk a j b k ) c m d n ( pil  mnl ) ⇒
 pil [( ijk a j b k ) ( mnl c m d n )]
(r r )
(r r )
Dado que las componentes de a ∧ b son  ijk a j b k y las componentes de c ∧ d son
 mnl c m d n , obtenemos que:
[(r r ) (r r )]
 pil [( ijk a j b k ) ( mnl c m d n )] = a ∧ b ∧ c ∧ d
r
r
p
r
r
Ejemplo 1.10: Si a , b , c son vectores linealmente independientes y v un vector dado
por:
r
r
r r
r
v = αa + βb + γ c ≠ 0
Probar que los escalares α , β , γ vienen dados por:
 ijk v i b j c k
 ijk a i v j c k
 ijk a i b j v k
α=
; β=
; γ=
 pqr a p b q c r
 pqr a p b q c r
 pqr a p b q c r
r
r
r
Solución: Haciendo el producto escalar del vector v por el vector ( b ∧ c ) obtenemos que:
r r r
r r r
r r r
r r r
v ⋅ (b ∧ c ) = αa ⋅ (b ∧ c ) + β b ⋅ (b ∧ c ) + γ c ⋅ (b ∧ c )
14243
14243
=0
Obtenemos entonces el valor de α como:
=0
r r r
v ⋅ (b ∧ c )
α= r r r
a ⋅ (b ∧ c )
En componentes:
α=
v1
b1
v2
b2
v3
b3
c1
c2
c3
a1
b1
a2
b2
a3
b3
c1
c2
c3
=
v1
v2
b1
b2
c1
c2
v3
b3
c3
a1
a2
b1
b2
c1
c2
a3
b3
c3
=
 ijk v i b j c k
 pqr a p b q c r
Análogamente podemos obtener los parámetros β , γ , es decir, hacemos el producto
r
r
r
r
r
escalar del vector v por los vectores a ∧ c y a ∧ b , respectivamente.
Ejemplo 1.11: Probar la relación (1.37):
(
)
( )
r r r
r r r r r r
a ∧ b ∧ c = (a ⋅ c ) b − a ⋅ b c
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
31
(r r )
r
(r r )
Solución: Teniendo en cuenta que (d) i = b ∧ c i =  ijk b j c k y a ∧ d q =  qjk b j c k , podemos
obtener que:
[ar ∧ (br ∧ cr )]
q
=  qsi a s ( ijk b j c k ) =  qsi  ijk a s b j c k =  qsi  jki a s b j c k
= (δ qj δ sk − δ qk δ sj ) a s b j c k = δ qj δ sk a s b j c k − δ qk δ sj a s b j c k
( )
( )]
r r
r r
= a k b q c k − a j b j c q = b q (a ⋅ c ) − c q a ⋅ b
r r r rr r
r r r
⇒ a ∧ b ∧ c q = b(a ⋅ c ) − c a ⋅ b q
[ (
)] [
1.5 Operaciones Algebraicas con Tensores
1.5.1
Diádicas
El producto diádico de dos vectores (producto tensorial) resultará en un tensor de segundo
r
r
orden. Si consideramos los vectores v y u , el producto diádico vendrá representado por:
rr r r
uv ≡ u ⊗ v = A
(1.73)
donde el operador ⊗ denota el producto tensorial. Como veremos más adelante, cualquier
tensor puede ser representado a través de combinación lineal de productos diádicos
(diádicas). Verificaremos también que una diádica es un caso particular de un tensor de
segundo orden, Holzapfel(2000).
El producto diádico obedece a las siguientes leyes:
1.
r r r r r r
r
r r
(u ⊗ v ) ⋅ x = u( v ⋅ x ) ≡ u ⊗ ( v ⋅ x )
(1.74)
2.
r
r
r
r r
r
r
u ⊗ (αv + βw ) = αu ⊗ v + βu ⊗ w
(1.75)
3.
r r
r r r
r r r
r r r
(αv ⊗ u + βw ⊗ r ) ⋅ x = α ( v ⊗ u) ⋅ x + β ( w ⊗ r ) ⋅ x
r
r r
r
r r
= α[v ⊗ (u ⋅ x )] + β [w ⊗ (r ⋅ x )]
(1.76)
donde α y β son escalares. Por definición, el producto diádico no posee la propiedad
r r r r
conmutativa, es decir, u ⊗ v ≠ v ⊗ u .
La expresión (1.73) también la podemos expresar en el sistema cartesiano como:
r r
A = u ⊗ v = (u i eˆ i ) ⊗ ( v j eˆ j )
= u i v j (eˆ i ⊗ eˆ j )
= A ij (eˆ i ⊗ eˆ j )
A =
{
Tensor
A ij
{
componentes
eˆ i ⊗ eˆ j
1
424
3
base
(i, j = 1,2,3)
(1.77)
(i, j = 1,2,3)
(1.78)
Las componentes de un tensor de segundo orden serán representadas de diferentes formas
en el desarrollo de este libro:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
32
r r
A4
=2
u4
⊗3
v
1
↓
componentes
↓
(1.79)
r r
( A ) ij = (u ⊗ v ) ij = u i v j = A ij
Dichas componentes pueden estar explícitamente expresadas de forma matricial:
 A 11
( A ) ij = A ij = A =  A 21
 A 31
A 12
A 22
A 32
A 13 
A 23 
A 33 
(1.80)
Observemos que un tensor de segundo orden tiene 9 componentes independientes. A
continuación exponemos la representación de tensores de diferentes órdenes, dos, tres y
cuatro, en el sistema cartesiano:
U = U ij eˆ i ⊗ eˆ j
T = Tijk eˆ i ⊗ eˆ j ⊗ eˆ k
(i, j , k , l = 1,2,3)
(1.81)
I = I ijkl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l
OBS.: El orden de un tensor viene dado por el número de subíndices libres en sus
componentes.
OBS.: El número de componentes de un tensor viene dado por el máximo valor
del rango del subíndice, elevado al número de subíndices libres.
Ejemplo 1.12: ¿ Cuál es el orden de los tensores representados por sus componentes: v i ,
Φ ijk , Fijj , ε ij , C ijkl , σ ij ? Determinar cuantas componentes independientes tiene el tensor
C.
Solución: El orden del tensor viene dado por el número de subíndices libres, luego:
r r
Tensores de orden uno: v , F ; Tensores de segundo orden: ε , σ ; Tensor de tercer orden:
Φ ; Tensor de cuarto orden: C .
El número de componentes de un tensor viene dado por el máximo valor del rango del
subíndice, 3 si ( i = 1,2,3 ), elevado al número de subíndices libres. Es decir, para el tensor de
cuarto orden, el número de índices libres es 4, luego:
3 4 = (i = 3) × ( j = 3) × (k = 3) × (l = 3) = 81
El tensor de cuarto orden C ijkl tiene 81 componentes independientes.
Dados dos tensores de segundo orden A y B , a continuación definimos algunas
operaciones entre ellos:
ƒ
Suma
La suma de dos tensores del mismo orden resulta ser un tercer tensor de igual orden:
C = A +B =B + A
(1.82)
Las componentes del tensor resultante ( C ) viene representadas por:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
33
(C) ij = ( A + B) ij
C ij = A ij + B ij
(1.83)
que de forma matricial expresamos como:
ƒ
C =A+B
(1.84)
Multiplicación de un tensor por un escalar
La multiplicación de un tensor de segundo orden ( A ) por un escalar ( λ ) viene definido
por un tensor D , tal que:
D = λA en
componente

s →(D) ij = λ( A ) ij
(1.85)
en forma matricial:
 A 11
A = A 21
 A 31
A 13 
 λA 11

A 23  
→ λA = λA 21
λA 31
A 33 
A 12
A 22
A 32
λA 12
λA 22
λA 32
λA 13 
λA 23 
λA 33 
(1.86)
También se cumple que:
r
r
(λ A ) ⋅ v = λ ( A ⋅ v )
(1.87)
r
para cualquier vector v .
ƒ
Producto Escalar
r
El producto escalar de un tensor de segundo orden A por un vector x (tensor de orden
r
uno) resulta ser otro vector y (tensor de orden uno):
r
r
y = A⋅x
δ kl
= ( A jk eˆ j ⊗ eˆ k ) ⋅ ( x l eˆ l )
= A jk x l δ kl eˆ j
= A jk x k eˆ j
123
(1.88)
yj
= y j eˆ j
El producto escalar de dos tensores de segundo orden A y B es otro tensor de segundo
orden, verificándose que A ⋅ B ≠ B ⋅ A :
δ jk
δ jk
C = A ⋅ B = ( A ij eˆ i ⊗ eˆ j ) ⋅ (B kl eˆ k ⊗ eˆ l )
= A ij B kl δ jk eˆ i ⊗ eˆ l
= A ik B kl eˆ i ⊗ eˆ l
123
AB
D = B ⋅ A = (B ij eˆ i ⊗ eˆ j ) ⋅ ( A kl eˆ k ⊗ eˆ l )
= B ij A kl δ jk eˆ i ⊗ eˆ l
= B ik A kl eˆ i ⊗ eˆ l
123
= C il eˆ i ⊗ eˆ l
(1.89)
BA
= D il eˆ i ⊗ eˆ l
También se cumplen las siguientes propiedades:
A ⋅ (B + C) = A ⋅ B + A ⋅ C
A ⋅ (B ⋅ C) = ( A ⋅ B) ⋅ C
ƒ
(1.90)
Potencia de Tensores
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
34
El producto escalar (contracción simple) nos permite definir la potencia de tensores de
segundo orden, luego:
A 0 = 1 ; A1 = A ; A 2 = A ⋅ A
(1.91)
donde 1 es el tensor identidad de segundo orden, ver subapartado 1.5.2.5.
ƒ
Doble Producto Escalar
r
r
r
r
Consideremos dos diádicas, A = c ⊗ d y B = u ⊗ v , el doble producto escalar (doble
contracción) podrá ser definido de distintas formas A : B y A ⋅ ⋅B tal como se indica a
continuación.
Doble contracción (⋅ ⋅ ) :
(cr ⊗ dr ) ⋅ ⋅ (ur ⊗ vr ) = (cr ⋅ vr )(dr ⋅ ur )
(1.92)
δ il
δ jk
A ⋅ ⋅ B = ( A ij eˆ i ⊗ eˆ j )⋅ ⋅ (B kl eˆ k ⊗ eˆ l )
= A ij B kl δ jk δ il
(1.93)
= A ij B ji
=γ
(escalar )
Doble contracción ( : ):
(
)
( )
r r r r
r r r r
A : B = c ⊗ d : (u ⊗ v ) = (c ⋅ u) d ⋅ v
(1.94)
Según la definición del doble producto escalar, podemos demostrar que es conmutativo:
(
)
( )
( )
r r r r
r r r r
r r r r
B : A = (u ⊗ v ) : c ⊗ d = (u ⋅ c ) v ⋅ d = (c ⋅ u) d ⋅ v = A : B
(1.95)
En componentes:
δ ik
A : B = ( A ij eˆ i ⊗ eˆ j ) : (B kl eˆ k ⊗ eˆ l )
= A ij B kl δ ik δ jl
= A ij B ij
=λ
δ jl
(1.96)
(escalar )
Observemos que A : B ≠ A ⋅ ⋅B , excepto cuando al menos uno de los dos tensores sea
simétrico, i.e. A sym : B = A sym ⋅ ⋅ B , A : B sym = A ⋅ ⋅ B sym , A sym : B sym = A sym ⋅ ⋅ B sym
El doble producto escalar de un tensor de tercer orden ( S ) y uno de segundo ( B ), resulta:
(
)
( )cr
( )ar
r r r r r
r r r r
S : B = c ⊗ d ⊗ a : (u ⊗ v ) = (a ⋅ v ) d ⋅ u
r r r r r
r r r r
B : S = (u ⊗ v ) : c ⊗ d ⊗ a = (u ⋅ c ) v ⋅ d
(1.97)
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
(
)
1 TENSORES
35
Teniendo en cuenta la definición anterior, S : B en la base Cartesiana viene representada
por:
S ijk eˆ i ⊗ eˆ j ⊗ eˆ k : B pq eˆ p ⊗ eˆ q = S ijk B pq δ jp δ kq eˆ i = S ijk B jk eˆ i
(1.98)
La doble contracción de un tensor de cuarto orden C con uno de segundo orden ε queda
definido por:
C ijkl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l : ε pq eˆ p ⊗ eˆ q = C ijkl ε pq δ kp δ lq eˆ i ⊗ eˆ j
= C ijkl ε kl eˆ i ⊗ eˆ j
= σ ij eˆ i ⊗ eˆ j
(1.99)
donde σ ij son la componentes resultante de la operación σ = C : ε .
A continuación expresamos algunas propiedades del doble producto escalar ( : ):
a) A : B = B : A
b) A : (B + C ) = A : B + A : C
c) λ(A : B ) = (λA ) : B = A : (λB )
(1.100)
donde A , B, C son tensores de segundo orden y λ escalar.
A través del doble producto escalar, podemos obtener las componentes del tensor de
segundo orden A , según el sistema cartesiano, como:
( A ) ij = ( A kl eˆ k ⊗ eˆ l ) : (eˆ i ⊗ eˆ j ) = eˆ i ⋅ ( A kl eˆ k ⊗ eˆ l ) ⋅ eˆ j = A kl δ ki δ lj = A ij
(1.101)
r r
Consideremos dos vectores cualesquiera a , b y A un tensor de segundo orden,
demostramos que:
r
r
a ⋅ A ⋅ b = a p eˆ p ⋅ A ij eˆ i ⊗ eˆ j ⋅ b r eˆ r = a p A ij b r δ pi δ jr
= a i A ij b j = A ij (a i b j )
r r
= A : (a ⊗ b )
ƒ
(1.102)
Producto Vectorial
r
El producto vectorial de un tensor de segundo orden A por un vector x (tensor de orden
uno) resulta ser un tensor de segundo orden dado por:
r
A ∧ x = ( A ij eˆ i ⊗ eˆ j ) ∧ ( x k eˆ k )
=  ljk A ij x k eˆ i ⊗ eˆ l
(1.103)
donde empleamos la definición (1.67), es decir, eˆ j ∧ eˆ k =  ljk eˆ l . Hemos demostrado en el
r
(r r )
r r r
(r r ) r
Ejemplo 1.11 la siguiente relación a ∧ b ∧ c = (a ⋅ c ) b − a ⋅ b c , que también la podemos
representar a través de diádicas como:
[ar ∧ (br ∧ cr )]
j
= (a k c k )b j − (a k b k )c j = (b j c k − c j b k )a k
r r r r r
= b ⊗ c − c ⊗b ⋅a j
[(
r
) ]
(1.104)
r
En el caso particular cuando a = c podemos decir que:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
36
[ar ∧ (br ∧ ar )]
j
= (a k a k )b j − (a k b k )a j = (a k a k )b p δ jp − (a k b p δ kp )a j
[
]
[
]
= (a k a k )δ jp − (a k δ kp )a j b p = (a k a k )δ jp − a p a j b p
r r
r r r
= [(a ⋅ a)1 − a ⊗ a] ⋅ b j
{
}
(1.105)
Con lo cual podemos decir que las siguientes relaciones son válidas:
( ) (
)
r r
r
r r r r r r r r r r r
a ∧ (b ∧ c ) = (a ⋅ c ) b − a ⋅ b c = b ⊗ c − c ⊗ b ⋅ a
r r
r
r r
r r r
a ∧ (b ∧ a) = [(a ⋅ a)1 − a ⊗ a]⋅ b
1.5.1.1
(1.106)
Representación de las Componentes de un Tensor de Segundo
Orden en la Base Cartesiana
Como hemos visto, un vector que tiene 3 componentes independientes lo hemos
representado en el espacio cartesiano tal y como se indica en la Figura 1.12. Un tensor de
segundo orden arbitrario tiene 9 componentes independientes, luego necesitaríamos de un
hiperespacio para su presentación. A continuación presentamos un artilugio para hacer la
representación de las componentes del tensor de segundo orden en el espacio cartesiano.
Dado un tensor de segundo orden T , y su representación en la base cartesiana:
T = Tij eˆ i ⊗ eˆ j
= T11eˆ 1 ⊗ eˆ 1 + T12 eˆ 1 ⊗ eˆ 2 + T13 eˆ 1 ⊗ eˆ 3 +
+ T21eˆ 2 ⊗ eˆ 1 + T22 eˆ 2 ⊗ eˆ 2 + T23 eˆ 2 ⊗ eˆ 3 +
(1.107)
+ T31eˆ 3 ⊗ eˆ 1 + T32 eˆ 3 ⊗ eˆ 2 + T33 eˆ 3 ⊗ eˆ 3
Podemos obtener la proyección de T según la base ê k como:
T ⋅ eˆ k = Tij eˆ i ⊗ eˆ j ⋅ eˆ k = Tij eˆ i δ jk = Tik eˆ i = T1k eˆ 1 + T2 k eˆ 2 + T3k eˆ 3
(1.108)
Observemos que como resultado tenemos tres vectores ( k = 1,2,3 ):
r
k = 1 ⇒ Ti1eˆ i = T11eˆ 1 + T21eˆ 2 + T31eˆ 3 = t ( eˆ 1 )

r ( eˆ )
⇒
T ⋅ eˆ k = Tik eˆ i
(1.109)
k = 2 ⇒ Ti 2 eˆ i = T12 eˆ 1 + T22 eˆ 2 + T32 eˆ 3 = t 2
r (eˆ )

3
k = 3 ⇒ Ti 3 eˆ i = T13 eˆ 1 + T23 eˆ 2 + T33 eˆ 3 = t
r ˆ r ˆ
r ˆ
La representación de estos vectores t ( e1 ) , t (e 2 ) , t (e 3 ) , en la base cartesiana se muestra en la
Figura 1.14.
x3
r ˆ
t (e3 ) = T ⋅ eˆ 3
ê 3
r ˆ
t (e1 ) = T ⋅ eˆ 1
r ˆ
t (e 2 ) = T ⋅ eˆ 2
ê 2
x2
ê 1
x1
Figura 1.14: Vectores tensores en la base cartesiana.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
r
37
ˆ
Observemos también que t ( e1 ) es el tensor proyectado según la dirección ê1 cuyo versor
representamos por nˆ (i1) = [1,0,0] , es decir:
 T11
( T ⋅ nˆ ) i =  T21
 T31
T12
T22
T32
T31  1  T11 
ˆ
T23  0 =  T21  = t i( e1 )
T33  0  T31 
(1.110)
El mismo resultado (1.110) podía haber sido obtenido simplemente haciendo el producto
escalar de T dado por (1.107) por la base ê1 , es decir:
T ⋅ eˆ 1 = [ T11eˆ 1 ⊗ eˆ 1 + T12 eˆ 1 ⊗ eˆ 2 + T13 eˆ 1 ⊗ eˆ 3 +
+ T21eˆ 2 ⊗ eˆ 1 + T22 eˆ 2 ⊗ eˆ 2 + T23 eˆ 2 ⊗ eˆ 3 +
+ T31eˆ 3 ⊗ eˆ 1 + T32 eˆ 3 ⊗ eˆ 2 + T33 eˆ 3 ⊗ eˆ 3 ] ⋅ eˆ 1
r ˆ
= T11eˆ 1 + T21eˆ 2 + T31eˆ 3 = t ( e1 )
(1.111)
Luego, podemos representar las componentes de un tensor de segundo orden en la base
cartesiana tal y como se indica en la Figura 1.15.
Las componentes de la diagonal principal, T11 , T22 , T33 , están normales a los planos
definidos por los versores ê1 , ê 2 , ê 3 , respectivamente. Por ello denominamos de
componentes normales. Las componentes que están tangentes al plano denominamos de
componentes tangenciales, que corresponden a las componentes que están fuera de la diagonal
principal.
x3
 T11
Tij =  T21
 T31
T12
T22
T32
T13 
T23 
T33 
rˆ
t (e 3 )
T33 ê 3
rˆ
t (e 2 )
T13 ê1
T23 ê 2
T32 ê 3
T31ê 3
r ˆ
t ( e1 )
T22 ê 2
T21ê 2
T12 ê1
x2
T11ê1
x1
Figura 1.15: Representación de las componentes de un tensor de segundo en la base
cartesiana.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
38
NOTA: A lo largo del libro utilizaremos las siguientes notaciones:
Notación tensorial
Notación simbólica
A ⋅ B = ( A ij eˆ i ⊗ eˆ j ) ⋅ (B kl eˆ k ⊗ eˆ l )
(1.112)
= A ij B kl δ jk (eˆ i ⊗ eˆ l )
= A ij B jl (eˆ i ⊗ eˆ l )
base cartesiana
Notación indicial
Observemos que no se repite índices más que 2 veces ni en la notación simbólica ni en la
notación indicial. Observemos también que la notación indicial será equivalente a la
notación tensorial sólo cuando se trata de un escalar, e.g. A : B = A ijB ij = λ , a ⋅ b = a i b i .■
1.5.2
Propiedades de los Tensores
1.5.2.1
Transpuesta
Sea un tensor de segundo orden A representado por:
A = A ij (eˆ i ⊗ eˆ j )
(1.113)
La transpuesta del tensor A definimos como:
A T = A ji (eˆ i ⊗ eˆ j ) = A ij (eˆ j ⊗ eˆ i )
(1.114)
Si A ij son las componentes de A , las componentes de la transpuesta de A serán:
(A T ) ij = A ji
r
r
(1.115)
r
r
Si A = u ⊗ v , la transpuesta de A vendrá dada por A T = v ⊗ u :
r r T
= (u ⊗ v )
= u i eˆ i ⊗ v j eˆ j
= u i v j eˆ i ⊗ eˆ j
AT
(
(
= (A
ˆ ⊗ eˆ j
ij e i
)
T
)
)
T
T
r r
= v ⊗u
= v j eˆ j ⊗ u i eˆ i
= u i v j eˆ j ⊗ eˆ i
= v i eˆ i ⊗ u j eˆ j
= u j v i eˆ i ⊗ eˆ j
= A ij eˆ j ⊗ eˆ i
= A ji eˆ i ⊗ eˆ j
(1.116)
Sean A , B dos tensores y α , β escalares, las siguientes relaciones son válidas:
(A T )T = A
(αB + βA ) T = αB T + βA T
(B ⋅ A ) = A
T
AT
ˆ
T
(
: B = (A
⋅B
(1.117)
T
)
⊗ eˆ ) : (B
A : B T = A ij eˆ i ⊗ eˆ j : (B kl eˆ l ⊗ eˆ k ) = A ij B kl δ il δ jk = A ij B ji = A ⋅ ⋅ B
ij e j
i
ˆ ⊗ eˆ l ) = A ij B kl δ jk δ il = A ij B ji = A ⋅ ⋅ B
kl e k
(1.118)
La transpuesta de la matriz que contienen las componentes del tensor, se forma al cambiar
filas por columna y viceversa, es decir:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
 A 11
A = A 21
 A 31
A 12
A 22
A 32
A 13 
 A 11

transpuesta
T
A 23   → A =  A 21
 A 31
A 33 
39
T
A 12
A 22
A 13 
 A 11

A 23  =  A 12
 A 13
A 33 
A 32
A 21
A 22
A 23
A 31 
A 32 
A 33 
(1.119)
Ejemplo 1.13: Demostrar que las siguientes relaciones son válidas:
(
)
(
)
A : (B ⋅ C ) = B T ⋅ A : C = A ⋅ C T : B
donde A , B , C son tensores de segundo orden cualesquiera.
Solución: Demostraremos esta identidad a través de sus componentes:
(
A : (B ⋅ C ) = A ij eˆ i ⊗ e j : B lk eˆ l ⊗ e k ⋅ C pq eˆ p ⊗ eˆ q
= A ij B lk C pq eˆ i ⊗ e j : δ kp eˆ l ⊗ eˆ q
(
)
)
= A ij B lk C pq δ kp δ il δ jq = A ij B ik C kj
Observemos que cuando trabajamos en notación indicial la posición de las componentes
no importa, es decir:
A ij B ik C kj = B ik A ij C kj = A ij C kj B ik
Podemos ahora observar que la operación B ik A ij resultará un tensor de segundo orden
cuyas componentes son (B T ⋅ A ) kj luego, B ik A ij C kj = (B T ⋅ A ): C . Análogamente podemos
decir que A ij C kj B ik = (A ⋅ C T ): B .
r
r
Ejemplo 1.14: Demostrar que, si u , v son vectores y A un tensor de segundo orden, la
siguiente relación es válida:
r
r r
r
u⋅ AT ⋅ v = v ⋅ A ⋅u
Solución:
r
r
u⋅ AT ⋅ v
u i eˆ i ⋅ A jl eˆ l ⊗ eˆ j ⋅ v k eˆ k
r
r
= v ⋅ A ⋅u
= v k eˆ k ⋅ A jl eˆ j ⊗ eˆ l ⋅ u i eˆ i
u i A jl δ il v k δ jk
u l A jl v j
= v k δ kj A jl u i δ il
= v j A jl u l
1.5.2.2
Simetría y Antisimetría
1.5.2.2.1
Tensor Simétrico
Un tensor de segundo orden A es simétrico, i.e.: A ≡ A sym , si el tensor es igual a su
transpuesta:
A = A T en
componente

s → A ij = A ji
(1.120)
En forma de matriz:
T
→ A
A =A 
sym
 A 11
=  A 12
 A 13
A 12
A 22
A 23
A 13 
A 23 
A 33 
(1.121)
Podemos notar claramente que un tensor simétrico de segundo orden tiene 6 componentes
independientes: A 11 , A 22 , A 33 , A 12 , A 23 , A 13 .
Según ecuación (1.120) un tensor simétrico se puede representar por:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
40
A ij = A ji
A ij + A ij = A ij + A ji
(1.122)
2 A ij = A ij + A ji
A ij =
1
( A ij + A ji )
2
⇒
A=
1
(A + A T )
2
Un tensor de cuarto orden C , cuyas componentes son C ijkl , puede presentar:
Simetría menor:
C ijkl = C jikl = C ijlk = C jilk
(1.123)
C ijkl = C klij
(1.124)
Simetría mayor:
Luego, un tensor de cuarto orden es simétrico si presenta simetría menor y mayor. Un
tensor de cuarto orden no simétrico tiene 81 componentes independientes. Si presenta sólo
simetría menor, es decir, simetría en ij = ji (6) y simetría en kl = lk (6) , quedando el tensor
con 36 componentes independientes. Si además de simetría menor el tensor presenta
también simetría mayor, el tensor presenta 21 componentes independientes.
1.5.2.2.2
Tensor Antisimétrico
Un tensor A será antisimétrico, i.e.: A ≡ A anti , si:
A = − A T en
componente
 
s → A ij = − A ji
(1.125)
o aún:
T
→ A
A = −A 
anti
 0
= − A 12
 − A 13
A 12
0
− A 23
A 13 
A 23 
0 
(1.126)
Observemos que un tensor antisimétrico de segundo orden tiene 3 componentes
independientes: A 12 , A 23 , A 13 .
Según la condición (1.125) un tensor antisimétrico viene dado por:
A ij + A ij = A ij − A ji
2 A ij = A ij − A ji
1
A ij = ( A ij − A ji )
2
(1.127)
⇒
1
A = (A − A T )
2
Sea W un tensor antisimétrico, luego debe cumplir la relación (1.127):
Wij =
1
1
1
(Wij − W ji ) = (Wkl δ ik δ jl − Wkl δ jk δ il ) = Wkl (δ ik δ jl − δ jk δ il )
2
2
2
(1.128)
Utilizando la relación entre la delta de Kronecker y el operador de permutación dada por
(1.62) obtenemos que δ ik δ jl − δ jk δ il = − ijr  lkr y reemplazando en la expresión (1.128)
resulta:
1
Wij = − Wkl  ijr  lkr
2
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.129)
Por: Eduardo W.V. Chaves
1 TENSORES
41
Desarrollando el término Wkl  lkr para los índices mudos k , l sólo quedamos con los
siguientes términos distintos de cero:
Wkl  lkr = W12  21r + W13  31r + W2112 r + W23  32 r + W3113r + W32  23r
(1.130)
con lo que concluimos que:
r =1
⇒
r=2
⇒
r =3
⇒
Wkl  lkr = − W23 + W32 = −2W23 = 2 w1 

Wkl  lkr = W13 − W31 = 2W13 = 2w2  ⇒ Wkl  lkr = 2wr

Wkl  lkr = − W12 + W21 = −2W12 = 2w3 
(1.131)
donde hemos hecho los siguientes cambios de variables:
W13   0
W12
W13   0
− w3 w2 




W23  =  − W12
W23  =  w3
− w1 
0
0
(1.132)
W32
w1
0   − W13 − W23
0   − w2
0 
r
r
Definimos así el vector axil w correspondiente al tensor antisimétrico W . El módulo de w
 0
Wij =  W21
 W31
W12
0
viene dado por:
r
r r
ω 2 = w = w ⋅ w = w12 + w22 + w32 = W232 + W132 + W122
2
(1.133)
Reemplazando (1.131) en (1.129) y considerando que  ijr =  rij obtenemos que:
Wij = − wr  rij
(1.134)
Partiendo de la expresión (1.134) y multiplicando los dos miembros por  kij obtenemos
que:
 kij Wij = − wr  rij  kij = −2 wr δ rk = −2 wk
(1.135)
donde aplicamos la relación  rij  kij = 2δ rk obtenida en el Ejemplo 1.7, con lo que
concluimos que:
1
wk = −  kij Wij
2
(1.136)
La representación de las componentes del tensor antisimétrico y de su vector axil
correspondiente, en el sistema cartesiano, se puede apreciar en la Figura 1.16.
r
r
Sean a y b vectores arbitrarios y W un tensor antisimétrico, entonces se cumple que:
r
r
r
r
r
r r
r
b ⋅ W ⋅ a = a ⋅ W T ⋅ b = −a ⋅ W ⋅ b
(1.137)
luego si a = b resulta que:
r
r r
r
r r
− a ⋅ W ⋅ a = a ⋅ W ⋅ a = W : (a ⊗ a) = 0
(1.138)
r r
NOTA: Observar que (a ⊗ a) resulta un tensor de segundo orden simétrico. Más
adelante, demostraremos que el doble producto escalar entre un tensor simétrico y un
tensor antisimétrico resulta ser cero. ■
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
42
x3
r
w = w1eˆ 1 + w2 eˆ 2 + w3 eˆ 3
w3 = − W12
 0
Wij =  − W12
 − W13
W12
0
− W23
W13
W23
W13 
W23 
0 
W12
W12
x2
W23
w1 = − W23
W13
w2 = W13
x1
Figura 1.16: Componentes de un tensor antisimétrico.
r
Sean W un tensor antisimétrico y a un vector arbitrario, las componentes del producto
r
escalar W ⋅ a vienen dadas por:
Wij a j = Wi1a1 + Wi 2 a 2 + Wi 3 a 3
i = 1 ⇒ W11a1 + W12 a 2 + W13 a 3
i = 2 ⇒ W21a1 + W22 a 2 + W23 a 3
i =3⇒
(1.139)
W31a1 + W32 a 2 + W33 a 3
Considerando la propiedad del tensor antisimétrico, i.e., W11 = 0 , W22 = 0 , W33 = 0 , el
producto escalar (1.139) resulta:
i = 1 ⇒ W12 a 2 + W13 a 3
r
(W ⋅ a)i ⇒ i = 2 ⇒ W21a1 + W23 a 3
i = 3 ⇒ W a + W a
31 1
32 2

(1.140)
Fijemos que las componentes anteriores son las mismas que resultan de la operación:
eˆ 1
r r
w ∧ a = w1
a1
eˆ 2
eˆ 3
w2
a2
w3
a3
= (− w3 a 2 + w2 a 3 ) eˆ 1 + (w3 a1 − w1a 3 ) eˆ 2 + (− w2 a1 + w1a 2 ) eˆ 3
= (W12 a 2 + W13 a 3 )eˆ 1 + (W21a1 + W23 a 3 ) eˆ 2 + (W31a1 + W32 a 2 ) eˆ 3
(1.141)
donde se cumple que w1 = −W23 = W32 , w2 = W13 = −W31 , w3 = −W12 = W21 . Luego, dado un
r
tensor antisimétrico W , y el vector axil w correspondiente a W se cumple que:
r r r
W⋅a = w ∧ a
(1.142)
r
para todo vector a . La relación anterior podría haber sido obtenida a través de la
definición de las componentes de W dada por (1.134), i.e.:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
43
r
r r
(W ⋅ a) i = Wik a k = − w j  jik a k =  ijk w j a k = ( w ∧ a) i
r
(1.143)
r
Podemos representar el vector axil w por su módulo, w = ω , y por un versor según la
r
r
dirección de w como w = ωê1* , luego la expresión (1.142) puede aun ser expresada por:
r r r
r
W ⋅ a = w ∧ a = ωeˆ 1* ∧ a
(1.144)
Además si escogemos dos versores ê *2 , ê *3 que constituyan una base ortonormal con ê1* ,
ver Figura 1.17, tal que:
eˆ 1* = eˆ *2 ∧ eˆ *3
Podemos
entonces
eˆ *2 = eˆ *3 ∧ eˆ 1*
;
representar
el
eˆ *3 = eˆ 1* ∧ eˆ *2
;
r
a
vector
r
a = a1* eˆ 1* + a *2 eˆ *2 + a *3 eˆ *3 , luego:
r
r
W ⋅ a = ωeˆ 1* ∧ a = ωeˆ 1* ∧ (a1* eˆ 1* + a *2 eˆ *2 + a *3 eˆ *3 )
en
esta
(1.145)
nueva
= ω (a1* eˆ 1* ∧ eˆ 1* + a *2 eˆ 1* ∧ eˆ *2 + a *3 eˆ 1* ∧ eˆ *3 ) = ω (a *2 eˆ *3 − a *3 eˆ *2 )
1
424
3
1
424
3
1
424
3
[
=0ˆ
=eˆ *3
]
r
= ω (eˆ *3 ⊗ eˆ *2 − eˆ *2 ⊗ eˆ *3 ) ⋅ a
=− eˆ *2
base
como
(1.146)
Con lo cual podemos representar un tensor antisimétrico como:
W = ω (eˆ *3 ⊗ eˆ *2 − eˆ *2 ⊗ eˆ *3 )
(1.147)
r
w = ωê1*
ê*2
ê3
ê 2
ê1*
ê1
ê*3
Figura 1.17: bases ortonormales.
Aprovechando la representación del tensor antisimétrico (1.147), podemos obtener la
proyección del tensor W según las direcciones ê1* , ê *2 , ê *3 :
r
W ⋅ eˆ 1* = 0
;
W ⋅ eˆ *2 = ωeˆ *3
;
W ⋅ eˆ *3 = −ωeˆ *2
(1.148)
También podemos verificar que se cumple lo siguiente:
[
⋅ [ω (eˆ
] ⋅ eˆ
⊗ eˆ )] ⋅ eˆ
eˆ *3 ⋅ W ⋅ eˆ *2 = eˆ *3 ⋅ ω (eˆ *3 ⊗ eˆ *2 − eˆ *2 ⊗ eˆ *3 )
*
2
=ω
eˆ *2 ⋅ W ⋅ eˆ *3 = eˆ *2
*
3
= −ω
*
3
⊗ eˆ *2 − eˆ *2
*
3
(1.149)
Luego, en este nuevo espacio podemos representar las componentes del tensor W como:
Wij*
0 
0 0

= 0 0 − ω 
0 ω 0 
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.150)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
44
En la Figura 1.18 podemos apreciar dichas componentes y la representación del vector axil.
Observemos también que, si tomamos otros dos versores cualesquiera (normales entre sí)
definidos en el plano eˆ *2 − eˆ *3 nos proporcionarán las mismas componentes que (1.150).
Es interesante observar que las componentes de W en las bases ( eˆ i ⊗ eˆ j ) y ( eˆ *i ⊗ eˆ *j ) son
distintas, ver Figura 1.18 y Figura 1.16. Más adelante obtendremos la ley que gobierna dicha
transformación, i.e. conocidas las componentes en un sistema, a través de ley de
transformación podemos obtener las componentes en otra base.
x3
r
w = ωê1*
x2
ê*2
Wij*
0 
0 0

= 0 0 − ω 
0 ω 0 
ê1*
ω
x1
ω
r
ω = w = W232 + W132 + W122
ê*3
Figura 1.18: Componentes del tensor antisimétrico en el espacio definido por el vector axil.
1.5.2.2.3
Descomposición Aditiva de Tensores en una Parte Simétrica y Antisimétrica
Cualquier tensor puede ser descompuesto (de forma adicional) en una parte simétrica A sym
y en otra antisimétrica A anti :
A=
1
1
( A + A T ) + ( A − A T ) = A sym + A anti
2 4243 1
2 4243
1
A
sym
A
(1.151)
anti
en componentes:
A ijsym =
1
( A ij + A ji )
2
y A ijanti =
1
( A ij − A ji )
2
(1.152)
Observemos que, si A y B son tensores de segundo orden cualesquiera, se cumple que:
(A
T
⋅B ⋅ A)
sym
(
) (
)
[
T
1 T
1
A ⋅ B ⋅ A + A T ⋅ B ⋅ A  = A T ⋅ B ⋅ A + A T ⋅ BT ⋅ A




2
2
1
= A T ⋅ B + BT ⋅ A
2
T
= A ⋅ B sym ⋅ A
=
[
]
]
(1.153)
Ejemplo 1.15: Si σ es un tensor de segundo orden simétrico y W es un tensor de
segundo orden antisimétrico. Demostrar que σ : W = 0 .
Solución:
σ : W = σ ij (eˆ i ⊗ eˆ j ) : Wlk (eˆ l ⊗ eˆ k ) = σ ij Wlk δ il δ jk = σ ij Wij (escalar)
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
Desarrollando
45
σ ij Wij = σ1 j W1 j + σ 2 j W2 j + σ 3 j W3 j
123
1
424
3
1
424
3
σ31W31
σ21W21
σ11W11
+
+
+
σ32 W32
σ 22 W22
σ12 W12
+
+
+
σ33W33
σ23W23
σ13W13
Considerando la propiedad de un tensor simétrico σ12 = σ 21 , σ 31 = σ13 , σ 32 = σ 23 y
antisimétrico W11 = W22 = W33 = 0 , W21 = − W12 , W31 = − W13 , W32 = − W23 , resultando:
c.q.d.
σ :W =0
Ejemplo 1.16: Demostrar que:
r
r
r
r
a) M ⋅ Q ⋅ M = M ⋅ Q sym ⋅ M
b) A : B = A sym : B sym + A anti : B anti
r
donde , M es un vector y Q , A , y B son tensores de segundo orden.
Solución:
a)
(
)
r
r r
r
M ⋅ Q ⋅ M = M ⋅ Q sym + Q anti ⋅ M
r
r r
r
= M ⋅ Q sym ⋅ M + M ⋅ Q anti ⋅ M
r
r
r
r
Ya que el producto: M ⋅ Q anti ⋅ M = Q anti : M ⊗ M = 0 , resulta que:
r
r r
r
M ⋅ Q ⋅ M = M ⋅ Q sym ⋅ M c.q.d.
(
)
b)
A :B
= ( A sym + A anti ) : (B sym + B anti )
anti
sym
anti
= A sym : B sym + 1
A sym
:B
A anti
:B
: B anti
42
43 + 1
42
43 + A
=0
= A sym : B sym + A anti : B anti
Luego como consecuencia tenemos que:
A : B sym = A sym : B sym
r
;
=0
A : B anti = A anti : B anti c.q.d.
r
Ejemplo 1.17: ¿La relación n ⋅ T = T ⋅ n es válida siempre? Siendo T un tensor de segundo
r
orden y n un vector. En el supuesto de que la relación no sea válida, ¿para qué caso
particular lo sería?
Solución:
r
n ⋅ T = n i eˆ i ⋅ Tkl (eˆ k ⊗ eˆ l )
= n i Tkl δ ik eˆ l
y
r
T ⋅ n = Tlk (eˆ l ⊗ eˆ k ) ⋅ n i eˆ i
= n i Tlk δ ki eˆ l
= n k Tkl eˆ l
= n k Tlk eˆ l
r
r
r
r
Con lo que comprobamos que n k Tkl ≠ n k Tlk , luego n ⋅ T ≠ T ⋅ n . La relación n ⋅ T = T ⋅ n
sólo será válida cuando el tensor T sea simétrico.
r
r
r
Ejemplo 1.18: Obtener el vector axil w asociado al tensor antisimétrico ( x ⊗ a ) anti .
r
r
r
Expresar w en función de x y a .
Solución:
r
Sea z un vector arbitrario, se cumple que:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
46
r r
r r r
( x ⊗ a ) anti ⋅ z = w ∧ z
r r
r
donde w es el vector axil asociado a ( x ⊗ a ) anti . Teniendo en cuenta que:
r r
r r
1 r r r r
1 r r
( x ⊗ a ) anti = ( x ⊗ a ) − ( x ⊗ a ) T = [ x ⊗ a − a ⊗ x ]
2
2
[
]
podemos aún decir que:
1 r r r r r r r
[x ⊗ a − a ⊗ x ] ⋅ z = w ∧ z
2
r r r r r
r r
⇒ [ x ⊗ a − a ⊗ x ] ⋅ z = 2w ∧ z
r r r r r r
r r
Utilizando la identidad (1.104) se cumple que [x ⊗ a − a ⊗ x ] ⋅ z = z ∧ ( x ∧ a ) , luego:
[xr ⊗ ar − ar ⊗ xr ] ⋅ zr = zr ∧ ( xr ∧ ar ) = (ar ∧ xr ) ∧ zr = 2wr ∧ zr
con lo cual, concluimos que:
r 1 r r
r r
w = (a ∧ x ) es el vector axil asociado al tensor ( x ⊗ a ) anti
2
1.5.2.3
Cofactor de un Tensor. Adjunta de un Tensor
r
Dado un tensor A , representamos el cofactor de A como cof(A ) . Dados dos vectores a
r
y b existe un único tensor cof( A ) asociado al tensor A tal que:
r
r
r r
cof( A ) ⋅ (a ∧ b) = ( A ⋅ a) ∧ ( A ⋅ b)
(1.154)
Definimos la adjunta de un tensor A como:
adj( A ) = [cof (A )]
T
(1.155)
donde se cumple que:
[adj(A)]T
= adj( A T )
(1.156)
Las componentes de cof(A ) podemos obtener de la siguiente manera:
[cof( A)]it  tpr a p b r =  ijk A jp a p A kr b r
⇒ [cof( A )]it  tpr =  ijk A jp A kr
(1.157)
Multiplicando ambos lados de la igualdad por  qpr y además considerando que
 tpr  qpr = 2δ tq , concluimos que:
[cof(A)]it  tpr =  ijk A jp A kr
⇒
[cof( A)]it 1
tpr  qpr =  ijk  qpr A jp A kr
4
24
3
= 2δ tq
⇒ [cof( A )]iq
1.5.2.4
1
=  ijk  qpr A jp A kr
2
(1.158)
Traza de un Tensor
Antes de definir la traza de un tensor de segundo orden definimos la traza de su base:
Tr (eˆ i ⊗ eˆ j ) = eˆ i ⋅ eˆ j = δ ij
(1.159)
Luego la traza de un tensor A es la suma de las componentes de su diagonal principal:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
47
Tr ( A ) = Tr ( A ij eˆ i ⊗ eˆ j ) = A ij Tr (eˆ i ⊗ eˆ j ) = A ij (eˆ i ⋅ eˆ j ) = A ij δ ij = A ii
= A 11 + A 22 + A 33
(1.160)
Análogamente podemos decir que:
r r
r r
Tr (u ⊗ v ) = Tr (u ⊗ v ) = u i v j Tr (eˆ i ⊗ eˆ j ) = u i v j (eˆ i ⋅ eˆ j ) = u i v j δ ij = u i v i
r r
= u1 v 1 + u 2 v 2 + u 3 v 3 = u ⋅ v
(1.161)
NOTA: Podemos adelantar que la traza de un tensor es un invariante, es decir, es
independiente del sistema de referencia. ■
Dados dos tensores A y B :
ƒ
La traza de la transpuesta de un tensor es igual a la traza del tensor:
( )
Tr A T = Tr (A )
ƒ
(1.162)
La traza de la suma de estos dos tensores será la suma de la traza de los tensores:
Tr(A + B ) = Tr (A ) + Tr (B )
(1.163)
La demostración es muy sencilla bastando expresar en términos de componentes la
expresión anterior:
Tr(A + B ) = Tr (A ) + Tr (B )
[(A 11 + B 11 ) + (A 22 + B 22 ) + (A 33 + B 33 )] = (A 11 + A 22 + A 33 ) + (B 11 + B 22 + B 33 )
ƒ
La traza del producto escalar será:
[
Tr(A ⋅ B ) = Tr ( A ij eˆ i ⊗ eˆ j ) ⋅ (B lm eˆ l ⊗ eˆ m )
= A ij B lm δ jl Tr (eˆ i ⊗ eˆ m )
144244
3
[
]
(1.164)
]
(1.165)
δ im
= A il B li = A ⋅ ⋅B = Tr ( B ⋅ A )
Análogamente podemos obtener:
Tr(A ⋅ B ⋅ C ) = Tr (B ⋅ C ⋅ A ) = Tr (C ⋅ A ⋅ B ) = A ij B jk C ki
(1.166)
Luego, es fácil demostrar que las siguientes relaciones son válidas:
( )
Tr (A ) = A ii , [Tr ( A )] = Tr ( A ) Tr ( A ) = A ii A jj , Tr(A ⋅ A ) = Tr A 2 = A il A li
2
( )
Tr(A ⋅ A ⋅ A ) = Tr A 3 = A ij A jk A ki
(1.167)
Podemos escribir el doble producto escalar ( : ) en función de la traza como:
A : B = A ij B ij
= A kj B lj δ ik δ il
= A kj B lj δ kl
123
( A⋅BT )
(
kl
= A ⋅ BT
)
kk
= Tr ( A ⋅ B )
T
= A ik B il δ jk δ jl
= A ik B il δ kl
123
( AT ⋅B )
(
kl
= AT ⋅B
= Tr ( A
T
(1.168)
)
kk
⋅ B)
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
48
Ejemplo 1.19: Demostrar las siguientes identidades:
(T ) = (T )
m T
Solución:
(T )
m T
T m
;
( )
= Tr T m .
( )
c.q.d.
Tr T T
= (T ⋅ T L T ) = T T ⋅ T T L T T = T T
T
m
m
( )
Para la segunda demostración utilizaremos la propiedad de la traza Tr (T T ) = Tr (T )
m
T
c.q.d.
Tr (T T ) = Tr (T m ) = Tr (T m )
1.5.2.5
Tensores Particulares
1.5.2.5.1
Tensores Identidad
ƒ
Tensor identidad de segundo orden:
1 = δ ij eˆ i ⊗ eˆ j = eˆ i ⊗ eˆ i = 1 eˆ i ⊗ eˆ j
(1.169)
donde 1 es la matriz con las componentes del tensor 1 . δ ij es conocido como el símbolo
delta de Kronecker, definido en (1.47):
 1 si i = j

δ ij = 
 0 si i ≠ j

ƒ
(1.170)
Tensores identidades de cuarto orden:
I = 1⊗1 = δ ik δ jl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l = I ijkl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l
(1.171)
I = 1⊗1 = δ il δ jk eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l = I ijkl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l
(1.172)
I = 1 ⊗ 1 = δ ij δ kl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l = I ijkl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l
(1.173)
Con lo cual, dado un tensor de segundo orden arbitrario, A , se cumplen que:
(
)(
I : A = δ ik δ jl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l : A pq eˆ p ⊗ eˆ q
= δ ik δ jl A pq δ kp δ lq eˆ i ⊗ eˆ j
(
(
= δ ik δ jl A kl eˆ i ⊗ eˆ j
= A ij eˆ i ⊗ eˆ j
(
)
)
)
)
(1.174)
=A
y
(
)(
I : A = δ il δ jk eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l : A pq eˆ p ⊗ eˆ q
= δ il δ jk A pq δ kp δ lq eˆ i ⊗ eˆ j
(
(
= δ il δ jk A kl eˆ i ⊗ eˆ j
= A ji eˆ i ⊗ eˆ j
(
=A
)
)
)
)
(1.175)
T
y
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
(
49
)(
I : A = δ ij δ kl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l : A pq eˆ p ⊗ eˆ q
= δ ij δ kl A pq δ kp δ lq eˆ i ⊗ eˆ j
= δ ij δ kl A kl eˆ i ⊗ eˆ j
(
(
(
= A kk δ ij eˆ i ⊗ eˆ j
= Tr ( A )1
)
)
)
)
(1.176)
La parte simétrica del tensor de identidad de cuarto orden viene definido como:
I sym ≡ I =
(
)
(
1
1
componente

s → I ijkl = δ ik δ jl + δ il δ jk
1⊗1 + 1⊗1 en
2
2
)
(1.177)
La propiedad que presenta el producto tensorial ⊗ se presenta a continuación.
Consideremos el tensor identidad de segundo orden un tensor de segundo orden
1 = δ ij eˆ i ⊗ eˆ j , luego definimos el producto tensorial ⊗ como:
(
)
(
1⊗1 = δ ij eˆ i ⊗ eˆ j ⊗(δ kl eˆ k ⊗ eˆ l ) = δ ij δ kl eˆ i ⊗ eˆ k ⊗ eˆ j ⊗ eˆ l
)
(1.178)
que es lo mismo que:
(
1⊗1 = I = δ ik δ jl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l
)
(1.179)
Y el producto tensorial ⊗ como:
(
)
(
1⊗1 = δ ij eˆ i ⊗ eˆ j ⊗(δ kl eˆ k ⊗ eˆ l ) = δ ij δ kl eˆ i ⊗ eˆ l ⊗ eˆ k ⊗ eˆ j
ó
(
1⊗1 = I = δ il δ jk eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l
)
(1.180)
)
(1.181)
La parte antisimétrica de I será:
I anti =
(
)
(
1
1
anti
componente

s → I ijk
δ ik δ jl − δ il δ jk
1⊗1 − 1⊗1 en
l =
2
2
)
(1.182)
r
Se puede demostrar que, dado un tensor de segundo orden A y un vector b las siguientes
relaciones son válidas:
r
r
b ⋅1 = b
I:A = A
I sym : A = A sym
;
A : 1 = Tr (A ) = A ii
( )
: 1 = Tr (A ) = Tr (A ⋅ A ⋅ A ) = A
(1.183)
A 2 : 1 = Tr A 2 = Tr (A ⋅ A ) = A il A li
A3
1.5.2.5.2
3
ij A jk A ki
Pseudo-Tensor Levi-Civita
El Pseudo-Tensor Levi-Civita, también conocido como Tensor de Permutación, es un pseudotensor de tercer orden definido como:
 =  ijk eˆ i ⊗ eˆ j ⊗ eˆ k
(1.184)
donde  ijk son las componentes del operador de permutación definido en (1.55).
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
50
Ejemplo 1.20: Demostrar que: T : 1 = Tr (T ) .
Solución:
T : 1 = Tij eˆ i ⊗ eˆ j : δ kl eˆ k ⊗ eˆ l
= Tij δ kl δ ik δ jl
= Tij δ ij = Tii = T jj
= Tr ( T )
c.q.d.
Ejemplo 1.21: Probar que si σ y D son tensores de segundo orden la siguiente relación es
válida:
σ ⋅ ⋅ D = Tr (σ ⋅ D )
Solución: Basándonos en lo que fue demostrado en (1.93), podemos decir que:
σ ⋅ ⋅ D = σ ij D ji
= σ kj D jl δ ik δ il = σ kj D jl δ lk
= σ kj D jl δ lk
123
( σ⋅D )
kl
= (σ ⋅ D) kl δ lk = (σ ⋅ D) kk = (σ ⋅ D) ll
= Tr (σ ⋅ D) c.q.d.
Una segunda alternativa para la demostración sería:
σ ⋅ ⋅ D = σ ij D ji = σ ij D jk δ ik
= (σ ⋅ D ) : 1
= Tr (σ ⋅ D )
1.5.2.6
c.q.d.
Determinante de un Tensor
El determinante de un tensor es un escalar y también es un invariante:
det ( A ) ≡ A
=  ijk A 1i A 2 j A 3k =  ijk A i1 A j 2 A k 3
144244
3
(1.185)
AT
El determinante de un tensor es igual al determinante de la matriz que contiene las
componentes del tensor.
La demostración de (1.185) puede hacerse partiendo directamente del determinante:
A 11
A 12
A 13
det ( A ) = A = A 21 A 22 A 23
A 31 A 32 A 33
= A 11 ( A 22 A 33 − A 23 A 32 ) − A 21 ( A 12 A 33 − A 13 A 32 ) + A 31 ( A 12 A 23 − A 13 A 22 )
= A 11 (1 jk A j 2 A k 3 ) − A 21 (− 2 jk A j 2 A k 3 ) + A 31 ( 3 jk A j 2 A k 3 )
= 1 jk A 11 A j 2 A k 3 +  2 jk A 21 A j 2 A k 3 +  3 jk A 31 A j 2 A k 3
=  ijk A i1 A j 2 A k 3
(1.186)
Algunas consideraciones sobre el determinante de tensores:
det (1) = 1
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.187)
Por: Eduardo W.V. Chaves
1 TENSORES
ƒ
51
Podemos concluir de (1.185) que:
det ( A T ) = det ( A )
ƒ
(1.188)
También podemos demostrar que las siguientes relaciones son válidas:
det ( A ⋅ B) = det ( A )det (B)
det (αA ) = α 3 det ( A )
(1.189)
siendo α un escalar
ƒ
Un tensor (A ) se dice que es singular si det ( A ) = 0 .
ƒ
Intercambiando dos líneas o columnas el signo del determinante cambia.
ƒ
Si todos elementos de una fila o columna son cero, el determinante es cero.
ƒ
Multiplicando todos los elementos de una fila o columna por una constante c
(escalar), el determinante queda: c A .
Ejemplo 1.22: Demostrar que: A  tpq =  rjk A rt A jp A kq
Solución: Sabemos que:
A =  rjk A r1 A j 2 A k 3
(1.190)
A  tpq =  rjk  tpq A r1 A j 2 A k 3
Como lo visto anteriormente, ecuación (1.61), la expresión  rjk  tpq podrá ser expresada en
función de la delta de Kronecker como:
δ rt δ rp δ rq
 rjk  tpq = δ jt δ jp δ jq
(1.191)
δ kt δ kp δ kq
= δ rt δ jp δ kq + δ rp δ jq δ kt + δ rq δ jt δ kp − δ rq δ jp δ kt − δ jq δ kp δ rt − δ kq δ jt δ rp
Reemplazando la expresión anterior (1.191) en la expresión (1.190), y utilizando la
propiedad del operador de sustitución obtenemos que:
A  tpq = A t1 A p 2 A q 3 + A p1 A q 2 A t 3 + A q1 A t 2 A p 3 − A q1 A p 2 A t 3 − A t1 A q 2 A p 3 − A p1 A t 2 A q 3
= A t1 ( 1 jk A pj A qk ) + A t 2 ( 2 jk A pj A qk ) + A t 3 ( 3 jk A pj A qk )
=  rjk A rt A jp A kq =  rjk A tr A pj A qk
c.q.d.
1
6
Ejemplo 1.23: Demostrar que: A =  rjk  tpq A rt A jp A kq
Solución:
Partiendo del problema anterior: A  tpq =  rjk A rt A jp A kq y multiplicando ambos lados por
 tpq , resulta:
A  tpq  tpq =  rjk  tpq A rt A jp A kq
(1.192)
Utilizando la propiedad definida anteriormente en la ecuación (1.62), obtenemos que
 tpq  tpq = δ tt δ pp − δ tp δ tp = δ tt δ pp − δ tt = 6 . Luego, la relación (1.192) resulta:
A =
Ejemplo 1.24: Demostrar que:
(
1
 rjk  tpq A rt A jp A kq
6
)
r r
r r
det µ1 + αa ⊗ b = µ 3 + µ 2 α a ⋅ b
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
c.q.d.
(1.193)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
52
Solución: Si denotamos por A ij µδ ij + αa i b j , el determinante de A viene dado por
A =  ijk A i1 A j 2 A k 3 , donde A i1 = µδ i1 + αa i b1 , A j 2 = µδ j 2 + αa j b 2 y A k 3 = µδ k 3 + αa k b 3 ,
luego podemos decir que:
r r
det µ1 + αa ⊗ b =  ijk (µδ i1 + αa i b1 )(µδ j 2 + αa j b 2 )(µδ k 3 + αa k b 3 )
(1.194)
Desarrollando la expresión (1.194) obtenemos que:
r r
det µ1 + αa ⊗ b =  ijk [µ 3 δ i1δ j 2 δ k 3 + µ 2 αa k b 3 δ i1δ j 2 + µ 2 αa j b 2 δ i1δ k 3 + µ 2 αa i b 1δ j 2 δ k 3 +
(
)
(
)
+ µα a j b 2 a k b 3 δ i1 + µα 2 a i a k b 1b 3 δ j 2 + µα 2 a i a j b 1b 2 δ k 3 + α 3 a i a j a k b 1b 2 b 3
2
]
Observemos que:
µ 3  ijk δ i1δ j 2 δ k 3 = µ 3 123 = µ 3
µ 2 α ( ijk a k b 3 δ i1δ j 2 +  ijk a j b 2 δ i1δ k 3 +  ijk a i b1δ j 2 δ k 3 ) =
r r
µ 2 α (12 k a k b 3 +  1 j 3 a j b 2 +  i 23 a i b1 ) = µ 2 α (a 3b 3 + a 2 b 2 + a1b1 ) = µ 2 α (a ⋅ b)
 ijk a i a k b1b 3 δ j 2 =  i 2 k a i a k b1b 3 = a1a 3b1b 3 − a 3 a1b1b 3 = 0
 ijk a i a j b1b 2 δ k 3 =  ij 3 a i a j b1b 2 =  123 a1 a 2 b1b 2 −  213 a 2 a1b1b 2 = 0
 ijk a i a j a k b1b 2 b 3 = 0
Fijemos que no hacía falta expandir los términos  ijk a i a k b1b 3 δ j 2 ,  ijk a i a j b1b 2 δ k 3 ,
 ijk a i a j a k b1b 2 b 3 ,
para
saber
que
son
iguales
a
cero,
ya
que
r r
= (a ∧ a) j b 1b 3 δ j 2 = 0 y análogamente para los otros términos. Con lo que
 ijk a i a k b1b 3 δ j 2
hemos demostrado que:
(
)
r r
r r
det µ1 + αa ⊗ b = µ 3 + µ 2 α a ⋅ b
Para µ = 1 tenemos que:
(
c.q.d.
)
r r
r r
det 1 + αa ⊗ b = 1 + α a ⋅ b
Análogamente, se puede demostrar que:
r r
det αa ⊗ b = α 3  ijk a i a j a k b1b 2 b 3 = 0
(
)
También podemos demostrar que se cumple la siguiente relación:
[
]
[
]
r r
r r
r r
r r r r
r r
r r
(1.195)
det 1 + α (a ⊗ b) + β (b ⊗ a) = 1 + α (a ⋅ b) + β (a ⋅ b) + αβ (a ⋅ b) 2 − (a ⋅ a)(b ⋅ b)
r r
r r
donde α , β son escalares. Si β = 0 recaemos en la expresión det 1 + αa ⊗ b = 1 + αa ⋅ b .
Si α = β , obtenemos que:
r r
r r
r r
r r
r r 2 r r r r
det 1 + α a ⊗ b + α b ⊗ a = 1 + α a ⋅ b + α a ⋅ b + α 2  a ⋅ b − (a ⋅ a) b ⋅ b 


(1.196)
r
r
2
r
r
= 1 + α 2 a ⋅ b − α a ∧ b 


(
)
(
( ) ( ) ( )
( ) ( )
(r r )
)
( )
( ) (r r )
r r r r
donde hemos utilizado la propiedad a ⋅ b − (a ⋅ a) b ⋅ b = − a ∧ b , ver Ejemplo 1.1.
2
2
También podemos demostrar que la siguiente relación es válida:
(1.197)
det (α A + β B ) = α 3 det (A ) + α 2 β Tr[B ⋅ adj( A )] + αβ 2 Tr[A ⋅ adj(B)] + β 3 det (B )
r r
Para el caso particular cuando α = 1 , A = 1 , B = a ⊗ b , y además teniendo en cuenta que
r r
r r
det a ⊗ b = 0 , y cof a ⊗ b = 0 , concluimos que:
(
)
(
)
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
(
[
)
53
]
[
]
(1.198)
]
(1.199)
r r
r r
r r
r r
det 1 + βa ⊗ b = det (1) + βTr a ⊗ b ⋅ 1 = 1 + βTr a ⊗ b = 1 + βa ⋅ b
cuya relación ya fue demostrada anteriormente.
Podemos demostrar que la siguiente propiedad es válida:
[
]
[
r
r
r
r r r
( A ⋅ a) ⋅ ( A ⋅ b) ∧ ( A ⋅ c ) = det ( A ) a ⋅ (b ∧ c)
Para la demostración partiremos de la definición del triple producto escalar dada por (1.69),
r r r
a ⋅ b ∧ c =  ijk a i b j c k , y multiplicamos por ambos lados de la igualdad por el determinante
del tensor A , resultando:
(
)
(
)
r r r
a ⋅ b ∧ c A =  ijk a i b j c k A
(1.200)
Fue demostrado en el Ejemplo 1.22 que se cumple que A  ijk =  pqr A pi A qj A rk , con lo
cual:
(
)
r r r
a ⋅ b ∧ c A =  ijk a i b j c k A
=  pqr A pi A qj A rk a i b j c k
(1.201)
=  pqr ( A pi a i )( A qj b j )( A rk c k )
r
r
r
= ( A ⋅ a) ⋅ ( A ⋅ b) ∧ ( A ⋅ c )
[
1.5.2.7
]
Inversa de un Tensor
La inversa de un tensor A es un tensor A −1 , definido como:
si A ≠ 0 ⇔ ∃ A −1 A ⋅ A −1 = A −1 ⋅ A = 1
(1.202)
En notación indicial:
si A ≠ 0 ⇔ ∃ A ij−1 A ik A kj−1 = A ik−1 A kj = δ ij
(1.203)
La expresión de la inversa podemos obtener partiendo de la definición de la adjunta de un
r
r r
r
tensor dada por (1.154), adj( A T ) ⋅ (a ∧ b) = ( A ⋅ a) ∧ ( A ⋅ b) , y multiplicamos escalarmente
r
por el vector d , resultando:
{[adj(A)]
T
⋅ (a ∧ b)}⋅ d = [( A ⋅ a) ∧ ( A ⋅ b)]⋅ d
r
r
r
r
r
r
[
]
r
r
r
= [( A ⋅ a) ∧ ( A ⋅ b)]⋅ A ⋅ A
⋅
d
12r3
r
r
r
= ( A ⋅ a) ∧ ( A ⋅ b) ⋅ 1 ⋅ d
(1.204)
−1
=c
Utilizando la definición (1.201), podemos decir que también se cumple que:
(
)
[
]
r
r
r
r r r
c ⋅ a ∧ b A = ( A ⋅ c ) ⋅ ( A ⋅ a) ∧ ( A ⋅ b)
r
r r r
r
r
a ∧ b ⋅ c A = ( A ⋅ a) ∧ ( A ⋅ b) ⋅ ( A ⋅ c)
(1.205)
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
(
)
[
]
Luego:
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
54
{[adj(A)]
T
⋅ (a ∧ b)}⋅ d = [( A ⋅ a) ∧ ( A ⋅ b)]⋅ A ⋅ A −1 ⋅ d
r
r r
= A (a ∧ b )⋅ A −1 ⋅ d
r
r
r
r
r
r
r
r
(1.206)
r
r
r
El vector resultante de la operación (a ∧ b) representamos por el vector p = (a ∧ b) , con
lo cual la expresión anterior en notación indicial queda:
{[adj(A)]ki p k }di = A p k A ki−1d i
⇒ [adj( A )]ki p k d i = A A ki−1p k d i
r
r
r r
r r
⇒ [adj( A )] : [(a ∧ b) ⊗ d] = A A −1 : [(a ∧ b) ⊗ d]
(1.207)
Con lo cual concluimos que:
[adj(A)] = A A −1
A −1 =
⇒
1
[adj(A)] = 1 [cof(A)]T
A
A
(1.208)
Algunas consideraciones sobre la inversa de tensores:
ƒ
Si los tensores A y B son invertibles entonces las siguientes propiedades son
válidas:
( A ⋅ B) −1 = B −1 ⋅ A −1
(A )
−1 −1
=A
(1.209)
(βA )−1 = 1 A −1
β
det ( A ) = [det ( A )]
−1
−1
ƒ
La siguiente nomenclatura será utilizada para representar la transpuesta de la
inversa:
A −T ≡ ( A −1 ) T ≡ ( A T ) −1
(1.210)
Podemos demostrar que también es válida la relación adj( A ⋅ B) = adj(B) ⋅ adj( A ) ,
partiendo de la propia definición de la inversa (1.208):
B −1 ⋅ A −1 =
[adj(B)] ⋅ [adj(A)]
B
A
⇒ A B B −1 ⋅ A −1 = [adj(B)] ⋅ [adj( A )]
⇒ A B (A ⋅ B ) = [adj(B)] ⋅ [adj( A )]
−1
⇒AB
(1.211)
[adj(A ⋅ B)] = [adj(B)] ⋅ [adj(A)]
A ⋅B
⇒ adj( A ⋅ B) = [adj(B)] ⋅ [adj( A )]
donde hemos utilizado la propiedad que A ⋅ B = A B . Análogamente podemos demostrar
que cof( A ⋅ B) = [cof( A )] ⋅ [cof(B)] .
Inversa de una matriz
Pasos para obtener la inversa de una matriz A :
1) Obtener la matriz cofactor: cof (A ) .
Sea la matriz A :
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
 A 11
A = A 21
 A 31
A 12
A 22
55
A 13 
A 23 
A 33 
A 32
(1.212)
Definiremos la matriz M donde las componentes Mij serán obtenidas a partir del
determinante resultante de la matriz A al eliminar la línea i y la columna j , es decir:
 A 22

 A 32
A
M =  12
 A 32
 A 12

 A 22
A 23
A 33
A 13
A 21
A 31
A 11
A 23
A 33
A 13
A 21
A 31
A 11
A 22
A 32
A 12
A 33
A 13
A 31
A 11
A 33
A 13
A 23
A 21
A 23
A 31
A 11
A 21
A 32
A 12
A 22









(1.213)
con esto podemos definir la matriz cofactor de A :
cof (A ) = (−1) i + j Mij
(1.214)
2) Obtener la adjunta de la matriz A :
La adjunta de la matriz A es la transpuesta de la matriz cofactor:
adj(A ) = [cof (A )]
T
3) La inversa será:
A −1 =
luego se cumple que:
(1.215)
adj(A )
(1.216)
A
A [adj(A )] = A 1
(1.217)
donde 1 es la matriz identidad.
Teniendo en cuenta (1.64), podemos expresar las componentes de la primera, segunda,
tercera fila de la matriz cofactor, (1.214), respectivamente como: M1i =  ijk A 2 j A 3k ,
M 2i =  ijk A 1 j A 3k , M3i =  ijk A 1 j A 2 k .
r
r
Ejemplo 1.25: Dado un tensor A , demostrar que existe un vector no nulo n ≠ 0 tal que
r r
A ⋅ n = 0 si y solo si det ( A ) = 0 , Chadwick (1976).
Solución: Primero partimos del hecho que det ( A ) ≡ A = 0 y también escogemos una base
(
r r r
r r
r
)
arbitrario {f , g, h} , linealmente independiente luego f ⋅ g ∧ h ≠ 0 , y aplicando la definición
obtenida en (1.201):
(
[
)
r
r
r r r
r
f ⋅ g ∧ h A = ( A ⋅ f ) ⋅ ( A ⋅ g) ∧ ( A ⋅ h)
Por el hecho que det ( A ) ≡ A = 0 , eso implica que:
[
]
]
r
r
r
( A ⋅ f ) ⋅ ( A ⋅ g) ∧ ( A ⋅ h) = 0
r
r
r
Con lo cual concluimos que los vectores ( A ⋅ f ) , ( A ⋅ g) , ( A ⋅ h) son linealmente
dependientes. Esto implica que existen escalares no nulos α ≠ 0 , β ≠ 0 , γ ≠ 0 tal que:
r
r
r
r r
r
r
r r
r
α ( A ⋅ f ) + β ( A ⋅ g) + γ ( A ⋅ h) = 0 ⇒ A ⋅ αf + βg + γh = 0 ⇒
A ⋅n = 0
(
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
56
r
r
r
r
r r r
r
donde n = αf + βg + γh ≠ 0 , ya que {f , g, h} son linealmente independiente, ver Ejemplo
1.10.
r
r
r
Ahora escogemos dos vectores k , m que son linealmente independientes con n y
r r r
r r r
reemplazamos esta base {k , m, n} en lugar de los vectores {a, b, c} de la definición en
(1.201):
r r r
r
r
r
k ⋅ (m ∧ n) A = ( A ⋅ k ) ⋅ [( A ⋅ m) ∧ ( A ⋅ n)]
r r r
r r r
r r
Considerando que A ⋅ n = 0 y que k ⋅ (m ∧ n) ≠ 0 , ya que la base {k , m, n} está constituida
por vectores linealmente independientes, obtenemos que:
r r r
k ⋅ (m ∧ n) A = 0
14243
⇒
A =0
≠0
1.5.2.8
c.q.d.
Tensores Ortogonales (Transformación Ortogonal)
Tensores ortogonales juega un papel muy importante en la mecánica del continuo. Un
tensor de segundo orden ( Q ) se dice que es ortogonal cuando su transpuesta ( Q T ) es igual
a su inversa ( Q −1 ):
Q T = Q −1
(1.218)
Luego, se cumple que:
Q ⋅ QT = QT ⋅ Q = 1
Q ik Q jk = Q ki Q kj = δ ij
(1.219)
En notación indicial:
Q ⋅ QT
= (Q ik eˆ i ⊗ eˆ k ) ⋅ (Q jl eˆ l ⊗ eˆ j )
= Q ik Q jl δ kl (eˆ i ⊗ eˆ j )
= Q ik Q jk (eˆ i ⊗ eˆ j )
(1.220)
= δ ij (eˆ i ⊗ eˆ j )
Una transformación ortogonal propia tiene las siguientes características:
ƒ
La inversa de Q es igual a la transpuesta (ortogonalidad):
Q −1 = Q T
ƒ
(1.221)
El tensor Q será propio (tensores de rotación) si:
det (Q) ≡ Q = +1
(1.222)
Un tensor ortogonal es impropio cuando Q = −1 , tensores de rotación-reflexión. Podemos
demostrar que si A y B son tensores ortogonales, un tercer tensor resultante del producto
A ⋅ B = C también es un tensor ortogonal, ver Ejemplo 1.26.
r
r
Consideremos dos vectores arbitrarios a y b y que a través de una transformación
ortogonal obtenemos:
r
r
~
a = Q⋅a
;
r
r
~
b = Q ⋅b
(1.223)
r
r
~
~
El producto escalar de los vectores resultantes de esta operación ( a ) y ( b ) viene dado por:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
57
r r
r
r r r
r
r
~ ~
a ⋅ b = (Q ⋅ a) ⋅ (Q ⋅ b) = a ⋅ Q T ⋅ Q ⋅ b = a ⋅ b
123
=1
(1.224)
~~
ai b i = (Q ik a k )(Q ij b j ) = a k Q ik Q ij b j = a k b k
123
δ kj
r r
r r r
~ ~ ~2 r r r 2
~ ~
Lo que también es válido cuando a
= b , luego a ⋅ a = a = a ⋅ a = a . Con lo que
concluimos que una transformación ortogonal aplicada a vectores, preservan los módulos
de los vectores y preservan los ángulos entre los vectores, Figura 1.19. Es decir, una
transformación ortogonal está caracterizada sólo por rotaciones de los vectores.
Q
r
r
~
a = a
r
b
θ
r
~
b
θ
r
a
r
r
~
b = b
r
~
a
r r
~ ~ r r
a⋅b = a⋅b
Figura 1.19: Transformación ortogonal.
Ejemplo 1.26: Demostrar que si A y B son tensores ortogonales, el tensor resultante de
la operación C = A ⋅ B resulta ser otro tensor ortogonal.
Solución: C −1 = ( A ⋅ B) −1 = B −1 ⋅ A −1 = B T ⋅ A T = ( A ⋅ B) T = C T c.q.d.
1.5.2.9
Tensor Definido Positivo, Definido Negativo y Tensor SemiDefinido
Decimos que un tensor es definido positivo cuando se cumple que:
Notación Tensorial
r
r
x⋅T⋅x >0
r
para todo vector x no nulo.
Notación Indicial
Notación Matricial
x i Tij x j > 0
xT T x > 0
(1.225)
Decimos que un tensor es definido negativo cuando se cumple que:
Notación Tensorial
r
r
x⋅T⋅x <0
r
para todo vector x no nulo.
Notación Indicial
Notación Matricial
x i Tij x j < 0
xT T x < 0
r
r
r
(1.226)
r
El tensor será semi-definido positivo si x ⋅ T ⋅ x ≥ 0 para todo x ≠ 0 . Análogamente definimos
r
r
r r
un tensor semi-definido negativo cuando se cumple que x ⋅ T ⋅ x ≤ 0 , para todo x ≠ 0 .
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
58
r
r
r
r
Recordar que también se cumple que x ⋅ T ⋅ x = x ⋅ T sym ⋅ x , ver Ejemplo 1.16, luego si la
parte simétrica del tensor es definido positivo, el tensor también lo será.
r
r
r
r
r
Si α = x ⋅ T ⋅ x = T : ( x ⊗ x ) = Tij x i x j , luego la derivada de α con respecto a x viene dada
por:
∂x j
∂x i
∂α
x j + Tij x i
= Tij δ ik x j + Tij x i δ jk = Tkj x j + Tik x i = (Tki + Tik ) x i
= Tij
∂x k
∂x k
∂x k
(1.227)
Con lo que concluimos que:
r
∂α
r = 2 T sym ⋅ x
∂x
(1.228)
∂ 2α
r
r = 2 T sym
∂x ⊗ ∂x
(1.229)
y que:
NOTA: Como veremos más adelante, una condición necesaria y suficiente para que un
tensor sea definido positivo es que sus autovalores ( λ1 > 0 , λ 2 > 0 , λ 3 > 0 ) sean positivos.
La demostración se encuentra en el subapartado “Representación Espectral de un Tensor”.
■
Ejemplo 1.27: Sea un tensor de segundo orden arbitrario F . Demostrar que los tensores
resultantes C = F T ⋅ F y b = F ⋅ F T son tensores simétricos y semi-definidos positivos. Verificar
también en que condiciones C y b son tensores definidos positivos.
Solución:
C T = (F T ⋅ F )T = F T ⋅ (F T )T = F T ⋅ F = C
b T = (F ⋅ F T ) T = (F T )T ⋅ F T = F ⋅ F T = b
(simetría)
Con lo cual hemos demostrado que los tensores C = F T ⋅ F y b = F ⋅ F T son simétricos.
Para demostrar que los tensores C = F T ⋅ F y b = F ⋅ F T son semi-definidos positivos,
partimos de la definición de un tensor semi-definido positivo, es decir, un tensor A es
r
r
r r
semi-definido positivo si se cumple que x ⋅ A ⋅ x ≥ 0 , para todo x ≠ 0 . Luego:
r
r
r
r
x ⋅ C ⋅ x = x ⋅ (F T ⋅ F ) ⋅ x
r
r
= (F ⋅ x ) ⋅ (F ⋅ x )
r 2
= F ⋅x ≥0
En notación indicial:
x i C ij x j
= x i ( Fki Fkj ) x j
= ( Fki x i )( Fkj x j )
2
= Fki x i
≥0
r
r
r
r
x ⋅ b ⋅ x = x ⋅ (F ⋅ F T ) ⋅ x
r
r
= (F T ⋅ x ) ⋅ (F T ⋅ x )
r 2
= FT ⋅x ≥0
x i bij x j
= x i ( Fik F jk ) x j
= ( Fik x i )( F jk x j )
= Fik x i
2
≥0
Con lo cual demostramos que C = F T ⋅ F y b = F ⋅ F T son semi-definidos positivos.
r
r
r
Observemos que x ⋅ C ⋅ x = F ⋅ x
r
r
r
r
2
r
r
r
r
sólo será igual a cero, con x ≠ 0 , si F ⋅ x = 0 , y por
definición F ⋅ x = 0 con x ≠ 0 , si y solo si det ( F ) = 0 , ver Ejemplo 1.25. Luego, los
tensores C = F T ⋅ F y b = F ⋅ F T serán tensores definidos positivos si y solo si det ( F ) ≠ 0 .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
59
1.5.2.10 Descomposición Aditiva de Tensores
Dados dos tensores arbitrarios S , T ≠ 0 , y un escalar α , podemos hacer la representación
del tensor S a través de la siguiente descomposición aditiva de tensores:
S = αT + U
donde
U = S − αT
(1.230)
Observemos que dependiendo del valor de α tendremos infinitas posibilidades para la
representación del tensor S de forma aditiva de tensores. Pero, si
Tr ( T ⋅ UT ) = Tr (U ⋅ T T ) = 0 la descomposición aditiva es única. Partiendo de (1.230)
podemos obtener el valor de α :
S ⋅ T T = αT ⋅ T T + U ⋅ T T ⇒ Tr (S ⋅ T T ) = αTr ( T ⋅ T T ) + Tr (U ⋅ T T ) = αTr ( T ⋅ T T )
14243
=0
(1.231)
con lo cual obtenemos que:
α=
Tr (S ⋅ T T )
Tr ( T ⋅ T T )
(1.232)
Como ejemplo, supongamos que T = 1 , obtenemos α como:
α=
Tr (S ⋅ T T ) Tr (S ⋅ 1) Tr (S ) Tr (S )
=
=
=
3
Tr ( T ⋅ T T ) Tr (1 ⋅ 1) Tr (1)
(1.233)
Con eso podemos definir el tensor U como:
Tr (S )
1 ≡ S dev
3
(1.234)
Tr (S )
1 + S dev = S esf + S dev
3
(1.235)
U = S − αT = S −
Luego:
S=
NOTA: Al tensor S esf =
S dev = S −
Tr (S )
1 denominamos de tensor esférico y al tensor
3
Tr (S )
1 de tensor desviador de S . ■
3
1
2
Supongamos ahora que el tensor T = (S + S T ) luego, podemos definir α como:
[
]
1
Tr S ⋅ (S + S T ) T
Tr (S ⋅ T T )
2
=
α=
=1
Tr ( T ⋅ T T ) 1 Tr (S + S T ) ⋅ (S + S T ) T
4
[
]
(1.236)
donde hemos tenido en cuenta la propiedad de traza Tr[S ⋅ S ] = Tr[S T ⋅ S T ] ,
Tr[S T ⋅ S ] = Tr[S ⋅ S T ] . Con eso podemos definir el tensor U como:
U = S − αT = S −
1
1
(S + S T ) = (S − S T )
2
2
(1.237)
Representando así el tensor S a través de la siguiente descomposición aditiva única como:
S=
1
1
(S + S T ) + (S − S T ) = S sym + S anti
2
2
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.238)
Por: Eduardo W.V. Chaves
60
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
que es la misma obtenida en la descomposición aditiva de un tensor en una parte simétrica
y otra antisimétrica, ver expresión (1.151).
Ejemplo 1.28: Encontrar un tensor de cuarto orden P tal que se cumpla que:
P : A = A dev
Solución: Teniendo en cuenta la descomposición aditiva de un tensor en una parte esférica y
otra desviadora, podemos obtener que:
A = A esf + A dev =
Tr ( A )
1 + A dev
3
⇒
A dev = A −
Tr ( A )
1
3
Recurriendo a la definición de los tensores identidades de cuarto orden, definidos en
(1.176) y (1.174), donde se cumple que I : A = Tr ( A )1 y I : A = A . Entonces, podemos
decir que:
A dev = A −
Tr ( A )
1
1 
1



1 = I : A − I : A =  I − I  : A =  I − 1 ⊗ 1 : A
3
3
3 
3



Con lo cual, concluimos que:
1
P = I − 1 ⊗1
3
El tensor P es conocido como tensor proyección de cuarto orden, Holzapfel(2000).
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
1.5.3
61
Ley de Transformación de las Componentes de
Tensores
Las componentes de un tensor dependen del sistema de coordenadas, es decir, si cambia el
sistema de coordenadas debido a una rotación del sistema, las componentes también
cambiarán. Entre los sistemas de coordenadas, las componentes están relacionadas entre sí
a través de las leyes de transformación de base, Figura 1.20.
TENSORES
Interpretación matemática de conceptos físicos
(Independiente del sistema de coordenadas)
COMPONENTES
Representación del Tensor en
un Sistema de Coordenadas
SISTEMA DE
COORDENADAS
LEYES
I
TRANSFORMACIÓN
DE
SISTEMA DE
COORDENADAS
II
Figura 1.20: Leyes de transformación de base.
Consideremos el sistema de coordenadas cartesianas (x1 , x 2 , x3 ) representado por la base
r
ortonormal (eˆ 1 , eˆ 2 , eˆ 3 ) , véase Figura 1.21. En este sistema, un vector arbitrario v
representamos a través de sus componentes como sigue:
r
v = v i eˆ i = v 1 eˆ 1 + v 2 eˆ 2 + v 3 eˆ 3
(1.239)
Representaremos sus componentes a través de una matriz columna, i.e.:
 v1 
r
( v ) i = v i =  v 2 
 v 3 
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.240)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
62
x3
x 2′
γ1
x3′
x1′
ê′2
ê′3
ê3
ê1′
β1
x2
ê 2
ê1
α1
x1
Figura 1.21: Transformación de coordenadas.
Considerando ahora un nuevo sistema de coordenadas ortogonal (x1′ , x 2′ , x3′ ) , representado
r
por sus respectivos versores (eˆ 1′ , eˆ ′2 , eˆ ′3 ) , como se muestra en la Figura 1.21, el vector v
será representado en este sistema como v ′j eˆ ′j .
Como hemos mencionado anteriormente un vector, por ser un tensor, es independiente del
sistema adoptado, luego:
r
v = v ′k eˆ ′k = v j eˆ j
(1.241)
Para obtener las componentes según una dirección es suficiente hacer el producto escalar
por el versor correspondiente a esta dirección:
v ′k eˆ ′k ⋅ eˆ ′i = ( v j eˆ j ) ⋅ eˆ ′i
v ′k δ ki = ( v j eˆ j ) ⋅ eˆ ′i
(1.242)
v ′i = ( v 1 eˆ 1 + v 2 eˆ 2 + v 3 eˆ 3 ) ⋅ eˆ ′i
o aún:
 v 1′   ( v 1eˆ 1 + v 2 eˆ 2 + v 3 eˆ 3 ) ⋅ eˆ 1′ 
 v ′  = ( v eˆ + v eˆ + v eˆ ) ⋅ eˆ ′ 
2 2
3 3
2
 2  1 1
 v ′3   ( v 1 eˆ 1 + v 2 eˆ 2 + v 3 eˆ 3 ) ⋅ eˆ ′3 
(1.243)
Reestructurando la expresión anterior, obtenemos:
 v 1′   eˆ 1 ⋅ eˆ 1′
 v ′  = eˆ ⋅ eˆ ′
 2  1 2
 v ′3   eˆ 1 ⋅ eˆ ′3
eˆ 2 ⋅ eˆ 1′
eˆ 2 ⋅ eˆ ′2
eˆ 2 ⋅ eˆ ′3
eˆ 3 ⋅ eˆ 1′   v 1 

eˆ 3 ⋅ eˆ ′2   v 2 
eˆ 3 ⋅ eˆ ′3   v 3 
∴
a ij = eˆ j ⋅ eˆ ′i = eˆ ′i ⋅ eˆ j
(1.244)
o aún:
v ′i = a ij v j
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.245)
Por: Eduardo W.V. Chaves
1 TENSORES
63
donde definimos la matriz de transformación de coordenadas A ≡ aij como:
 eˆ 1 ⋅ eˆ 1′

A ≡ a ij = eˆ 1 ⋅ eˆ ′2
eˆ 1 ⋅ eˆ ′3

eˆ 2 ⋅ eˆ 1′
eˆ 2 ⋅ eˆ ′2
eˆ 2 ⋅ eˆ ′3
eˆ 3 ⋅ eˆ 1′   eˆ 1′ ⋅ eˆ 1
 
eˆ 3 ⋅ eˆ ′2  = eˆ ′2 ⋅ eˆ 1
eˆ 3 ⋅ eˆ ′3   eˆ ′3 ⋅ eˆ 1
eˆ 1′ ⋅ eˆ 2
eˆ ′2 ⋅ eˆ 2
eˆ ′3 ⋅ eˆ 2
eˆ 1′ ⋅ eˆ 3 

eˆ ′2 ⋅ eˆ 3 
eˆ ′3 ⋅ eˆ 3 
(1.246)
Considerando el producto escalar eˆ ′i ⋅ eˆ j = eˆ ′i eˆ j cos(xi′ , x j ) = cos(xi′ , x j ) , ver ecuación
(1.4), la relación anterior será expresada a través de los cosenos directores por:
 v 1′   cos( x1′ , x1 ) cos( x1′ , x 2 ) cos( x1′ , x3 )  v 1 
 v ′  = cos(x ′ , x ) cos(x ′ , x ) cos(x ′ , x )  v 
2
1
2
2
2
3   2
 2 
 v ′3   cos(x 3′ , x1 ) cos(x3′ , x 2 ) cos( x3′ , x 3 )  v 3 
{ 1444444424444444
3{
v′
(1.247)
v
A
v ′ = Av
En la Figura 1.21 se observa que, cos α 1 = cos(x1′ , x1 ) , cos β 1 = cos(x1′ , x 2 ) y
cos γ 1 = cos( x1′ , x3 ) , es decir, la primera fila de a ij esta formada por los cosenos de los
ángulos que forma x1′ con x1 , x 2 y x3 . Observemos que esta matriz es no simétrica
A ≠ A T , y será representada explícitamente por:
 a11
a ij ≡ A =  a 21
 a 31
a13 
a 23 
a33 
a12
a 22
a 32
(1.248)
La inversa de la ecuación (1.245) será:
v k eˆ k ⋅ eˆ i = v ′j eˆ ′j ⋅ eˆ i
v k δ ki = v ′j a ji
(1.249)
v i = v ′j a ji
También podemos decir que:
v = A T v′
eˆ i = a ji eˆ ′j
(1.250)
La inversa de la relación (1.247) viene dada por:
v = A −1v ′
(1.251)
Comparando las relaciones (1.251) y (1.249), concluimos que la matriz A es una matriz
ortogonal, es decir:
A −1 = A T
⇒
Notación
A T A = 1 Indicial

→ a ki a kj = δ ij
(1.252)
Tensor de segundo orden
Consideremos un sistema de coordenadas representado por su base ortonormal ê i luego,
el cambio de base para un nuevo sistema representado por su base ortonormal eˆ ′i será
dado por la ley de transformación: eˆ k = a ik eˆ ′i . Consideremos ahora la representación de
un tensor de segundo orden T de forma simbólica:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
64
T = Tkl eˆ k ⊗ eˆ l
= Tkl a ik eˆ ′i ⊗ a jl eˆ ′j
= Tkl a ik a jl eˆ ′i ⊗ eˆ ′j
= Tij′ eˆ ′i ⊗ eˆ ′j
(1.253)
Resultando que la ley de transformación para las componentes de tensores de segundo será:
Tij′ = Tkl a ik a jl
(1.254)
Tensor de tercer orden
Consideremos ahora un tensor de tercer orden S representado en la base ê i :
S = S lmn eˆ l ⊗ eˆ m ⊗ eˆ n
= S lmn ail eˆ ′i ⊗ a jm eˆ ′j ⊗ a kn eˆ ′k
= S lmn ail a jm a kn eˆ ′i ⊗ eˆ ′j ⊗ eˆ ′k
= S ′ijk eˆ ′i ⊗ eˆ ′j ⊗ eˆ ′k
(1.255)
concluyendo que las componentes del tensor de tercer orden en la nueva base eˆ ′i serán:
S ′ijk = S lmn a il a jm a kn
(1.256)
En forma general, las transformaciones de coordenadas de las componentes de tensores de
primer, segundo, tercer y cuarto orden serán dadas respectivamente por:
orden
a
de (x1 , x 2 , x3 ) →
(x1′ , x 2′ , x3′ )
a
de (x1′ , x 2′ , x3′ ) →
(x1 , x 2 , x3 )
0 (escalar)
1 (vector)
λ′ = λ
S i′ = a ij S j
λ = λ′
S i = a ji S ′j
2
S ij′ = a ik a jl S kl
S ij = a ki a lj S kl′
3
′ = a il a jm a kn S lmn
S ijk
′
S ijk = a li a mj a nk S lmn
4
′ = a im a jn a kp a lq S mnpq
S ijkl
′
S ijkl = a mi a nj a pk a ql S mnpq
(1.257)
Ejemplo 1.29: Obtener las componentes de la siguiente operación:
T′ = A ⋅ T ⋅ AT
donde Tij y a ij son las componentes de los tensores T y A , respectivamente.
Si a ij son las componentes de la matriz de transformación de base, hacer también la
representación de las componentes de los tensores T y T ′ en sus respectivos sistemas.
Solución: La expresión T ′ = A ⋅ T ⋅ A T en notación simbólica queda:
′ (eˆ a ⊗ eˆ b ) = a rs (eˆ r ⊗ eˆ s ) ⋅ T pq (eˆ p ⊗ eˆ q ) ⋅ a kl (eˆ l ⊗ eˆ k )
Tab
= a rs T pq a kl δ sp δ ql (eˆ r ⊗ eˆ k )
= a rp T pq a kq (eˆ r ⊗ eˆ k )
Para obtener las componentes de T ′ es suficiente hacer el doble producto escalar por la
base (eˆ i ⊗ eˆ j ) , resultando:
′ (eˆ a ⊗ eˆ b ) : (eˆ i ⊗ eˆ j ) = a rp T pq a kq (eˆ r ⊗ eˆ k ) : (eˆ i ⊗ eˆ j )
Tab
′ δ ai δ bj = a rp T pq a kq δ ri δ kj
Tab
Tij′ = a ip T pq a jq
Observemos que esta operación viene representada en forma matricial como:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
65
T ′ = A T AT
Si A es la matriz de transformación de base se cumple que A T = A −1 luego, se cumple
que T = A T T ′ A , y la representación de las componentes se muestran en la Figura abajo:
x3′
T ′ = A T AT
′
T33
′
T23
x3
x3′
T13′
T33
′
T31
T13
T23
x2′
T32
x1
T12′
′
T22
x2′
′
T21
T11′
T22
T31
T11
′
T32
T21
T12
x1′
x2
T = AT T ′ A
x1′
Figura 1.22: Ley de transformación de base.
r
r
NOTA: Aunque en la Figura 1.22 hemos dibujado los sistemas x y x ′ , en realidad estos
dos sistema tiene el mismo origen tal y como se puede apreciar en la Figura 1.21. Hemos
separado los sistemas para mejor visualización de las componentes. ■
Ejemplo 1.30: Considérese un tensor de segundo orden simétrico T = T T y I T , II T , III T
escalares dados por:
I T = Tr ( T ) = Tii
;
II T =
{
}
1
2
I T − Tr ( T 2 )
2
;
III T = det ( T )
Demostrar que I T , II T , III T son invariantes bajo un cambio de base.
Solución: a) Considerando la ley de transformación para un tensor de segundo orden dado
por (1.257), podemos decir que: Tij′ = a ik a jl Tkl . Luego, haciendo que i = j obtenemos Tii′
y vendrá dado por:
Tii′ = a ik a il Tkl = δ kl Tkl = Tkk = I T
Lo que demuestra que I T es un invariante.
b) Para demostrar que II T es un invariante es suficiente demostrar que Tr ( T 2 ) es un
invariante, ya que se demostró que I T es un invariante.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
66
Tr ( T ′ 2 ) = Tr ( T ′ ⋅ T ′) = T ′ : T ′ = Tij′ Tij′
= ( a ik a jl Tkl )( a ip a jq T pq )
= a ik a ip a jl a jq Tkl T pq
123 123
δ kp
δ lq
= T pl T pl
= T : T = Tr ( T T ⋅ T ) = Tr ( T ⋅ T ) = Tr ( T 2 )
c)
det ( T ′) = det ( T ′) = det (A T A T ) = det (A )det ( T )det (A T ) = det ( T )
1
424
3
1424
3
= ±1
= ±1
Consideremos ahora cuatro sistemas de coordenadas (x1 , x 2 , x3 ) , (x1′ , x 2′ , x3′ ) , (x1′′, x 2′′ , x3′′ ) y
(x1′′′, x 2′′′, x3′′′) y así como las siguientes matrices de transformación, ver Figura 1.23:
A : matriz de transformación del sistema (x1 , x 2 , x3 ) al sistema (x1′ , x 2′ , x3′ ) ;
B : matriz de transformación del sistema (x1′ , x 2′ , x3′ ) al sistema (x1′′, x 2′′ , x3′′ ) ;
C : matriz de transformación del sistema (x1′′, x 2′′ , x3′′ ) al sistema (x1′′′, x 2′′′, x3′′′) .
X′
A
−1
=A
B −1 = B T
T
B
A
BA
X
X ′′
AT BT
CBA
AT BT CT
C
X ′′′
C −1 = C T
Figura 1.23: Matrices de transformación entre sistemas.
Si consideramos una matriz columna v formada por las componentes del tensor de orden
r
uno v en el sistema (x1 , x 2 , x3 ) y las matrices de transformación A , B , C , podemos
decir que las componentes de este vector en el sistema (x1′ , x 2′ , x3′ ) serán:
y su forma inversa
v ′ = Av
(1.258)
v = AT v′
(1.259)
v ′′ = Bv ′
(1.260)
v ′ = B T v ′′
(1.261)
v ′′ = BA v
(1.262)
Las componentes de este vector en el sistema (x1′′, x ′2′ , x3′′ ) son:
y su forma inversa:
Reemplazando la ecuación (1.258) en la ecuación (1.260) hallamos:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
67
La matriz formada por BA será la matriz de transformación (también ortogonal, i.e.
(BA ) −1 = (BA ) T , ver Ejemplo 1.26) del sistema (x1 , x 2 , x3 ) para el sistema (x1′′, x 2′′ , x3′′ ) , ver
Figura 1.23. La forma inversa será obtenida reemplazando la ecuación (1.261) en la
ecuación (1.259), resultando:
v = A T B T v ′′
(1.263)
v = (BA ) v ′′ = (BA ) v ′′ = A T B T v ′′
(1.264)
Podríamos haber obtenido esta ecuación directamente de la ecuación (1.262)
−1
T
Análogamente, podemos obtener las componentes del vector en el sistema (x1′′′, x 2′′′, x3′′′) , ver
Figura 1.23, como:
v ′′′ = CBA v
1.5.3.1
Forma
 inversa
→
v = A T B T C T v ′′′
(1.265)
Transformada de Coordenadas en 2 Dimensiones
En el caso 2D tenemos como matriz de transformación de coordenadas una matriz con 4
componentes, donde dos son redundantes, y además las otras dos se pueden escribir en
función de una única variable libre, α .
y
y′
α y ′y = α
x′
α x′y
α y′y
α y ′x
π
−α
2
π
= +α
2
α x′y =
α y ′x
α x′x = α
x
Figura 1.24: Transformación de sistema de coordenadas- 2D.
La transformación de coordenadas entre el sistema x − y al sistema x ′ − y ′ viene dada por
la matriz A , que es:
 a11
A = a 21
 0
a12
a 22
0
0 cos(α x′x ) cos(α x′y ) 0
0 = cos(α y ′x ) cos(α y ′y ) 0
1  
0
0
1
(1.266)
cuya matriz A es la matriz con los cosenos directores, ver Figura 1.24. Por relaciones
trigonométricas podemos deducir que:
α x′x = α y′y ⇒ cos(α x′x ) = cos(α y′y ) = cos(α )
π

cos(α x′y ) = cos − α  = sin(α )
2

(1.267)
π

cos(α y′x ) = cos + α  = − sin(α )
2

Quedando la matriz de transformación (en 2D) definida por:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
68
 cos(α) sin(α ) 

− sin(α ) cos(α )
A=
(1.268)
Como comprobación de esta transformación consideremos un vector posición del punto
r
P dado por r , donde sus coordenadas son ( x P , y P ) en el sistema x − y , y las coordenadas
del mismo punto en el sistema x ′ − y ′ son ( x ′P , y ′P ) , ver Figura 1.25.
yP′
y
α
r
r
x ′P
β
y ′P
α
xP
xP
c
yP
α)
s(
co
y′
)
(α
sin
yP
yP
xP
P
x′
)
(α
is n
)
(α
s
o
x
Figura 1.25: Transformación de sistema de coordenadas- 2D.
Podemos escribir que:

π

x ′P = x P cos(α ) + y P cos − α 

′
 x P = x P cos(α ) + y P cos(β )
2





π

 y ′ = − x cos π − α  + y cos(α )
P
P
P
 y ′P = − x P cos(β ) + y P cos 2 − β 

 ⇒ 
2


 x ′P = x P cos(α ) + y P sin(α )
⇒
 y ′P = − x P sin(α) + y P cos(α )
(1.269)
(1.270)
En forma matricial:
 x   cos(α ) sin(α ) 
 x ′P   cos(α ) sin(α )   x P  Forma
Inversa
→ P  = 
 y ′  =  − sin(α ) cos(α )  y   

 P
 y P  − sin(α ) cos(α )
 P 
−1
 x ′P 
 y′ 
 P
(1.271)
Como la matriz es ortonormal, su inversa es igual a su transpuesta, es decir, A −1 = A T ,
luego la relación anterior puede ser reescrita como:
 x P  cos(α ) − sin(α )  x ′P 
 y  =  sin(α ) cos(α )   y ′ 
  P
 P 
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.272)
Por: Eduardo W.V. Chaves
1 TENSORES
69
Ejemplo 1.31: Encontrar la matriz de transformación del sistema ( x, y , z ) al sistema
x′′′, y ′′′, z ′′′ , ver Figura 1.26:
z = z′
z ′′ = z ′′′
β
y ′′′
y ′ = y ′′
γ
α
α
x
y
x′
γ
x ′′′
x ′′
Figura 1.26: Rotación.
Solución: Podemos observar que la obtención del sistema x′′′, y ′′′, z′′′ es una combinación de
rotaciones mostradas a continuación:
♦
Rotación según eje z
z = z′
sistema x, y , z para x′, y ′, z′
y′
α
α
x
x′
y
 cos α sin α 0
A = − sin α cos α 0
 0
0
1 
con 0 ≤ α ≤ 360 º
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
70
♦
Rotación según eje y′
z = z′
sistema x′, y ′, z′ para x′′, y ′′, z′′
z ′′
y ′ = y ′′
β
α
x
cos β 0 − sin β 
B =  0
1
0 
 sin β 0 cos β 
con 0 ≤ β ≤ 180 º
α
y
z = z′
z ′′
x′
x′
β
x ′′
♦
x ′′
Rotación según eje z ′′
z = z′
z ′′ = z ′′′
sistema x′′, y ′′, z′′ para x′′′, y ′′′, z′′′
β
y ′′′
y ′ = y ′′
γ
α
x
α
y
x′
 cos γ
C = − sin γ
 0
sin γ
cos γ
0
0
0 
1 
con 0 ≤ γ ≤ 360º
γ
x ′′′
x ′′
La matriz de transformación del sistema ( x, y , z ) para el sistema x′′′, y ′′′, z′′′ , ver Figura 1.23,
será dada por:
D = CBA
Resultando:
(sin α cos β cos γ + cos α sin γ ) − sin β cos γ 
 (cos α cos β cos γ − sin α sin γ )

D = (− cos α cos β sin γ − sin α cos γ ) (− sin α cos β sin γ + cos α cos γ ) sin β sin γ 


cos α sin β
sin α sin β
cos β
Los ángulos α, β , γ son conocidos como los ángulos de Euler.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
71
Ejemplo 1.32: Consideremos que las componentes de un tensor de segundo orden T , en
el sistema de referencia (x1 , x 2 , x 3 ) , están representadas por:
(T )ij
 3 − 1 0
= Tij = T =  − 1 3 0 
 0
0 1 
Sabiendo que la matriz de transformación de coordenadas del sistema (x1 , x 2 , x 3 ) al sistema
(x1′ , x 2′ , x 3′ ) viene dada por:


0 1
 0
 2

2
0
A=
2
 2



2
2
0
−
2
 2

Obtener las componentes del tensor Tij en el nuevo sistema de coordenadas (x1′ , x 2′ , x 3′ ) .
Solución: Como se definió en la ecuación (1.257), la ley de transformación para un tensor de
segundo orden es
Tij′ = aik a jl Tkl
Para que la operación anterior sea posible en forma matricial:
[ ]
Tij′ = [a i k ] [Tk l ] a l j
T
Luego:
 0

 2
T ′= 
 2

2
−
 2
T ′ = A T AT
0
2
2
2
2

1
0

3
1
0
−






0   − 1 3 0  0




0
0
1


1
0


2
2
2
2
0
−
2

2 
2 
2 

0 

Efectuando la operación de matrices obtenemos que:
1 0 0 
T ′ = 0 2 0 
0 0 4 
NOTA: Como podemos verificar en el ejemplo anterior las componentes del tensor T en
esta nueva base presenta una característica donde los términos fuera de la diagonal principal
son nulos. La pregunta ahora es: ¿Dado un tensor T , existe una transformación de base tal
que las componentes fuera de la diagonal principal de este tensor sean nulos? Este tipo de
problema es el denominado problema de autovalor y autovector. ■
1.5.4
Autovalores y Autovectores de un Tensor
Como hemos visto anteriormente, el producto escalar de un tensor de segundo orden T
con un vector (o un versor nˆ ′ ) resulta un vector, o dicho de otra manera, que la proyección
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
72
de un tensor de segundo orden según una dirección resulta un vector que no
necesariamente tiene la misma dirección de nˆ ′ , ver Figura 1.27 (a).
El problema de autovalor y autovector consiste en encontrar una dirección n̂ tal que el
vector proyección según está dirección esté coincidente con la dirección n̂ , ver Figura 1.27
(b).
b) Dirección principal de T .
a) Proyección de T sobre
un plano arbitrario.
r ˆ
t (n′) = T ⋅ nˆ ′
r ˆ
t (n) = T ⋅ nˆ
r ˆ
= t (n) nˆ
n̂
nˆ ′
= λnˆ
x3
n̂ - dirección principal
x2
λ - autovalor asociado a la
dirección n̂ .
x1
Figura 1.27: Proyección de un tensor sobre una dirección.
Luego, sea un tensor T . Un vector n̂ se dice autovector de T si existe un escalar λ ,
denominado autovalor, tal que:
T ⋅ nˆ = λnˆ
(1.273)
Si T es un tensor de segundo orden, podemos escribir la ecuación (1.273) en componentes
como:
Tij nˆ j = λnˆ i
⇒ Tij nˆ j − λnˆ i = 0 i
(
)
⇒ Tij − λδ ij nˆ j = 0 i
r
 → (T − λ1) ⋅ nˆ = 0
(1.274)
Notación
Tensorial
El conjunto de ecuaciones homogéneas anteriores solo tendrá soluciones no triviales de n̂
r
(es decir, para nˆ ≠ 0 ), ver Ejemplo 1.25, si y sólo si:
det ( T − λ1) = 0 ;
Tij − λδ ij = 0
(1.275)
que es conocido como el determinante característico del tensor T , explícitamente dado
por:
T11 − λ
T21
T12
T22 − λ
T13
T23
T31
T32
T33 − λ
=0
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.276)
Por: Eduardo W.V. Chaves
1 TENSORES
73
Desarrollando este determinante y reestructurando los términos podemos obtener el
polinomio característico, que está representado por una ecuación cúbica en λ :
λ3 − λ2 I T + λ II T − III T = 0
(1.277)
donde I T , II T , III T son los invariantes principales del tensor T , definidos en función de sus
componentes Tij por:
I T = Tr (T ) = Tii
II T
=
=
=
=
=
δ jk
1
( TrT ) 2 − Tr ( T 2 )
2
1
Tr ( Tij eˆ i ⊗ eˆ j ) Tr ( Tkl eˆ k ⊗ eˆ l ) − Tr Tij eˆ i ⊗ eˆ j ⋅ (Tkl eˆ k ⊗ eˆ l )
2
1
Tij δ ij Tkl δ kl − Tij Tkl δ jk Tr (eˆ i ⊗ eˆ l )
2
1
Tii Tkk − Tij Tkl δ jk δ il
2
1
Tii Tkk − Tij T ji = Mii = Tr[cof( T )]
2
[
{
{
{
{
]
[
}
}
[(
]}
]}
)
(1.278)
III T = det ( T ) = Tij =  ijk Ti1 T j 2 Tk 3
donde Mii es la traza de la matriz cofactor definida en la expresión (1.213), i.e.
Mii = M11 + M 22 + M33 . Explícitamente, los invariantes vienen dados por:
IT
II T
III T
= T11 + T22 + T33
T22 T23
T11 T13
T
T12
=
+
+ 11
T32 T33 T31 T33 T21 T22
= T22 T33 − T23 T32 + T11 T33 − T13 T31 + T11 T22 − T12 T21
= T11 ( T22 T33 − T32 T23 ) − T12 (T21 T33 − T31 T23 ) + T13 ( T21 T32 − T31 T22 )
(1.279)
Si T es un tensor simétrico, los invariantes principales se resumen de la forma:
IT
= T11 + T22 + T33
II T
III T
2
= T11 T22 + T11 T33 + T22 T33 − T122 − T132 − T23
2
= T11 T22 T33 + T12 T13 T23 + T13 T12 T23 − T122 T33 − T23
T11 − T132 T22
(1.280)
OBS.: Encontrar los autovalores (también conocidos como valores principales) es
equivalente a encontrar unas direcciones principales (autovectores) tal que Tij = 0
para i ≠ j . Además podemos decir que los autovectores constituyen una matriz de
transformación entre el sistema original y el sistema formado por los autovectores.
Los autovalores λ1 , λ 2 , λ 3 se obtienen al resolver la ecuación cúbica (1.277). Una vez
obtenidos los autovalores, los autovectores se obtienen al aplicar la ecuación (1.274), i.e.
( Tij − λ 1δ ij ) nˆ (j1) = 0 i , ( Tij − λ 2 δ ij ) nˆ (j2 ) = 0 i , ( Tij − λ 3 δ ij ) nˆ (j3) = 0 i , con la restricción
nˆ k nˆ k = 1 . Estos autovectores constituyen una nueva base denominada de espacio principal.
Si T es simétrico, el espacio principal viene definido por una base ortonormal y los
autovalores son todos reales. Si los tres autovalores son distintos λ 1 ≠ λ 2 ≠ λ 3 tenemos tres
direcciones principales únicas. Si dos autovalores son iguales, e.g. λ 1 = λ 2 ≠ λ 3 tenemos en
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
74
este caso una dirección principal única ( n̂ (3) ) correspondiente al autovalor λ 3 y las otras
dos pueden ser cualesquiera mientras sean mutuamente ortogonales entre si y a n̂ (3) , es
decir, cualquier dirección que este en el plano normal a n̂ (3) . Si λ 1 = λ 2 = λ 3 cualquier
dirección será una dirección principal. Cuando un tensor presenta los tres autovalores
iguales lo denominamos de Tensor Esférico, ver A.4 Elipsoide del Tensor.
Una vez obtenidos los autovectores, estos constituyen una base ortonormal denominado
de espacio principal. En este espacio sólo tendremos componentes normales. Luego, las
componentes del tensor en este espacio vienen representadas por:
λ 1
′
Tij =  0
 0
0
λ2
0
  T1
=0
 
λ 2   0
0
0
0
T2
0
0
0 
T3 
(1.281)
En este espacio (espacio principal), los invariantes pueden ser obtenidos como:
IT
= T1 + T2 + T3
II T
III T
= T1 T2 + T2 T3 + T1 T3
= T1 T2 T3
(1.282)
Cuyos valores tienen que coincidir con los valores obtenidos en (1.279), ya que son
invariantes. En el caso particular que el tensor sea esférico, es decir, T1 = T2 = T3 = T , se
cumple que I T2 = 3 II T , III T = T 3 .
Dado un tensor antisimétrico W , los invariantes principales vienen dados por:
IW
II W
= Tr (W ) = 0
− Tr (W 2 )
1
= ( TrW ) 2 − Tr (W 2 ) =
2
2
0
0
W23
W13
0
=
+
+
− W23
0
− W13
0
− W12
[
]
W12
0
(1.283)
= W23 W23 + W13 W13 + W12 W12
III W
= ω2
=0
r
r r
donde ω 2 = w = w ⋅ w = W232 + W132 + W122 , ver expresión (1.133). Luego, la ecuación
característica correspondiente a un tensor antisimétrico queda:
2
λ3 − λ2 I W + λ II W − III W = 0
⇒ λ3 + ω 2 λ = 0
(
(1.284)
)
⇒ λ λ2 + ω 2 = 0
Con lo cual comprobamos que por lo menos un autovalor es real e igual a cero, y dos
posibles raíces imaginarias:
λ2 + ω 2 = 0
1.5.4.1
⇒
λ2 = −ω 2 = 0
⇒
λ (1, 2 ) = ±ω − 1 = ±ω i
(1.285)
Ortogonalidad de los Autovectores
Retomando la definición de autovalores dada por (1.273), si λ 1 , λ 2 , λ 3 (con λ 1 ≠ λ 2 ≠ λ 3 )
son los autovalores del tensor de segundo orden T luego, se cumple que:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
T ⋅ nˆ (1) = λ 1nˆ (1)
;
75
T ⋅ nˆ ( 2 ) = λ 2 nˆ ( 2)
T ⋅ nˆ (3) = λ 3 nˆ (3)
(1.286)
Podemos multiplicar la primera expresión por n̂ ( 2) y a la segunda por n̂ (1) resultando:
nˆ ( 2 ) ⋅ T ⋅ nˆ (1) = λ 1nˆ ( 2 ) ⋅ nˆ (1)
;
nˆ (1) ⋅ T ⋅ nˆ ( 2 ) = λ 2 nˆ (1) ⋅ nˆ ( 2 )
(1.287)
Considerando T simétrico, se cumple que nˆ ( 2) ⋅ T ⋅ nˆ (1) = nˆ (1) ⋅ T T ⋅ nˆ ( 2) = nˆ (1) ⋅ T ⋅ nˆ ( 2)
luego:
λ 1nˆ ( 2) ⋅ nˆ (1) = λ 2 nˆ (1) ⋅ nˆ ( 2 )
(1.288)
Teniendo en cuenta que nˆ ( 2) ⋅ nˆ (1) = nˆ (1) ⋅ nˆ ( 2) , la relación anterior queda:
(λ 1 − λ 2 ) nˆ (1) ⋅ nˆ ( 2) = 0
(1.289)
Ya que λ1 ≠ λ 2 ≠ 0 , para satisfacer (1.289) se debe cumplir que:
nˆ (1) ⋅ nˆ ( 2 ) = 0
(1.290)
Análogamente podemos demostrar que nˆ (1) ⋅ nˆ (3) = 0 y nˆ ( 2) ⋅ nˆ (3) = 0 . Con lo que
demostramos que los autovectores son versores ortogonales entre sí, constituyendo así una
base ortonormal, ver Figura 1.28, donde la matriz de transformación de base viene dada
por:
 nˆ (1)   nˆ 1(1)

 
A = nˆ ( 2)  = nˆ 1( 2)
nˆ (3)  nˆ (3)

  1
nˆ (21)
nˆ (22 )
nˆ (23)
nˆ 3(1) 

nˆ 3( 2 ) 
nˆ (33) 
(1.291)
NOTA: Si el tensor no es simétrico, los autovectores no necesariamente constituyen una
base ortonormal.
diagonalización
T ′ = A T AT
x3
T33
T2
n̂
( 3)
n̂( 2 )
x 2′
T23
T13
n̂(1)
T22
T12
x1
x3′
T23
T13
T11
T3
T12
T1
x2
x1′
T = AT T ′ A
Espacio Principal
Figura 1.28: Diagonalización.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
76
Ejemplo 1.33: Demostrar que las siguientes relaciones son invariantes:
C12 + C 22 + C 32
; C13 + C 23 + C 33
;
C14 + C 24 + C 34
donde C1 , C 2 , C 3 son los autovalores del tensor de segundo orden C .
Solución :
Cualquier combinación de los invariantes principales será un invariante. Intentaremos
expresar las relaciones anteriores en función de los invariantes principales.
Consideremos la siguiente relación:
(
)
I C2 = (C1 + C 2 + C 3 ) = C12 + C 22 + C 32 + 2 C1 C 2 + C1 C 3 + C 2 C 3
1444424444
3
2
II C
⇒ C12 + C 22 + C 32 = I C2 − 2 II C
Comprobando que C12 + C 22 + C 32 es un invariante. Análogamente, podemos obtener que:
C13 + C 23 + C 33 = I C3 − 3 II C I C + 3 III C
C14 + C 24 + C 34 = I C4 − 4 II C I C2 + 4 III C I C + 2 II C2
Ejemplo 1.34: Demostrar que si Q es un tensor de segundo orden ortogonal propio, y E
es un tensor de segundo orden, los autovalores de E no cambian con la transformación:
E* = Q ⋅ E ⋅ QT
Solución:
Los autovalores ( λ i ) del tensor E obtenemos a partir del determinante característico:
0 = det (E *ij − λδ ij )
0 = det (E * − λ* 1 * ) = det (E * − λ1)
(
)
= det (Q ⋅ E ⋅ Q − Q ⋅ λ1 ⋅ Q )
= det [Q ⋅ (E − λ1 ) ⋅ Q ]
(3) det (E − λ1) det
(Q3)
= det
12Q
1
424
= det Q ⋅ E ⋅ Q T − λ1
T
T
T
T
1
1
= det (E − λ1 )
(
= det (Q E
= det [Q (E
= det Q ik E kp Q jp − λδ ij
ik
)
− λQ ik Q jp δ kp
kp Q jp
)
) ]
= det (Q )det (E − λδ ) det (Q )
= det (E − λδ )
ik
kp
− λδ kp Q jp
ik
kp
kp
jp
kp
kp
*
Con lo cual comprobamos que E y E tienen los mismos autovalores.
1.5.4.2
Solución de la Ecuación Cúbica
Si un tensor T es simétrico podemos demostrar que las raíces de la ecuación característica
( λ3 − λ2 I T + λ II T − III T = 0 ) serán todas raíces reales, definidas de la forma:
  α  I
λ 1 = 2 S cos   + T
  3  3
  α 2π   I T
λ 2 = 2 S cos +
 +
3  3
 3
(1.292)
  α 4π   I T
λ 3 = 2S cos +
 +
3   3
 3
con
R=
I T2 − 3 II T
;
3
S=
R
;
3
Q=
I T II T
2I 3
− III T − T ;
3
27
T=
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
R3
;
27
 Q 

 2T 
α = arccos −
Por: Eduardo W.V. Chaves
1 TENSORES
77
con α en radianes.
(1.293)
Ya que λ1 , λ 2 , λ 3 son los autovalores del tensor T , luego podemos reestructurar la
solución como:
λ 1
0

 0
0
λ2
0

 α
0
0

cos 3 
0
1 0 0

  
IT 
 α 2π 




0=
0 1 0 + 2 S
0
cos +
0




3
3 
3
0 0 1


λ 3 
 α 4π  
144244
3
 0
0
cos
+


Parte Esférica

 344343
 
14
4444444244444
(1.294)
Parte Desviadora
donde distinguimos claramente la parte esférica y desviadora del tensor. Observemos que si
T es esférico se cumple que I T2 = 3 II T , luego R = S = 0 .
Ejemplo 1.35: Determinar los valores principales y las direcciones principales del tensor de
segundo orden simétrico T , cuyas componentes en la base Cartesiana se representan
matricialmente por:
 3 − 1 0
(T )ij = Tij = T = − 1 3 0
 0
0 1 
Solución: Buscamos soluciones no triviales para Tij − λδ ij n j = 0 i , con la restricción de que
(
)
nˆ j nˆ j = 1 . Como ya hemos visto, la solución no trivial requiere la condición:
Tij − λδ ij = 0
Explícitamente, la expresión anterior queda:
T11 − λ
T21
T12
T22 − λ
T13
T23
3 − λ −1
= −1 3 − λ
T31
T32
T33 − λ
0
0
0
0
=0
1− λ
Desarrollando el determinante anterior obtenemos la ecuación cúbica:
[
]
(1 − λ ) (3 − λ ) 2 − 1 = 0
3
2
λ − 7 λ + 14λ − 8 = 0
Podríamos haber obtenido directamente la ecuación característica anterior a través de los
invariantes:
I T = Tr ( Tij ) = Tii = T11 + T22 + T33 = 7
II T =
T
1
Tii T jj − Tij Tij = 22
T32
2
(
)
T23
T33
+
T11
T13
T31
T33
+
T11
T12
T21
T22
= 14
III T = Tij =  ijk Ti1 T j 2 Tk 3 = 8
Luego, utilizando la ecuación (1.277), la ecuación característica será:
λ3 − λ2 I T + λ II T − III T = 0
→
λ3 − 7λ2 + 14λ − 8 = 0
Resolviendo la ecuación cúbica podemos obtener las tres raíces reales, puesto que la matriz
T es simétrica:
λ 1 = 1;
λ 2 = 2;
λ3 = 4
Podemos además comprobar si los invariantes están bien calculados utilizando la expresión
de los invariantes en función de los autovalores:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
78
I T = λ1 + λ 2 + λ 3 = 1 + 2 + 4 = 7 ✓
II T = λ 1 λ 2 + λ 2 λ 3 + λ 3 λ 1 = 1 × 2 + 2 × 4 + 4 × 1 = 14 ✓
III T = λ 1 λ 2 λ 3 = 8 ✓
Con lo que podemos comprobar que los invariantes son los mismos que los obtenidos
anteriormente.
Cálculo de las direcciones principales:
Para obtener las direcciones principales, utilizamos la ecuación (1.274), donde cada
autovalor λ i está asociado a un autovector nˆ (i ) .
Para λ 1 = 1
3 − λ 1
 −1

 0
−1
3 − λ1
0
0   n1   0 
0   n 1  3 − 1 − 1




0  n 2  =  − 1 3 − 1 0  n 2  = 0 
0 1 − 1 n 3  0 
1 − λ 1  n 3   0
resultando el siguiente sistema de ecuaciones:
2n1 − n 2 = 0 

 ⇒ n1 = n 2 = 0
 − n1 + 2n 2 = 0
0n = 0
 3
n i n i = n12 + n 22 + n 32 = 1
Luego, podemos obtener que: λ1 = 1 ⇒ nˆ i(1) = [0 0 ± 1] .
NOTA: Esta solución podría haberse determinado previamente por la situación particular
que presentan las componentes del tensor. Al ser los términos T13 = T23 = T31 = T32 = 0 ,
T33 = 1 ya es un valor principal, como consecuencia esta dirección ya es una dirección
principal. ■
Para λ 2 = 2
−1
0   n 1  3 − 2 − 1
0   n1   0 
3 − λ 2
 −1




3 − λ2
0  n 2  =  − 1 3 − 2
0  n 2  = 0 

 0
0
1 − λ 2  n 3   0
0
1 − 2  n 3  0 
n1 − n 2 = 0 ⇒ n1 = n 2

 − n1 + n 2 = 0
− n = 0
 3
Podemos observar que las dos primeras ecuaciones son linealmente dependientes.
Necesitamos entonces de una ecuación adicional:
n i n i = n12 + n 22 + n 32 = 1 ⇒ 2n12 = 1 ⇒ n1 = ±
1
2
Luego:
λ2 = 2
⇒

1
nˆ i( 2 ) =  ±
2

±
1
2

0

Para λ 3 = 4
3 − λ 3
 −1

 0
−1
3 − λ3
0
0   n1  0 
0   n 1  3 − 4 − 1




0  n 2  = 0 
0  n 2  =  − 1 3 − 4
0
1 − 4  n 3  0 
1 − λ 3  n 3   0
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
79
 − n1 − n 2 = 0 

 ⇒ n1 = −n 2
 − n1 − n 2 = 0 
− 3n = 0
3

1
2
n i n i = n12 + n 22 + n 32 = 1 ⇒ 2n 22 = 1 ⇒ n 2 = ±
Resultando:
λ3 = 4
⇒

nˆ i(3) =  m

1
2
±

0

1
2
Podemos entonces resumir que las direcciones principales correspondientes a sus valores
principales son:
λ1 = 1
⇒ nˆ (i1)
= [0 0 ± 1]
λ2 = 2
⇒ nˆ (i 2 )

= ±

1
2
±
1
2

0

λ3 = 4
⇒ nˆ (i 3)

= m

1
2
±
1
2

0

NOTA: Las componentes del tensor en el sistema de coordenadas original (x1 , x 2 , x 3 ) es el
mismo del Ejemplo 1.32. Los autovalores obtenidos fueron λ 1 = 1 , λ 2 = 2 y λ 3 = 4 y la
matriz de transformación A está constituida por los autovectores de T . Verificando así
que los autovectores constituyen una base de transformación del sistema (x1 , x 2 , x 3 ) para el
sistema (x1′ , x 2′ , x 3′ ) que está formada por los ejes principales ■
1.5.5
Representación Espectral de Tensores
De la solución de la ecuación (1.277) obtenemos tres autovalores: λ 1 ≡ T1 , λ 2 ≡ T2 ,
λ 3 ≡ T3 . Cada autovalor estará asociado a un autovector, es decir:
[
= [ nˆ
= [ nˆ
para T1
⇒ nˆ i(1)
= nˆ 1(1)
para T2
⇒ nˆ i( 2 )
para T3
⇒ nˆ i(3)
]
nˆ (21)
nˆ (31)
( 2)
1
nˆ (22 )
nˆ 3( 2 )
( 3)
1
nˆ (23)
nˆ 3(3)
]
]
(1.295)
En el espacio principal, cuyas bases están formadas por los autovectores nˆ (1) , nˆ ( 2) , nˆ (3) , el
tensor T tendrá como componentes una matriz diagonal formada por los autovalores:
 T1
Tij′ = T ′ =  0
 0
0
T2
0
0
0 
T3 
(1.296)
Sabiendo que los autovectores forman una base de transformación tal que:
luego, la forma inversa será:
T ′ = A T AT
(1.297)
T = AT T ′ A
(1.298)
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
80
donde
 nˆ (1)   nˆ 1(1)

 
A = nˆ ( 2)  = nˆ 1( 2)
nˆ (3)  nˆ (3)

  1
nˆ 3(1) 

nˆ 3( 2 ) 
nˆ (33) 
nˆ (21)
nˆ (22 )
nˆ (23)
(1.299)
Explícitamente, la relación (1.298) queda:
 T11
T
 12
 T13
T12
T22
T23
nˆ 1(1) nˆ 1( 2 )
T13 

T23  = nˆ (21) nˆ (22 )
nˆ (1) nˆ ( 2 )
T33 
3
 3
T
 1 0
T 
= A  0 T2
 0 0
nˆ 1(3)   T1

nˆ (23)   0
nˆ 3(3)   0
0
0  A
T3 
0
T2
0
0   nˆ 1(1)

0  nˆ 1( 2)
T3  nˆ 1(3)
nˆ (21)
nˆ (22 )
nˆ (23)
nˆ (31) 

nˆ 3( 2) 
nˆ 3(3) 
(1.300)
1 0 0
0 0 0 
0 0 0 



T 
T 
= T1A 0 0 0 A + T2 A 0 1 0A + T3 A 0 0 0 A
0 0 0
0 0 0
0 0 1
T
donde se cumple que:
nˆ 1(1) nˆ 1(1)
1 0 0

A T 0 0 0A = nˆ (21) nˆ 1(1)
nˆ (1) nˆ (1)
0 0 0
 3 1
nˆ 1(1) nˆ (21)
nˆ (21) nˆ (21)
nˆ 3(1) nˆ (21)
nˆ 1( 2 ) nˆ 1( 2 )
0 0 0 

A T 0 1 0A = nˆ (22) nˆ 1( 2)
nˆ ( 2 ) nˆ ( 2 )
0 0 0
 3 1
nˆ 1( 2 ) nˆ (22 )
nˆ (22 ) nˆ (22 )
nˆ 3( 2 ) nˆ (22 )
nˆ 1(3) nˆ 1(3)
0 0 0 

A T 0 0 0A = nˆ (23) nˆ 1(3)
nˆ (3) nˆ (3)
0 0 1
 3 1
nˆ 1(3) nˆ (23)
nˆ (23) nˆ (23)
nˆ (33) nˆ (23)
nˆ 1(1) nˆ 3(1) 

nˆ (21) nˆ 3(1)  = nˆ i(1) nˆ (j1)
nˆ 3(1) nˆ 3(1) 
nˆ 1( 2 ) nˆ (32 ) 

nˆ (22 ) nˆ (32 )  = nˆ i( 2 ) nˆ (j2 )
nˆ (32 ) nˆ (32 ) 
nˆ 1(3) nˆ 3(3) 

nˆ (23) nˆ 3(3)  = nˆ i(3) nˆ (j3)
nˆ 3(3) nˆ 3(3) 
(1.301)
Luego, podemos representar las componentes de un tensor de segundo orden en función
de sus valores principales y autovectores como:
Tij = T1 nˆ i(1) nˆ (j1) + T2 nˆ (i 2 ) nˆ (j2 ) + T3 nˆ (i 3) nˆ (j3)
(1.302)
o en notación tensorial como:
T = T1 nˆ (1) ⊗ nˆ (1) + T2 nˆ ( 2 ) ⊗ nˆ ( 2 ) + T3 nˆ (3) ⊗ nˆ (3)
(1.303)
o también
T=
3
∑T
a =1
a
nˆ ( a ) ⊗ nˆ ( a )
Representación espectral de un
tensor simétrico de segundo orden
(1.304)
que es la denominada representación espectral del tensor. Observemos que en la expresión
anterior tenemos que recurrir al símbolo de suma ya que el índice aparece tres veces en la
expresión.
NOTA: La representación espectral (1.304) podría haber sido obtenida fácilmente
partiendo de la definición del tensor identidad (tensor esférico) dada por (1.169),
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
81
1 = nˆ i ⊗ nˆ i , donde {nˆ 1 , nˆ 2 , nˆ 3 } constituye una base ortonormal. Podemos también
3
representar 1 = nˆ i ⊗ nˆ i a través del símbolo de suma como 1 = ∑ nˆ ( a ) ⊗ nˆ ( a ) . Luego, se
a =1
cumple que:
 3

T = T ⋅ 1 = T ⋅  nˆ ( a ) ⊗ nˆ ( a )  =
 a =1

∑
3
∑
T ⋅ nˆ ( a ) ⊗ nˆ ( a ) =
a =1
3
∑T
a
nˆ ( a ) ⊗ nˆ ( a )
(1.305)
a =1
donde hemos utilizado la definición de autovalor y autovector T ⋅ nˆ ( a ) = Ta nˆ ( a ) . ■
Consideremos un tensor ortogonal R cuya transformación ortogonal aplicada al versor
ˆ . Podemos entonces hacer la
original N̂ transforma en el versor n̂ , es decir, nˆ = R ⋅ N
representación espectral de un tensor ortogonal como:
 3 ˆ (a) ˆ (a) 
⊗ N  =
R = R ⋅ 1 = R ⋅  N
 a =1

∑
3
∑
ˆ (a) ⊗ N
ˆ (a ) =
R ⋅N
a =1
3
∑ nˆ
(a )
ˆ (a)
⊗N
(1.306)
a =1
En el espacio de las direcciones principales, la potencia de tensores podemos expresarla
como:
 T1n

= 0
0

(T )
n
ij
0
T2n
0
0

0
T3n 
(1.307)
Luego, la representación espectral del tensor T n será:
3
∑T
Tn =
n
a
nˆ ( a ) ⊗ nˆ ( a )
(1.308)
a =1
Si ahora queremos calcular la raíz cuadrada del tensor T , podemos fácilmente obtener a
través de la representación espectral:
T=
3
∑
Ta nˆ ( a ) ⊗ nˆ ( a )
(1.309)
a =1
r
r
Consideremos un tensor semi-definido positivo ( T ), luego hay que cumplir x ⋅ T ⋅ x ≥ 0
r r
para todo x ≠ 0 . Aplicando la representación espectral obtenemos que:
r
r
x⋅T⋅x ≥0
 r
r  3
⇒ x ⋅  Ta nˆ ( a ) ⊗ nˆ ( a )  ⋅ x ≥ 0
 a =1

3
r
r
⇒
Ta x ⋅ nˆ ( a ) ⊗ nˆ ( a ) ⋅ x ≥ 0
∑
(1.310)
∑
a =1
r
Observemos que el resultado de la operación ( x ⋅ nˆ (a ) ) es un escalar con lo cual podemos
escribir que:
3
∑
a =1
r
r
Ta x ⋅ nˆ ( a ) ⊗ nˆ ( a ) ⋅ x ≥ 0
⇒
r
( x ⋅ nˆ ) ]
∑ T [1
4243
3
a
a =1
(a) 2
>0
r
r
r
⇒ T1 ( x ⋅ nˆ (1) ) 2 + T2 ( x ⋅ nˆ ( 2 ) ) 2 + T3 ( x ⋅ nˆ (3) ) 2 ≥ 0
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.311)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
82
r
r
r
Fijemos que la expresión anterior hay que cumplir para todo x ≠ 0 . Si adoptamos x = n̂ (1)
quedamos con T1 (nˆ (1) ⋅ nˆ (1) ) 2 = T1 ≥ 0 , análogamente para T 2 y T 3 . Con lo cual
demostramos que si un tensor es semi-definido positivo eso implica que sus autovalores
son mayores o igual a cero, T 1 ≥ 0 , T 2 ≥ 0 , T 3 ≥ 0 . Concluimos también que, un tensor será
definido positivo si y solo si sus autovalores son positivos y distintos de cero, es decir,
T 1 > 0 , T 2 > 0 , T 3 > 0 . Como consecuencia la traza de un tensor definido positivo es mayor
que cero. Si la traza de un tensor definido positivo es igual a cero, eso implica que el tensor
es el tensor nulo.
Teniendo en cuenta lo expuesto anteriormente, queda trivial la representación de los
tensores identidades de cuarto orden de la siguiente forma:
I = δ ik δ jl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l = eˆ i ⊗ eˆ j ⊗ eˆ i ⊗ eˆ j =
3
3
∑∑ eˆ
a
⊗ eˆ b ⊗ eˆ a ⊗ eˆ b
(1.312)
a =1 b =1
Luego, como I es un tensor isótropo, será válido también en cualquier base ortonormal
nˆ ( a ) :
I=
3
∑ nˆ
(a)
⊗ nˆ (b ) ⊗ nˆ ( a ) ⊗ nˆ (b )
(1.313)
a ,b =1
Análogamente, podemos hacer la representación de los tensores I , I como:
I = δ il δ jk eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l = eˆ i ⊗ eˆ j ⊗ eˆ j ⊗ eˆ i
I=
3
∑ nˆ
(a)
(1.314)
⊗ nˆ (b ) ⊗ nˆ (b ) ⊗ nˆ ( a )
(1.315)
a ,b =1
y
I = δ ij δ kl eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l = eˆ i ⊗ eˆ i ⊗ eˆ k ⊗ eˆ k
I=
3
∑ nˆ
(a)
(1.316)
⊗ nˆ ( a ) ⊗ nˆ (b ) ⊗ nˆ (b )
(1.317)
a ,b =1
Ejemplo 1.36: Sea w un tensor antisimétrico de segundo orden y V un tensor de
segundo orden definido positivo cuya representación espectral viene dada por:
V=
3
∑λ
a
nˆ ( a ) ⊗ nˆ ( a )
a =1
w puede ser representado por:
3
w = ∑ w ab nˆ (a ) ⊗ nˆ (b)
Demostrar que el tensor antisimétrico
a ,b =1
a ≠b
Demostrar también que se cumple la relación:
3
w ⋅ V − V ⋅ w = ∑ w ab (λ b − λ a ) nˆ ( a ) ⊗ nˆ (b)
a ,b =1
a ≠b
Solución:
Es cierto que
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES

83

3
3

a =1
a =1
w ⋅ 1 = w ⋅  ∑ nˆ ( a ) ⊗ nˆ ( a)  = ∑ w ⋅ nˆ (a ) ⊗ nˆ (a ) = ∑ (wr ∧ nˆ ( a) ) ⊗ nˆ ( a)
3
 a =1
∑ w (nˆ
3
=
b
(b )
)
∧ nˆ ( a ) ⊗ nˆ ( a )
a ,b =1
r
r
donde hemos aplicado la propiedad de un tensor antisimétrico w ⋅ nˆ = w ∧ nˆ , donde w es
el vector axil asociado al tensor w . Expandiendo la expresión anterior obtenemos que
w = wb (nˆ (b) ∧ nˆ (1) ) ⊗ nˆ (1) + wb (nˆ (b) ∧ nˆ ( 2) ) ⊗ nˆ ( 2) + wb (nˆ (b) ∧ nˆ (3) ) ⊗ nˆ (3) =
(
+ w (nˆ
+ w (nˆ
)
(
)
(
)
= w1 nˆ (1) ∧ nˆ (1) ⊗ nˆ (1) + w2 nˆ ( 2) ∧ nˆ (1) ⊗ nˆ (1) + w3 nˆ (3) ∧ nˆ (1) ⊗ nˆ (1) +
1
1
(1)
∧ nˆ
(2)
(1)
∧ nˆ
( 3)
) ⊗ nˆ
) ⊗ nˆ
( 3)
(
(nˆ
+ w2 nˆ
(2)
+ w2
( 2)
∧ nˆ
( 2)
∧ nˆ
( 2)
( 3)
Simplificando la expresión anterior resulta que:
) ⊗ nˆ
) ⊗ nˆ
( 2)
( 3)
(
(nˆ
+ w3 nˆ
+ w3
( 3)
∧ nˆ
( 3)
∧ nˆ
) ⊗ nˆ
) ⊗ nˆ
( 2)
( 3)
( 2)
+
( 3)
w = −w2 (nˆ (3) ) ⊗ nˆ (1) + w3 (nˆ ( 2) ) ⊗ nˆ (1) +
( )
(nˆ ) ⊗ nˆ
( )
(nˆ ) ⊗ nˆ
+ w1 nˆ (3) ⊗ nˆ ( 2 ) − w3 nˆ (1) ⊗ nˆ ( 2 ) +
− w1
( 2)
( 3)
Además teniendo en cuanta que w1 = −w 23
w aún puede ser expresado por:
( 3)
+ w2 (1)
= w 32 , w2 = w13 = −w 31 , w3 = −w12 = w 21 ,
w = w 31 nˆ (3) ⊗ nˆ (1) + w 21 nˆ ( 2) ⊗ nˆ (1) +
+ w 32 nˆ (3) ⊗ nˆ ( 2 ) + w12 nˆ (1) ⊗ nˆ ( 2 ) +
+ w 23 nˆ ( 2 ) ⊗ nˆ (3) + w13 nˆ (1) ⊗ nˆ (3)
el cual es exactamente igual a
3
w = ∑ w ab nˆ (a ) ⊗ nˆ (b)
Los términos
w⋅V
a ,b =1
a ≠b
y V ⋅ w pueden ser obtenidos como sigue a continuación:

 3
  3


(a)
(b )
ˆ
ˆ
w ⋅ V =  w ab n ⊗ n  ⋅  λ b nˆ (b) ⊗ nˆ (b) 
  b =1
 a ,b =1


 a≠b
∑
=
3
∑
∑
λ b w ab nˆ ( a ) ⊗ nˆ (b ) ⋅ nˆ (b ) ⊗ nˆ (b ) =
a ,b =1
a ≠b
3
∑λ w
b
ab
nˆ ( a ) ⊗ nˆ (b )
a ,b =1
a≠b
y



 3
  3
(
)
(
)
(
)
(
)
a
a
a
b
V ⋅ w =  λ a nˆ ⊗ nˆ  ⋅ 
w ab nˆ ⊗ nˆ 

 a =1
  a ,b =1

 a≠b
∑
=
∑
3
∑λ w
a
ab
nˆ ( a ) ⊗ nˆ (b )
a ,b =1
a ≠b
Luego,
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
84
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS

  3
 3

 

(
)
(
)
(
)
(
)
a
b
a
b
w ⋅ V − V ⋅ w =  λ b w ab nˆ ⊗ nˆ  −  λ a w ab nˆ ⊗ nˆ 

  a ,b =1
 a ,b =1

  a≠b
 a ≠b
∑
=
3
∑w
∑
ab (λ b
− λ a ) nˆ ( a ) ⊗ nˆ (b )
a ,b =1
a ≠b
Análogamente, es posible demostrar que:
3
w ⋅ V 2 − V 2 ⋅ w = ∑ w ab (λ2b − λ2a ) nˆ ( a ) ⊗ nˆ (b)
a ,b =1
a ≠b
1.5.6
Teorema de Cayley-Hamilton
El teorema de Cayley-Hamilton afirma que cualquier tensor T satisface su propia ecuación
característica, es decir, si λ1 , λ 2 , λ 3 son los autovalores de T , podemos escribir:
λ 1
( T ) ij =  0
 0
0
λ2
0
0
0 
λ 3 
(1.318)
Y si estos autovalores satisfacen la ecuación: λ3 − λ2 I T + λ II T − III T = 0 , el tensor T
también la satisface, es decir:
T 3 − T 2 I T + T II T − III T 1 = 0
(1.319)
Una aplicación del teorema de Cayley-Hamilton es expresar la potencia de tensores T n
como una combinación de T n −1 , T n − 2 , T n −3 . Si queremos obtener T 4 queda:
T 3 ⋅ T − T 2 ⋅ TI T + T ⋅ T II T − III T 1 ⋅ T = 0
⇒ T 4 = T 3 I T − T 2 II T + III T T
(1.320)
Utilizando el teorema de Cayley-Hamilton podemos expresar el tercer invariante en función
de las trazas, que será útil a la hora de obtener las derivadas parciales de los invariantes.
Según el teorema de Cayley-Hamilton sigue siendo válida la expresión:
T 3 − I T T 2 + II T T − III T 1 = 0
(1.321)
Haciendo el doble producto escalar con el tensor identidad de segundo orden ( 1 ), la
expresión queda:
T 3 : 1 − I T T 2 : 1 + II T T : 1 − III T 1 : 1 = 0 : 1
(1.322)
Como ya hemos visto anteriormente, las siguientes relaciones son válidas T 3 : 1 = Tr ( T 3 ) ,
T 2 : 1 = Tr ( T 2 ) , T : 1 = Tr (T ) , 1 : 1 = Tr (1) = 3 , 0 : 1 = Tr (0) = 0 . Reemplazando en la
ecuación (1.322) obtenemos:
Tr ( T 3 ) − I T Tr ( T 2 ) + II T Tr ( T ) − III T Tr (1) = 0
123
[
=3
1
III T = Tr ( T 3 ) − I T Tr ( T 2 ) + II T Tr ( T )
3
]
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.323)
Por: Eduardo W.V. Chaves
1 TENSORES
85
Reemplazando los valores de los invariantes I T , II T , dados por la ecuación (1.278),
obtenemos:
1
3
1
3
III T =  Tr ( T 3 ) − Tr ( T 2 ) Tr ( T ) + [Tr ( T )] 
3
2
2

(1.324)
En notación indicial
1
3
1

III T =  Tij T jk Tki − Tij T ji Tkk + Tii T jj Tkk 
3
2
2

(1.325)
Ejemplo 1.37: Partiendo del teorema de Cayley-Hamilton obtener la inversa de un tensor
T en función de potencia de tensores.
Solución:
El teorema de Cayley-Hamilton afirma que:
T 3 − T 2 I T + T II T − III T 1 = 0
Haciendo el producto escalar de la expresión anterior por el tensor T −1 obtenemos que:
T 3 ⋅ T −1 − T 2 ⋅ T −1 I T + T ⋅ T −1 II T − III T 1 ⋅ T −1 = 0 ⋅ T −1
T 2 − TI T + 1 II T − III T T −1 = 0
⇒ T −1 =
(
1
T 2 − TI T + 1 II T
III T
)
El teorema de Cayley-Hamilton también es válido para matrices cuadradas de orden n . Sea
una matriz cuadrada An×n el determinante característico viene dado por:
λ1n×n − A = 0
(1.326)
donde 1n×n es la matriz identidad. Desarrollando el determinante obtenemos:
λn − I 1 λn −1 + I 2 λn − 2 − L (−1) n I n = 0
(1.327)
donde I 1 , I 2 , L , I n son los invariantes de la matriz A . Para el caso particular n = 3 y si A
representa las componentes del tensor A tenemos que: I 1 = I A , I 2 = II A , I 3 = III A .
Aplicando el teorema de Cayley-Hamilton se cumple que
A n − I 1A n −1 + I 2 A n − 2 − L + (−1) n I n 1 = 0
(1.328)
A través de la relación (1.328) podemos obtener la inversa de la matriz An×n , por ello
multiplicando todos los términos por A −1 , resultando:
A n A −1 − I 1A n −1A −1 + I 2 A n − 2 A −1 − L + (−1) n I n 1A −1 = 0
luego
⇒ A n −1 − I 1 A n − 2 + I 2 A n −3 − L (−1) n −1 I n −11 + (−1) n I n A −1 = 0
A −1 =
(
(−1) n −1
A n −1 − I 1A n − 2 + I 2 A n−3 − L (−1) n −1 I n −11
In
)
(1.329)
(1.330)
El invariante I n = det (A ) luego, sólo habrá la inversa de A si I n = det (A ) ≠ 0 .
Ejemplo 1.38: Dado el tensor T representado por sus componentes en el sistema
cartesiano:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
86
5 0 0 
T = 0 2 0
0 0 1 
Comprobar el teorema de Cayley-Hamilton.
Solución:
El teorema de Cayley-Hamilton también se aplica para las componentes del tensor:
T 3 − T 2 I T + T II T − III T 1 = 0
donde I T = 5 + 2 + 1 = 8 , II T = 10 + 2 + 5 = 17 , III T = 10 , luego:
T
3
5 3

=0
0

0
23
0
0  125 0 0 

0  =  0 8 0 
1   0 0 1 
; T
2
5 2

=0
0

0
22
0
0  25 0 0 

0  =  0 4 0 
1   0 0 1 
Aplicando el teorema de Cayley-Hamilton verificamos que:
1.5.7
125 0 0
 25 0 0
5 0 0 
1 0 0 
 0 8 0 − 8  0 4 0 + 17 0 2 0  − 10 0 1 0








 0 0 1 
 0 0 1 
0 0 1 
0 0 1 
1444444444442444444444443
0 0 0 
= 0 0 0 
0 0 0 
0 0 0 
0 0 0 


0 0 0
0 0 0 
= 0 0 0 
0 0 0 
c.q.d.
Módulo de un Tensor
El módulo de un tensor, también conocido como Norma de Frobenius, viene dado a
continuación:
r
r r
v = v ⋅ v = v i vi
(1.331)
T = T : T = Tij Tij
(1.332)
(tensor de tercer orden)
A = A : ⋅A = A ijk A ijk
(1.333)
(tensor de cuarto orden)
C = C :: C = C ijkl C ijkl
(1.334)
(vector)
(tensor de segundo orden)
r
Por ejemplo, la norma de un vector v , denominada norma Euclidiana, mide la magnitud
del vector. Para visualizar la norma de un tensor de segundo orden, consideremos que T
sea un tensor simétrico ( T = T T ) y que T1 , T2 , T3 sean sus autovalores, luego la norma,
que es un invariante, viene dada por:
T = T : T = Tr ( T T ⋅ T ) = Tr ( T 2 )
= Tij Tij = T12 + T22 + T32 = I T2 − 2 II T
(1.335)
En el espacio principal de T se puede visualizar la interpretación de la norma de T , ver
Figura 1.29. Como podemos ver es una medida de distancia.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
87
x 2′
T2
T
T1
x1′
T3
x3′
Figura 1.29: Norma de un tensor de segundo orden en el espacio principal.
1.5.8
Tensor Isótropo y Anisótropo
Un tensor se denomina isótropo cuando sus componentes son las mismas en cualquier
sistema de coordenadas, en caso contrario el tensor será anisótropo.
Consideremos las componentes de un tensor T representadas en forma matricial por T
en un sistema de referencia y las componentes del mismo tensor en cualquier otro sistema
obtenido por la transformación de base que representamos genéricamente por T ′ . Este
tensor se dice isótropo cuando cumple que:
Tensor Isótropo de orden uno
T =T ′
(1.336)
r
Consideremos un vector v representado por sus componentes v 1 , v 2 , v 3 en el sistema de
coordenadas x1 , x 2 , x3 . La representación de estas componentes en un nuevo sistema de
coordenadas x1′ , x 2′ , x3′ será v 1′ , v ′2 , v ′3 , por lo que es válido decir:
r
v = v i eˆ i = v ′j eˆ ′j
⇒
v ′i = a ij v j
(1.337)
r
Para que v sea isótropo por definición tiene que cumplir v i = v ′i y eso sólo será posible si
a ij = δ ij , i.e. eˆ i = eˆ ′j (no hubo cambio de sistema), ó v i = v ′i = 0 i . Luego, el único tensor
r
de orden uno isótropo es el vector nulo 0 .
Tensor Isótropo de segundo orden
Un ejemplo de un tensor isótropo de segundo orden es el tensor identidad 1 , representado
por sus componentes por δ kl . Utilizando la transformación de coordenadas para las
componentes de un tensor de segundo orden obtenido en (1.254), se demuestra que:
δ ′ij = a ik a jl δ kl = a ik a jk = δ ij
123
AA T =1
(1.338)
Una consecuencia inmediata del anterior es que cualquier tensor esférico ( α1 ) es un tensor
isótropo. Es decir, si un tensor de segundo orden es isótropo este tensor es esférico.
Tensor Isótropo de tercer orden
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
88
Un ejemplo de un tensor (pseudo) isótropo de orden tres es el pseudo-tensor Levi-Civita,
definido en (1.184) cuyas componentes son  lmn . Aplicando la ley de transformación de
coordenadas (1.256), resulta:
′ijk = a il a jm a kn  lmn = A  ijk =  ijk
{
(Ver Ejemplo 1.22)
(1.339)
1
Tensor Isótropo de cuarto orden
Si δ kl es isótropo, resulta sencillo demostrar que los siguientes tensores de cuarto orden
son también isótropos:
I ijkl = δ ij δ kl
I ijkl = δ ik δ jl
;
I ijkl = δ il δ jk
;
(1.340)
Se puede demostrar que cualquier tensor isótropo de cuarto orden puede ser representado
como una combinación lineal de los tres tensores dados anteriormente en (1.340):
D = a 0 I + a1 I + a 2 I
D = a 0 1 ⊗ 1 + a1 1⊗1 + a 2 1⊗1
(1.341)
D ijkl = a 0 δ ij δ kl + a1δ ik δ jl + a 2 δ il δ jk
Ejemplo 1.39: Demostrar que el tensor de cuarto orden que presenta simetría menor y
mayor C es isótropo, donde las componentes de este tensor vienen dadas por:
C ijkl = λ δ ij δ kl + µ (δ ik δ jl + δ il δ jk )
donde λ , µ son constantes.
Solución:
La ley de transformación de las componentes de un tensor de cuarto orden viene dada por:
C ′ijkl = a im a jn a kp a lq C mnpq
Considerando que C mnpq = λδ mn δ pq + µ (δ mp δ nq + δ mq δ np ) y reemplazando en la expresión
anterior, obtenemos que:
C ′ijkl = a im a jn a kp a lq [λδ mn δ pq + µ (δ mp δ nq + δ mq δ np )]
(
= λa im a jn a kp a lq δ mn δ pq + µ a im a jn a kp a lq δ mp δ nq + a im a jn a kp a lq δ mq δ np
(
= λa in a jn a kq a lq + µ a ip a jq a kp a lq + a iq a jn a kn a lq
(
= λδ ij δ kl + µ δ ik δ jl + δ il δ jk
)
)
)
= C ijkl
Con lo que demostramos que el tensor C es isótropo.
1.5.9
Tensores Coaxiales
Decimos que dos tensores de segundo orden simétricos T y S son coaxiales, si presentan
los mismos autovectores, luego:
T=
3
∑
a =1
Ta nˆ ( a ) ⊗ nˆ ( a )
;
S=
3
∑S
a
nˆ ( a ) ⊗ nˆ ( a )
(1.342)
a =1
donde Ta son los autovalores de T y S a son los autovalores de S . Es de fácil
demostración que, para que dos tensores sean coaxiales, es suficiente que el producto
escalar entre ellos sea conmutativo, es decir:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
T ⋅S = S ⋅ T
si
⇒
89
S , T son coaxiales
(1.343)
También podemos concluir que un tensor simétrico S , y su inversa S −1 son tensores
coaxiales puesto que S ⋅ S −1 = S −1 ⋅ S = 1 , y además recurriendo a sus representaciones
espectrales:
S=
3
∑
S a nˆ ( a ) ⊗ nˆ ( a )
S −1 =
;
a =1
siendo S a y
3
1 ˆ (a ) ˆ (a )
n ⊗n
∑S
a =1
(1.344)
a
1
, los autovalores de S y S −1 respectivamente.
Sa
Si S y T son tensores simétricos y coaxiales podemos demostrar que el tensor resultante
de la operación ( S ⋅ T ) resulta ser otro tensor simétrico. Para su demostración partimos de
la definición de tensores coaxiales:
T ⋅S = S ⋅ T
⇒
T ⋅S − S ⋅ T = 0
⇒
T ⋅ S − ( T ⋅ S ) T = 0 ⇒ 2( T ⋅ S ) anti = 0 (1.345)
Luego, si la parte antisimétrica de un tensor es cero resulta que este tensor es simétrico:
( T ⋅ S ) anti = 0
( T ⋅ S ) ≡ ( T ⋅ S ) sym
⇒
(1.346)
1.5.10 Descomposición Polar
Consideremos un tensor de segundo orden arbitrario, F , no singular ( det ( F ) ≠ 0 ⇒ ∃F −1 ).
Además, la proyección de F según dirección N̂ resulta un vector que lo representamos
r
ˆ = λ nˆ ≠ 0 , ya que det ( F ) ≠ 0 . Con eso, dada una
por su módulo y dirección como F ⋅ N
ˆ
(n)
ˆ ( a ) , podemos decir que:
base ortonormal N
F −1 ⋅ F = 1 =
3
∑ Nˆ
(a)
ˆ (a)
⊗N
a =1
⇒ F = F ⋅1 = F ⋅
3
∑ Nˆ
(a)
a =1
⇒F =
3
∑ λ nˆ
a
(a)
ˆ (a ) =
⊗N
3
∑ F ⋅ Nˆ
(a)
ˆ (a)
⊗N
(1.347)
a =1
ˆ (a )
⊗N
a =1
NOTA: Observemos que la representación de F , dada por (1.347), no es la
representación espectral de F en el sentido estricto de la palabra, ya que λ a no son los
ˆ ( a ) son los autovectores de F . ■
autovalores de F y tan poco nˆ ( a ) o N
ˆ ( a ) , la nueva base nˆ ( a ) no
Notar que para una base ortonormal arbitraria de N
ˆ ( a ) tal que la
necesariamente será una base ortogonal. Queremos encontrar una base N
r
ˆ (1 ) )
nueva base nˆ ( a ) sea una base ortonormal, ver Figura 1.30, i.e. f (N
r
⋅ f (N
ˆ (2) )
= 0,
r (Nˆ ( 2 ) ) r (Nˆ ( 23 )
r (Nˆ ( 3) ) r (Nˆ (1) )
f
⋅f
= 0, f
⋅f
= 0 . Luego, buscamos un espacio tal que se cumpla la
siguiente transformación ortogonal nˆ ( a ) = R ⋅ Nˆ ( a ) , el cual nos garantiza la ortogonalidad de
nˆ ( a ) , ya que una transformación ortogonal no cambian los ángulos entre vectores ni sus
magnitudes.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
90
r
r
ˆ (1) = f (Nˆ (1) ) = f (Nˆ (1) ) nˆ (1) = λ nˆ (1)
F ⋅N
1
r ˆ (1 )
ˆ (1)
f (N ) = F ⋅ N
r ˆ (2)
ˆ ( 2)
f (N ) = F ⋅ N
n̂
r
r
ˆ ( 2) = f (Nˆ ( 2 ) ) = f (Nˆ ( 2 ) ) nˆ ( 2 ) = λ nˆ ( 2 )
F ⋅N
2
r
r
ˆ (3) = f (Nˆ ( 3) ) = f (Nˆ ( 3) ) nˆ (3) = λ nˆ (3)
F ⋅N
3
N̂(3)
(1)
n̂( 2 )
N̂( 2 )
n̂(3)
N̂(1)
r ˆ (3)
ˆ ( 3)
f (N ) = F ⋅ N
ˆ (a) .
Figura 1.30: Proyección de F según la base N
ˆ ( a ) y nˆ ( a ) viene dada por la siguiente
Consideremos ahora que la transformación entre N
transformación ortogonal nˆ ( a ) = R ⋅ Nˆ ( a ) , podemos decir que:
F=
3
∑
ˆ (a) =
λ a nˆ ( a ) ⊗ N
a =1
3
∑
ˆ (a) ⊗ N
ˆ (a) = R ⋅
λ aR ⋅ N
a =1
3
∑ λ Nˆ
a
(a)
ˆ (a) = R ⋅ U
⊗N
(1.348)
a =1
3
ˆ (a) ⊗ N
ˆ ( a ) resulta un tensor
ˆ (a ) ⊗ N
ˆ ( a ) . Ya que N
donde hemos definido el tensor U = ∑ λ a N
a =1
simétrico, el tensor U también lo es, U = UT . Análogamente, pero ahora teniendo en
ˆ (a) ⇒ N
ˆ ( a ) = R T ⋅ nˆ ( a ) = nˆ ( a ) ⋅ R , podemos decir que:
cuenta que nˆ ( a ) = R ⋅ N
F=
3
∑ λ nˆ
a
a =1
(a)
ˆ (a ) =
⊗N
3
∑ λ nˆ
a
(a)
⊗ nˆ ( a ) ⋅ R =
a =1
3
∑λ
ˆ ( a ) ⊗ nˆ ( a ) ⋅ R = V ⋅ R
an
(1.349)
a =1
3
donde hemos definido el tensor V = ∑ λ a nˆ ( a ) ⊗ nˆ ( a ) . Verificamos que V es simétrico, y
a =1
comparando las representaciones espectrales de los tensores U y V , verificamos que
tienen los mismos autovalores y distintos autovectores. Luego, definimos la
descomposición polar como:
F = R ⋅U = V ⋅R
Descomposición polar
(1.350)
Recordemos del Ejemplo 1.27 que los tensores resultantes de las operaciones C = F T ⋅ F
y b = F ⋅ F T son tensores simétricos, y definidos positivos cuando det ( F ) ≠ 0 . Haciendo el
producto escalar por la izquierda por F T en la relación F = R ⋅ U obtenemos que:
T
F
F = F T ⋅ R ⋅ U = (R T ⋅ F ) T ⋅ U = UT ⋅ U = U 2 ⇒ U = ± F T ⋅ F = ± C
12⋅3
C
(1.351)
Análogamente podemos obtener que:
V = ± F ⋅FT = ± b
(1.352)
Puesto que los tensores C y b son tensores definidos positivos eso implica que los
autovalores de C y b son todos reales y positivos. Ahora bien, hasta ahora la única
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
91
restricción para el tensor F es que det ( F ) ≠ 0 , luego podemos tener las siguientes
posibilidades:
ƒ
Si det ( F ) > 0
En esta situación tenemos que det ( F ) = det (R )det(U) = det ( V )det(R ) > 0 , resultando las
siguientes posibilidades:
R − Tensor ortogonal propio
R − Tensor ortogonal impropio
ó

U, V − Tensores definidos positivos U, V − Tensores definidos negativos
ƒ
Si det ( F ) < 0
En esta situación tenemos que det ( F ) = det (R )det (U) = det ( V )det (R ) < 0 , resultando las
siguientes posibilidades:
R − Tensor ortogonal propio
R − Tensor ortogonal impropio
ó

U, V − Tensores definidos negativos U, V − Tensores definidos positivos
NOTA: En el capítulo 2 trabajaremos con unos tensores particulares donde F es no
singular ( det ( F ) ≠ 0 ) y det ( F ) > 0 . Los tensores U y V son tensores definidos positivos,
y el tensor R es un tensor de rotación, es decir, tensor ortogonal propio. ■
1.5.11 Derivada Parcial con Tensores
La primera derivada de un tensor con respecto a él mismo viene definido como:
∂A
= A ,A
∂A
=
∂A ij
∂A kl
(eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l )
(1.353)
= δ ik δ jl (eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l )
= I (tensor identidad de cuarto orden)
Podemos entonces obtener la derivada de la traza de un tensor respecto a él mismo:
∂A kk
∂[Tr ( A )]
≡ [Tr ( A )],A =
(eˆ i ⊗ eˆ j ) = δ ki δ kj (eˆ i ⊗ eˆ j ) = δ ij (eˆ i ⊗ eˆ j ) = 1
∂A
∂A ij
(1.354)
La derivada parcial de la traza al cuadrado de un tensor respecto al él mismo:
∂[Tr ( A )]
∂[Tr ( A )]
= 2 Tr ( A )1
= 2 Tr ( A )
∂A
∂A
2
(1.355)
La derivada parcial de la traza del cuadrado un tensor respecto al él mismo:
[
∂ Tr ( A 2 )
∂A
]
=

∂ ( A sr A rs )
∂ ( A sr )
∂( A rs ) 
+ A sr
(eˆ i ⊗ eˆ j ) =  A rs
 (eˆ i ⊗ eˆ j )
∂A ij
∂A ij
∂A ij 

[
]
[
]
= A rs δ si δ rj + A sr δ ri δ sj (eˆ i ⊗ eˆ j ) = A ji + A ji (eˆ i ⊗ eˆ j )
(1.356)
= 2 A ji (eˆ i ⊗ eˆ j ) = 2A T
Queda al lector la demostración de:
[
∂ Tr ( A 3 )
∂A
]
= 3( A 2 ) T
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
(1.357)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
92
Luego, si consideramos un tensor de segundo orden simétrico C , podemos decir que:
∂[Tr (C)]
=1;
∂C
[
3
∂ Tr (C )
∂C
]
[
∂[Tr (C)]
= 2 Tr (C)1 ;
∂C
2
∂ Tr (C 2 )
∂C
]
= 2C T = 2C ;
(1.358)
= 3(C 2 ) T = 3C 2
y además podemos decir que la derivada de la norma del tensor simétrico C viene dada
por:
∂ Tr (C ⋅ C T ) 
∂ Tr (C 2 ) 
∂ C:C


 = 1 Tr (C 2 )
=
=
= 
∂C
∂C
∂C
∂C
2
−1
1
= Tr (C 2 ) 2 2C
2
∂C
(
)
[
[
] [Tr(C )],
−1
2
]
2
C
(1.359)
o aún:
∂C
∂C
C
C
=
(1.360)
Otra aplicación interesante viene a continuación:
(
∂ n i C ij n j
)
∂n k
=
∂n j
∂n i
C ij n j + n i C ij
= δ ik C ij n j + n i C ij δ jk
∂n k
∂n k
(1.361)
= C kj n j + n i C ik = C kj n j + C jk n j
= 2C kj n j
donde hemos considerado que C es simétrico, i.e., C kj = C jk .
Consideremos aún el tensor de segundo orden simétrico C . Para obtener la derivada
parcial de su inversa con respecto a él mismo partimos de la siguiente condición:
(
)
∂1 ∂ C −1 ⋅ C
=O
=
∂C
∂C
(1.362)
donde O es el tensor nulo de cuarto orden. La expresión anterior en notación indicial
queda:
(
∂ C iq−1C qj
∂C kl
( )C
) = ∂(C ) C
−1
iq
∂C kl
∂ C iq−1
∂C kl
⇒
qj
=
( )δ
∂ C iq−1
∂C kl
qr
−C iq−1
( )
∂ C qj
∂C kl
= −C iq−1
Considerando que C qj =
+ C iq−1
qj
(
( )
∂ C qj
∂C kl
( )
∂ C qj
∂C kl
⇒
= O ikjl
( )C
∂ C iq−1
∂C kl
−1
qj C jr
= −C iq−1
( )
∂ C qj
∂C kl
C −jr1
(1.363)
C −jr1
)
1
C qj + C jq , la expresión anterior queda:
2
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
( )δ
∂ C iq−1
∂C kl
qr
= −C iq−1
( )
(
93
)
1  ∂ C qj + C jq  −1

 C jr
∂C kl
2

[
∂ C ir−1
1
1
= −C iq−1 δ qk δ jl + δ jk δ ql C −jr1 = − C iq−1δ qk δ jl C −jr1 + C iq−1δ jk δ ql C −jr1
2
2
∂C kl
( )
[
]
[
∂ C ir−1
1
= − C ik−1C lr−1 + C il−1 C −kr1
2
∂C kl
]
(1.364)
]
En notación tensorial queda:
[
1
∂C −1
= − C −1 ⊗C −1 + C −1 ⊗C −1
2
∂C
]
(1.365)
NOTA: Observemos que si no hubiéramos reemplazando la parte simétrica de C qj en
( )δ
∂ C iq−1
(1.363), hubiéramos obtenido que
∂C kl
qr
= −C iq−1
( )
∂ C qj
∂C kl
C −jr1 = −C iq−1δ qk δ jl C −jr1 = −C ik−1C lr−1 .
Resultando un tensor no simétrico. ■
1.5.11.1 Derivada Parcial de los Invariantes
Las derivadas parciales de los invariantes principales de un tensor de segundo orden se
obtienen a continuación:
Derivada parcial de I T con respecto a T , ver ecuación (1.354):
∂[I T ] ∂[Tr ( T )]
= [Tr ( T )], T = 1
=
∂T
∂T
(1.366)
Derivada parcial de II T con respecto a T :
[
2
∂[ II T ] ∂  1
∂ Tr ( T 2 )
1  ∂[Tr ( T )]
2
2 
−
=
 [Tr ( T )] − Tr ( T )  = 
∂T
∂T
∂T
∂T  2
2 

1
= 2( TrT )1 − 2 T T
2
= Tr ( T )1 − T T
[
]
[
]
]

(1.367)
Aún podemos expresar (1.367) remplazando T T , obtenido por el teorema de CayleyHamilton:
T 3 : T −2 − I T T 2 : T −2 + II T T : T −2 − III T 1 : T −2 = 0
T − I T 1 + II T T −1 − III T T − 2 = 0
(1.368)
⇒ T = I T 1 − II T T −1 + III T T − 2
Luego,
∂[ II T ]
= Tr ( T )1 − T T = Tr ( T )1 − I T 1 − II T T −1 + III T T − 2
∂T
(
(
= II T T
−1
− III T T
)
−2 T
)
T
(1.369)
Para obtener la derivada del tercer invariante, utilizaremos la definición dada por (1.324):
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
94
∂[ III T ]
3
∂ 1
1
1
3
2
=
 Tr ( T ) − Tr ( T ) Tr ( T ) + [Tr ( T )] 
∂T
∂T  3
2
6

[
]
2
1
1 ∂ Tr ( T 2 )
1
∂[Tr ( T )] 3
= 3( T 2 ) T −
+ [Tr ( T )] 1
Tr ( T ) − Tr ( T 2 )
3
2
∂T
2
∂T
6
= ( T 2 ) T − Tr ( T ) T T −
2
1
1
Tr ( T 2 )1 + [Tr ( T )] 1
2
2
= ( T 2 ) T − Tr ( T ) T T +
2
1
[Tr(T )] − Tr( T 2 ) 1
2
[
(1.370)
]
= ( T 2 ) T − I T T T + II T 1
Si multiplicamos por la inversa del tensor T en la ecuación (1.321) obtenemos:
T 3 ⋅ T −1 − I T T 2 ⋅ T −1 + II T T ⋅ T −1 − III T 1 ⋅ T −1 = 0
T 2 − I T T + II T 1 − III T T −1 = 0
(1.371)
⇒ III T T −1 = T 2 − I T T + II T 1
y la transpuesta:
( III
TT
) = (T
−1 T
2
− I T T + II T 1
) = (T )
T
2 T
− I T T T + II T 1
(1.372)
Reemplazando ecuación (1.372) en la expresión (1.370) obtenemos:
(
∂[ III T ]
= III T T −1
∂T
)
T
= III T T −T
(1.373)
1.5.11.2 Derivada Temporal de Tensores
Asumamos que un tensor de segundo orden depende de un parámetro t , que es el tiempo.
Definimos la primera derivada temporal y la segunda derivada temporal del tensor T ,
respectivamente, por:
D
T ≡ T&
Dt
D2
&&
T≡T
2
Dt
;
(1.374)
La derivada temporal del determinante de un tensor viene definida como:
DT
D
[det(T )] = ij cof Tij
Dt
Dt
( )
(1.375)
donde cof (Tij ) es el cofactor de Tij y definido como [cof (Tij )]T = det(T ) (T −1 )ij .
1
1
Ejemplo 1.40: Considérese J = [det (b )] 2 = ( III b ) 2 , donde b es un tensor de segundo
orden simétrico, b = b T . Obtener la derivada de J y de ln(J ) con respecto a b .
Solución:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
⇒
⇒
95
1


∂ ( III b ) 2 
∂J

= 
∂b
∂b
1 ∂ III
1
1
1
b
= ( III b )− 2
= ( III b )− 2 III b b −T
2
2
∂b
1
1
1
= ( III b ) 2 b −1 = J b −1
2
2
1
 

∂ ln III b 2 
∂[ln( J )]
1 ∂ III b 1 −1


= 
= b
=
∂b
2 III b ∂b
2
∂b
1.5.12 Tensor Esférico y Desviador
Cualquier tensor puede ser descompuesto en una parte esférica y en otra parte desviadora.
Luego, para un tensor T esta descomposición viene dada por:
T = T esf + T dev =
= Tm 1 + T
I
Tr ( T )
1 + T dev = T 1 + T dev
3
3
(1.376)
dev
El tensor desviador de T vendrá definido como:
T dev = T −
Tr ( T )
1 = T − Tm 1
3
(1.377)
Para las operaciones siguientes consideraremos que T es un tensor simétrico ( T = T T )
luego, en estas condiciones las componentes del tensor T dev vienen dadas por:
Tijdev
 T11dev

=  T12dev
 T dev
 13
T12dev
dev
T22
dev
T23
T13dev   T11 − Tm

dev 
T23
 =  T12
T33dev   T13
 13 ( 2 T11 − T22 − T33 )

T12
=

T13

T12
T22 − Tm
T23
T12
1
3
(2 T22 − T11 − T33 )
T23



T33 − Tm 
T13
T23


T23

1
(2 T33 − T11 − T22 )
3
T13
(1.378)
Podemos también hacer la representación de las componentes del tensor dado por (1.376)
en la base cartesiana tal y como se indica en la Figura 1.31.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
96
x3
T 33
T23
T13
T13
T23
T12
T22
T12
x2
T11
x
14414444442444444443
x3
x3
Tm
T33dev
T23
T13
Tm
T13
+
Tm
x2
T23
T12
dev
T22
T12
T11dev
x1
x2
x1
Figura 1.31: Parte esférica y desviadora de un tensor de segundo orden.
1.5.12.1 Primer Invariante del Tensor Desviador
Los invariantes del tensor desviador ( T dev ) pueden ser obtenidos en función de los
invariantes principales de T :
I
T dev
Tr ( T ) 
Tr ( T )

= Tr ( T dev ) = Tr  T −
1 = Tr ( T ) −
Tr (1) = 0
3
3 123


δ =3
(1.379)
ii
Con lo que concluimos que la traza de cualquier tensor desviador es cero.
1.5.12.2 Segundo Invariante del Tensor Desviador
Para obtener el segundo y tercer invariante del tensor desviador utilizaremos el espacio de
las direcciones principales por simplicidad. En este espacio se cumple que:
Componentes del tensor:
 T1
Tij =  0
 0
0
T2
0
0
0 
T3 
(1.380)
Invariantes principales: I T = T1 + T2 + T3 , II T = T1 T2 + T2 T3 + T3 T1 , III T = T1 T2 T3 .
Las componentes del tensor desviador definido en (1.377) ( T dev = T − Tm 1 ) en el espacio
de las direcciones principales son:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
 T1 − Tm
=  0
 0
Tijdev
0
T2 − Tm
0
97



T3 − Tm 
0
0
(1.381)
El segundo invariante del tensor desviador de T puede ser obtenido como:
= ( T1 − Tm )( T2 − Tm ) + ( T1 − Tm )( T3 − Tm ) + ( T2 − Tm )( T3 − Tm )
II T dev
= ( T1 T2 + T1 T3 + T2 T3 ) − 2 Tm ( T1 + T2 + T3 ) + 3 Tm2
2I
I2
= II T − T ( I T ) + T
3
3
1
2
= 3 II T − I T
3
(
(1.382)
)
También podríamos haber obtenido el resultado anterior partiendo directamente de la
definición del segundo invariante de un tensor dado en (1.278):
II
T dev
{
]}
[
{ [
]}
1
1
( I dev ) 2 − Tr ( T dev ) 2 = − Tr ( T dev ) 2
T
2
2
1
1
= − Tr ( T − Tm 1) 2 = {− Tr[( T − Tm 1) ⋅ ( T − Tm 1)]}
2
2
1
1
= − Tr ( T 2 − 2 Tm T ⋅ 1 + Tm2 1) = − Tr ( T 2 ) + 2 Tm Tr ( T ) − Tm2 Tr (1)
2
2
2
I
I 
1
=  − Tr ( T 2 ) + 2 T I T − T 3
2
3
9 
=
{ [
]}
{ [
=
]} [
]
(1.383)
I T2 
1
2
(
)
Tr
T
−
+


2
3
Teniendo en cuenta que Tr ( T 2 ) = T12 + T22 + T32 = I T2 − 2 II T , ver Ejemplo 1.33, la relación
anterior (1.383) resulta:
II T dev =
I T2  1 
2 I T2  1
1 2
2
 − I T + 2 II T +
 = 2 II T −
 = 3 II T − I T
2
3  2
3  3
(
)
(1.384)
Otra expresión que podemos encontrar en la literatura, para el segundo invariante de un
tensor desviador, es en función de las componentes del tensor desviador. Utilizando la
expresión (1.383):
II
T dev
=−
[
]
[
]
1
1
1
Tr ( T dev ) 2 = − Tr ( T dev ⋅ T dev ) = − T dev
2
2
2
⋅ ⋅T dev = − 1 Tijdev T jidev
2
(1.385)
Expandiendo la expresión anterior obtenemos:
II
T dev
=−
[
1
dev 2
dev 2
( T11dev ) 2 + ( T22
) + ( T33dev ) 2 + 2( T12dev ) 2 + 2( T13dev ) 2 + 2( T23
)
2
]
(1.386)
En el espacio de las direcciones principales:
II
T dev
=−
[
1 dev dev
1
Tij T ji = − ( T1dev ) 2 + ( T2dev ) 2 + ( T3dev ) 2
2
2
]
(1.387)
Otra forma de expresar el segundo invariante viene demostrada a continuación:
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
98
II T dev =
dev
T22
dev
T23
dev
T23
T33dev
+
T11dev
T13dev
T13dev
T33dev
+
T11dev
T12dev
T12dev
dev
T22
[
]
1
dev dev
dev
dev 2
) − ( T13dev ) 2
= − − 2 T22
T33 − 2 T11dev T33dev − 2 T11dev T22
− ( T12dev ) 2 − ( T23
2
(1.388)
O aún:
( ) − 2 T T + (T ) + (T ) − 2 T T + (T )
) − 2 T T + (T )  + (T ) + (T ) + (T )
1
dev
II T dev = −  T22
2 
(T
dev 2
11
2
dev
22
dev
11
dev
22
dev 2
33
dev
33
dev 2
22
dev 2
11
dev 2
11
dev
11
dev 2
22
dev
33
dev 2
33
dev 2
33
+
(1.389)
dev 2
) − ( T13dev ) 2
− ( T12dev ) 2 − ( T23
Observa que de la ecuación (1.321) obtenemos que:
dev 2
( T11dev ) 2 + ( T22
) + ( T33dev ) 2 = −2 II
T dev
dev 2
− 2( T12dev ) 2 − 2( T13dev ) 2 − 2( T23
)
(1.390)
Reemplazando (1.390) en la expresión (1.389) obtenemos:
II
T dev
=−
[
]
1
dev
dev 2
dev 2
( T22
− T33dev ) 2 + ( T11dev − T33dev ) 2 + ( T11dev − T22
) − ( T12dev ) 2 − ( T23
) − ( T13dev ) 2
6
(1.391)
Y si consideramos las direcciones principales:
II
T dev
=−
[
1
( T2dev − T3dev ) 2 + ( T1dev − T3dev ) 2 + ( T1dev − T2dev ) 2
6
]
(1.392)
1.5.12.3 Tercer Invariante del Tensor Desviador
El tercer invariante del tensor desviador de T queda:
III T dev
= ( T1 − Tm )( T2 − Tm )( T3 − Tm )
= T1 T2 T3 − Tm ( T1 T2 + T1 T3 + T2 T3 ) + Tm2 ( T1 + T2 + T3 ) − Tm3
I
I2
I3
= III T − T II T + T I T − T
3
9
27
I T II T 2 I T3
= III T −
+
3
27
1
3
=
2 I T − 9 I T II T + 27 III T
27
(
(1.393)
)
Otra forma de expresar el tercer invariante es:
III
T dev
= T1dev T2dev T3dev =
1 dev dev dev
Tij T jk Tki
3
(1.394)
Ejemplo 1.41: Considérese un tensor de segundo orden simétrico σ y su parte desviadora
s ≡ σ dev . Obtener el resultado de la operación s :
∂s
. Demostrar también que los tensores
∂σ
σ y σ dev son tensores coaxiales.
Solución: Teniendo la definición de un tensor desviador σ = σ esf + σ dev = σ esf + s .
Obtenemos que: s = σ −
Iσ
1 . Luego:
3
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
En notación indicial:
I


∂ σ − σ 1 
3
∂s
 = ∂[σ ] − 1 ∂[I σ ] 1
= 
3 ∂σ
∂σ
∂σ
∂σ
∂s ij
∂σ kl
Con lo cual
s ij
∂s ij
∂σ kl
99
=
∂σ ij
∂σ kl
−
1 ∂ [I σ ]
1
δ ij = δ ik δ jl − δ kl δ ij
3 ∂σ kl
3
1
1
1


= s ij  δ ik δ jl − δ kl δ ij  = s ij δ ik δ jl − s ij δ kl δ ij = s kl − δ kl s ii = s kl
{
3
3
3


=0
s:
∂s
=s
∂σ
Para demostrar que dos tensores son coaxiales, hay que cumplir que σ dev ⋅ σ = σ ⋅ σ dev :
σ ⋅ σ dev = σ ⋅ (σ − σ esf ) = σ ⋅ σ − σ ⋅ σ esf = σ ⋅ σ − σ ⋅
Iσ
1
3
Iσ
I
1 = σ ⋅σ − σ 1⋅σ
3
3
Iσ 

= σ −
1  ⋅ σ = σ dev ⋅ σ
3


Con lo cual demostramos que los tensores σ y σ dev son coaxiales, es decir, tienen las
= σ ⋅σ − σ ⋅
mismas direcciones principales.
Mecánica del Medio Continuo: Conceptos Básicos (3ªEdición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
100
1.6 Función de Tensores
Una función de tensores puede resultar ser un escalar, un vector, o tensores de orden
superior. Como ejemplo de una función tensores de valor-escalar tenemos:
Ψ = Ψ ( T ) = det (T )
Ψ = Ψ (T , S) = T : S
(1.395)
donde T y S son tensores de segundo orden. Como ejemplo de función de tensores cuyo
argumento es un tensor de segundo orden (valor-tensor de segundo orden) tenemos:
Π = Π (T ) = α1 + βT + γ T 2
(1.396)
con α , β , γ escalares.
1.6.1
Series de Tensores
Dada una función f (x) podemos aproximar esta función a través de serie de Taylor por
∞
1 ∂ n f (a)
( x − a ) n , donde n! representa el factorial de n y f (a) el valor de la
n
!
n
∂x
n =0
función en el punto de aplicación x = a . Podemos extrapolar esta definición para tensores.
f ( x) =
∑
Por ejemplo, supongamos la función tensor tipo escalar ψ que es función del tensor de
segundo orden E , luego utilizando serie podemos aproximar la función ψ por:
ψ( E ) ≈
1
1 ∂ψ ( E 0 )
1 ∂ 2 ψ( E 0 )
( E ij − E 0 ij ) +
( E ij − E ij 0 )( E kl − E kl 0 ) + L
ψ( E 0 ) +
0!
1! ∂E ij
2! ∂E ij ∂E kl
∂ψ ( E 0 )
∂ 2 ψ( E 0 )
1
≈ ψ0 +
: (E − E0 ) + (E − E0 ) :
: (E − E0 ) + L
∂E
∂E ⊗ ∂E
2
(1.397)
Supongamos ahora que un tensor de segundo orden S sea una función de otro tensor de
segundo orden E , luego podemos aproximar S (E ) como:
∂ 2 S( E 0 )
1
1 ∂S ( E 0 )
1
S( E 0 ) +
: (E − E0 ) + (E − E0 ) :
: (E − E0 ) + L
0!
1! ∂E
2!
∂E ⊗ ∂E
∂S ( E 0 )
∂ 2S( E 0 )
1
≈ S0 +
: (E − E0 ) + (E − E0 ) :
: (E − E0 ) + L
∂E
2
∂E ⊗ ∂E
S( E ) ≈
(1.398)
Otras expresiones algebraicas de tensores pueden ser representadas mediante series como:
1 2 1 3
S + S +L
2!
3!
1
1
ln(1 + S ) = S − S 2 + S 3 − L
2
3
1
1
sin(S ) = S − S 3 + S 5 − L
3!
5!
exp S = 1 + S +
(1.399)
Consideremos un tensor S de segundo orden simétrico e isótropo, por lo que puede ser
representado por su forma espectral como:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
exp S =

3
∑ 1 + S
a =1 
a
+
101

S a2 S 3a
+
+ L nˆ ( a ) ⊗ nˆ ( a ) =
2!
3!

3
∑ exp
1
1


ln(1 + S ) =  S a − S 2a + S 3a + L nˆ ( a ) ⊗ nˆ ( a ) =
2
3

a =1 
∑
donde S a y nˆ
nˆ ( a ) ⊗ nˆ ( a )
a =1
3
(a )
Sa
(1.400)
3
∑ ln(1 + S
ˆ
a)n
(a )
⊗ nˆ
(a)
a =1
son los autovalores y autovectores, respectivamente, del tensor S .
Podemos extender estos conceptos para obtener la definición de una función de tensión
del tipo
1
m
S
, donde m es un número entero. Si definimos
 1  1   1
S =  S m  S m  L  S m
 


 


  1
 = S m 

 

 
1
m
S
como:
m
(1.401)
La forma espectral correspondiente viene dada por:
1
Sm
=
3
∑
1
m
Sa
(1.402)
nˆ ( a ) ⊗ nˆ ( a )
a =1
con lo que nos permite obtener
1.6.2
1
Sm
una vez conocidos
1
m
Sa
y nˆ ( a ) .
Función Isótropa de Tensores
Si Π = Π (T ) es una función tensor isótropa del tensor T , luego esta función es un
invariante bajo una transformación ortogonal:
(
)
Π * (T ) = Q ⋅ Π (T ) ⋅ Q T = Π Q ⋅ T ⋅ Q T
14
4244
3
( )
ΠT
(1.403)
*
Si T es un tensor simétrico podemos expresarlo según su representación espectral como:
T=
3
∑λ
ˆ ( a ) ⊗ nˆ ( a ) = λ 1nˆ (1) ⊗ nˆ (1) + λ 2 nˆ ( 2) ⊗ nˆ ( 2 ) + λ 3nˆ (3) ⊗ nˆ (3)
an
(1.404)
a =1
donde λ a son los autovalores de
correspondientes.
T
y nˆ ( a ) son las direcciones principales
Podemos demostrar que Π (T ) presenta las mismas direcciones principales de T , es decir,
Π ( T ) y T son tensores coaxiales.
Para esta demostración consideremos las componentes de T según las direcciones
principales:
(T )ij
λ 1
=  0
 0
0
λ2
0
0
0 
λ 3 
(1.405)
Los términos λ 1 , λ 2 , λ 3 son los valores principales de T . Luego, la función de tensor
vendrá dada en función de los valores principales de T : Π = Π (λ 1 , λ 2 , λ 3 ) . Si T es
isótropo se cumple que:
T * = Q ⋅ T ⋅ QT
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.406)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
102
Análogamente para la función Π :
Π * (T ) = Q ⋅ Π (T ) ⋅ Q T
(1.407)
Adoptemos como las componentes del tensor ortogonal las siguientes:
(Q)ij
0
1 0

= 0 − 1 0 
0 0 − 1
(1.408)
Efectuando la operación (1.407) obtenemos:
 Π 11 − Π 12 − Π 13   Π 11
Π = − Π 12 Π 22 − Π 23  = Π 12
 − Π 13 − Π 23 Π 33  Π 13
0
0 
Π 11

*
0 
⇒ Π =  0 Π 22
 0
0
Π 33 
*
Π 12
Π 22
Π 23
Π 13 
Π 23  = Π
Π 33 
(1.409)
Para que se cumpla que Π * = Π (isotropía) concluimos que: Π 12 = Π 13 = Π 23 = 0 . Luego,
Π (T ) y T presentan las mismas direcciones principales.
Consideremos una función Π , que es función del tensor T . Esta función de tensión será
isótropa si y sólo si podemos representarla a través de la siguiente transformación,
Truesdell & Noll (1965):
Π = Π(T ) = Φ 0 1 + Φ1T + Φ 2 T 2
(1.410)
donde Φ 0 , Φ 1 , Φ 2 son funciones de los invariantes del tensor o autovalores de T .
La demostración sigue a continuación. Consideremos la representación espectral de la
función de tensión Π :
Π=
3
∑ ω (λ , λ
a
1
2 , λ3
) nˆ (a ) ⊗ nˆ ( a ) = ω1nˆ (1) ⊗ nˆ (1) + ω 2 nˆ ( 2) ⊗ nˆ ( 2) + ω3nˆ (3) ⊗ nˆ (3)
(1.411)
a =1
Observemos que los autovalores de Π , ω a (λ 1 , λ 2 , λ 3 ) , están en función de los autovalores
de T y que ellos presentan las mismas direcciones principales nˆ (i ) . Representaremos
ω a (λ 1 , λ 2 , λ 3 ) simplemente por ω a por simplicidad.
Podemos montar el siguiente sistema:
1 = nˆ (1) ⊗ nˆ (1) + nˆ ( 2) ⊗ nˆ ( 2) + nˆ (3) ⊗ nˆ (3)

(1)
(1)
(2)
(2)
( 3)
( 3)
T = λ 1nˆ ⊗ nˆ + λ 2 nˆ ⊗ nˆ + λ 3nˆ ⊗ nˆ
 2
2 (1)
(1)
2 (2)
( 2)
2 ( 3)
( 3)
T = λ 1nˆ ⊗ nˆ + λ 3nˆ ⊗ nˆ + λ 3nˆ ⊗ nˆ
(1.412)
Resolviendo el sistema anterior obtenemos nˆ ( a ) ⊗ nˆ ( a ) ≡ M ( a ) en función del tensor T y
dados por:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
M (1) =
103
λ 2λ3
(λ 2 + λ 3 )
T2
1−
T+
(λ 1 − λ 3 )(λ 1 − λ 2 )
(λ 1 − λ 3 )(λ 1 − λ 2 )
(λ 1 − λ 3 )(λ 1 − λ 2 )
M ( 2) =
M ( 3) =
(λ 1 + λ 3 )
λ 1λ 3
T2
1−
T+
(λ 2 − λ 1 )(λ 2 − λ 3 )
(λ 2 − λ 1 )(λ 2 − λ 3 )
(λ 2 − λ 1 )(λ 2 − λ 3 )
(1.413)
(λ 1 + λ 2 )
λ 1λ 2
T2
1−
T+
(λ 3 − λ 1 )(λ 3 − λ 2 )
(λ 3 − λ 1 )(λ 3 − λ 2 )
(λ 3 − λ 1 )(λ 3 − λ 2 )
Obviamente si reemplazamos los valores de nˆ ( a ) ⊗ nˆ ( a ) ≡ M ( a ) en la expresión (1.404)
obtenemos que T = T . Reemplazando ahora los valores de nˆ ( a ) ⊗ nˆ ( a ) ≡ M ( a ) en la
expresión (1.411) obtenemos que:
Π = Π(T ) = Φ 0 1 + Φ1T + Φ 2 T 2
(1.414)
donde los coeficientes Φ 0 , Φ 1 , Φ 2 son funciones de los autovalores de T y dados por:
Φ0 =
ω1 λ 2 λ 3
ω 2 λ 1λ 3
ω 3 λ 1λ 2
+
+
(λ 1 − λ 3 )(λ 1 − λ 2 ) (λ 2 − λ 1 )(λ 2 − λ 3 ) (λ 3 − λ 1 )(λ 3 − λ 2 )
Φ1 = −
Φ2 =
ω1 (λ 2 + λ 3 )
ω 2 (λ 1 + λ 3 )
ω3 (λ 1 + λ 2 )
−
−
(λ 1 − λ 3 )(λ 1 − λ 2 ) (λ 2 − λ 1 )(λ 2 − λ 3 ) (λ 3 − λ 1 )(λ 3 − λ 2 )
(1.415)
ω3
ω1
ω2
+
+
(λ 1 − λ 3 )(λ 1 − λ 2 ) (λ 2 − λ 1 )(λ 2 − λ 3 ) (λ 3 − λ 1 )(λ 3 − λ 2 )
Podríamos haber demostrado que una función tensor isótropa cumpla (1.414) partiendo de
la siguiente expresión:
Π * (T ) = Q ⋅ Π (T ) ⋅ Q T
(
= Q ⋅ Φ 0 1 + Φ1T + Φ 2 T 2
)⋅ Q
T
= Φ 0 Q ⋅ 1 ⋅ Q T + Φ 1Q ⋅ T ⋅ Q T + Φ 2 Q ⋅ T 2 ⋅ Q T
= Φ 0 1 + Φ1 T * + Φ 2 T
(1.416)
*2
= Π(T * )
1.6.3
Derivada Parcial de Función de Tensores
Consideremos una función escalar que es función de un tensor A :
Π = Π (A )
(1.417)
La derivada parcial de Π con respecto a A viene definida como:
∂Π
∂Π ˆ
= Π,A =
(ei ⊗ eˆ j )
∂A
∂A ij
(1.418)
donde la coma se utiliza para indicar derivada parcial.
La segunda derivada resultará un tensor de cuarto orden:
∂ 2Π
∂ 2Π
= Π , AA =
(eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l ) = D ijkl (eˆ i ⊗ eˆ j ⊗ eˆ k ⊗ eˆ l )
∂A ⊗ ∂A
∂A ij ∂A kl
(1.419)
Consideremos dos tensores de segundo orden simétricos definidos positivos C y b , donde
estos tensores vienen dados por las relaciones:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
104
C = FT ⋅F
;
b = F ⋅FT
(1.420)
donde F es un tensor de segundo orden arbitrario con det ( F ) > 0 .
Sea Ψ = Ψ (I C , II C , III C ) una función escalar de los invariantes principales del tensor C ,
donde se cumple que I C = I b , II C = II b , III C = III b . Obtendremos la derivada de Ψ con
respecto a C y con respecto a b y comprobaremos que la siguiente igualdad es válida:
F ⋅ Ψ , C ⋅F T = Ψ , b ⋅b
(1.421)
Utilizando la regla de la cadena podemos obtener que:
Ψ ,C =
∂Ψ (I C , II C , III C ) ∂Ψ ∂I C
∂Ψ ∂ II C
∂Ψ ∂ III C
=
+
+
∂C
∂I C ∂C ∂ II C ∂C
∂ III C ∂C
(1.422)
Considerando las derivadas parciales de los invariantes, vistas anteriormente, podemos
decir que:
∂I C
=1
∂C
∂ II C
= I C 1 − C T = I C 1 − C = II C C −1 − III C C − 2
∂C
∂ III C
= III C C −T = III C C −1 = C 2 − I C C + II C 1
∂C
Luego, considerando
resulta:
(1.423)
∂ II C
∂ III C
∂I C
=1,
= IC 1 − C y
= III C C −1 , la expresión (1.422)
∂C
∂C
∂C
Ψ ,C =
∂Ψ
∂Ψ
(I C 1 − C ) + ∂Ψ III C C −1
1+
∂I C
∂ II C
∂ III C
 ∂Ψ

 ∂Ψ
∂Ψ
Ψ , C = 
+
I C 1 − 
 ∂I C ∂ II C

 ∂ II C
(1.424)

 ∂Ψ

C + 
III C C −1

 ∂ III C

Otra forma de expresar la relación (1.425) es considerando
∂ III C
= C 2 − I C C + II C 1 , obteniendo así:
∂C
∂ II C
∂I C
=1,
= IC 1 − C y
∂C
∂C
 ∂Ψ

 ∂Ψ

 ∂Ψ
∂Ψ
∂Ψ
∂Ψ
Ψ , C = 
+
IC +
II C 1 − 
+
I C C + 
∂ III C
 ∂I C ∂ II C

 ∂ II C ∂ III C

 ∂ III C
Considerando ahora
además:
 ∂Ψ
Ψ , C = 
 ∂I C
(1.425)
 2
C

(1.426)
∂ II C
∂ III C
∂I C
=1,
= II C C −1 − III C C − 2 y
= III C C −1 obtenemos
∂C
∂C
∂C

 ∂Ψ

 ∂Ψ

∂Ψ
1 + 
II C +
III C C −1 − 
III C C − 2
∂ III C

 ∂ II C

 ∂ II C

(1.427)
Teniendo en consideración las relaciones (1.425) concluimos que:
 ∂Ψ
Ψ , b = 
 ∂I b
+

∂Ψ
∂Ψ
∂Ψ
b+
I b 1 −
III b b −1
∂ II b 
∂ II b
∂ III b
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.428)
Por: Eduardo W.V. Chaves
1 TENSORES
105
Haciendo una contracción por la izquierda con F y por la derecha por F T en la relación
(1.425) obtenemos que:
 ∂Ψ

∂Ψ
∂Ψ
∂Ψ
+
F ⋅ Ψ , C ⋅F T = 
I C  F ⋅ 1 ⋅ F T −
F ⋅C ⋅ F T +
III C F ⋅ C −1 ⋅ F T
∂
∂
∂
∂
I
I
I
I
I
I
I
I
C
C
C
 C

(1.429)
Y considerando las siguientes relaciones:
⇒ F ⋅1 ⋅ F T = F ⋅ F T = b
C = FT ⋅F
(1.430)
⇒ F ⋅C ⋅ F T = F ⋅ F T ⋅ F ⋅ F T = b ⋅ b = b2
C −1 = F −1 ⋅ b −1 ⋅ F
(1.431)
⇒ F ⋅ C −1 ⋅ F T = F ⋅ F −1 ⋅ b −1 ⋅ F ⋅ F T = b −1 ⋅ b
Luego, la expresión (1.429) puede ser reescrita como:
 ∂Ψ

∂Ψ
∂Ψ 2
∂Ψ
+
F ⋅ Ψ , C ⋅F T = 
b +
I C b −
III C b −1 ⋅ b
∂
∂
∂
∂
I
I
I
I
I
I
I
I
C
C
C
 C

 ∂Ψ


∂Ψ
∂Ψ
∂Ψ
= 
+
b+
I C 1 −
III C b −1  ⋅ b
∂ II C
∂ III C


 ∂I C ∂ II C
(1.432)
Teniendo en cuenta las relaciones (1.428) y (1.432) concluimos que:
 ∂Ψ


∂Ψ
∂Ψ
∂Ψ
F ⋅ Ψ , C ⋅F T = 
b+
I b 1 −
III b b −1  ⋅ b
+
∂ II b
∂ III b
 ∂I b ∂ II b 

= Ψ , b ⋅b
(1.433)
A través de la expresión (1.428) podemos concluir que la relación Ψ ,b ⋅ b = b ⋅ Ψ ,b es válida,
indicando que los tensores Ψ ,b y b son coaxiales.
Consideremos aún el tensor C dado por la expresión (1.420) a continuación vamos
obtener la derivada de la función Ψ = Ψ (C ) con respecto al tensor F :
Ψ,F =
∂Ψ (C ) ∂Ψ ∂C
=
:
∂C ∂F
∂F
(Ψ , F )kl
=
∂Ψ ∂C ij
∂C ij ∂Fkl
(1.434)
La derivada del tensor C con respecto a F viene a continuación:
∂C ij
∂Fkl
=
(
∂ Fqi Fqj
∂Fkl
) ∂(F )
=
qi
∂Fkl
Fqj + Fqi
( )
∂ Fqj
∂Fkl
= δ qk δ il Fqj + δ qk δ jl Fqi
(1.435)
= δ il Fkj + δ jl Fki
Luego, reemplazando (1.435) en (1.434) obtenemos:
(Ψ , F )kl = ∂Ψ (δ il Fkj + δ jl Fki ) = Fkj ∂Ψ
∂C ij
∂C lj
+ Fki
∂Ψ
∂C il
(1.436)
Debido a la simetría C lj = C jl y observando que i , j son índices mudos concluimos que:
(Ψ , F )kl
=2
∂Ψ
∂Ψ
Fkj = 2
Fkj
∂C lj
∂C jl
⇒
Ψ , F = 2Ψ , C ⋅ F T = 2 F ⋅ Ψ , C
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.437)
Por: Eduardo W.V. Chaves
106
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
Supongamos ahora que el tensor C sea dado por la relación C = UT ⋅ U = U ⋅ U = U 2 , donde
U es un tensor de segundo orden simétrico. Para obtener Ψ (C ) ,U podemos utilizar la
misma expresión obtenida en (1.437), es decir:
Ψ , U = 2Ψ , C ⋅ U = 2U ⋅ Ψ , C
(1.438)
Concluimos también que Ψ ,C y U son tensores coaxiales. Podemos generalizar lo
expuesto anteriormente como:
Sea un tensor de segundo orden simétrico A y una función escalar del tensor A ,
Ψ = Ψ (A ) , se cumple que:
Ψ , b = 2b ⋅ Ψ , A
para A = b T ⋅ b
Ψ , b = 2Ψ , A ⋅b para A = b ⋅ b T
Ψ , b = 2b ⋅ Ψ , A = 2Ψ , A ⋅b
= b ⋅ Ψ , A + Ψ , A ⋅b
para A = b ⋅ b y b = b T
(1.439)
1.7 Notación de Voigt
En el caso de que el tensor sea simétrico, puede resultar ventajoso trabajar solamente con
las componentes independientes del tensor. En el caso del tensor de segundo orden
simétrico, que tiene 6 componentes independientes, podemos representarlo en forma de
matriz columna:
 T11


Tij =  T12


 T13

T12
T22
T23
 T11 
T13 
T 

 22 

 T33 
→{T } =  
T23  Voigt

 T12 

 T23 
 
T33 
 T13 
(1.440)
Dicha notación la denotamos de Notación de Voigt. También, es posible representar un
tensor de segundo orden como:
E11


E ij = E12


E13

E12
E 22
E 23
 E11 
E13 
E 

 22 

 E 33 

→{E } = 
E 23  Voigt


 2E12 

 2E 23 


E 33 
 2E13 
(1.441)
Como visto anteriormente un tensor de cuarto orden, C , que presenta simetría menor,
C ijkl = C jikl = C ijlk = C jilk tiene 6 × 6 = 36 componentes independientes. Fijemos que
debido a simetría (ij ) tenemos 6 componentes independientes y debido a (kl ) también
tenemos 6 componentes independientes. En la notación de Voigt podemos representar
estas componentes en una matriz cuadrada 6 × 6 como:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
 C 1111
C
 2211
C
[C ] =  3311
 C 1211
C 2311

 C 1311
107
C1122
C1133
C 1112
C1123
C 2222
C 3322
C 2233
C 3333
C 2212
C 3312
C 2223
C 3323
C1222
C 2322
C1233
C 2333
C 1212
C 2312
C1223
C 2323
C1322
C1333
C 1312
C1323
C1113 
C 2213 
C 3313 

C1213 
C 2313 

C1313 
(1.442)
Verificamos también que, si además de simetría menor el tensor también presenta simetría
mayor C ijkl = C klij nos quedamos con 21 componentes independientes. Se puede
memorizar fácilmente el orden de las componentes en la matriz [C ] si tenemos en cuenta el
orden del tensor de segundo orden en notación de Voigt, i.e.:
 (11) 
(22)


 (33) 

 [(11) (22) (33) (12) (23) (13)]
 (12) 
(23) 


 (13) 
1.7.1
(1.443)
Tensores Identidad en Notación de Voigt
El tensor identidad de segundo orden será representado en la notación de Voigt como:
1
1
 
1 0 0 
1


Voigt
δ ij = 0 1 0 →{δ} =  
0 
0 0 1
0 
 
0
(1.444)
En el subapartado Tensores Identidad hemos definido 3 tensores identidades de cuarto orden
cuyas componentes son: I ijkl = δ ik δ jl , I ijkl = δ il δ jk y I ijkl = δ ij δ kl de los cuales solo
I ijkl = δ ij δ kl es simétrico. La representación de las componentes I ijkl = δ ij δ kl en la notación
de Voigt viene dada según la representación del tensor de cuarto orden dado por (1.442),
resultando:
I ijkl = δ ij δ kl
1
1

1
Voigt

→ I = 
0
0

0
[]
1 1 0 0 0
1 1 0 0 0
1 1 0 0 0
T
 = {δ}{δ}
0 0 0 0 0
0 0 0 0 0

0 0 0 0 0
(1.445)
donde I1111 = δ 11δ 11 = 1 , I1122 = δ 11δ 22 = 1 , etc.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
108
También hemos definido el tensor de cuarto orden simétrico I ijkl =
(
)
1
δ ik δ jl + δ il δ jk y su
2
representación en la Notación de Voigt viene dada por:
I ijkl
 I1111
I
 2211
I 3311
Voigt

→[I ] = 
 I1211
I 2311

 I1311
I1122
I 2222
I1133
I 2233
I1112
I 2212
I1123
I 2223
I1113  1

I 2213  0
I 3313  0
=
I1213  0
I 2313  0
 
I1313  0
I 3322
I1222
I 3333
I1233
I 3312
I1212
I 3323
I1223
I 2322
I1322
I 2333
I1333
I 2312
I1312
I 2323
I1323
1
0

0
=
0
0

0
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0

0 0 2 0 0
0 0 0 2 0

0 0 0 0 2
0 0 0 0 0
1 0 0 0 0 
0 1 0 0 0

0 0 12 0 0 
0 0 0 12 0 

0 0 0 0 12 
(1.446)
y la inversa:
[I ]−1
1.7.2
(1.447)
Producto Escalar en Notación de Voigt
r
El producto escalar entre un tensor de segundo orden simétrico T y un vector n viene
dado por:
r
r
b = T ⋅n
(1.448)
donde las componentes de esta operación son:
 b1   T11
b  =  T
 2   12
b 3   T13
T12
T22
T23
T13   n1   b1 = T11n1 + T12 n 2 + T13n 3

T23  n 2  ⇒ b 2 = T12 n1 + T22 n 2 + T23n 3
T33  n 3  b 3 = T13n1 + T23n 2 + T33n 3
(1.449)
Teniendo en cuenta la representación de un tensor de segundo en notación de Voigt, el
producto escalar (1.448) en la Notación de Voigt queda:
 T11 
T 
22
 b1  n1 0 0 n 2 0 n 3   

b  =  0 n
 T33 
0
0
n
n
2
2
1
3
  
 T 
b 3   0 0 n 3 0 n 2 n1   12 
144444244444
3  T23 
T
 
[N ]
 T13 
1.7.3
⇒
{b} = [N ] {T }
T
(1.450)
Leyes de Transformación en Notación de Voigt
Para un tensor de segundo orden, la ley de transformación de las componentes viene
definida de la forma:
Tij′ = Tkl a ik a jl
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.451)
Por: Eduardo W.V. Chaves
1 TENSORES
109
que explícitamente será:
 T11′
T ′
 12
 T13′
T12′
′
T22
′
T23
T13′   a11
′  =  a 21
T23
 
′   a 31
T33
a13   T11
a 23   T12
a 33   T13
a12
a 22
a 32
T12
T22
T23
T13   a11
T23  a 21
T33   a 31
a12
a 22
a 32
a13 
a 23 
a 33 
T
(1.452)
Efectuando la operación anterior, podemos reestructurarla en la notación de Voigt
resultando así que:
{T ′} = [M] {T }
donde:
 T11′ 
T′ 
 22 
T′ 
{T ′} =  33′  ;
 T12 
 T23
′ 
 
 T13′ 
(1.453)
 T11 
T 
 22 
T 
{T } =  33 
 T12 
 T23 
 
 T13 
(1.454)
y [M] es la matriz de transformación para las componentes de un tensor de segundo orden
cuando éstas están expresadas en Notación de Voigt, explícitamente [M] viene dada por:
 a11 2

2
 a 21
2

[M] =  a 31
 a 21 a11
a a
 31 21
 a 31 a11
a12 2
a13 2
2
2
a 22
a 32 2
a 22 a12
a 23
a 33 2
a13 a 23
a 32 a 22
a 32 a12
a 33 a 23
a 33 a13
2a11 a12
2a12 a13
2a 21 a 22
2a 31 a 32
(a11 a 22 + a12 a 21 )
2a 22 a 23
2a 32 a 33
(a13 a 22 + a12 a 23 )
(a 31 a 22 + a 32 a 21 ) (a 33 a 22 + a 32 a 23 )
(a 31 a12 + a 32 a11 ) (a 33 a12 + a 32 a13 )


2a 21 a 23


2a 31 a 33
 (1.455)
(a13 a 21 + a11 a 23 )
(a 33 a 21 + a 31 a 23 )
(a 33 a11 + a 31 a13 )
2a11 a13
Si la representación del tensor viene dada según (1.441), la representación de (1.451) en
notación de Voigt viene dada por:
{E ′} = [N ]{E }
(1.456)
donde
 a11 2

2
 a 21
2

[N ] =  a31
 2a 21 a11
 2a a
 31 21
 2a 31 a11
a12 2
a 22 2
a 32 2
2a 22 a12
2a 32 a 22
2a 32 a12
a13 2
a 23 2
a 33 2
2a13 a 23
2a 33 a 23
2a 33 a13
a11 a12
a 21 a 22
a 31 a 32
(a11 a 22 + a12 a 21 )
(a 31 a 22 + a 32 a 21 )
(a 31 a12 + a 32 a11 )
a12 a13
a 22 a 23
a 32 a 33
(a13 a 22 + a12 a 23 )
(a 33 a 22 + a 32 a 23 )
(a 33 a12 + a 32 a13 )

a11 a13

a 21 a 23


a 31 a 33

(a13 a 21 + a11 a 23 )
(a 33 a 21 + a 31 a 23 )
(a 33 a11 + a 31 a13 )
(1.457)
Las matrices (1.455) y (1.457) no son matrices ortogonales, i.e.
[N ]−1 ≠ [N ]T , pero se puede demostrar que se cumple que [N ]−1 = [M]T .
1.7.4
[M]−1 ≠ [M]T y
Representación Espectral en Notación de Voigt
Teniendo en cuenta la representación espectral del tensor T :
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
110
T=
3
∑T
a =1
a
nˆ ( a ) ⊗ nˆ ( a ) forma
 matricial
 → T = A T T ′ A
(1.458)
La expresión anterior puede ser reescrita como:
 T11
T
 12
 T13
T12
T22
T23
T13 
 T1

T 
T23  = A  0
T33 
 0
0 0
0 0

T 
0 0  A + A 0 T 2
0 0
0 0
0
0 0 0 

T 
0 A + A 0 0 0  A
0
0 0 T3 
(1.459)
ó
 T11
T
 12
 T13
T12
T22
T23
2
 a11
T13 

T23  = T1 a11 a12
a a
T33 
 11 13


+ T3  a 31 a 32
a a
 31 33
2
a 31
a11 a12
2
a12
a12 a13
a 31 a 32
2
a 32
a 32 a 33
2
 a 21
a11 a13 


a12 a13  + T2 a 21 a 22
2 
a a
a13

 21 23
a 21 a 22
2
a 22
a 22 a 23
a 21 a 23 

a 22 a 23 
2

a 23

a 31 a 33 

a 32 a 33 
2

a 33

(1.460)
Teniendo en cuenta que un tensor de segundo orden simétrico viene representado según
notación de Voigt por (1.440), la representación espectral de tensor viene dada por:
2
2
2
 a11

 a 21

 a 31

 T11 
 2 
 2 
 2 
T 
 a12 
 a 22 
 a 32 
 22 
2
2




 2 
T 
{T } =  33  = T1  a13  + T2  a 23  + T3  a33 
 a11 a12 
 a 21 a 22 
 a 31 a 32 
 T12 




a a 
 T23 
a a
a a
 12 13 
 22 23 
 32 33 
 
T
a
a
a
a
 13 
 11 13 
 21 23 
 a 31 a 33 
1.7.5
(1.461)
Tensor Desviador en Notación de Voigt
Teniendo en cuenta las componentes del tensor desviador:
Tijdev
 13 ( 2 T11 − T22 − T33 )

=
T12

T13

T12
1
3
(2 T22 − T11 − T33 )
T23


T23

1

(
2
−
−
)
T
T
T
33
11
22 
3
T13
(1.462)
La representación de Tijdev en notación de Voigt viene dada por:
 T11dev 
 2 − 1 − 1 0 0 0  T11 
 dev 
 − 1 2 − 1 0 0 0  T 
 T22 
  22 

 T33dev  1 − 1 − 1 2 0 0 0  T33 
 dev  = 
 
0
0 3 0 0  T12 
 T12  3  0
 T dev 
0
0
0 0 3 0  T23 

 23
 

0
0 0 0 3  T13 
 T13dev 
 0
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.463)
Por: Eduardo W.V. Chaves
1 TENSORES
111
r
Ejemplo 1.42: Considérese T ( x , t ) un tensor simétrico de segundo orden, el cual es
r
función de la posición ( x ) y del tiempo (t ) . Considérese también que las componentes del
tensor según la dirección x3 son iguales a cero, i.e. T13 = T23 = T33 = 0 .
r
NOTA: En el próximo subapartado definiremos T ( x , t ) como un campo tensorial, i.e. el
r
valor de T ( x , t ) depende de la posición y del tiempo. Como veremos más adelante, si el
r
r
tensor es independiente de una dirección para todo el dominio ( x ) , e.g. si T ( x , t ) es
independiente de la dirección x3 , ver Figura 1.32, el problema puede ser considerado como
bidimensional (estado plano) simplificando bastante las ecuaciones. ■
2D
x2
x2
T22
T22
T12
T12
T12
T11
T11
T11
x1
T12
T22
x3
x1
Figura 1.32: Problema bidimensional (2D).
′ , T12′ , tras un cambio de base en el plano x1 − x 2 tal
Obtener las componentes T11′ , T22
como se indica en la figura abajo
x2
x1′
x 2′
θ
x1
Obtener también el valor de θ correspondiente a las dirección principales de T .
OBS.: Utilizar notación de Voigt, y expresar los resultados en función de 2θ .
Solución:
Podemos utilizar directamente la ley de transformación obtenida en (1.453). En este caso
particular la matriz de transformación [M] , dada por (1.455), tras eliminar filas y columnas
asociadas con la dirección x3 queda:
 T11′   a11
T′  =  a 2
 22   21
 T12′   a 21 a11

2
a12
2
a 22
2
a 22 a12
  T11 
 
2a 21 a 22
  T22 
a11 a 22 + a12 a 21   T12 

2a11 a12
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
112
La matriz de transformación ( a ij ) en el plano viene dada en función de un único
parámetro, θ :
 cos θ sin θ 0
a ij = − sin θ cos θ 0

0
0
1
Resultando así que:
2
sin 2 θ
2 cos θ sin θ   T11 
 T11′   cos θ

 T ′  =  sin 2 θ
2
cos θ
− 2 sin θ cos θ   T22 
 22  
 T12′   − sin θ cos θ cos θ sin θ cos 2 θ − sin 2 θ   T12 


Tomando partido de las siguientes relaciones trigonométricas, 2 cos θ sin θ = sin 2θ ,
1 − cos 2θ
1 + cos 2θ
cos 2 θ − sin 2 θ = cos 2θ , sin 2 θ =
, cos 2 θ =
, obtenemos que:
2
2
 1 + cos 2θ   1 − cos 2θ 

 sin 2θ 
 

2
2

 
 T11′  
  T11 
+
−
1
cos
2
1
cos
2
θ
θ




T′  = 
 
 − sin 2θ   T22 
 
 22  
2
2

 
 T12′  
  T12 
 sin 2θ 
  − sin 2θ 
cos 2θ 


 

2 
 2 
Explícitamente las componentes vienen dadas por:

 1 + cos 2θ 
 1 − cos 2θ 
 T11 + 
 T22 + T12 sin 2θ
 T11′ = 
2
2






 1 + cos 2θ 
 1 − cos 2θ 
′ =
 T11 − 
 T22 − T12 sin 2θ
 T22
2
2






 sin 2θ 
 sin 2θ 
 T12′ =  −
 T11 + 
 T22 + T12 cos 2θ
2 

 2 

Reestructurando la expresión anterior aún podemos decir que:

 T11 + T22   T11 − T22 
+
 cos 2θ + T12 sin 2θ
 T11′ = 
2
2






 T + T22   T11 − T22 
′ =  11
−
 cos 2θ − T12 sin 2θ
 T22
2
2

 



 T − T22 
 T12′ = − 11
 sin 2θ + T12 cos 2θ

2


Recordemos que las direcciones principales se caracterizan por la ausencia de las
componentes tangenciales, es decir, Tij = 0 para i ≠ j . Si queremos encontrar las
direcciones principales en el caso plano hacemos que T12′ = 0 , obteniendo así:
 T − T22
T12′ = − 11
2

⇒

 sin 2θ + T12 cos 2θ = 0

2 T12
sin 2θ
=
cos 2θ T11 − T22
⇒
tg(2θ ) =
⇒
2 T12
T11 − T22
 T11 − T22

2

⇒
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)

 sin 2θ = T12 cos 2θ

1
2

2 T12
 T11 − T22
θ = arctg



Por: Eduardo W.V. Chaves
1 TENSORES
113
1.8 Campo de Tensores
r
r
Un Campo tensorial asocia a un tensor T ( x , t ) cada par ( x , t ) , es decir, que las componentes
r
r
de T ( x , t ) varían en el espacio x y en el tiempo t . El campo tensorial puede ser, escalar,
vector, o tensor de orden suprior:
Campo Escalar
r
φ = φ( x, t )
Notación simbólica
Notación indicial
(1.464)
r
φ = φ( x, t )
Campo Vectorial
Notación simbólica
Notación indicial
r r r
v = v ( x, t )
r
v i = v i ( x, t )
(1.465)
r
T = T ( x, t )
r
Tij = Tij ( x , t )
(1.466)
Campo Tensorial
Notación simbólica
Notación indicial
Como ejemplo de campo escalar, podemos mencionar el campo escalar de temperatura
r
r
T ( x , t ) donde en el tiempo t = t1 tenemos en cada punto del espacio ( x ) una temperatura
r
r r
T ( x , t1 ) , ver Figura 1.33(a). Otro ejemplo, podemos citar el campo de velocidades v ( x , t ) ,
r
ver Figura 1.33(b), donde en cada punto, en el tiempo t = t1 , está asociado un vector v .
x3
T5
T8
x3
t = t1
t = t1
r r
v ( x , t1 )
r
T4 ( x ( 4) , t1 )
T6
T3
T7
T1
x2
x2
T2
x1
x1
a) Campo escalar
b) Campo vectorial
Figura 1.33: Campo de tensores en el tiempo t1 .
r
Un Campo tensorial es continuo y diferenciable si las componentes de T ( x , t ) son funciones
continuas y diferenciables.
r
r
Si el campo tensorial es solo función de x , i.e. T = T ( x ) , decimos que el campo tensorial
r
es estacionario. Si el campo no es función x , T = T (t ) , decimos que el campo es homogéneo.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
114
1.8.1
Campo Escalar
r
Supongamos que tenemos una función escalar φ = φ( x ) (campo escalar) diferenciable de
forma continua, y por tanto existen ∂φ / ∂x1 , ∂φ / ∂x 2 y ∂φ / ∂x 3 y son continuas en el
r
r
espacio R 3 .Considerando ahora φ en un segundo punto, el cual es diferenciable ( x + dx ).
La diferencia de φ entre estos dos puntos llamamos de diferencial total de φ :
φ ( x1 + dx1 , x 2 + dx 2 , x3 + dx3 ) − φ ( x1 , x 2 , x3 ) ≡ dφ
(1.467)
Para cualquier función continua φ ( x1 , x 2 , x3 ) , dφ se relaciona linealmente con dx1 , dx 2 y
dx3 . Esta relación lineal viene dada por la regla de la cadena de diferenciación como:
dφ =
∂φ
∂φ
∂φ
dx1 +
dx 2 +
dx3
∂x1
∂x 2
∂x3
⇒
dφ = φ, i dxi
(1.468)
La diferenciación de las componentes de un tensor respecto a las coordenadas xi , se
expresa mediante el operador diferencial:
∂•
≡ •, i
∂xi
(1.469)
A continuación definiremos algunos operadores que nos ayudarán a manejar con los
campos tensoriales.
1.8.2
Gradiente
Gradiente de un escalar
El gradiente ∇ xr φ ó gradφ viene definido como:
r
∇ xr φ 
→ dφ = ∇ xr φ ⋅ dx
(1.470)
donde el operador ∇ xr denominamos operador nabla.
Expresando la definición (1.470) en la base cartesiana obtenemos que:
∂φ
∂φ
∂φ
dx1 +
dx 2 +
dx3 =
∂x1
∂x 2
∂x3
=
[
(∇ xr
φ) x eˆ 1 + (∇ xr φ) x eˆ 2 + (∇ xr φ) x eˆ 3
1
2
3
]⋅ [
( dx1 )eˆ 1 + (dx 2 )eˆ 2 + (dx3 )eˆ 3
]
(1.471)
Resolviendo el producto escalar anterior, hallamos:
∂φ
∂φ
∂φ
dx1 +
dx 2 +
dx3 = (∇ xr φ) x1 dx1 + (∇ xr φ) x2 dx 2 + (∇ xr φ) x3 dx3
∂x1
∂x 2
∂x 3
(1.472)
con lo que concluimos que la componentes de ∇ xr φ en coordenadas cartesianas son:
(∇ xr φ ) x1 =
∂φ
∂x1
;
(∇ xr φ) x2 =
∂φ
∂x 2
;
(∇ xr φ ) x3 =
∂φ
∂x 3
(1.473)
Podemos entonces definir el gradiente en términos de componentes como:
∇ xr φ =
∂φ ˆ
∂φ ˆ
∂φ ˆ
e1 +
e2 +
e3
∂x1
∂x 2
∂x3
(1.474)
El operador nabla ∇ xr queda definido como:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
∇ xr =
115
∂ ˆ
e i = ∂ , i eˆ i Operador Nabla
∂xi
(1.475)
Significado Geométrico de ∇ xr φ
ƒ
La dirección de ∇ xr φ es normal a la superficie φ = ctte . ∇ xr φ siempre apunta
(sentido) en la dirección creciente de φ , ver Figura 1.34.
ƒ
La magnitud de ∇ xr φ es la tasa de variación de φ con la distancia según esta
dirección.
OBS.: La superficie con φ = ctte (denominada superficie de nivel) es la superficie
formada por los puntos de mismo valor, es decir, al moverse por una superficie de
nivel el valor de la función no cambia.
r
Podemos decir que la normal a esta superficie φ = ctte será: n = ∇ xr φ . Entonces:
n̂ =
∇ xr φ
∇ xr φ
(1.476)
n̂
∇ xr φ
φ = ctte = c1
φ = ctte = c 2
φ = ctte = c3
Figura 1.34: Gradiente de φ .
r
El gradiente de un vector v :
r
r
grad( v ) ≡ ∇ xr v
(1.477)
Utilizando la definición de ∇ xr dada en (1.475), resulta:
r ∂ ( v i eˆ i )
∂v
∇ xr v =
⊗ eˆ j = ( v i eˆ i ) , j ⊗ eˆ j = v i , j eˆ i ⊗ eˆ j = i eˆ i ⊗ eˆ j
(1.478)
∂x j
∂x j
r
Con eso, definimos el gradiente de un campo tensorial (•( x , t )) en la base Cartesiana como:
∇ xr (•) =
∂(•)
⊗ ê j Gradiente de un campo tensorial en
∂x j
la base Cartesiana
(1.479)
Como podemos observar el gradiente de un vector (1.478) resulta ser un tensor de segundo
orden cuyas componentes v i, j explícitamente son:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
116
 ∂v 1

 ∂x1
∂v i  ∂v 2
=
=
∂x j  ∂x1

 ∂v 3
 ∂x1
v i, j
∂v 1 

∂x3 
∂v 2 
∂x3 

∂v 3 
∂x3 
∂v 1
∂x 2
∂v 2
∂x 2
∂v 3
∂x 2
(1.480)
Gradiente de un tensor de segundo orden T :
∇ xr T =
∂ (Tij eˆ i ⊗ eˆ j )
∂x k
⊗ eˆ k = Tij ,k eˆ i ⊗ eˆ j ⊗ eˆ k
(1.481)
y sus componentes son:
(∇ xr T )ijk
≡ Tij ,k
(1.482)
Ejemplo 1.43: Encuentre el gradiente de la función f ( x1 , x2 ) = sin( x1 ) + exp x1x2 en el punto
(0,1).
Solución:
Por definición el gradiente de una función escalar viene definido de la forma:
∇ xr f =
donde:
∂f ˆ
∂f ˆ
e1 +
e2
∂x1
∂x 2
∂f
= cos( x1 ) + x 2 exp x1x2
∂x1
[
;
]
∂f
= x1 exp x1x2
∂x 2
[
]
∇ xr f ( x1 , x 2 ) = cos( x1 ) + x 2 exp x1x2 eˆ 1 + x1 exp x1x2 eˆ 2
∇ xr f (0,1) = [2] eˆ 1 + [0] eˆ 2 = 2eˆ 1
r
⇒
r r
Ejemplo 1.44: Considérese un campo vectorial estacionario u = u( x ) . a) Obtener las
r r
r
componentes del diferencial total du . b) Considerando que u( x ) representa el campo de
desplazamientos y es independiente de la componente x3 , hacer la representación gráfica
del campo de desplazamiento en un elemento diferencial de área dx1 dx 2 .
Solución:
Según la definición de diferencial total y de gradiente se cumple que:
r r
u( x )
x2
r
x
r
dx
r
r
x + dx
r r
r
u( x + dx )
r r r
r r r
du ≡ u( x + dx ) − u( x )
r
r r
du = ∇ xr u ⋅ dx
x1
x3
Luego, las componentes vienen dadas por:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
du i =
∂u i
dx j
∂x j
⇒
 ∂u1

 du1   ∂x1
du  =  ∂u 2
 2   ∂x
 du 3   1
 ∂u 3
 ∂x1
117
∂u1
∂x 2
∂u 2
∂x 2
∂u 3
∂x 2
∂u1 

∂x3   dx 
1
∂u 2  

dx
2
∂x3  


∂u 3   dx3 
∂x3 
Explícitamente:

∂u1
∂u
∂u
dx1 + 1 dx 2 + 1 dx3
du1 =
∂x1
∂x 2
∂x3


∂u 2
∂u
∂u
dx1 + 2 dx 2 + 2 dx3
 du 2 =
∂x1
∂x 2
∂x3


∂u
∂u
∂u
du 3 = 3 dx1 + 3 dx 2 + 3 dx 3

∂x1
∂x 2
∂x3
con
du1 = u1 ( x1 + dx1 , x 2 + dx 2 , x3 + dx3 ) − u1 ( x1 , x 2 , x3 )

du 2 = u 2 ( x1 + dx1 , x 2 + dx 2 , x3 + dx3 ) − u 2 ( x1 , x 2 , x3 )
du = u ( x + dx , x + dx , x + dx ) − u ( x , x , x )
3
1
1
2
2
3
3
3
1
2
3
 3
Para el caso plano, es decir, cuando el campo es independiente de x3 , el campo de
desplazamientos en el elemento diferencial de área viene definido por:
∂u1
∂u1

du1 = u1 ( x1 + dx1 , x 2 + dx 2 ) − u1 ( x1 , x 2 ) = ∂x dx1 + ∂x dx 2

2
1

du = u ( x + dx , x + dx ) − u ( x , x ) = ∂u 2 dx + ∂u 2 dx
2
1
2
1
1
2
2
2
1
2
 2
∂x1
∂x 2
o aún:
∂u1
∂u1

u1 ( x1 + dx1 , x 2 + dx 2 ) = u1 ( x1 , x 2 ) + ∂x dx1 + ∂x dx 2

2
1

u ( x + dx , x + dx ) = u ( x , x ) + ∂u 2 dx + ∂u 2 dx
2
1
1
2
2
2
1
2
 2 1
∂x1
∂x 2
Observemos que la expresión anterior es equivalente a la expansión en serie de Taylor
teniendo en cuenta solo hasta términos lineales. La representación del campo de
desplazamiento en el elemento diferencial de área se muestra a continuación
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
118
u2 +
∂u 2
dx 2
∂x 2
u2 +
( x1 + dx1 , x 2 + dx 2 )
( x1 , x 2 + dx 2 )
u1 +
∂u
∂u 2
dx1 + 2 dx 2
∂x 2
∂x1
∂u1
dx 2
∂x 2
u1 +
r
du
dx 2
∂u
∂u1
dx1 + 1 dx 2
∂x 2
∂x1
u2 +
(u 2 )
( x1 + dx1 , x 2 )
( x1 , x 2 )
x2
∂u 2
dx1
∂x1
u1 +
(u1 )
∂u1
dx1
∂x1
dx1
x1
144444444444444444424444444444444444443
=
644444444444444444474444444444444444448
x 2 ,u 2
u2 +
∂u1
dx2
∂x2
∂u 2
dx2
∂x2
B′
B
B
dx 2
A′
O′
u2
A
O
dx1
+
dx 2
A′
O′
u1
u1 +
B′
A
∂u 2
dx1
∂x1
dx1
∂u1
dx1
∂x1
x1 ,u1
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
1.8.3
119
Divergencia
r
La Divergencia de un vector ( v ) será denotada por:
r
r
div ( v ) ≡ ∇ xr ⋅ v
(1.483)
r
r
r
r
div ( v ) ≡ ∇ xr ⋅ v = ∇ xr v : 1 = Tr (∇ xr v )
(1.484)
que por definición es igual a:
Luego:
[
][
r
r
∇ xr ⋅ v = ∇ xr v : 1 = v i , j eˆ i ⊗ eˆ j : δ kl eˆ k ⊗ eˆ l
= v i , j δ kl δ ik δ jl
]
= v k ,k
=
(1.485)
∂v 1 ∂v 2 ∂v 3
+
+
∂x1 ∂x 2 ∂x3
o aún:
[
][
= [v δ δ eˆ ]⋅ eˆ
= [v eˆ ]⋅ eˆ
∂[v eˆ ]
⋅ eˆ
=
r
r
∇ xr ⋅ v = ∇ xr v : 1 = v i , j eˆ i ⊗ eˆ j : δ kl eˆ k ⊗ eˆ l
i, j
kl
i ,k
i
i
i
lj
i
]
k
(1.486)
k
k
∂x k
Con lo que definimos que:
∇ xr ⋅ (•) =
∂ (•)
⋅ ê k Divergencia de (•) en la base
∂x k
Cartesiana
(1.487)
Podemos además verificar que la divergencia disminuye el orden de un tensor.
Divergencia de un tensor de segundo orden T
La divergencia de un tensor de segundo orden T es ∇ xr ⋅ T = ∇ xr T : 1 , lo que resulta ser un
vector:
∇ xr ⋅ T ≡ divT
=
=
∂(Tij eˆ i ⊗ eˆ j )
∂Tij
∂x k
⋅ eˆ k
δ jk eˆ i
(1.488)
∂x k
= Tik ,k eˆ i
NOTA: En este libro de texto, cuando estamos tratando con gradiente y divergencia de un
r
campo tensorial, e.g. ∇ xr v (gradiente de un campo vectorial), ∇ xr T (gradiente de un campo
tensorial de segundo orden), ∇ xr ⋅ T (divergencia de un campo de tensorial de segundo
r
orden), esto no indica que estamos haciendo una operación entre un vector ( ∇ xr ) y un
r
r
r
r
r
tensor, i.e. ∇ xr v ≠ (∇ xr ) ⊗ ( v ) , ∇ xr T ≠ (∇ xr ) ⊗ ( T ) , ∇ xr ⋅ T ≠ (∇ xr ) ⋅ ( T ) . En este libro, ∇ xr
indica un operador el cual debe ser aplicado a todo el campo tensorial, luego, el tensor debe
estar dentro del operador, ver expresiones (1.479) y (1.487). No obstante, es posible
r
relacionar ∇ xr v , ∇ xr T , ∇ xr ⋅ T con operaciones entre tensores, y es de fácil demostración
que se cumplen las siguientes relaciones:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
120
r
r
r
∇ xr v = ( v ) ⊗ (∇ xr )
r
∇ xr T = ( T ) ⊗ (∇ xr )
r
r
∇ xr ⋅ T = ( T ) ⋅ (∇ xr ) = (∇ xr ) ⋅ ( T T ) ■
(1.489)
A continuación definimos el operador Laplaciano ∇ xr 2 :
 ∂
2
∇ xr = ∇ xr ⋅ ∇ xr = 
 ∂xi

 ∂ ∂
 ∂

∂2

=
eˆ j  ⋅ eˆ i  =
δ
 ∂x j

 ∂xi ∂x j ij ∂xi ∂xi



(1.490)
∂2
∂2
∂2
∇ xr ≡ 2 + 2 + 2 = ∂, k ∂, k = ∂, kk
∂x1 ∂x 2 ∂x3
r
Luego, el Laplaciano de un vector ( v ) viene dado por:
r
r
2r
2r
∇ xr v = ∇ xr ⋅ (∇ xr v ) componente

s → ∇ xr v = [∇ xr ⋅ (∇ xr v )] = v i ,kk
2
[
]
i
(1.491)
i
Ejemplo 1.45: Probar la identidad:
r
r r
r
∇ xr ⋅ (a + b) = ∇ xr ⋅ a + ∇ xr ⋅ b
Solución:
r
r
Considerando que a = a j eˆ j y b = b k eˆ k y ∇ xr = ê i
∂
podemos expresar el primer
∂x i
miembro de la identidad como:
∂ (a j eˆ j + b k eˆ k )
∂x i
⋅ eˆ i
=
∂a j
∂x i
eˆ j ⋅ eˆ i +
r
r
∂b k
∂a
∂b
eˆ k ⋅ eˆ i = i + i = ∇ xr ⋅ a + ∇ xr ⋅ b
∂x i
∂x i ∂x i
c.q.d.
r
r
Ejemplo 1.46: Obtener las componentes de (∇ xr a) ⋅ b .
Solución:
r
r
Considerando: a = a j eˆ j ; b = b k eˆ k y ∇ xr = ê i
∂
( i = 1,2,3 ) podemos decir que:
∂x i

∂a j
∂a j
r r  ∂ (a j eˆ j )
 ∂a j

⊗ eˆ i  ⋅ (b k eˆ k ) = 
(∇ xr a) ⋅ b = 
eˆ j ⊗ eˆ i  ⋅ (b k eˆ k ) = b k δ ik
eˆ j = b k
eˆ j
 ∂x i

∂
x
∂
x
∂
x
k
i
 i



Resultando un vector. Expandiendo el índice mudo k obtenemos que:

∂a 1
∂a
∂a
+ b 2 1 + b3 1
 j = 1 ⇒ b1
∂x1
∂x 2
∂x 3


∂a j
∂a j
∂a j
∂a j
∂a
∂a
∂a

bk
= b1
+ b2
+ b3
⇒  j = 2 ⇒ b1 2 + b 2 2 + b 3 2
∂x k
∂x1
∂x 2
∂x 3
∂x1
∂x 2
∂x 3


 j = 3 ⇒ b ∂a 3 + b ∂a 3 + b ∂a 3
1
2
3

∂x1
∂x 2
∂x 3

Ejemplo 1.47: Probar que la siguiente relación es válida:
r
q 1 r r
1 r
∇ ⋅   = ∇ x ⋅ q − 2 q ⋅ ∇ xr T
T
T  T
r
x
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
r r
121
r
donde q( x , t ) es un campo vectorial arbitrario y T ( x , t ) es un campo escalar.
Solución:
r
r
q
∂  qi   qi 
1
1
1
1 r
∇ ⋅   =
  =   = q i ,i − 2 q i T,i = ∇ xr ⋅ q − 2 q ⋅ ∇ xr T
T
T
T
 T  ∂x i  T   T  ,i T
r
x
1.8.4
Rotacional
Rotacional de un vector
r
r
r
r
El rotacional de un vector v se representa por: rot ( v ) ≡ ∇ xr ∧ v , y viene definido en la
base Cartesiana por:
r
∂ ˆ
Rotacional de (•) en la base
e k ∧ (•)
∇ xr ∧ (•) =
∂x k
Cartesiana
(1.492)
Observemos que el rotacional es una operación entre tensores. Utilizando la definición de
producto vectorial entre vectores obtenemos el rotacional de un vector como:
r
r
r
∂v
∂v
∂ ˆ
e j ∧ ( v k eˆ k ) = k eˆ j ∧ eˆ k = k  ijk eˆ i =  ijk v k , j eˆ i
rot ( v ) = ∇ xr ∧ v =
∂x j
∂x j
∂x j
(1.493)
donde  ijk es el símbolo de permutación definido en (1.56) y donde hemos aplicado la
definición eˆ j ∧ eˆ k =  ijk eˆ i . También se puede obtener que:
eˆ 1
r
r
r
∂
rot ( v ) = ∇ xr ∧ v =
∂x1
v1
 ∂v
=  3
 ∂x 2
eˆ 2
∂
∂x 2
v2
∂v
− 2
∂x3
eˆ 3
∂
=  ijk v k , j eˆ i
∂x3
(1.494)
v3
 ∂v
 ∂v

∂v 
∂v 
eˆ 1 +  1 − 3 eˆ 2 +  2 − 1 eˆ 3
 ∂x1 ∂x 2 

 ∂x3 ∂x1 
r
Verifiquemos que la parte antisimétrica del gradiente del vector v , representado por
r anti
(∇ xr v ) ≡ W tiene como componentes:

0


 1  ∂v
∂v 
=   2 − 1 
 2  ∂x1 ∂x 2 
 1  ∂v
∂v 
  3 − 1 
 2  ∂x1 ∂x3 
1  ∂v 1 ∂v 3  


−
2  ∂x3 ∂x1  
r
1  ∂v 2 ∂v 3 


−
(∇ xr v ) anti ij ≡ v ianti
0
,j
2  ∂x3 ∂x 2 

1  ∂v 3 ∂v 2 
(1.495)


−

0
2  ∂x 2 ∂x3 

− w3 w2 
W12 W13   0
W12
W13   0
 0





= W21
− w1 
W23  =  − W12
0
W23  =  w3
0
0
 W31 W32
0   − W13 − W23
w1
0  − w2
0 
r
donde w1 , w2 , w3 son las componentes del vector axil w correspondiente al tensor
r
antisimétrico W ≡ (∇ xr v ) anti , ver subapartado 1.5.2.2.2. Tensor Antisimétrico.
[
]
1  ∂v 1 ∂v 2

−
2  ∂x 2 ∂x1



Si retomamos la definición del rotacional (1.494) y teniendo en consideración (1.495),
podemos decir que:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
122
r
r
r
 ∂v
 ∂v
 ∂v
∂v 
∂v 
∂v 
rot ( v ) = ∇ xr ∧ v =  3 − 2 eˆ 1 +  1 − 3 eˆ 2 +  2 − 1 eˆ 3
 ∂x1 ∂x 2 
 ∂x3 ∂x1 
 ∂x 2 ∂x3 
= 2W32 eˆ 1 + 2W13 eˆ 2 + 2W21eˆ 3
= 2(w1 eˆ 1 + w2 eˆ 2 + w3 eˆ 3 )
r
= 2w
(1.496)
Además si recurrimos a la identidad (1.143), podemos decir que se cumple que:
r r r
W⋅v = w ∧ v
r
r
1 r
= ∇ xr ∧ v ∧ v
2
(
)
(1.497)
Es interesante resaltar que la expresión anterior (1.497) podría haber sido obtenida a través
del Ejemplo 1.18, en el cual hemos demostrado que
r
r
1 r r
(a ∧ x ) es el vector axil asociado al
2
tensor antisimétrico ( x ⊗ a ) anti . Luego, el vector axil asociado al tensor antisimétrico
[
]
(
)
r anti
r
r
r
1 r
W = (∇ xr v ) anti = ( v ) ⊗ (∇ xr )
es el vector ∇ xr ∧ v .
2
Resumen
•
Divergencia
Gradiente
div (•) ≡ ∇ xr ⋅ •
grad(•) ≡ ∇ xr •
Escalar
Tensor
Escalar
Tensor
(2
r
rot (•) ≡ ∇ xr ∧ •
vector
Vector
ndo
Rotacional
Vector
orden)
Vector
(2ndo orden)
Tensor
Tensor
er
ndo
(3 orden)
(2
orden)
A continuación haremos algunas demostraciones de algunas identidades.
ƒ
r
r
r
r
r
r
(1.498)
rot (λa) = ∇ xr ∧ (λa) = λ (∇ xr ∧ a) + (∇ xr λ ∧ a)
r
r
El resultado de la operación ∇ xr ∧ (λa) será un vector, cuyas componentes vienen
dadas por:
[∇r
r
x
]
r
∧ (λa) i
=  ijk (λa k ) , j
=  ijk (λ , j a k + λa k , j )
=  ijk λa k , j  ijk λ , j a k
(1.499)
r
r
r
r
= λ (∇ x ∧ a) i  ijk (∇ x λ ) j a k
r
r
r
= λ (∇ xr ∧ a) i  (∇ xr λ ∧ a) i
r
r
r
r
r
r
con lo que comprobamos la identidad: rot (λa) = ∇ xr ∧ (λa) = λ(∇ xr ∧ a) + (∇ xr λ ∧ a) .
r r
r r
r
r r
r r
r r
(1.500)
ƒ
∇ xr ∧ (a ∧ b) = (∇ xr ⋅ b)a − (∇ xr ⋅ a)b + (∇ xr a) ⋅ b − (∇ xr b) ⋅ a
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
Las
componentes
del
producto
r r
(a ∧ b) k =  kij a i b j . Luego:
[∇r
r
x
123
r r
(a ∧ b )
vectorial
vienen
dadas
]
r r
∧ (a ∧ b) l =  lpk ( kij a i b j ) , p =  kij  lpk (a i , p b j + a i b j , p )
por
(1.501)
Considerando que  kij =  ijk , el resultado de  ijk  lpk = δ il δ jp − δ ip δ jl y reemplazando en la
expresión anterior obtenemos que:
[∇r
r
x
]
r r
∧ (a ∧ b) l =  kij  lpk (a i , p b j + a i b j , p )
= (δ il δ jp − δ ip δ jl )(a i , p b j + a i b j , p )
(1.502)
= δ il δ jp a i , p b j − δ ip δ jl a i , p b j + δ il δ jp a i b j , p − δ ip δ jl a i b j , p
= al , p b p − a p, p b l + al b p, p − a p b l , p
[
r
r
]
[
r r
]
[
r r
]
Podemos observar que (∇ xr a) ⋅ b l = a l , p b p , (∇ xr ⋅ a)b l = a p , p b l , (∇ xr ⋅ b)a l = a l b p , p ,
[
]
r r
(∇ xr b) ⋅ a l = a p b l , p .
r
r
r
r
2r
ƒ
∇ xr ∧ (∇ xr ∧ a) = ∇ xr (∇ xr ⋅ a) − ∇ xr a
Las
componentes
del
r
r
(∇ xr ∧ a) i =  ijk a k , j . Luego:
123
producto
(1.503)
vectorial
r
r
(∇ xr ∧ a)
vienen
dadas
por
ci
[∇r
r
x
]
r
r
∧ (∇ xr ∧ a) q =  qli c i ,l =  qli ( ijk a k , j ) ,l =  qli  ijk a k , jl
(1.504)
Considerando que  qli  ijk =  qli  jki = δ qj δ lk − δ qk δ lj , la expresión anterior queda:
[∇r
r
x
]
r
r
∧ (∇ xr ∧ a) q =  qli  ijk a k , jl
= (δ qj δ lk − δ qk δ lj )a k , jl
= δ qj δ lk a k , jl − δ qk δ lj a k , jl
(1.505)
= a k ,kq − a q ,ll
[
]
Podemos observar que [∇ xr (∇ xr ⋅ a)]q = a k , kq y ∇ xr 2 a q = a q ,ll .
r
ƒ
r
∇ xr ⋅ (ψ∇ xr φ ) = ψ∇ xr φ + (∇ xr ψ ) ⋅ (∇ xr φ)
2
(1.506)
∇ xr ⋅ (φ∇ xr ψ ) = (φψ ,i ) ,i
= φψ ,ii + φ ,i ψ ,i
(1.507)
= φ∇ xr ψ + (∇ xr φ ) ⋅ (∇ xr ψ )
2
donde φ y ψ son funciones escalares.
Otra identidad interesante que origina de la anterior es:
∇ xr ⋅ (φ∇ xr ψ ) = φ∇ xr ψ + (∇ xr φ ) ⋅ (∇ xr ψ )
2
∇ xr ⋅ (ψ∇ xr φ ) = ψ∇ xr φ + (∇ xr ψ ) ⋅ (∇ xr φ)
2
(1.508)
Restando las dos identidades anteriores obtenemos que:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
124
∇ xr ⋅ (φ∇ xr ψ ) − ∇ xr ⋅ (ψ∇ xr φ) = φ∇ xr ψ − ψ∇ xr φ
2
2
(1.509)
⇒ ∇ xr ⋅ (φ∇ xr ψ − ψ∇ xr φ ) = φ∇ xr ψ − ψ∇ xr φ
2
1.8.5
2
Campo Conservativo
r r
Un campo vectorial b( x , t ) se denomina conservativo si existe un campo escalar ( φ )
diferenciable tal que:
r
b = ∇ xr φ
(1.510)
r r
Si la función φ cumple la relación (1.510) decimos que φ es una función potencial de b( x , t ) .
r r
Un condición necesaria, pero no suficiente, para que b( x , t ) sea conservativo es que
r r
r
∇ xr ∧ b = 0 . En otras palabras, todo campo conservativo el rotacional es nulo, pero ni todo
rotacional nulo implica un campo conservativo.
Ejemplo 1.48: a) Probar que ∇ xr ⋅ (∇ xr ∧ v ) = 0 y que ∇ xr ∧ (∇ xr φ ) = 0 , donde φ es un
r
campo escalar, y v es un campo vectorial;
b) Demostrar que
r
r
r
r
r r
r r
r
r r
r
r
∇ xr ∧ (∇ xr ∧ v ) ∧ v = (∇ xr ⋅ v )(∇ xr ∧ v ) + ∇ xr (∇ xr ∧ v ) ⋅ v − (∇ xr v ) ⋅ (∇ xr ∧ v ) ;
r r
r
c) Teniendo en cuenta que ω = ∇ xr ∧ v , demostrar que
r
r
r
2r
2
2 r
∇ xr ∧ (∇ xr v ) = ∇ xr (∇ xr ∧ v ) = ∇ xr ω .
Solución:
r
r
Considerando: ∇ xr ∧ v =  ijk v k , j ê i
r
[
]
[
∇ xr
⋅ (∇ xr
r
)
]
r
∂
 ijk v k , j eˆ i
∧v =
∂x l
(
=  ijk
r
r
r
)⋅ eˆ
l
∂
∂
v k , j δ il =  ijk
vk , j
∂x l
∂x i
( )
( )
=  ijk v k , ji
r
La segunda derivada de v es simétrica en ij , i.e. v k , ji = v k ,ij , mientras que  ijk es
antisimétrico en ij , i.e.,  ijk = − jik , luego:
 ijk v k , ji =  ij1v1, ji +  ij 2 v 2, ji +  ij 3 v3, ji = 0
Observar que  ij1v1, ji es el doble producto escalar de un tensor simétrico con un
antisimétrico, cuyo resultado es cero.
Análogamente demostramos que:
r
r
∇ xr ∧ (∇ xr φ ) =  ijk φ , kj eˆ i = 0 i eˆ i = 0
NOTA: El rotacional del gradiente de un escalar resulta ser igual al vector nulo, y la
divergencia del rotacional de un vector resulta ser igual a cero.
r r
r
b) Denominamos por ω = ∇ xr ∧ v , con eso, quedamos con
[(
) ]
r
r
r
r r
r r
∇ xr ∧ ∇ xr ∧ v ∧ v = ∇ xr ∧ (ω ∧ v )
Recurrimos a la identidad (1.500), luego, se cumple que:
r
r r
r r
r r
r r
r r
∇ xr ∧ (ω ∧ v ) = (∇ xr ⋅ v ) ω − (∇ xr ⋅ ω)v + (∇ xr ω) ⋅ v − (∇ xr v ) ⋅ ω
r
r
r
Fijemos que el término ∇ xr ⋅ ω = ∇ xr ⋅ (∇ xr ∧ v ) = 0 , que fue demostrado en el apartado a).
Luego, concluimos que:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
125
r
r r
r r
r r
r r
∇ xr ∧ (ω ∧ v ) = (∇ xr ⋅ v )ω + (∇ xr ω) ⋅ v − (∇ xr v ) ⋅ ω
r
r
r r
r
r r
r
r
= (∇ xr ⋅ v )(∇ xr ∧ v ) + ∇ xr (∇ xr ∧ v ) ⋅ v − (∇ xr v ) ⋅ (∇ xr ∧ v )
[
c) Recurriendo a la identidad (1.503) podemos decir que:
]
r
r
r
r
2r
∇ xr v = ∇ xr (∇ xr ⋅ v ) − ∇ xr ∧ (∇ xr ∧ v )
r
r
r
= ∇ xr (∇ xr ⋅ v ) − ∇ xr ∧ ω
Aplicando el rotacional a la expresión anterior obtenemos que:
r
r
r
r
r
r
2r
∇ xr ∧ (∇ xr v ) = ∇ xr ∧ [∇ xr (∇ xr ⋅ v )] − ∇ xr ∧ (∇ xr ∧ ω)
14442r 444
3
=0
donde hemos tenido en cuenta que el rotacional del gradiente de un escalar resulta el vector
nulo. Recurrimos una vez más la identidad (1.503) para expresar el término
r
r
r
∇ xr ∧ (∇ xr ∧ ω) , resultando:
r
r
r
r
r
2r
2 r
∇ xr ∧ (∇ xr v ) = −∇ xr ∧ (∇ xr ∧ ω) = −∇ xr (∇ xr ⋅ ω) + ∇ xr ω
r
r
2 r
= −∇ xr ∇ xr ⋅ (∇ xr ∧ v ) + ∇ xr ω
1442443
=0
r
r
2
= ∇ xr (∇ xr ∧ v )
[
]
1.9 Teoremas con Integrales
1.9.1
Integración por Partes
La expresión de la integración por partes viene dada por:
b
∫ u( x)v′( x)dx = u( x)v( x)
b
a
b
∫ v( x)u ′( x)dx
−
a
donde v ′( x) =
a≤ x≤b.
1.9.2
(1.511)
a
dv
, y las funciones u (x) , v(x) tienen que ser diferenciables en el intervalo
dx
Teorema de la Divergencia
Dado un medio continuo B de volumen V , y contorno S , el teorema de la divergencia (o
r
teorema de Gauss) para un vector v está dado por:
∫
r
∇ xr ⋅ v dV =
V
∫
r
v ⋅ nˆ dS =
S
∫
r r
v ⋅ dS
∫v
S
i ,i
V
∫
∫
dV = v i nˆ i dS = v i dS i
S
(1.512)
S
donde n̂ es el vector unitario y exterior a la superficie S que contiene el volumen V en el
que está definido el campo vectorial.
Para un tensor de segundo orden:
∫
V
∇ xr ⋅ T dV =
∫
S
T ⋅ nˆ dS =
∫
S
r
T ⋅ dS
∫T
ij , j
V
∫
∫
dV = Tij nˆ j dS = Tij dS j
S
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(1.513)
S
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
126
S
n̂
x2
r
dS
dS
B
r
x
x1
x3
Figura 1.35.
Partiendo del teorema de la divergencia también podemos verificar que se cumplen las
siguientes relaciones:
∫ ( x ),
i
j
∫
∫
= δ ik xi nˆ j dS
= (δ ik xi ), j dV
dV
V
V
=
∫ [δ
S
ik , j x i
]
+ δ ik xi , j dV
V
∫
= x k nˆ j dS
(1.514)
S
∫
∫
= x k nˆ j dS
= x k , j dV
V
S
donde hemos considerado que δ ik , j = 0 ikj , y además considerando que x k , j = δ kj ,
obtenemos que:
δ kj ∫ dV = ∫ x k nˆ j dS
V
∫
Vδ kj = x k nˆ j dS
⇒
S
S
(1.515)
r
V 1 = x ⊗ nˆ dS
∫
S
También se cumple que:
∫ (x σ
i
jk
∫
∫
), k dV = ( xi σ jk ), k dV = xi σ jk nˆ k dS
V
V
=
S
∫ [x
i , k σ jk
∫ [δ
ik σ jk
]
=
V
∫
+ xi σ jk ,k dV = xi σ jk nˆ k dS
V
(1.516)
S
]
∫
+ xi σ jk ,k dV = xi σ jk nˆ k dS
S
Resultando que:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
∫x σ
i
jk , k
∫
∫
dV = xi σ jk nˆ k dS − σ ji dV
V
∫
127
S
V
(1.517)
r
r
x ⊗ (∇ xr ⋅ σ ) dV = x ⊗ (σ ⋅ nˆ ) dS − σ T dV
∫
V
∫
S
V
Queda de fácil demostración que se cumple que:
∫ (∇
r
x
V
r
r
⋅ σ ) ⊗ x dV = ∫ (σ ⋅ nˆ ) ⊗ x
∫
dS − σ dV
S
(1.518)
V
Ejemplo 1.49: Sea un dominio de área Ω delimitado por el contorno Γ como muestra
figura abajo:
n̂
Ω
x2
Γ
x1
r
r
Considérese también que m = m( x ) es un campo tensorial de segundo orden y ω = ω ( x )
es un campo escalar. Demostrar que se cumple la siguiente relación:
∫ [m : ∇
Ω
r
r
x (∇ x ω )
]dΩ = ∫ [(∇ xr ω ) ⋅ m] ⋅ nˆ dΓ − ∫ [(∇ xr ⋅ m) ⋅ ∇ xr ω ]dΩ
Γ
∫ [m
ij ω , ij
Ω
Ω
] dΩ = ∫ ( ω , m
i
ˆ dΓ −
ij )n j
Γ
∫ [m
ij , j ω , i
Ω
] dΩ
Solución: Se puede aplicar directamente la definición de integración por partes para la
demostración. Pero, partiremos de la definición del teorema de la divergencia, donde dado
r
un tensor v se cumple que:
∫∇
Ω
r
x
r
⋅v
dΩ =
r
∫ v ⋅ nˆ dΓ → Ω∫ v
Γ
indicial
j, j
∫
dΩ = v j nˆ j dΓ
Γ
r
r
Pero si consideramos que el tensor v es el resultante de la operación v = ∇ xr ω ⋅ m y lo
equivalente en notación indicial v j = ω , i m ij y reemplazándolo en la expresión anterior
obtenemos que:
∫v
Ω
j, j
∫
Γ
dΩ = v j nˆ j dΓ
⇒
⇒
⇒
∫ [ω,
Ω
i
∫Ω [ω,
ij
∫ [ω,
Ω
ij
m ij
]
,j
∫
dV = ω , i m ij nˆ j dΓ
Γ
]
∫
m ij + ω , i m ij , j dΩ = ω , i m ij nˆ j dΓ
]
∫
Γ
m ij dΩ = ω , i m ij nˆ j dΓ −
Γ
∫ [ω,
Ω
i
]
m ij , j dΩ
Lo equivalente en notación tensorial:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
128
∫Ω [m : ∇
r
r
x (∇ x ω )
]dΩ = ∫ [(∇ xr ω ) ⋅ m] ⋅ nˆ dΓ − ∫ [∇ xr ω ⋅ (∇ xr ⋅ m)]dΩ
Γ
c.q.d.
Ω
NOTA: Si consideramos ahora un dominio de volumen V delimitado por una superficie
r
S con normal n̂ y sea N un vector y T un escalar también se cumple que:
∫ N T,
i
ij
∫
∫
dV = N i T , i nˆ j dS − N i , j T , i dV
V
S
V
r
r
r
⇒ N ⋅ ∇ xr (∇ xr T )dV = (∇ xr T ⋅ N ) ⊗ n̂dS − ∇ xr T ⋅ ∇ xr NdV
∫
∫
V
∫
S
V
donde hemos aplicado directamente la definición de integración por partes.
1.9.3
Independencia del Camino
Una curva que conecta dos puntos A y B denominamos de camino de A a B . A
continuación, establecemos las condiciones con las cuales una integral de línea es
independiente del camino en una determinada región, ver Figura 1.36.
C1
B
r
dr
r
b
Si
∫
C1
A
x3
r r
r r
b ⋅ dr = b ⋅ dr
∫
C2
r
b - Campo conservativo
C2
x2
x1
Figura 1.36: Independencia del camino.
r
r
r
Luego, dado un campo vectorial b continuo, la integral ∫ b ⋅ dr es independiente del camino si
C
r
y solo si b es un campo conservativo. Como consecuencia, existe un campo escalar φ tal que
r
b = ∇ xr φ .
Con eso podemos concluir que:
B
∫
r r B
r
b ⋅ dr = ∇ xr φ ⋅ dr
∫
A
B
A
B
 ∂φ
r
∂φ ˆ  r
∂φ ˆ
(b1 eˆ 1 + b 2 eˆ 2 + b 3 eˆ 3 ) ⋅ dr = 
eˆ 1 +
e2 +
e 3  ⋅ dr
x
x
x
∂
∂
∂
1
2
3

A
A
∫
(1.519)
∫
Luego
b1 =
∂φ
∂x1
; b2 =
∂φ
∂x 2
; b3 =
∂φ
∂x3
(1.520)
Como el campo es conservativo el rotacional es cero:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
r r
r
∇ xr ∧ b = 0
eˆ 1
∂
∂x1
b1
⇒
eˆ 2
∂
∂x 2
b2
129
eˆ 3
∂
= 0i
∂x3
b3
(1.521)
Concluyendo que:
 ∂b 3 ∂b 2
−
=0

∂
∂
x
x
2
3

 ∂b1 ∂b 3
−
=0

 ∂x3 ∂x1
 ∂b 2 ∂b1
−
=0

 ∂x1 ∂x 2
 ∂b 3 ∂b 2
=

∂
∂x 3
x
2

 ∂b1 ∂b 3
⇒
=
 ∂x3 ∂x1
 ∂b 2 ∂b1
=

 ∂x1 ∂x 2
(1.522)
Luego, si no se cumple la condición anterior el campo no es conservativo.
1.9.4
Teorema de Kelvin-Stokes
r r
Sea una superficie regular S y sea un campo vectorial F( x , t ) .
Según el Teorema de Kelvin-Stokes:
r r
r
r
r
r
r
ˆ dS
r ∧ F ) ⋅ dS = ( ∇ r ∧ F ) ⋅ n
F
⋅
d
Γ
=
(
∇
∫
∫ x
∫ x
Γ
S
(1.523)
S
Si adoptamos un versor tangente al contorno Γ denominado por p̂ el teorema de Stokes
queda:
r
r
∫Γ F ⋅ pˆ dΓ = ∫ (∇
r
x
r
r
r
r
∧ F ) ⋅ dS = (∇ xr ∧ F) ⋅ nˆ dS
∫
S
(1.524)
S
n̂
x3
S
Ω
p̂
Γ
x2
x1
Figura 1.37: Teorema de Stokes.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
130
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
r
Representamos los vectores en la base cartesiana como F = F1eˆ 1 + F2 eˆ 2 + F3 eˆ 3 , el vector de
r
r
r
área como dS = dS1eˆ 1 + dS 2 eˆ 2 + dS 3 eˆ 3 , y dΓ = dx1eˆ 1 + dx 2 eˆ 2 + dx3 eˆ 3 . El rotacional de F
viene definido por:
eˆ 1
r
r
∂
∇ xr ∧ F =
∂x1
F1
eˆ 2
∂
∂x 2
F2
 ∂F
∂F
=  3 − 2
 ∂x 2 ∂x3
eˆ 3
∂
∂x3
F3
(1.525)

 ∂F
∂F
eˆ 1 +  1 − 3

 ∂x3 ∂x1

 ∂F
∂F
eˆ 2 +  2 − 1
 ∂x1 ∂x 2


eˆ 3

Con lo cual podemos expresar el teorema de Stokes en componentes como:
 ∂F
∂F
F1 dx1 + F2 dx 2 + F3 dx3 =  3 − 2
∂x 2 ∂x3
Γ
S
∫
∫
 ∂F

∂F
dS1 +  1 − 3
 ∂x 3 ∂x1


 ∂F
∂F
dS 2 +  2 − 1
 ∂x1 ∂x 2


dS 3

(1.526)
Como caso particular podemos tener que la superficie S coincide con el plano Ω como
muestra Figura 1.38, en este caso sigue siendo válida la expresión (1.526).
n̂
x3
Γ
Ω
x2
x1
Figura 1.38.
Otro caso particular es cuando la región Ω está toda contenida en el plano x1 − x 2 .
r
dS = dSê 3
x3
x2
Γ
ê3
Ω
x1
Figura 1.39: Teorema de Green.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
∫
131
r r
r
r
F ⋅ dΓ = (∇ xr ∧ F) ⋅ eˆ 3 dS
∫
Γ
(1.527)
Ω
Que es conocida como el teorema de Stokes en el plano o teorema de Green. En
componentes queda:
∫ F dx
Γ
1
1.9.5
1
 ∂F
∂F
+ F2 dx 2 =  2 − 1
∂x
∂x 2
Ω 1
∫

dS 3

(1.528)
Identidades de Green
r
Sea F un vector, aplicando el teorema de la divergencia obtenemos que:
∫
r
∇ xr ⋅ F dV =
V
r
F ⋅ nˆ dS
∫
(1.529)
S
Además, consideremos las identidades demostradas en (1.507) y (1.509), respectivamente:
∇ xr ⋅ (φ∇ xr ψ ) = φ∇ xr ψ + (∇ xr φ ) ⋅ (∇ xr ψ )
(1.530)
∇ xr ⋅ (φ∇ xr ψ − ψ∇ xr φ) = φ∇ xr ψ − ψ∇ xr φ
(1.531)
2
2
2
r
Considerando que F = φ∇ xr ψ y reemplazando (1.530) en (1.529) obtenemos que:
∫ φ∇
r
x
2
V
ψ + (∇ xr φ) ⋅ (∇ xr ψ) dV = ∫ φ∇ xr ψ ⋅ nˆ dS
S
⇒ (∇ xr φ) ⋅ (∇ xr ψ ) dV =
∫
∫ φ∇
V
r
x
S
(1.532)
ψ ⋅ nˆ dS − ∫ φ∇ xr ψ dV
2
V
que es conocida como la primera identidad de Green.
Si ahora reemplazamos (1.531) en (1.529) obtenemos que:
∫ φ∇
r
x
2
V
ψ − ψ∇ xr 2 φ dV = ∫ (φ∇ xr ψ − ψ∇ xr φ) ⋅ nˆ dS
(1.533)
S
que es conocida como la segunda identidad de Green.
r
r
r
Ejemplo 1.50: Si un vector se define como: b = ∇ xr ∧ v , probar que:
∫ λb nˆ
i
S
i
∫
d S = λ, i b i dV
V
r
r
donde λ es una función únicamente de x , i.e., λ = λ( x ) .
r
r
r
Solución: Si b = ∇ xr ∧ v , luego b i =  ijk v k , j . Reemplazando en la integral de superficie
anterior resulta:
∫ λb nˆ
i
S
i
∫
dS = λ ijk v k , j nˆ i dS
S
Aplicando el teorema de la divergencia de Gauss, resulta:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
132
∫ λb nˆ
i
S
i
∫
dS = λ ijk v k , j nˆ i dS
S
∫
= ( ijk λv k , j ), i dV
V
∫
= ( ijk λ, i v k , j +  ijk λv k , ji ) dV
V
∫
∫
= (λ, i  ijk v k , j + λ  ijk v k , ji ) dV = λ, i b i dV
1
424
3
1
424
3
c.q.d.
V
bi
V
0
1.10 Coordenadas Cilíndricas y Esféricas
Para la solución de determinados problemas, puede resultar conveniente emplear otros
sistemas de coordenadas, como por ejemplo el sistema de coordenadas cilíndricas o el
sistema de coordenadas esféricas.
1.10.1 Sistema de Coordenadas Cilíndricas
En el sistema de coordenadas cilíndricas ( r , θ, z ), se adopta como eje de simetría la
dirección z . En este sistema un punto P tiene coordenadas (r , θ, z ) , restringido a
0 ≤ θ ≤ 180º , donde estas variables están indicadas en la Figura 1.40.
Conversión de coordenadas cilíndricas a las coordenadas cartesianas:
 x1 = r cos θ

 x 2 = r sin θ
x = z
 3
(1.534)
Conversión de coordenadas cartesianas a las coordenadas cilíndricas
r = x 2 + x 2
1
2


x

2
θ = arctan
x
 1

 z = x3




(1.535)
Los versores en este sistema, eˆ r , eˆ θ , eˆ z pueden obtenerse con una simple ley de
transformación, donde la matriz de transformación viene dada por un giro alrededor del eje
z de un ángulo θ , es decir:
eˆ r   cos θ sin θ 0  eˆ 1 
ˆ  
 ˆ 
e θ  = − sin θ cos θ 0 e 2 
eˆ z   0
0
1  eˆ 3 
 
(1.536)
resultando
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
eˆ r = eˆ 1 cos θ + eˆ 2 sin θ
ˆ
e θ = −eˆ 1 sin θ + eˆ 2 cos θ
eˆ = eˆ
3
 z
133
eˆ 1 = eˆ r cos θ − eˆ θ sin θ
ˆ
e 2 = eˆ r sin θ + eˆ θ cos θ
eˆ = eˆ
z
 3
inversa
→
(1.537)
Podemos verificar en la ecuación (1.537) que ê r y ê θ son dependientes de θ , luego
podemos obtener las siguientes diferenciaciones:
∂eˆ r
= eˆ 1 (− sin θ) + eˆ 2 cos θ = eˆ θ
∂θ
∂eˆ θ
= −eˆ 1 (cos θ) + eˆ 2 (− sin θ) = −eˆ r
∂θ
(1.538)
x3
Proyección en el plano x1 − x 2
ê z
ê θ
r
x
r sin θ
ê r
r cos θ
θ
x2
r
z
θ
x2
r
x1
x1
Figura 1.40: Sistema de coordenadas cilíndricas.
Utilizando la regla de la cadena para derivadas parciales podemos demostrar que el
operador nabla ∇ se expresa en coordenadas cilíndricas como:
∇ = eˆ r
∂ ˆ 1 ∂ ˆ ∂
+ eθ
+ e3
∂r
∂x3
r ∂θ
(1.539)
El operador Laplaciano ∇ 2 en coordenadas cilíndricas queda:
∇2 =
∂2
1 ∂  ∂  1 ∂2
+
r  + 2
r ∂r  ∂r  r ∂θ 2 ∂x32
(1.540)
∂2 1 ∂
∂2
1 ∂2
= 2 +
+ 2
+
r ∂r r ∂θ 2 ∂x 32
∂r
La demostración de (1.540) siguen a continuación.

∂ ˆ 1 ∂ ˆ ∂  ˆ ∂ ˆ 1 ∂ ˆ ∂ 
 ⋅ er

+ eθ
+ e3
+ eθ
+ e3
∇ 2 = ∇ ⋅ ∇ =  eˆ r
r ∂θ
r ∂θ
∂x3   ∂r
∂x3 
 ∂r
(1.541)
Haciendo el producto y considerando que eˆ r ⋅ eˆ θ = eˆ θ ⋅ eˆ 3 = eˆ z ⋅ eˆ r = 0 , obtenemos los
siguientes términos:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
134
eˆ r
⋅
∂ ∂
∂2
∂  ˆ ∂ ˆ 1 ∂ ˆ ∂  ˆ ∂eˆ r ∂ ˆ ˆ ∂ ∂
 = e r ⋅
 e r
+ er ⋅ er
=
= 2
+ eθ
+ e3
∂r ∂r
∂r ∂r ∂r ∂r ∂r
r ∂θ
∂r  ∂r
∂x3 
{
(1.542)
eˆ θ
1ˆ
∂ 
∂ ˆ 1 ∂ ˆ ∂  1 ˆ ∂eˆ r ∂ 1 ˆ ˆ ∂ ∂
 = eθ ⋅
+ eθ ⋅ er
+
e θ ⋅  eˆ r
+ eθ
+ e3
r
r ∂θ
∂θ ∂r r
∂θ ∂r
∂θ  ∂r
∂x3  r
{
eˆ θ
(1.543)
1 ˆ ∂eˆ θ 1 ∂ 1 ˆ ˆ ∂ 1 ∂ 1 ∂
1 ∂2
+ eθ ⋅ eθ
=
+ 2
eθ ⋅
r
∂θ r ∂θ r
∂θ r ∂θ r ∂r r ∂θ 2
{
eˆ r
∂  ˆ ∂ ˆ 1 ∂ ˆ ∂  ∂2
er
=
+ eθ
+ e3
eˆ 3 ⋅
r ∂θ
∂x3  ∂r
∂x3  ∂x32
(1.544)
Sumando los términos obtenemos la expresión del Laplaciano dada por (1.540).
r
Consideremos un campo vectorial representado por v = v r eˆ r + v θ eˆ θ + v 3 eˆ 3 , a
continuación aplicaremos a este vector los siguientes operadores:
Rotacional de un vector
r
El rotacional de un vector v viene dado por:
eˆ r
r r
∂
∇∧v=
∂r
vr
eˆ θ
1 ∂
r ∂θ
vθ
eˆ 3
∂
∂x3
v3
(1.545)
Desarrollando el determinante anterior hallamos:
r r
 1 ∂v 3 ∂v θ
∇ ∧ v = eˆ r 
−
 r ∂θ ∂x 3
Divergencia

 ∂v
∂v
 − eˆ θ  3 − r
∂x3

 ∂r

1 ∂v r 
 ∂v
 + eˆ 3  θ −

r ∂θ 
 ∂r

(1.546)
r
La divergencia de un vector v en coordenadas cilíndricas viene dada por:
r 
∂ ˆ 1 ∂ ˆ ∂  ˆ
 ⋅ (e r v r + eˆ θ v θ + eˆ 3 v 3 )
∇ ⋅ v =  eˆ r
+ eθ
+ e3
r ∂θ
∂x3 
 ∂r
(1.547)
∂ ˆ
(e r v r + eˆ θ v θ + eˆ 3 v 3 ) + eˆ θ ⋅ 1 ∂ (eˆ r v r + eˆ θ v θ + eˆ 3 v 3 )
r ∂θ
∂r
∂ ˆ
(e r v r + eˆ θ v θ + eˆ 3 v 3 )
+ eˆ 3 ⋅
∂x3
r
⇒ ∇ ⋅ v = eˆ r
⋅
(1.548)
Operando los tres términos de la ecuación anterior separadamente obtenemos:
ƒ eˆ r ⋅
∂ ˆ
(e r v r + eˆ θ v θ + eˆ 3 v 3 )
∂r
Sabiendo que eˆ θ , eˆ 3 , v θ , v 3 no son dependientes de r :
∂ ˆ
eˆ r
⋅ (e θ v θ ) = eˆ r ∂ ⋅ (eˆ 3 v 3 ) = 0
∂r
∂r
Nos queda por definir:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
1 TENSORES
135
ˆ
∂ ˆ
ˆ r ⋅ eˆ r ∂v r + eˆ r ⋅ v r ∂e r = ∂v r
⋅ (e r v r ) = e1
eˆ r
2
3
∂r
∂r
∂r
∂r
{
1
0
ƒ eˆ θ ⋅
1 ∂ ˆ
(e r v r + eˆ θ v θ + eˆ 3 v 3 )
r ∂θ
Como eˆ 3 v 3 no es dependiente de θ , resulta:
1 ∂ ˆ
(e 3 v 3 ) = 0
eˆ θ ⋅
r ∂θ
Resultando:
∂v
∂eˆ
∂v
∂eˆ
1 ∂ ˆ
ˆ θ ⋅ eˆ r 1 r + eˆ θ ⋅ v r 1 r + eˆ θ ⋅ eˆ θ 1 θ + eˆ θ ⋅ v θ 1 θ
(e r v r + eˆ θ v θ ) = e1
eˆ θ ⋅
23 r ∂θ
∂θ
∂θ
r ∂θ
r{
r ∂θ
r{
=0
eˆ θ
= − eˆ r
144244
3
=0
1 1 ∂v θ
= vr +
r r ∂θ
∂ ˆ
(e r v r + eˆ θ v θ + eˆ 3 v 3 )
ƒ eˆ 3 ⋅
∂x3
∂v
∂v
∂ ˆ
ˆ 3 ⋅ eˆ 3 3 = 3
(e r v r + eˆ θ v θ + eˆ 3 v 3 ) = e1
eˆ 3 ⋅
2
3
∂x3
∂x3 ∂x3
=1
Teniendo en cuenta todas operaciones anteriores concluimos que:
r ∂v
1 1 ∂v θ ∂v 3
∇ ⋅ v = r + vr +
+
∂x3
r r ∂θ
∂r
(1.549)
r ∂v
∂v  ∂v
1
∇ ⋅ v = r + vr + θ  + 3
∂r
∂θ  ∂x 3
r
(1.550)
o bien:
1.10.2 Sistema de Coordenadas Esféricas
Las coordenadas esféricas ( r , θ, φ ) están indicadas en la Figura 1.41 luego, se cumple que:
Conversión de coordenadas esféricas a las coordenadas cartesianas:
 x1 = r sin θ cos φ

 x 2 = r sin θ sin φ
 x = r cos θ
 3
(1.551)
donde r ≥ 0 y 0 ≤ φ ≤ 180º y 0 ≤ θ ≤ 360º .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
136
x3
ê r
x3
θ
x1
r
ê θ
ê φ
x2
φ
x2
x1
Figura 1.41: Sistema de coordenadas esféricas.
Conversión de coordenadas cartesianas a las coordenadas esféricas:

r = x 2 + x 2 + x 2
1
2
3

2
 x + x2

2
 1
θ = arctan
x3



x
φ = arctan 2

x1




(1.552)
Los vectores unitarios eˆ r , eˆ θ , eˆ φ (mutuamente ortogonales entre sí) están ilustrados en la
Figura 1.41, y los podemos expresar en función de los versores eˆ 1 , eˆ 2 , eˆ 3 a través de una
transformación de coordenadas:
ƒ
Rotación según eje ê 3 de un ángulo φ
x3
Luego el nuevo sistema estará definido como:
 eˆ 1′   cos φ sin φ 0  eˆ 1 
ˆ  
 ˆ 
e ′2  = − sin φ cos φ 0 e 2 
eˆ ′3   0
0
1 eˆ 3 
 
ê 3
ê1
ê 2
ê′3
φ
ê′2
ê1′
x1
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
x2
1 TENSORES
ƒ
137
Rotación según eje ê ′2 de un ángulo β
x3
eˆ ′3′ = −eˆ θ
Pero podemos observar en la figura que:
β=
eˆ 1′′ = eˆ r
π
− θ luego cos β = sin θ y sin β = cos θ :
2
eˆ ′2′ = eˆ φ
θ
eˆ r   sin θ 0 cos θ  eˆ 1′ 
 
ˆ  
1
0  eˆ ′2 
e φ  =  0
eˆ θ   − cos θ 0 sin θ   eˆ ′3 
 
 
β
ê′3
ê1′
x2
ê′2
x1
Considerando las dos transformaciones anteriores podemos obtener que:
 eˆ r   sin θ 0 cos θ  cos φ sin φ 0  eˆ 1 
 
 ˆ  
1
0   − sin φ cos φ 0 eˆ 2 
 eφ  =  0
− eˆ θ  − cos θ 0 sin θ   0
0
1   eˆ 3 


 eˆ r   sin θ cos φ sin θ sin φ cos θ   eˆ 1 
ˆ  
 ˆ 
 e θ  = cos θ cos φ cos θ sin φ − sin θ e 2 
eˆ φ   − sin φ
cos φ
0   eˆ 3 
 
(1.553)
Explícitamente:
eˆ r = eˆ 1 cos φ sin θ + eˆ 2 sin φ sin θ + eˆ 3 cos θ
ˆ
e θ = eˆ 1 cos φ cos θ + eˆ 2 sin φ cos θ − eˆ 3 sin θ
eˆ = −eˆ sin φ + eˆ cos φ
1
2
 φ
(1.554)
La diferenciación de la base en función de θ , φ queda:
∂eˆ r
= eˆ 1 cos φ cos θ + eˆ 2 sin φ cos θ − eˆ 3 sin θ = eˆ θ
∂θ
∂eˆ r
= −eˆ 1 sin φ sin θ + eˆ 2 cos φ sin θ = eˆ φ sin θ
∂φ
∂eˆ θ
= −eˆ 1 cos φ sin θ − eˆ 2 sin φ sin θ − eˆ 3 cos θ = −eˆ r
∂θ
∂eˆ θ
= −eˆ 1 sin φ cos θ + eˆ 2 cos φ cos θ = eˆ φ cos θ
∂φ
∂eˆ φ
= −eˆ 1 cos φ − eˆ 2 sin φ = −eˆ r sin θ − eˆ θ cos θ
∂φ
(1.555)
(1.556)
(1.557)
(1.558)
(1.559)
El operador nabla será dado por:
∇ = eˆ r
∂ ˆ 1 ∂ ˆ
1
∂
+ eθ
+ eφ
∂r
r ∂θ
r sin θ ∂φ
(1.560)
El operador Laplaciano ∇ 2 en coordenadas esféricas queda:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
138
∇2 =
∂ 
∂ 
∂2
1 ∂  2 ∂ 
1
1
r
θ
+
+
sin




∂θ  r 2 sin 2 θ ∂φ 2
r 2 ∂r  ∂r  r 2 sin θ ∂θ 
∂2
2 ∂
1 ∂2
cotg θ ∂
1
∂2
= 2 +
+ 2
+
+
r ∂r r ∂θ 2
r 2 ∂θ r 2 sin 2 θ ∂φ 2
∂r
(1.561)
Divergencia
r
La divergencia de un vector v en coordenadas esféricas viene dada por:
r 
1
∂ ˆ 1 ∂ ˆ
∂  ˆ
 ⋅ (e r v r + eˆ θ v θ + eˆ φ v φ )
∇ ⋅ v =  eˆ r
+ eθ
+ eφ
r ∂θ
r sin θ ∂φ 
 ∂r
(1.562)
Haciendo el producto obtenemos:
∂v φ 2
r ∂v
∂v
∇⋅v = r + θ +
+ v r + v φ cotg θ
∂θ
∂φ r
∂r
(1.563)
Ejemplo 1.51: Escribir la ecuación ( z = x 2 − y 2 ), dada en coordenadas cartesianas, en
coordenadas cilíndricas y esféricas:
Solución:
cilíndricas: z = (r cos θ)2 − (r sin θ)2 ⇒ z = r 2 cos(2θ )
esféricas: r cos θ = (r sin θ cos φ )2 − (r sin θ sin φ )2
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
A. Representación gráfica de un tensor
´
Apendice
A
´ Grafica
´
Representacion
de
un Tensor
A.1 Introducción
Existen diversas aplicaciones prácticas en Ingeniería que utiliza la representación gráfica de
un tensor de segundo orden. La representación gráfica de un tensor de segundo orden
consiste en una gráfica bidimensional donde la abscisa viene representada por la
componente normal ( T N ) y la ordenada por la componente tangencial ( TS ) para todos los
planos admisibles, nˆ ⋅ nˆ = 1 .
A.2 Proyección de un Tensor de Segundo Orden
sobre una Dirección
A.2.1 Componente Normal y Tangencial
Como hemos visto en el capítulo 1, la proyección de un tensor de segundo ( T ) orden
r ˆ
sobre una dirección ( n̂ ) resulta un vector t (n) = T ⋅ nˆ .
r
ˆ
El vector t (n) asociado a la dirección n̂ puede descomponerse en una componente normal
r
r
T N (vector normal) y en otra tangencial TS (vector tangencial) tal como se indica en la
Figura A.1. La suma vectorial de estos vectores resulta:
r
r
r ˆ
t (n ) = T N + T S
(A.1)
Siendo n̂ el versor normal al plano y ŝ el versor tangente al plano, podemos escribir la
relación anterior como:
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
140
donde T N
r ˆ
t (n ) = T N nˆ + TS sˆ
r
r
y TS son los módulos de T N y de TS , respectivamente.
(A.2)
r ˆ
t (n)
x3
r
TS
r
TN
ŝ
n̂
P
ê 3
ê1
ê 2
x2
x1
Figura A.1: Componentes normal y tangencial del vector.
r
Escribiendo el vector T N en función de su módulo T N y del versor n̂ , las siguientes
relaciones son válidas:
r
TN
= T N nˆ ≡ T N ⊗ nˆ
r ˆ
r ˆ
= (t (n) ⋅ nˆ ) nˆ = (nˆ ⋅ t (n) ) nˆ
[
r
TN i
= T N nˆ i
ˆ
ˆ
= (t (kn) nˆ k ) nˆ i = (nˆ k t (kn) ) nˆ i
]
[
ˆ nˆ
=1
nˆ4
⋅2
T4
⋅ n3
]
= nˆ k Tkj nˆ j nˆ i
1424
3
TN
(A.3)
TN
Verificamos que T N puede ser obtenido a través de las siguientes relaciones:
r ˆ
T N = t (n) ⋅ nˆ = nˆ ⋅ T ⋅ nˆ = nˆ k Tkj nˆ j
(A.4)
r
Observemos que T será un tensor definido positivo si T N = nˆ ⋅ T ⋅ nˆ > 0 para todo nˆ ≠ 0 .
Podemos concluir también que T N = nˆ ⋅ T ⋅ nˆ = nˆ ⋅ T sym ⋅ nˆ luego, si la parte simétrica del
tensor es un tensor definido positivo el tensor también lo será.
r
Análogamente, podemos representar el vector TS en función de su módulo TS y del
versor ŝ :
r
TS
r
TS i
= TS sˆ
r ˆ
r ˆ
= (t (n) ⋅ sˆ )sˆ = (sˆ ⋅ t (n) )sˆ
[
= TS sˆ i
ˆ
= (t (jn) sˆ j )sˆ i
[
]
=1
sˆ4
⋅2
T4
⋅3
nˆ sˆ
]
= T jk nˆ k sˆ j sˆ i
1424
3
TS
(A.5)
TS
Otra forma de obtener el vector tangencial puede ser a través de la ecuación (A.1):
r
r
r ˆ
TS = t (n) − T N = T ⋅ nˆ − T : (nˆ ⊗ nˆ ) nˆ
(A.6)
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
[
]
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
141
r
r
r
Ya que TS y T N son perpendiculares. También podemos obtener el módulo de TS a
través del teorema de Pitágoras:
ˆ
ˆ
TS2 = t (i n) t (i n) − T N2
r
ˆ
con t (n)
2
ˆ
(A.7)
ˆ
= t (i n) t (i n) = Tij Tik nˆ j nˆ k .
A.2.2 Máxima y Mínima Componente Normal
Como visto anteriormente la componente normal viene dada por T N = nˆ ⋅ T ⋅ nˆ con la
restricción que nˆ ⋅ nˆ = 1 (versor). Los valores de máximos y mínimos de T N con restricción
pueden ser obtenidos a través del método del multiplicador de Lagrange. Este método
consiste en construir una función tal que:
L(nˆ , µ) = T N − µ(nˆ ⋅ nˆ − 1) = nˆ ⋅ T ⋅ nˆ − µ(nˆ ⋅ nˆ − 1)
(A.8)
r
r
∂L (nˆ , µ)
= 2 T sym ⋅ nˆ − 2µnˆ = 0
⇒
( T sym − µ1) ⋅ nˆ = 0
∂nˆ
∂L (nˆ , µ) ˆ ˆ
= n ⋅ n − 1 = 0 ⇒ nˆ ⋅ nˆ = 1
∂µ
(A.9)
donde µ es el multiplicador de Lagrange. Diferenciando la función L(nˆ ) con respecto a n̂
y a µ obtenemos el siguiente sistema de ecuaciones:
El primer sistemas de ecuaciones sólo tiene solución si y solo si det ( T sym − µ1) = 0 que es
el problema de autovalor de la parte simétrica de T . Es decir, los valores de máximos y
mínimos de T N corresponden a los autovalores de T sym . Siendo T1sym , T2sym , T3sym , los
autovalores de T sym , reestructuramos los autovalores de tal forma que:
TIsym > TIIsym > TIIIsym
(A.10)
Podemos entonces decir que el valor máximo de T N es TIsym , y TIIIsym es el valor mínimo.
NOTA: Ya era de esperar que los valores extremos de T N estuviera relacionado con el
tensor simétrico T sym ya que para la obtención de T N la parte antisimétrica no juega
ningún papel T N = nˆ ⋅ T ⋅ nˆ = nˆ ⋅ T sym ⋅ nˆ .
OBS.: Cuando utilizamos la nomenclatura TI , TII , TIII ya está implícito que
TI > TII > TIII .
A.2.3 Máxima y Mínima Componente Tangencial de un
Tensor Simétrico
Por simplicidad vamos trabajar en el espacio principal del tensor T y vamos considerar que
el tensor es simétrico, T = T T . En el espacio principal, las componentes del tensor T
vienen representadas por las componentes normales (Figura A.2), ya que en este espacio
carece de componentes tangenciales. Observemos también que en este espacio las
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
142
ˆ
componentes normales Ti tienen las mismas direcciones que t i(n) . El módulo de la
componente normal T N en un plano arbitrario de normal n̂ , según la expresión (A.4),
viene dado por la expresión:
ˆ
T N = t i(n) n i = Tij n j n i = T1n12 + T2 n 22 + T3 n 32
(A.11)
Observemos que para el plano particular n i = [1,0,0] ⇒ T N = T1 . Geométricamente (teorema
de Pitágoras), podemos obtener el módulo de la componente tangencial:
r ˆ
TS2 = t (n)
2
ˆ
ˆ
− T N2 = t i(n) t i(n) − T N2 = Tij Tik nˆ j nˆ k − T N2
x 3′
(A.12)
x 3′
r ˆ
t (n)
T3
r
TN
r
TS
T2
n̂
x ′2
x ′2
T1
plano arbitrario
x1′
x1′
Figura A.2: Componentes del tensor en el espacio principal.
Reemplazando la ecuación (A.11) en la ecuación (A.12) hallamos:
(
TS2 = T12 nˆ 12 + T22 nˆ 22 + T32 nˆ 32 − T1nˆ 12 + T2 nˆ 22 + T3nˆ 32
)
2
(A.13)
Podemos formular la siguiente pregunta: ¿Cuáles son los valores de n̂ i que hacen máximo
la función TS2 ? Este problema se reduce a encontrar valores extremos de la función:
F (nˆ ) = TS2 − µ(nˆ i nˆ i − 1)
(A.14)
donde µ es el multiplicador de Lagrange, con la restricción n i n i = 1 .
La condición necesaria es:
∂F (nˆ )
=0
∂n i
resultando:
{
nˆ {T
nˆ {T
;
(
− 2 T (T nˆ
− 2 T (T nˆ
∂F (nˆ )
=0
∂µ
) }
+ T nˆ ) + µ}= 0
+ T nˆ ) + µ}= 0
(A.15)
nˆ 1 T12 − 2 T1 T1 nˆ 12 + T2 nˆ 22 + T3 nˆ 32 + µ = 0
2
2
2
3
2
3
2
1
2
1
+ T2 nˆ 22
3
1
2
1
+ T2 nˆ 22
3
2
3
3
2
3
(A.16)
con la condición nˆ i nˆ i = 1 . Podemos obtener analíticamente la solución del sistema anterior
resultando en las siguientes soluciones posibles:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
solución
n̂1
n̂ 2
n̂ 3
TS
(1)
±1
0
0
TS = 0
(2)
0
±1
0
TS = 0
(3)
0
0
±1
TS = 0
(4)
±
0
(5)
1
±
(6)
±
2
±
0
2
1
±
1
±
2
1
(A.17)
T2 − T3
2
T − T3
TS = ± 1
2
1
TS = ±
2
1
2
TS = ±
0
2
143
T1 − T2
2
Los valores de TS fueron obtenidos introduciendo los valores de n̂ i en la expresión (A.13).
Los tres primeros conjuntos de soluciones nos proporcionan los valores mínimos de TS ,
que corresponden justamente con las direcciones principales.
Para las soluciones (4) los planos de máximo relativo para TS están esquematizados en la
Figura A.3.
T3
[
nˆ i = 0
1
2
1
2
T3
]
[
nˆ i = 0 −
1
2
1
2
T2
T2
[
nˆ i = 0 −
T1
1
2
−
1
2
]
]
[
nˆ i = 0
T1
−
1
2
1
2
]
Figura A.3: Planos de máxima componente tangencial (relativa) con n1 = 0 .
Para las soluciones (5), los planos están esquematizados en la Figura A.4.
T3
T3
nˆ i =
[
1
2
0
1
2
[
nˆ i = −
]
1
2
1
2
0
T2
T2
T1
[
nˆ i = −
1
2
0 −
1
2
]
]
T1
nˆ i =
[
1
2
0 −
1
2
]
Figura A.4: Planos de máxima componente tangencial (relativa) con n 2 = 0 .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
144
En la Figura A.5 podemos visualizar los planos de máxima componente tangencial para las
soluciones (6).
T3
T3
nˆ i =
[
1
2
0
1
2
[
]
nˆ i = −
nˆ i =
[
1
2
−
1
2
0
1
2
1
2
[
nˆ i = −
1
2
−
1
2
0
]
]
T2
T2
T1
0
]
T1
Figura A.5: Planos de máxima componente tangencial (relativa) con n 3 = 0 .
Ordenando los autovalores (valores principales) ( T1 , T2 , T3 ) de la forma:
TI > TII > TIII
(A.18)
obtenemos el máximo absoluto de la tensión de corte:
TS max =
TI − TIII
2
(A.19)
A.3 Representación Gráfica de un Tensor de
Segundo Orden Arbitrario
Conocidas las componentes de un tensor de segundo orden en la base cartesiana Tij
podemos obtener las componentes normales y tangenciales ( TN , TS ) para cualquier plano
de normal n̂ , con la restricción nˆ ⋅ nˆ = 1 , en componentes nˆ 12 + nˆ 22 + nˆ 32 = 1 . Podemos
dibujar una gráfica donde la abscisa viene representa por la componente normal ( TN ) y la
ordenada por la componente tangencial ( TS ) al plano.
En este apartado utilizaremos un procedimiento numérico, es decir, de forma aleatoria
sacamos distintos valores (posibles) para la normal (versor) y obtenemos los valores
correspondientes de ( TN , TS ) y plotamos sus coordenadas en una gráfica T N × TS . De esta
forma vamos obtener la representación gráfica del tensor de segundo orden, es decir, los
valores posibles (factibles) para la componente normal y tangencial del tensor en cada
plano. De igual manera también dibujamos la gráfica correspondiente a la parte simétrica
del tensor, ( T N( sym ) = T N ) × TS( sym ) .
A continuación adoptamos algunos valores para las componentes del tensor y verificamos
que formato tiene la gráfica componente normal versus componente tangencial.
El primer ejemplo, ver Figura A.6, constituye de un tensor no simétrico. Es interesante
r
observar que el tensor es definido positivo ya que T N = nˆ ⋅ T ⋅ nˆ > 0 para todo nˆ ≠ 0 .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
145
Verifiquemos también que el tensor tiene tres autovalores reales, y por definición de
autovalor, corresponden cuando TS = 0 . Los valores máximos y mínimos para la
componente T N son coincidentes con los autovalores de la parte simétrica de T .
Para la componente tangencial podemos hacer la siguiente descomposición:
] [
]
r
TS = 1
sˆ4
⋅2
T4
⋅3
nˆ sˆ = sˆ ⋅ T sym ⋅ nˆ + sˆ ⋅ T anti ⋅ nˆ sˆ
[
(A.20)
TS
Cuando n̂ sea una de las direcciones principales de la parte simétrica, tenemos que:
[
] [
] [
]
r
TS = sˆ ⋅ T sym ⋅ nˆ + sˆ ⋅ T anti ⋅ nˆ sˆ = sˆ ⋅ λnˆ + sˆ ⋅ T anti ⋅ nˆ sˆ = sˆ ⋅ T anti ⋅ nˆ sˆ
(A.21)
ya que los versores ŝ , n̂ son ortogonales, sˆ ⋅ nˆ = 0 . Esto implica que en los planos n̂ (1) ,
n̂ ( 2 ) , n̂ (3) , (autovectores de T sym ), las correspondientes componentes normales y
tangenciales asociadas al tensor T vendrán dadas por el autovalor de T sym , y componente
tangencial dada por:
r nˆ )
r nˆ )
r nˆ )
TS = sˆ ⋅ T anti ⋅ nˆ = sˆ ⋅ t (anti
= ± t (anti
sˆ ⋅ sˆ = ± t (anti
(A.22)
5 3 1 
Tij = 1 4 2
3 6 6
TS
T N max = 10,55; TS = 2,424
T N min = 0,84; TS = 2,41
TIII = 1,52
TII = 3,59
T N min = 0,84; TS = −2,41
TI = 9,89
TN
T N max = 10,55; TS = −2,424
TSsym
TSsym max = 4,86
Tijsym
TIsym
= 0,84
II
TIsym
= 3,61
I
5 2 2
= 2 4 4
2 4 6
TIsym = 10,55
TN
Figura A.6: Representación gráfica de un tensor definido positivo no simétrico.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
146
Por ejemplo, para el autovalor
nˆ (j1)
TIsym = 10,55
que está asociado al autovector
= [− 0,45229371;−0,561517458;−0,692913086] , tenemos que:
 0 1 − 1   − 0,45229371 
r (nˆ )
TS = ± t anti = ±  − 1 0 − 2  − 0,561517458 = ±
 1 2 0   − 0,692913086
1
44244
3 1442444
3
Tijanti
 0,1313956 
 1,8381199  = ±2,424378


 − 1,5753286
(A.23)
nˆ (j1)
Para el autovalor TIsym
= 3,61 tenemos que:
I
 0 1 − 1   0,88542667 
r (nˆ )
TS = ± t anti = ±  − 1 0 − 2  0,18949182  = ±
 1 2 0  0,42439659
 − 0,234905 
 0,036633496  = ±0,55947


 − 0,50644304
(A.24)
= 0,84 tenemos que:
Para el autovalor TIsym
II
 0 1 − 1   0,107004733 
r (nˆ )
TS = ± t anti = ±  − 1 0 − 2 − 0,80547563 = ±
 1 2 0   0,582888489 
 − 1,3883641
 − 1,2727817  = ±2,41


 − 1,5039465 
(A.25)
Debemos enfatizar que este procedimiento sólo es válido para los planos correspondientes
a los autovectores de la parte simétrica de T , para un plano arbitrario ya no es válido.
Con lo que respecta a la parte simétrica del tensor, verifiquemos que el valor máximo y
mínimo de la componente normal se encuentra en los valores principales,
T N max = T Isym = 10,55 y T N min = TIsym
= 0,84 . La máxima componente tangencial es igual al
II
radio del círculo que forma TIsym = 10,55 y TIsym
= 0,84 , ver Figura A.6, resultando
II
TSsym max =
10,55 − 0,84
= 4,86 .
2
El segundo ejemplo se trata de un tensor simétrico, ver Figura A.7. Además podemos
verificar que el tensor no es definido positivo. Intuitivamente nos indica que para un tensor
simétrico la gráfica componente normal versus componente tangencial es la intersección de
tres circunferencias. Podemos verificar también en esta gráfica que la componente
tangencial máxima viene dada por TS max =
TI − TIII
2
=
8,328 − (−0,78)
= 4,55 .
2
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
147
TS
TS max = 4,55
1 2 3
Tij = 2 4 2
3 2 5
TIII = −0,78
TII = 2,454
TI = T N max = 8,328
TN
Figura A.7: Representación gráfica de un tensor simétrico.
El tercer ejemplo trata de un tensor simétrico que tiene dos autovalores iguales. Podemos
verificar que los valores posibles para ( TN , TS ) está limitado a la circunferencia de radio
R=
TI − TIII
T + TIII
= 2,5 y centrada en el punto ( T N = I
= 1,5 , TS = 0 ), ver Figura A.8.
2
2
Intuitivamente nos lleva a pensar que la representación gráfica de un tensor esférico (tres
autovalores iguales) será un punto.
TS
TS max = 2,5
TII = TIII = −1
4 0 0 
Tij = 0 − 1 0 
0 0 − 1
TN
TI = T N max = 4
Figura A.8: Representación gráfica de un tensor simétrico con dos autovalores iguales.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
148
El cuarto ejemplo se trata de un tensor no simétrico que tiene un único autovalor real e
igual a T1 = −0,964 , y dos imaginarios, ver Figura A.9, y además se trata de un tensor no
definido positivo.
TS
 6 8 4
Tij = − 2 2 1 
 1 7 2
TS max
T N max = 9,894; TS = 6,0
T N min = −2,02; TS = 4,17
TN
TI = −0,964
TN min = −2,02; TS = −4,17
T N max = 9,894; TS = −6,0
TSsym
TSsym max
TIsym
= −2,02
II
Tijsym
TIsym
= 2,126
I
 6 3 2,5
=  3 2 4 
 2,5 4 2 
TN
TIsym = 9,894
Figura A.9: Representación gráfica de un tensor no simétrico con un único autovalor real.
En los planos correspondientes a las direcciones principales de la parte simétrica del tensor
tenemos los siguientes valores para la componente tangencial del tensor:
Para el autovalor TIsym = 9,894 tenemos que:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
5 1,5   − 0,707427855
 0
r (nˆ )

TS = ± t anti = ±  − 5 0 − 3  − 0,514420622  = ±
 − 1,5 3 0   − 0,484682632
149
− 3,299127 
 4 ,991187  = ±6,0


 − 0.482120
(A.26)
= −2,02 tenemos que:
Para el autovalor TIsym
II
5 1,5   0 ,0575152387 
 0
r (nˆ )

TS = ± t anti = ±  − 5 0 − 3  − 0 ,72538138475 = ±
 − 1,5 3 0   0 ,685940116897 
 − 2 ,5979967 
 − 2 ,3453965 = ±4,1676


− 2 ,2624170
(A.27)
A.3.1 Representación Gráfica de un Tensor de Segundo
Orden Simétrico. Círculo de Mohr.
Como hemos visto, la proyección de un tensor de segundo orden según una dirección
r ˆ
resulta un vector, t (n) = T ⋅ nˆ , y a su vez este vector puede ser descompuesto en una
componente normal y tangencial, cuyos módulos representamos respectivamente por TS y
T N , ver Figura A.1. El objetivo en este apartado es: dadas las componentes de un tensor
encontrar todo los valores posibles del par ( T N × TS ), esta representación gráfica
denominamos de Círculo de Mohr, y tiene varias aplicaciones prácticas dentro del ámbito
de ingeniería.
Consideraremos un tensor de segundo orden simétrico y por conveniencia, trabajaremos en
el espacio principal (direcciones principales) y supongamos que las componentes normales
(autovalores) están ordenadas: TI > TII > TIII . Partiremos de la expresión obtenida en (A.7),
i.e.:
r ˆ r ˆ
r ˆ
TS2 + T N2 = t (n) ⋅ t (n) = t (n)
2
(A.28)
x 3′
x 3′
C
T III
TI
S
T II
TI
T II
n̂
ê′3
O
x ′2
ê′2
ê1′
r ˆ
t (n)
B
x ′2
T III
x1′
A
a)
x1′
b)
Figura A.10: Representación de las componentes (tensor simétrico) en el espacio principal.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
150
r
ˆ
Las componentes del vector proyección t (n) , para un plano arbitrario, fueron obtenidas en
la ecuación (A.1). Fijemos ahora que n̂ es el versor del plano respecto a los ejes principales.
r ˆ
Las componentes de t (n) = T ⋅ nˆ , en el espacio principal, (Figura A.10b), son:
ˆ
ˆ
ˆ
t 1(n) = TI n1
;
t (2n) = TII n 2
;
t 3(n) = TIIIn 3
r ˆ r ˆ
El producto escalar t (n) ⋅ t (n) en este espacio será:
r ˆ r ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
t (n) ⋅ t (n) = t i(n) eˆ ′i ⋅ t (jn) eˆ ′j = t i(n) t (jn) δ ij = t i(n) t i(n)
(A.29)
ˆ
(A.30)
ˆ
ˆ
ˆ
ˆ
ˆ
= t 1(n) t 1(n) + t (2n) t (2n) + t 3(n) t 3(n)
2 2
= TI2 n12 + TII2 n 22 + TIII
n3
Combinando las expresiones (A.28) y (A.30), obtenemos que:
2 2
TS2 + T N2 = TI2 n12 + TII2 n 22 + TIII
n3
(A.31)
La componente normal T N , en el espacio principal, viene expresada de la forma:
r ˆ
T N = t (n) ⋅ nˆ = Tij n j n i = TI n12 + TII n 22 + TIIIn 32
(A.32)
donde utilizamos la expresión (A.4).
Considerando la restricción: n i n i = 1 , n12 = 1 − n 22 − n 32 , y reemplazándola en la relación
anterior (A.32) hallamos el valor de n 22 :
T N = TI (1 − n 22 − n 32 ) + TII n 22 + TIIIn 32
⇒
n 22 =
T N − T III n 32 + TI n 32 − TI
( TII − TI )
(A.33)
Reemplazando también ( n12 = 1 − n 22 − n 32 ) en la ecuación (A.31) obtenemos:
TS2 + T N2
2 2
= TI2 n12 + TII2 n 22 + TIII
n3
(A.34)
2 2
= TI2 (1 − n 22 − n 32 ) + TII2 n 22 + TIII
n3
Sustituyendo n 22 obtenido en (A.33) en la ecuación anterior resulta:
TS2 + T N2 = [( TIII − TI )( TIII − TII )] n 32 + TII T N + TI T N − TII TIII
(A.35)
Despejando n 32 ;
n 32
( T N − TI )( T N − TII ) + TS2
=
( TIII − TI )( TIII − TII )
(A.36)
Análogamente, podemos obtener n12 y n 22 , resultando:
n12 =
( T N − TII )( T N − TIII ) + TS2
≥0
( TI − TII )( TI − TIII )
(a)
n 22 =
( T N − TIII )( T N − TI ) + TS2
≥0
( TII − TIII )( TII − TI )
(b)
( T N − TI )( T N − TII ) + TS2
≥0
=
( TIII − TI )( TIII − TII )
(c)
n 32
(A.37)
Considerando que TI > TII > TIII podemos verificar que las ecuaciones (A.37) (a) y (c)
tienen denominadores positivos, como consecuencia sus numeradores deberán ser
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
151
positivos, pues el miembro de la izquierda es positivo ( n i2 ≥ 0 ). Sin embargo, la ecuación
(A.37) (b) tiene denominador negativo, por lo que su numerador tendrá que ser negativo,
es decir:
[( T
=
]

− TII )( T N − TIII ) + TS2 ≥ 0
≥ 0
[( TI − TII )( TI − TIII )] > 0

( T N − TII )( T N − TIII ) + TS2 ≥ 0

2

( T N − TIII )( T N − TI ) + TS ≤ 0

n 22 =
≥ 0  ⇒ ( T N − TIII )( T N − TI ) + TS2 ≤ 0
[( TII − TIII )( TII − TI )] < 0


2
( T N − TI )( T N − TII ) + TS ≥ 0
2

T
T
T
T
T
(
−
)(
−
)
+
≥
0
I
II
N
N
S
n 32 =
≥0 
[( TIII − TI )( TIII − TII )] > 0


n12
N
[
]
[
]
(A.38)
Expandiendo las desigualdades anteriores (A.38) y factorizando, resultan:
TS2 + [T N − 12 ( TII + TIII )] ≥ [12 ( TII − TIII )]
2
2
TS2 + [T N − 12 ( TI + TIII )] ≤ [12 ( TI − TIII )]
2
2
(A.39)
TS2 + [T N − 12 ( TI + TII )] ≥ [12 ( TI − TII )]
2
2
Las ecuaciones anteriores son ecuaciones de círculos. El primer círculo, de centro
1
( TII + TIII ) y radio 12 ( TII − TIII ) , nos indica que los puntos factibles para el par ( T N ; TS )
2
estarán en el exterior del círculo C1
, incluyendo la circunferencia, ver Figura A.11. El
1
segundo círculo, de centro 2 ( TI + TIII ) y radio 12 ( TI − TIII ) , nos indica que los puntos
factibles estarán en el interior de la circunferencia C 2
, incluyendo la circunferencia.
La tercera ecuación nos indica que los puntos factibles serán exteriores a la circunferencia
C3
, cuya circunferencia tiene radio 12 ( TI − TII ) y centro 12 ( TI + TII ) . Teniendo en
cuenta las tres ecuaciones, la zona factible será la zona señalada en gris de la Figura A.11,
incluyendo las circunferencias C1 , C 2 , C 3 .
zona factible
TS
TII
TIII
C3
TI
TN
C1
C2
Figura A.11: Círculo de Mohr – zona factible.
En el círculo de Mohr podemos identificar los valores máximos de TS max obtenidos en el
subapartado anterior, de forma mas sencilla, ver Figura A.12.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
152
TIII
TIII
Punto N
TIII
Punto M
TII
TII
TII
TI
Punto Q
TI
Punto N ′
TI
Punto M ′
Punto Q′
TS
M
TS max
N
Q
TIII
TII
Q′
TI = T N max
TN
N′
M′
Figura A.12: Círculo de Mohr.
A.3.1.1
Obtención Gráfica del Vector Proyección en el Círculo de Mohr
A continuación explicaremos como encontrar la dirección de un plano arbitrario en el
Círculo de Mohr. Esto es útil porque una vez encontrada la dirección de la normal del
plano en el círculo de Mohr, la tensión normal ( T N ) y tangencial ( TS ) podrán obtenerse
r
ˆ
gráficamente, ya que asociado a esta dirección sólo habrá un vector proyección t (n) .
La normal debe cumplir la siguiente condición:
nˆ i nˆ i = 1
nˆ 12 + nˆ 22 + nˆ 32 = 1
2
 nˆ
 nˆ 1 
  +  2
 1
 1 
2
 nˆ

 +  3

 1
2

 =1


(A.40)
que es la ecuación de una esfera de radio 1 centrada en el origen. Es decir, la superficie de
la esfera de radio uno es el lugar geométrico posible de n̂ i .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
153
TIII
C
K
n̂
γ
ê1′
H
Q
ê′3
α
G
F
TIII
n̂
γ
β
O
ê′2
α
TII
TI
B
O
β
A
TII
E
D
TI
b)
a)
Figura A.13: Lugar geométrico del vector n̂ .
Consideremos los cosenos directores del vector n̂ : nˆ 1 = cos(α ) , nˆ 2 = cos(β) , nˆ 3 = cos(γ ) ,
Figura A.13(a). En un octante de la esfera, Figura A.13(b), esta normal está representada
→
por el vector OQ . El objetivo ahora es identificar el punto Q en el círculo de Mohr. Una
vez identificado, el vector proyección correspondiente será el vector con origen en el punto
o de la Figura A.14 y final en el punto q .
Los vectores situados en el arco FD forman un ángulo α con el eje TI ; los vectores
situados en el arco EG forman un ángulo β con el eje TII y los vectores situados en el
arco KH forman un ángulo γ con el eje TIII . Por tanto, la intersección de estos tres arcos
será el punto Q , es decir, la dirección de la normal n̂ . Si además podemos identificar los
tres arcos en el círculo de Mohr, el punto Q queda definido.
Identificación de Arco FD en el Círculo de Mohr
Los vectores proyecciones correspondientes a las normales situadas en la
semicircunferencia CA de la Figura A.13(b) estarán situados en el círculo de Mohr en la
semicircunferencia ca ( TIII − TI ), de la Figura A.14. Un punto arbitrario del cuarto de
circunferencia ( CA ), por ejemplo el punto F de la Figura A.13(b), será identificado en el
círculo de Mohr cuando una recta con origen en σ III y con ángulo α , como indica la
Figura A.14, intercepte la semicircunferencia ca mostrando el punto f , que es el
correspondiente punto F de la esfera. Por otro lado, el arco FD es paralelo al cuarto de
circunferencia, BC que se corresponde con la semicircunferencia bc ( TII − TIII ) en el
círculo de Mohr. Por último, el arco FD estará representado en el círculo de Mohr por una
semicircunferencia concéntrica a la semicircunferencia TII − TIII y que pase por el punto
f , ver Figura A.14. El punto q , por tanto, se encontrará en el arco fd .
Identificación del Arco KH en el Círculo de Mohr
El punto K , en el círculo de Mohr, se corresponde con la intersección de la
semicircunferencia ca ( TI − TIII ) y de la recta con origen en TI y ángulo de γ , ver Figura
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
154
A.14. Una vez identificado el punto K en el círculo de Mohr, representado por k , el arco
KH deberá ser concéntrico a la semicircunferencia ab ( TI − TII ) y pasando por el punto
k , obtenemos así el punto h que es el equivalente punto H de la esfera.
La intersección de los dos arcos, fd y kh , nos proporciona el punto q .
Aunque no es necesario, identificaremos el arco EG por razones didácticas.
Identificación del Arco EG en el Círculo de Mohr
El punto E de la esfera estará representado en el círculo de Mohr por la intersección de la
semicircunferencia ab ( TI − TII ) y la recta con origen en TI y que forma un ángulo β con
TII . Una vez identificado el punto e , trazamos el arco eg que será concéntrico con la
semicircunferencia ac ( TI − TIII ), ver Figura A.14. El arco eg tendrá que contener el
punto q , como se indica en la Figura A.14.
r ˆ
t (n)
r
TS
TS
r
TN
ŝ
f
q
TS
g
r ˆ
t (n)
TIII , c
n̂
h
d
α
o
k
e
β
TN
TII , b
γ
TI , a
TN
Figura A.14: Vector proyección arbitrario en el círculo de Mohr.
A.4 Elipsoide del Tensor
Consideremos un tensor simétrico de segundo orden T , y sus autovalores representados
por T1 , T2 y T3 . En el espacio principal de T se cumple que:
r ˆ
T ⋅ nˆ = t (n)
componente

s →
t 1(nˆ ) = T1nˆ 1
 ˆ
(n )
t 2 = T2 nˆ 2
 (nˆ )
t = T3nˆ 3
 3
⇒
ˆ

t 1(n)
nˆ 1 =
T1

ˆ

t (2n)
ˆ
n
=
 2
T2


(nˆ )
nˆ 3 = t 3

T3
(A.41)
El objetivo ahora es: obtener la superficie, en el espacio principal, que describe el vector
r ˆ
t (n) para todos los valores posibles de n̂ .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
155
Teniendo en cuenta que un versor ( n̂ ) cumple que nˆ 12 + nˆ 22 + nˆ 32 = 1 (módulo unitario), y
reemplazando los valores de n̂ i dados por (A.41), obtenemos que:
T12
ˆ 2
ˆ 2
ˆ 2
t 1(n)
+
t (2n)
T22
+
t 3(n)
T32
(A.42)
=1
Que representa una superficie (elipsoide) en el espacio principal de T . Cuando dos
autovalores son iguales tenemos el caso de un elipsoide de revolución. Cuando los tres
autovalores son iguales la superficie será una esfera. Por eso, los tensores que presentan
esta característica se denominan Tensores Esféricos, y cualquier dirección será una dirección
principal.
ˆ
x 2′ , t (2n)
ˆ
x1′ , t 1(n)
T2
T1
n̂
r ˆ
t (n)
T3
ˆ
x3′ , t (3n)
Figura A.15: Elipsoide del tensor.
A.5 Representación Gráfica de la Parte Esférica
y Desviadora
A.5.1
Tensiones Octaédricas
Consideremos el espacio principal del tensor T y un plano octaédrico ABC , que por
definición, es un plano cuya normal n̂ forma el mismo ángulo ( α ) con los ejes principales,
ver Figura A.16. La normal a este plano obtenemos fácilmente partiendo de la condición
que nˆ i nˆ i = nˆ 12 + nˆ 22 + nˆ 32 = 1 , ya que nˆ 1 = nˆ 2 = nˆ 3 , resulta que 3nˆ 12 = 1 , luego, la normal al
r ˆ
plano resulta ser nˆ i = [ 13 13 13 ] . A este plano está asociado un vector octaédrico t (n) .
r
El vector normal a este plano se la denomina Vector Normal Octaédrica ( T Noct ) y el vector
r
tangencial denominamos de Vector Tangencial Octaédrica ( TSoct ), ver Figura A.16.
En el espacio de las direcciones principales, el vector tensión es:
r ˆ
T
T
T
t (n ) = T ⋅ nˆ = 1 eˆ 1′ + 2 eˆ ′2 + 3 eˆ ′3
3
3
3
(A.43)
A partir del vector octaédrico, asociado al plano ABC , dado por la relación (A.45),
r
obtenemos el módulo del vector T Noct , denominada de componente normal octaédrica, a través
de la forma:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
156
r ˆ
= t (n) ⋅ nˆ
T Noct
T
  eˆ ′ eˆ ′
T
eˆ ′ 
T
=  1 eˆ 1′ + 2 eˆ ′2 + 3 eˆ ′3  ⋅  1 + 2 + 3 
3
3   3
3
3
 3
I
1
1
= ( T1 + T2 + T3 ) = Tii = σ = Tm
3
3
3
r
T Noct - vector normal octaédrica
r
TSoct - vector tangencial octaédrica
T3
r (nˆ )
t
C
r
TSoct
T2
O
n̂
α
α
(A.44)
r
T Noct
OA = OB = OC
T1
α
B
T2
1
ˆn i = 1 1
3
1
trisectriz
T3
A
T1
Figura A.16: Vector tensión en el plano octaédrico.
En el espacio de las direcciones principales se cumple que:
r ˆ
T
T
T
t (n ) = T ⋅ nˆ = 1 eˆ 1′ + 2 eˆ ′2 + 3 eˆ ′3
3
3
3
(A.45)
A partir del vector octaédrico, asociado al plano ABC , dado por la relación (A.45),
r
obtenemos el módulo del vector T Noct , denominado de componente normal octaédrica, a través
de la forma:
T Noct
r ˆ
= t (n) ⋅ nˆ
T
eˆ ′ 
T
  eˆ ′ eˆ ′
T
=  1 eˆ 1′ + 2 eˆ ′2 + 3 eˆ ′3  ⋅  1 + 2 + 3 
3
3   3
3
3
 3
Iσ
1
1
= ( T1 + T2 + T3 ) = Tii =
= Tm
3
3
3
(A.46)
El módulo del vector tangencial octaédrico, definido como Componente Tangencial Octaédrica
( TSoct ), será:
TSoct
2
r ˆ r ˆ
2
= t (n) ⋅ t (n) − T Noct
1
1
2
= T12 + T22 + T32 − [T1 + T2 + T3 ]
3
9
1
= 2 I T2 − 6 II T
9
[
(
]
)
(A.47)
La ecuación anterior también puede ser expresada como:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
TSoct
=
1
3
(T1 − T2 )2 + (T2 − T3 )2 + (T3 − T1 )2
=
1
3
(T11 − T22 )2 + (T22 − T33 )2 + (T33 − T11 )2 + 6 (T122 + T232 + T132 )
=
157
(A.48)
−2
II dev
3 T
o en función de los valores principales del tensor desviador T dev :
TSoct =
(T ) + (T ) + (T )
dev 2
1
dev 2
2
dev 2
3
(A.49)
3
Podemos observar que las componentes octaédricas normal y tangencial son las mismas
para los 8 planos octaédricos, ver Figura A.17. Pudiendo entonces, resumir las distintas
formas de expresar las componentes normal y tangencial octaédricas:
T Noct =
TSoct
IT
= Tm
3
Componente normal
octaédrica
(A.50)
Componente
tangencial
octaédrica
(A.51)
(T ) + (T ) + (T )
dev 2
1
1
−2
2 I T2 − 6 II T =
=
II dev =
3
3 T
dev 2
2
dev 2
3
3
T3
r
T Noct
r
T Noct
r
TSoct
r
T Noct
r
TSoct
T2
r
TSoct
r
TSoct
r
T Noct
T1
Figura A.17: Vectores sobre los planos octaédricos.
Consideremos una vez más el espacio definido por las direcciones principales, representado
por la base ortonormal ( eˆ 1′ , eˆ ′2 , eˆ ′3 ), Figura A.18. En este espacio plotamos las coordenadas
de los valores principales de T , el cual denotamos por el punto P .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
158
Eje esférico
Π′
T1
P ( T1 , T 2 , T 3 )
T1 = T2 = T3
q
A(Tm , Tm , Tm )
ê1′
Π
p
α
O
ê′2
1
ˆn i = 1 1
3
1
α
n̂
α
Plano desviador
ê′3
(Plano octaédrico)
T3
T2
Plano desviador Π
(Plano de Nadai)
Figura A.18: Espacio principal.
En este espacio, considere el segmento de recta OA que pasa por el origen, según la
dirección de n̂ . Cualquier punto de esta línea está caracterizado por el estado tensorial
T1 = T2 = T3 , denominándose, por tanto, eje esférico.
Cualquier plano perpendicular al eje esférico será un plano desviador (o plano octaédrico). Un
plano desviador particular es el plano que pasa por el origen, denominado plano- Π , en este
caso la ecuación del plano es T1 + T2 + T3 = 0 , ver Figura A.18. Cualquier punto en el
plano Π representa un estado desviatórico puro.
Considerando un estado tensorial arbitrario en un punto P representado por los valores
principales ( T1 , T2 , T3 ), como se indica en la Figura A.18, podemos establecer algunas
características interesantes. Este punto ( P ) pertenecerá a un plano desviador Π ′ ,
→
→
→
definiéndose así los siguientes vectores: OP , OA y AP .
→
El vector OP puede ser expresado en función de los valores principales de la forma:
→
(A.52)
OP = T1eˆ 1′ + T2 eˆ ′2 + T3 eˆ ′3
→
Según la Figura A.18, el módulo de OA es:
→
→
OA = p = OP⋅ nˆ
 eˆ ′ eˆ ′
eˆ ′ 
= (T1eˆ 1′ + T2 eˆ ′2 + T3 eˆ ′3 ) ⋅  1 + 2 + 3 
3
3
 3
T1 + T2 + T3
=
3
3 Tm
=
= 3 Tm = 3 TSoct
3
p = 3 Tm = 3 TSoct
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
(A.53)
(A.54)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
159
→
Por tanto, podemos escribir el vector OA como:
→
OA
→
= OA nˆ
 eˆ ′ eˆ ′
eˆ ′ 
= 3 Tm  1 + 2 + 3 
3
3
 3
ˆ
ˆ
ˆ
′
′
′
T
T
T
= m e1 + m e 2 + m e 3
(A.55)
→
El punto A tiene las coordenadas ( Tm , Tm , Tm ). Una vez definidos los vectores OP y
→
→
OA , utilizamos la suma de vectores para obtener el vector AP , ver Figura A.18:
→
→
→
(A.56)
AP = OP − OA
Considerando las expresiones (A.52) y (A.55), la relación anterior resulta:
AP = T1 eˆ 1′ + T2 eˆ ′2 + T3 eˆ ′3 − (Tm eˆ 1′ + Tm eˆ ′2 + Tm eˆ ′3 )
= ( T1 − Tm )eˆ 1′ + ( T2 − Tm )eˆ ′2 + ( T3 − Tm )eˆ ′3
→
(A.57)
= T1dev eˆ 1′ + T2dev eˆ ′2 + T3dev eˆ ′3
Empleando la definición Tijdev = Tij − Tm δ ij , la expresión anterior puede escribirse de la
forma:
→
(A.58)
AP = T1dev eˆ 1′ + T2dev eˆ ′2 + T3dev eˆ ′3
→
Las componentes del vector AP representan las componentes del tensor desviador Tijdev .
→
El módulo de AP será:
(T ) + (T ) + (T )
→
dev 2
1
q = AP =
dev 2
2
dev 2
3
= I T2 dev − 2 II T dev = − 2 II T dev
(A.59)
Teniendo en cuenta la expresión de TSoct dada por (A.49), aún podemos decir que:
q = − 2 II T dev = 3 TSoct
(A.60)
→
También podríamos haber obtenido el módulo de AP utilizando el teorema de Pitágoras:
→
AP
2
→
→
2
= OP − OA
→
⇒ AP =
2
= T12 + T22 + T32 −
1
(T1 + T2 + T3 )2
3
(
)
2 2
T1 + T22 + T32 − T1 T2 − T2 T3 − T3 T1 = q
3
(A.61)
(A.62)
donde q indica lo alejado que el estado tensorial del punto P está del estado esférico, ver
Figura A.18.
Podemos obtener la proyección del espacio principal sobre el plano Π , ver Figura A.19,
→
para determinar la orientación de AP .
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
160
Π′ , Π
T1′
T1
Q′
P
q
θ
cos α =
ê1′
ê1′′ q cos θ
α
1
3
n̂
O
eˆ ′2 , eˆ ′3
120 º
T2 , T3
T2′
T3′
Figura A.19: Proyección de las tensiones principales sobre el plano de Nadai.
Para obtener las componentes del versor eˆ 1′′ = a1eˆ 1′ + a 2 eˆ ′2 + a 3 eˆ ′3 , Figura A.19,
consideremos el sistema principal como muestra en la Figura A.20, donde se cumple que
cos β = sin α =
2
3
= a1 , a 2 = a 3 , y además teniendo en cuenta que el eje esférico es
ortogonal al plano desviador obtenemos que:
1 ˆ
(e1′ + eˆ ′2 + eˆ ′3 ) = 0
eˆ 1′′ ⋅ nˆ = (a1 eˆ 1′ + a 2 eˆ ′2 + a 3 eˆ ′3 ) ⋅
3
1
(a1 + a 2 + a3 ) = 0
⇒
3
⇒ a 2 + a 3 = −a1 = −
2
3
=−
(A.63)
2
6
Y además:
1
2
1
a 2 = a 3 = − a1 = −
=−
2
2 3
6
(A.64)
1
eˆ 1′′ =
( 2eˆ 1′ − eˆ ′2 − eˆ ′3 )
6
(A.65)
Resultando así:
Obtenemos así la proyección del vector OP según la dirección de ê1′′ como:
OP ⋅ eˆ 1′′ = ( T1dev eˆ 1′ − T2dev eˆ ′2 − T3dev eˆ ′3 ) ⋅
=
1
6
(2 T1dev
−
T2dev
−
T3dev )
1
6
( 2eˆ 1′ − eˆ ′2 − eˆ ′3 )
(A.66)
= q cos θ
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
APÉNDICE A: REPRESENTACIÓN GRÁFICA DE UN TENSOR
161
T3
T1
n̂
2
ê1′
ê1′′
β α
ê′3
3
T2
ê′2
Figura A.20: Espacio principal.
Considerando que T1dev + T2dev + T3dev = 0 ⇒ − T1dev = T2dev + T3dev y reemplazando en la
ecuación anterior resulta:
q cos θ = OP ⋅ eˆ 1′′ =
1
6
(2 T1dev + T1dev ) =
3
6
T1dev =
3 dev
T1
2
(A.67)
Considerando que q = − 2 II T dev , tenemos:
q cos θ =
3 dev
T1
2
− 2 II T dev cos θ =
3 dev
T1
2
cos θ =
3
2
T1dev
− 2 II T dev
(A.68)
⇒
T1dev =
2
3
− II T dev cos θ
Análogamente podemos obtener T2dev , T3dev . Pudiendo así representar las tensiones
principales, Tij = Tm δ ij + Tijdev , explícitamente como:
 T1
0

 0
0
T2
0
0   Tm
0  =  0
T3   0
 Tm
=  0
 0
0
Tm
0
0
Tm
0
0   T1dev

0  +  0
Tm   0
0
T2dev
0
0 
2
0  +
− II T dev
3
Tm 
0 

0 
T3dev 
cos θ
0

cos(θ −
 0
 0
0



2π
)
0
3

cos(θ + 23π )
0
(A.69)
siendo 0 ≤ θ ≤ π / 3 . El estado de tensión puede expresarse según el sistema ( p, q, θ ), que
son las denominadas coordenadas de Haigh-Westergaard:
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves
MECÁNICA DEL MEDIO CONTINUO: CONCEPTOS BÁSICOS
162
 T1
0

 0
0
T2
0
cos θ

0
0
0
 p 0 0
1 
2 



2π
q 0
0=
0 p 0 +
cos(θ − 3 )
0


3
3
2π 
 0
 0 0 p 
T3 
0
cos(
)
θ
+
3 
 4444424444444
1442443 144
3
Parte
Esférica
(A.70)
Parte
Desviadora
Reemplazando el cos θ dado por la expresión (A.68) en la siguiente relación trigonométrica
cos 3θ = 4 cos 3 θ − 3 cos θ , hallamos que:

 3
cos 3θ = 4
 2

cos 3θ =
(
3



 3
 − 3

 2


T1dev
− II T dev
3 3
2 − II T dev
)
3


(
)
3
T1dev
T1dev
− II T dev





(A.71)
+ T1dev II T dev 

considerando II T dev = ( T1dev T2dev + T2dev T3dev + T1dev T3dev )

 3
cos 3θ = 4
 2

cos 3θ =
(
3
T1dev
− II T dev
3 3
2 − II T dev
)
3



 3
 − 3
 2



(
 dev
 T1






T1dev
− II T dev
) + (T ) (1T 42
+ T )+ T T T
4 43
4 14
4244
3
3
cos 3θ =
dev 2
1
dev
2
dev
3
− T1dev
3 3 III T dev
(
2 − II T dev
)
3
dev
1
dev
2
J3
dev
3



(A.72)
(A.73)
Al ser II T dev , III T dev invariantes, cos 3θ también lo es.
Mecánica del Medio Continuo: Conceptos Básicos (3ª Edición)
Por: Eduardo W.V. Chaves