Document

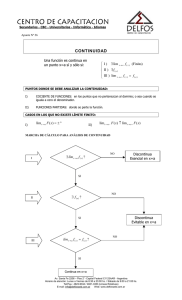
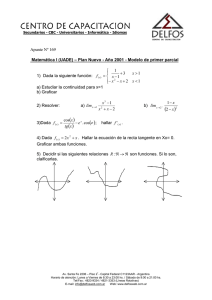
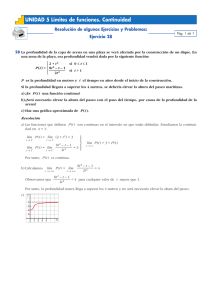
C
CÁ
ÁL
LC
CU
UL
LO
O IIN
NT
TE
EG
GR
RA
AL
L
IIN
NT
TE
EG
GR
RA
AL
LD
DE
EF
FIIN
NIID
DA
A
Hemos visto que, por el cálculo diferencial o proceso de derivación, es posible definir con precisión la
recta tangente a una curva en un punto. Veremos aquí que es posible definir con precisión el área de
una región plana utilizando el concepto de Integral Definida. Si bien estos dos problemas, la recta
tangente a una curva en un punto y el área de una figura plana, se resuelven por procesos independientes, ambos están vinculados. Esta vinculación se manifiesta en el Teorema Fundamental del
Cálculo Integral, que relaciona el concepto de Derivada con el de Integral Definida, conceptos que
forman el núcleo del Cálculo Diferencial e Integral.
En geometría elemental se deducen fórmulas para calcular el área de ciertas figuras (triángulos, rectángulos, círculos, etc.), pero si reflexionamos un poco, veremos que rara vez se da un definición
aceptable del área.
A veces, se define el área de una región como el número de cuadrados de lado unidad que cabe en
la región. Esto es claro si la región es un rectángulo:
En este rectángulo caben 8 cuadraditos cuyo
lado es la unidad, y todos sabemos que el área
del mismo es A = base x altura = 4x2 = 8
Pero si consideramos que la región es el círculo de radio r = 2 :
Sabemos que su área es
A = π . r 2 = π.22 =4π
Pero no queda claro en absoluto el significado
de que 4π cuadrados caben en esta región
En el caso general, si consideramos una región R como la de la siguiente figura:
Vemos que no sólo es complicado calcular
su área, sino que además es dificultoso dar
una definición de área
Análisis Matemático I - Página 1
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
Para “definir” en forma precisa el área, tratemos en principio el problema de “calcular” el área de la
región plana R, limitada por una función continua y positiva ƒ, el eje x y las verticales x = a y
x = b:
Dividamos el intervalo cerrado [a , b] en n subintervalos de igual longitud. Si la longitud del intervalo
[a , b] es igual a b - a entonces la longitud de cada subintervalo será ∆x =
b-a
> 0 . De manera
n
que los extremos de estos subintervalos son:
x0 =a, x1 = a+ ∆x , x 2 = a+ 2∆x , x 3 = a+ 3∆x , x 4=a+ 4∆x, . . ., xn = b
A los subintervalos [ x0 , x1 ] , [ x1 , x2 ] , ... , [ xn-1 , xn ] , con x0 = a y xn = b los podemos simbolizar
más brevemente con [ x i - 1 , x i ] donde 1 ≤ i ≤ n .
Ahora tomemos en cada subintervalo [ x
i -1
,xi ] , 1 ≤ i ≤ n , un punto muestra xi* cualquiera y
formemos el rectángulo cuya base es el intervalito y cuya altura es f ( xi* ) , o sea la imagen de xi* :
Como el área de cada rectángulo es el producto de ∆x ( base ) y f ( xi* ) ( altura ) , se ve que la suma
de las áreas de todos los rectángulos nos da una medida aproximada del área de la región R. Esta
suma se puede expresar usando la notación sigma:
n
∑ f ( xi* ) . ∆x =
i =1
f ( x1* ) ∆x + f ( x2* ) ∆x + f ( x3* ) ∆x + f ( x4* ) ∆x + ... + f ( xn* ) ∆x
Para abreviar simbolicemos la suma (1) con Rn =
n
∑ f ( xi* ) . ∆x .
i =1
Análisis Matemático I - Página 2
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
(1)
Por ejemplo, si la cantidad de subintervalos es n = 4, (1) queda
4
R4 = ∑ f ( xi* ) . ∆x = f ( x1* ) . ∆x + f ( x2* ) . ∆x + f ( x3* ) . ∆x + f ( x4* ) . ∆x y ésta simboliza la suma de las
i =1
áreas de los 4 rectángulos que quedan definidos.
Ahora observemos las siguientes figuras en las que se representan los rectángulos de aproximación
y en cada una se toma un valor de n distinto:
Usando el programa GeoGebra podemos visualizar en forma dinámica este tipo de gráficos y
a la vez conocer el valor de la suma (1) para distintos valores de n . Si consideramos la función
f ( x) = x 2 en el intervalo cerrado [0 , 1] se puede observar que, a medida que incrementamos la
cantidad de intervalitos, las sumas se van aproximando al valor 1/3.
Es decir, intuimos que a medida que tomamos n “ cada vez más grande ”, las aproximaciones correspondientes del área de R, son cada vez mejores. Dicho de otra manera, intuimos que el límite de
las sumas, cuando n tiende a ∞ , será el valor exacto del área de la región R:
Definición: El área de la región R delimitada por la gráfica de una función continua y positiva
eje x, x = a y x = b, es el límite de la suma de las áreas de los rectángulos de aproximación:
Área de R = lím Rn = lím
n→∞
Como
ƒ es continua
n→∞
ƒ , el
[ f ( x1* ) ∆x + f ( x2* ) ∆x + f ( x3* ) ∆x + ... + f ( xn* ) ∆x]
y ∆x es constante, este límite siempre existe.
Ejemplo: Usando esta definición, calculemos el área de la región encerrada por la gráfica de
f ( x) = x 2 , el eje x, x = 0 y x = 1.
Sabemos que ƒ es continua y positiva en el intervalo cerrado [0 , 1].
Análisis Matemático I - Página 3
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
Dividamos al intervalo cerrado [0 , 1] en n partes de igual longitud ∆x =
b-a
1- 0
1
=
= . O sea
n
n
n
1
y quedan determinados los subintervalos
n
n
1
1 2
2
3
3
4
n -1
] , [ ,
],[
,
], [
,
]... , [
,
= 1 ]. Como un punto muestra puede ser
[0,
n
n
n n
n
n
n
n
n
cualquier valor del subintervalo correspondiente, podemos tomar como puntos muestras xi* a los
que el ancho de los rectángulos es
extremos derechos de cada subintervalo:
x1*
= 1
n
, x 2* = 2 , x3* = 3 , x 4* = 4 , . . ., x n* = n .
n
n
n
n
Como la altura de cada rectángulo es la imagen por ƒ de estos puntos, las alturas son:
(1n )2 , (n2 )2 , (n3 )2 , (n4 )2 , ..., (nn )2
Entonces Rn =
n
∑ f ( xi* ) . ∆x = ( 1n ) 2 . 1n + ( n2 ) 2 . 1n + ( n3 ) 2 . 1n + . . . + ( nn ) 2 . 1n
i =1
= 1n . 1 ( 12 + 2 2 + 3 2 + . . . + n 2 )
n2
= 1 ( 12 + 2 2 + 3 2 + . . . + n 2 )
n3
Utilizando la fórmula para la suma de los cuadrados de los primeros naturales:
n ( n + 1)(2n + 1)
♣ 12 + 2 2 + 3 2 + . . . + n 2 =
6
La suma queda Rn =
1 n (n + 1)(2n + 1) (n + 1)(2n + 1)
=
.
6
n3
6n 2
Ahora hagamos:
∞
(n + 1)( 2n + 1) ∞
lím Rn = lím
=
n→∞
n→∞
6n 2
1 ( n + 1) ( 2n + 1)
1 1 
1
1 1
.
= lím 1 + . 2 +  = .1.2 =
n→∞ 6
n→∞ 6 
n
n
n
n 6
3
= lím
Y confirmamos que nuestra intuición no falló, el área descripta es 1/3.
Observación importante: Recuérdese que la altura de un rectángulo siempre es positiva, entonces
f ( xi* ) sea la altura de un rectángulo de aproximación, ƒ debe ser positiva en el intervalo
[a , b]. En otras palabras: sólo si f(x) ≥ 0, ∀x ∈ [a, b ] , el límite lím Rn da el valor exacto del valor
para que
n→∞
del área de la región limitada por la gráfica de la función continua ƒ , el eje x y las verticales
x = a y x = b.
.
Ejercicio: Calcular el área de la región encerrada por la gráfica de f ( x) = x 2 , el eje x, x = 0 y x = 1,
tomando como punto muestra en cada subintervalo el extremo izquierdo del subintervalo. ¿Cuál es el
resultado?. ¿ Porqué ?.
Análisis Matemático I - Página 4
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
El límite
lím Rn = lím
n→∞
n→∞
[ f ( x1* ) ∆x + f ( x2* ) ∆x + f ( x3* ) ∆x + ... + f ( xn* ) ∆x]
que utilizamos para cal-
cular área aparece en muchas situaciones, incluso cuando la función no es positiva. El mismo se
utiliza para calcular longitudes de curvas, volúmenes de sólidos ( como veremos más adelante), centros de masa, trabajo, etc. Es por ello que le damos una definición especial:
Definición: Si ƒ es una función continua en un intervalo cerrado [a , b] , dividimos el intervalo
b-a
. Hacemos que a=x0 ,x1 , x2 , ... , xn-1 , xn =b
n
sean los puntos extemos de estos subintervalos y elegimos x1* , x2* , x3* , …, xn* como los puntos
[a , b] en n subintervalos de igual ancho ∆x =
muestras en estos subintervalos, de modo que xi* se encuentre en el i-ésimo subintervalo
[ xi -1 , xi ]. Entonces la Integral Definida de ƒ, desde a hasta b , se define como
∫
b
f (x) dx = lím
n→∞
a
n
∑ f ( xi* ) . ∆x
i =1
y diremos que ƒ es integrable sobre el intervalo cerrado [a , b].
Observación 1 :
ƒ es continua, este límite siempre existe y da el mismo valor independien-
Como
temente de cómo se elijan los puntos muestra xi* .
Observación 2 : Se puede probar que el límite de la definición anterior existe también si la función
es acotada y tiene un número finito de discontinuidades en [a , b]. O sea que existe la Integral Defib
nida
∫ ƒ(x) dx para tales funciones. Si los puntos de discontinuidad son t , t
que
a < t0 < t1 < t2 < ... < tn-1 <tn < b la integral es igual a
b
∫
a
0
a
ƒ(x) dx =
t
∫
0
a
ƒ(x) dx +
t
1
t
∫
ƒ(x) dx +
0
t
∫t
, t2 , ... , tn-1 ,tn tales
b
∫t
ƒ(x) dx+ . . . + ƒ(x) dx
2
n
1
Observación 3 : La integral definida
1
∫
b
a
ƒ(x) dx , es un número real, positivo, negativo ó cero.
Observación 4 : Si comparamos la definición de Integral Definida con la definición de área dadas,
sólo en el caso en que
ƒ(x) ≥ 0 en
[a , b], las sumas Rn =
n
∑ f ( xi* ) . ∆x
son aproximaciones del va-
i =1
lor del área de la región limitada por la gráfica de la función continua ƒ , el eje x y las verticales
x = a y x = b, y la Integral Definida da el valor exacto de este área.
Nota: El símbolo
∫
se llama signo de integral y fue introducido por Leibniz. Es una S alargada y
fue elegida pues la integral es un límite de sumas. En el símbolo
∫
b
a
ƒ (x) dx, a ƒ (x) se lo llama in-
tegrando, a y b son los extremos inferior y superior de integración y x se denomina variable de
integración. El símbolo dx carece de significado aisladamente.
Observación 5 : La Integral Definida es un número que no depende de x. Por ello:
Análisis Matemático I - Página 5
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
∫
b
a
ƒ(x) dx
=
tremos a y b .
∫ ƒ(t) dt = ∫ ƒ(z) dz = ... Es decir, depende sólo del integrando ƒ(x) y de los exb
b
a
a
n
Observación 6 : La suma
∑ f ( xi* ) . ∆x
se denomina suma de Riemann, en honor al matemático
i =1
alemán Bernhard Riemann a quien se debe la definición dada de Integral Definida. Riemann fue el
primero en desvincular la misma de su interpretación geométrica como área. De manera que la Integral Definida es un concepto matemático dado por el límite lím
n→∞
n
∑ f ( xi* ) . ∆x y área es su significai =1
do o interpretación geométrica ( con las condiciones mencionadas en la observación 4 ).
Al introducir el concepto de Integral Definida, hemos supuesto que a < b . Ampliemos este concepto
con las siguientes definiciones:
Definición : Si a ∈
y ƒ es una función con a perteneciente a su dominio,
a
∫ f(x) dx =0 .
a
Definición : Si a < b y
ƒ es integrable sobre el
∫
[a , b] , se define
a
f(x) dx = -
b
0
plo:
∫x
1
2
∫
1
b
∫ f(x) dx . Por ejema
dx = - x dx = − 13 , donde hemos usado el resultado del ejercicio.
2
0
3
Ejemplo: Usemos la definición de Integral Definida para calcular
∫ (x
3
- 6x) dx
0
b-a
3-0 3
= de ma=
n
n
n
3
3
6
6
9
9 12
nera que quedan determinados los subintervalos [ 0 ,
] , [
,
],[
,
], [
,
]... ,
n
n
n
n
n
n
n
3n - 1 3n
,
= 3 ].
[
n
n
Podemos tomar como punto muestra xi* al extremo de la derecha de cada subintervalo, con lo cual:
Dividamos al intervalo cerrado [0 , 3] en n partes de igual longitud ∆x =
x0
=0
3i
, x1* = 3 , x2* = 6 , x3* = 9 , x 4* = 12 , . . ., xn* = 3n =3 . En general xi* =
n
n
n
n
n
n
Entonces
∫
3
(x 3 - 6x) dx = lím
n→∞
0
n
∑
n→∞
n→∞
i =1
n
= lím
f ( xi* ) . ∆x = lím
 3i 
∑  n 
i =1

3
−6
n
i =1
3i  3
.
n  n
 27i 3 18i 
∑
 3 −
 =
n→∞
n 
i =1  n
54 n 
 81 n
= lím  4 ∑ i 3 − 2 ∑ i 
n→∞
n i =1 
 n i =1
=
lím
3
n
3i 3
∑ f ( n ). n
n
 3 n 27i 3 3 n 18i 
lím  ∑ 3 − ∑ 
n→∞
n i =1 n 
 n i =1 n
Análisis Matemático I - Página 6
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
Ahora usemos las fórmulas:
n
♣
∑ i = 1+ 2 + 3 + . . . + n =
i =1
n
♣
∑
i =1
n ( n + 1)
2
Suma de los n primeros naturales
 n ( n + 1) 
i = 13 + 23 + 33 + . . . + n 3 = 
2 
Suma de los cubos de los n primeros
naturales
2
3


Entonces el límite queda:
 81  n(n + 1)  2 54 n( n + 1) 
 81  n( n + 1)  2
n(n + 1) 
−
−
=
(x 3 - 6x) dx = lím  4 
lím
27



2
2


n→∞
2  n → ∞  4  n
n 2 
0
 n  2  n
 81  1)  2
27
 1  81
= −6.75
= lím  1 +  − 27 1 +  = − 27 = −
n→∞
4
 n  4
 4  n 
∫
3
Esta integral no se puede interpretar como el valor del área de la región limitada por la gráfica de
f(x) = x 3 - 6x , el eje x, entre x = 0 y x = 3, porque esta función no es positiva en todo el intervalo
[0 , 3], sino que toma valores tanto positivos como negativos allí. En todo caso se puede decir que es
la diferencia ( área de A1 - área de A2 ), siendo A1 y A2 como se muestra en la figura:
Propiedades de la Integral Definida
Antes dijimos que tanto las funciones continuas en un [a , b] , como las funciones acotadas y continuas salvo en un número finito de puntos del [a , b] son integrables sobre este intervalo. Las siguientes propiedades se refieren a todas ellas.
P1) Sean a , b , c ∈
donde a < c < b . ƒ es integrable sobre [a , b] si, y sólo si,
sobre [a , c] y sobre [c , b] . En este caso
∫
b
a
ƒ(x) dx
=
∫
c
a
ƒ(x) dx
+
∫
b
c
ƒ(x) dx
Análisis Matemático I - Página 7
Printed with FinePrint 2000 - purchase at http://www.fineprint.com
ƒ
es integrable
P2) Si ƒ y g son funciones integrables sobre [a , b] , entonces
además:
∫
b
a
P3) Si
ƒ
es integrable sobre [a , b] y c ∈
y además:
∫
b
∫
b
En particular
1
Ejemplo:
- ƒ(x) dx = -
a
∫
5x2 dx = 5
0
∫
b
[ ƒ(x) dx ± g(x) ] dx =
1
∫
b
a
±
∫
b
a
cualquiera, entonces c
∫
b
c ƒ(x) dx = c
a
∫
ƒ(x) dx
ıg
es integrable sobre [a , b] y
g(x) dx
ƒ
es integrable sobre [a , b]
ƒ(x) dx
a
ƒ(x) dx.
a
x2 dx = 5.(1/3) = 5/3
0
P1, P2 y P3 valen también si a ≥ b.
P4) Si ƒ es integrable sobre [a , b] , entonces ƒ es integrable sobre cualquier [c , d] tal que
[c , d] ⊆ [a , b] .
P5) Si
ƒ
es integrable sobre [a , b] , entonces
 ∫ ƒ(x) dx 
b
P6) Sean
ƒ
a
b
a
ƒ(x) ≥ 0
(en particular: si
ƒ
en [a , b] ⇒
∫
b
ƒ(x) dx
a
ƒ
, b]. Además si
ƒ(x) dx
∫
b
a
es integrable sobre [a , b] y
m (b - a) ≤
b
a
y g integrables sobre [a , b] tales que
∫
P7) Si
∫
≤
 ƒ(x)  dx
ƒ(x)
∫
b
≤
a
≤ g(x) en [a , b] , entonces
g(x) dx
ƒ(x) dx ≥ 0 )
m ≤
ƒ(x)
≤ M
∀ x ∈ [a , b] , entonces
≤ M (b - a) . En particular: m y M pueden ser ínfimo y supremo de
es continua, m y M pueden ser el mínimo y el máximo de
ƒ
en [a
ƒ en [a , b] .
Otra definición de Integral Definida
De la definición de Integral Definida
∫
b
a
f (x) dx = lím
n→∞
n
∑ f ( xi* ) . ∆x
se desprende que en la suma
i =1
n
de Riemann
∑ f ( xi* ) . ∆x cuando
n tiende a ∞, ∆x tiende a 0.
i =1
Hay situaciones en que es más apropiado subdividir al intervalo cerrado [a , b] en n subintervalos de
distinta longitud. Si designamos con ∆x1, ∆x2, ∆x3, ∆x4 , . . . , ∆xn a las longitudes de estos subintervalos, debemos asegurarnos que, en el proceso del límite, estas longitudes tiendan a 0. Esto se consiAnálisis Matemático I - Página 8
Printed with FinePrint 2000 - purchase at http://www.fineprint.com