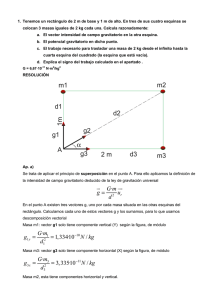
FÍSICA PAU+25 TEMA 6 Gravitación
Anuncio

FÍSICA. PRUEBA ACCESO A LA UNIVERSIDAD +25 TEMA 6. Gravitación La cosmología es la ciencia que explica el origen, estructura, evolución y las leyes que gobiernan el Universo. Las civilizaciones más antiguas utilizaron los objetos del Universo que podemos ver en nuestros cielos para establecer sistemas de referencia espaciales que les permitiera orientarse en sus desplazamientos y sistemas de referencia temporales para establecer calendarios. La civilización griega, en el siglo III a.C., había establecido la esfericidad de la Tierra, determinado su radio en unos 6000 km, la distancia relativa de la Tierra a la Luna y al Sol, etc. Sin embargo, el hecho más significativo fue la observación en el firmamento de puntos luminosos, las estrellas fijas y de puntos luminosos de trayectoria errante, los planetas. Platón (s. IV a.C.) defendió la teoría geocéntrica del Universo, según la cual la Tierra es esférica y ocupa el centro del Universo y los demás cuerpos giran alrededor de la Tierra. Aristóteles (s. IV a.C.) en su modelo geocéntrico establecía dos zonas. La zona sublunar formada por los cuatro elementos: tierra, agua, aire y fuego; y la zona celestial formada por éter y dividida en esferas concéntricas sobre las que se encuentran la Luna, Marte, etc. y al final la esfera de las estrellas. Aristarco de Samos (s. III a.C.) perteneciente a la escuela de Alejandría, realizó cálculos sobre los diámetros relativos de la Tierra y la Luna así como la distancia entre ellas. Propuso un sistema heliocéntrico con el Sol en el centro de la órbita de la Tierra que a su vez giraba alrededor de su eje una vez al día. Pero la autoridad de Aristóteles era tan grande que hasta el siglo XVI no se reconoció su validez. Eratóstenes de Cirene (s. III a.C.) ideó un sistema para demostrar la curvatura de la Tierra y estimar su radio. Claudio Ptolomeo (s. II) reforzó el modelo geocéntrico de Aristóteles para justificar el movimiento de los planetas mediante una combinación de movimientos circulares. Un planeta se mueve en una circunferencia (epiciclo) cuyo centro se mueve en otra circunferencia mayor (deferente) cuyo centro es la Tierra u otro punto simétrico respecto de la posición de la Tierra, lo que suponía la Tierra no era el centro del Universo. Esta descripción del Universo permaneció vigente hasta el siglo XVI. Nicolás Copérnico (1473-1543) llegó a la conclusión de que no existía solución al problema de los planetas si se centraba el Universo en la Tierra y propuso un modelo basado en los siguientes postulados: i) El centro del Universo lo ocupa el Sol (modelo heliocéntrico) alrededor del cual se mueven los planetas y la Tierra. ii) La Tierra realiza tres movimientos circulares: uno alrededor del Sol, otro sobre su propio eje y un movimiento de cabeceo de su eje de rotación. iii) La Luna se mueve alrededor de la Tierra. iv) Las estrellas están inmóviles y muy lejanas. Este modelo simplificaba la explicación del movimiento de los planetas y resolvía el movimiento retrógrado de algunos de ellos, pero no obstante tuvo sus detractores, entre ellos la iglesia católica y protestante. http://organizaciones.bornet.es/ala/La%20Astronom%C3%ADa%20en%20Grecia.htm Galileo Galilei (1564-1642) además de las importantes aportaciones en cinemática y dinámica, utilizó y perfeccionó el telescopio con el que realizó las siguientes observaciones: i) ii) iii) Júpiter tiene cuatro satélites (Io, Europa, Calisto y Ganímedes), luego no todo en el Universo gira alrededor de la Tierra. La superficie de la Luna presenta irregularidades e imperfecciones, por lo que la esfera lunar no era tan perfecta como afirmaba Aristóteles. Venus presenta fases como las de la Luna lo que hace pensar que gira alrededor del Sol y no de la Tierra. Tycho Brahe (1546-1601) fue un minucioso observador del movimiento de los planetas, también observó la explosión de una estrella y desmintió que los cometas fueran fenómenos atmosféricos. http://www.astrored.org/doc/articulo.php/francisco_rodriguez/brahe/1.html 1 http://newton.cnice.mec.es/2bach/campo_gravitatorio/index.htm Johannes Kepler (1571-1630) utilizó los precisos datos de Brahe sobre el movimiento de los planetas, en concreto Marte, y llegó a la conclusión de que las órbitas de éstos no podían ser circulares. Su teoría sobre el movimiento de los planetas se basa en tres leyes: Primera ley: Los planetas describen órbitas elípticas uno de cuyos focos lo ocupa el Sol. c exc a Segunda ley: En este movimiento, el radio entre el Sol y b a el planeta barre áreas iguales en tiempos iguales. c r2 r1 Tercera ley: Los cuadrados de los periodos de los planetas alrededor del Sol son proporcionales al cubo de sus distancias al sol. 2 TT 3 RT 2 TV 3 RV 2 TM 3 C RM donde C es un valor constante para cada sistema. http://thales.cica.es/rd/Recursos/rd98/Astronomia/03/astronomia03.html Perihelio Afelio A.1 Calcula la distancia media del Sol a Marte que tiene un periodo de revolución de 1,833 años. Busca los datos 1 correspondientes a la Tierra. (Sol: 1,5 UA ) ¿Cuál será el periodo de revolución de Júpiter que se encuentra a 5,2 UA del Sol? (Sol: 12 años) Las leyes de Kepler son aplicables a cualquier sistema de astros que giran alrededor de otro central. Describen sus movimientos pero no establecen las causas. A.2 Sabiendo la distancia del Sol a la Tierra y a Marte (del ejercicio anterior) estima la rapidez de traslación de ambos planetas. (Sol: 30000 m/s; 24500 m/s) http://www.sc.ehu.es/sbweb/fisica/celeste/kepler/kepler.htm Ley de Newton de la gravitación universal I. Newton (1642-1727) estudió el movimiento de la Luna alrededor de la Tierra. Supuso que la trayectoria de la Luna es una circunferencia y al ser este un movimiento variado debía de actuar sobre la Luna una fuerza dirigida hacia la Tierra cuyo valor debía de ser inverso al cuadrado de la distancia entre la Luna y la Tierra. Este caso particular lo generalizó para cualquier par de cuerpos. r Dados dos cuerpos cualesquiera de masas m 1 y 2 m2 situados a una distancia r entre sus centros se atraen mutuamente mediante fuerzas de la misma dirección, la de la línea que un sus centros, sentidos opuestos y módulos iguales. u2 m1 F 21 F 12 m m F 21 G 1 2 2 u 2 r u1 m2 m m F 12 G 1 2 2 u 1 r El módulo de las fuerzas es directamente proporcional al producto de las masas e inversamente proporcional a la distancia, entre los centros de los cuerpos, al cuadrado. Obsérvese que el módulo de ambas fuerzas vale lo mismo F G m1 m 2 r u 1 y u 2 son dos vectores unitarios que por convenio se toman de sentido contrario a la fuerza, lo que indica el signo 2 Ambas fuerza son de sentido contrario F 12 F 21 G es la constante de gravitación Universal cuyo valor solo depende de las unidades que le asignemos a -11 2 2 las otras magnitudes y que en SI toma el valor 6,67x10 N m /kg . Como podemos observar es un valor pequeño por lo que las fuerzas entre masas pequeñas serán muy pequeñas, no así entre masas grandes, astros, planetas, etc. que serán grandes. 8 A.3 Estima la masa del Sol sabiendo que la Tierra se encuentra a 1,5x10 km y su periodo de revolución es un 30 año.(Sol:2x10 kg) 1 UA Unidad Astronómica de distancia que equivale a la distancia del Sol a la Tierra: 1,5x10 8 km En realidad Newton utilizó masas puntuales y después demostró que el resultado también es válido para cuerpos extensos cuya masa podemos considerar concentrada en su centro. 2 2 A.4 Estima la masa de la Tierra sabiendo que el periodo de revolución de la Luna es de 27 días, 7 horas y 43 minutos 24 y que la distancia Tierra-Luna es de 380.000 km. (Sol: 6x10 kg) A.5 Una masa puntual de 2 kg está situada en el punto (0,0) y otra de 4 kg en el punto (6,4). Calcula la fuerza sobre ambas masas si las distancias están tomadas en SI.(Sol: F12 8 , 3 10 12 i 5 , 5 10 12 j N; F 12 F 21 ) Si una masa m 1 interacciona con varias masas m 2, m3, m4,… se verá sometida a otras tantas fuerzas siendo la fuerza total F R 1 la suma vectorial de todas ellas: F R 1 F 21 F 31 F 41 Lo que constituye el principio de superposición. A.6 En el punto (0,0) hay una masa m 1= 4 kg, en el punto (4,0) hay una masa m 3=2 kg y en el punto (0,4) hay una masa m2=6 kg. Calcula la fuerza total que actúa sobre cada una de ellas. (Sol: F1 3 , 3 10 F 2 1,8 10 11 i 1, 2 10 10 j N ; F 3 5 ,1 10 11 i 1 ,8 10 11 11 i 10 10 j N; j N) A.7 Dos masas puntuales de 2 kg están situadas en los puntos (0,0) y (4,0) medidos en SI. ¿En qué posición habrá que poner otra masa puntual de 1 kg para que la fuerza total sobre ella sea nula? Si la masa del punto (4,0) fuese de 4 kg ¿En qué posición habrá que poner ahora otra masa puntual de 1 kg para que la fuerza total sobre ella sea nula? (Sol: (2,0), (1’65,0) en SI) Campo de fuerzas En la época de Newton era inconcebible que dos cuerpos, por ejemplo dos planetas, se puedan ejercer fuerzas entre si sin estar en contacto; por otra parte dado que la interacción es instantánea ésta debería propagarse a una velocidad infinita. En el siglo XIX Faraday y Maxwell desarrollaron el concepto de campo como la región del espacio en la que a cada punto se le puede asignar una magnitud física. Si esta magnitud física es vectorial, tendremos un campo vectorial y si es escalar, un campo escalar. Campo gravitatorio Suponemos que cualquier cuerpo por tener masa M modifica el espacio que le rodea confiriendo a cada punto del espacio una propiedad vectorial denominada intensidad de campo gravitatorio ( g ) y que se define como la fuerza que actuaría sobre la unidad de masa en ese punto: F g m g es la intensidad de campo gravitatorio en el punto considerado. F sería la fuerza gravitatoria que actúa sobre un cuerpo de masa m colocado en el punto considerado. Dado que m es un valor positivo, F y g son dos vectores que tienen la misma dirección y sentido F m g 2 Las unidades de g serán N/kg o m/s . g1 Si tenemos en cuenta que antes hemos definido: F G M m r tendremos que: g G M m r 2 u o bien m 2 g2 u gi M g G 2 u r g3 g4 g5 El módulo de g solo depende de la distancia del punto al centro del campo. El campo gravitatorio creado por una masa M es un campo de fuerzas central ya que las fuerzas apuntan al centro de la masa que crea el campo. Si tenemos un sistema de varios cuerpos M1, M2, M3 …, la intensidad del campo en un punto será la suma vectorial de las intensidades de cada campo g g 1 g 2 g 3 , lo que constituye el principio de superposición. A.8 En el punto (0,0) tenemos una masa de 2 kg. a) Determina g para el punto (4,6). (Sol: g 1, 4 10 12 i 2 , 2 10 12 j N/kg) 3 b) ¿Qué fuerza actuará sobre un cuerpo de 5 kg situado en el punto (4,6). (Sol: F 7 10 12 i 11 10 12 j N) A.9 En el punto (0,0) tenemos una masa de 5 kg y en el punto (0,4) tenemos una masa de 3 kg. Distancias en SI. a) Calcula la intensidad del campo gravitatorio g en el punto (4,0). (Sol: g 2 , 6 10 11 i 4 , 5 10 12 j N/kg) b) Calcula la fuerza que actuará sobre una masa de 10 kg situada en el punto (4,0). (Sol: F 2 , 6 10 10 i 4 , 5 10 11 j N) m Una forma de visualizar el campo gravitatorio es mediante las líneas de campo que son líneas imaginarias tangentes a los vectores intensidad en todos puntos. A las líneas de campo se les dota del sentido hacia el centro de la masa crea el campo, igual que los vectores g. En cada zona del espacio la densidad de los que líneas de campo debe ser proporcional a la intensidad del campo. En el caso del campo creado por dos masas hemos de tener en cuenta que el vector campo gravitatorio g en cada punto es la suma vectorial de los vectores correspondientes a cada campo gravitatorio. g2 g1 gT m1 m2 A.10 Calcula la posición, de la línea que une los centros de la Tierra y la Luna, en la que el campo gravitatorio es nulo. (Sol: a 5 3,4x10 km de la Tierra) DATOS: MT=60ML; rTL=380.000 km Trabajo de la fuerza gravitatoria Supongamos que una masa m se desplaza desde el punto A hasta el punto B dentro del campo gravitatorio creado por una masa M. Este desplazamiento lo podemos realizar por infinitos caminos pero elegimos el camino APB. Por tanto podemos expresar: B Q F W AB W AP W PB Si tenemos en cuenta que F es una fuerza variable y recordamos la definición de trabajo: F M dW F d r F dr cos dr dr A m P y lo aplicamos a los dos tramos, nos daremos cuenta que W PB 0 puesto que la fuerza F y el desplazamiento d r son perpendiculares entre si y Cos 90º=0. Para el tramo AP: rP W AP rA F dr rP rP FdrCos 180 º rA rA GMm r 2 rP dr GMm rA dr r 2 rP GMm 1 1 1 GMm r rA rA rP si tenemos en cuenta que los módulos rP rB podemos escribir que W AP W AB W AB 1 1 GMm rA rB GMm rA GMm rB Como podemos observar: El trabajo para trasladar la masa m desde el punto A hasta el punto B sólo depende de las posiciones de estos puntos y no depende del camino seguido; característica ésta que corresponde a las fuerzas conservativas. En cada punto del campo podemos asignar al sistema una propiedad escalar que denominamos energía potencial gravitatoria cuyo valor viene dado por E p G M m que en el SI se mide en J. r La energía potencial gravitatoria es nula para r=∞. Para cualquier otra posición el valor de la energía potencial gravitatoria es negativa, lo que se interpreta como la energía necesaria para llevar m a una posición r=∞ de la masa M que crea el campo gravitatorio. 4 Si soltamos la masa m, la interacción gravitatoria haría que se acercara a la M disminuyendo la energía potencial gravitatoria del sistema; es decir, espontáneamente la masa m se dirige hacia energías potenciales decrecientes. Finalmente podemos expresar la conclusión anterior: W AB ( E pB E pA ) E p El trabajo realizado por la fuerza gravitatoria sobre el cuerpo de masa m será positivo cuando m se dirige hacia energías potenciales decreciente. También se dice trabajo realizado por el campo. El trabajo realizado por la fuerza gravitatoria sobre el cuerpo de masa m será negativo cuando m se dirige hacia energías potenciales crecientes. También se dice trabajo realizado contra el campo o que ha sido realizado por una fuerza exterior. 28 A.11 Calcula la energía potencial gravitatoria del sistema formado por la Tierra y la Luna. (Sol: -7,8x10 -11 2 2 24 22 DATOS: G=6,67x10 Nm /kg ; MT=6x10 kg; ML=7,4x10 kg; rTL=380000 km J) A.12 Dos masa de 2 kg y 6 kg se encuentran a 1 m de distancia. -10 a) Calcula la energía potencial del sistema. (Sol: -8x10 J) -10 b) ¿Qué trabajo habrá que realizar para separarlas a 2 m de distancia? (Sol: -4x10 J) A.13 Una masa se desplaza desde un punto en el que energía potencial es de – 400 J hasta otro en el que la energía potencial es de -1000 J ¿Qué trabajo se ha realizado? (Sol: 600 J) Si el sistema gravitatorio está formado por varias masas, la energía potencial respecto de una de ellas es la suma de la energías potenciales de dicha masa respecto de las demás. Ep1=Ep12+ Ep13 + Ep14 + …. A.14 En el punto (0,0) hay una masa de 2 kg, en el punto (0,4) hay una masa de 6 kg. -10 a) Calcula la energía potencial de una masa de 1 kg situada en el punto (4,0). (Sol: -1x10 J) -10 b) ¿Qué trabajo habrá que realizar para llevar la masa de 1 kg hasta el infinito? (Sol: -1x10 J) Potencial gravitatorio en un punto (V) Acabamos de ver que una masa m situada en el campo gravitatorio, creado por otra masa M, a una distancia r de M, tiene una energía potencial E p GMm . A ese punto del campo le podemos asignar una propiedad escalar que es r independiente de la masa que coloquemos y que solo depende de la masa M y de la distancia r. Se define el potencial de campo (V) en un punto como la energía potencial por unidad de masa situada en ese punto. g GMm V E p m sustituyendo V r V finalmente GM m V1 r V2 V3 V4 El potencial de campo gravitatorio en un punto es siempre negativo. El potencial de campo gravitatorio será nulo en r=∞ El potencial de campo gravitatorio en un punto se mide en el SI en J/kg. Todos los puntos que se encuentra a igual distancia del centro de la masa M que crea el campo están a igual potencial determinando superficies equipotenciales. El campo gravitatorio también se puede visualizar mediante superficies equipotenciales. Antes hemos visto que W AB E p ( E pB E pA ) ( m V B m V A ) m (V B V A ) m V es decir: W AB m V y E p m V Al igual que antes, podemos decir que: El trabajo realizado por la fuerza gravitatoria sobre el cuerpo de masa m será positivo cuando m se dirige hacia potenciales decreciente. El trabajo realizado por la fuerza gravitatoria sobre el cuerpo de masa m será negativo cuando m se dirige hacia potenciales crecientes. El trabajo realizado entre dos puntos equipotenciales será nulo. Si el sistema gravitatorio está formado por varias masas M1, M2, M3, …, el potencial de campo en un punto del campo será la suma de los potenciales debidos a cada masa. V=V1+V2+V3+ … 5 A.15 Tenemos una masa de 200 kg situada en el punto (2,0) -9 -9 a) Calcula el potencial gravitatorio en el punto A(6,0) y en el punto B(10,0) (Sol: V A=-3,3x10 J/kg; VB=-1,7x10 J/kg) -9 b) Calcula la energía potencial de una masa de 2 kg situada en los puntos del apartado anterior. (Sol: E PA=-6,6x10 J; -9 EPB=-3,4x10 J) -9 c) Calcula el trabajo necesario para llevar la masa de 2 kg desde el punto A hasta el punto B. (Sol: -3,2x10 J) A.16 En el punto A(0,0) tenemos una masa de 10 kg y en el punto B(4,0) tenemos una masa de 20 kg. Distancias en SI. -10 -10 a) Calcula el potencial de campo en los puntos C(0,4) y D(4,4) (Sol: VC=-4,1x10 J/kg; VD=-4,5x10 J/kg) -10 b) Calcula el trabajo para desplazar una masa de 4 kg desde el punto D al punto C. (Sol: -1,6x10 J) Campo gravitatorio terrestre La Tierra puede considerarse que tiene forma esférica y una distribución de masa homogénea por lo que la intensidad del campo gravitatorio g T es perpendicular a la superficie de la Tierra y dirigida hacia el centro. Su módulo en la superficie de la Tierra será: gT G M R T que se mide en N/kg o m/s 2 2 24 A.17 Calcula el valor de g en un punto de la superficie terrestre. DATOS:MT=5,98x10 kg; RT=6370 km (Sol: 9,8 N/kg) Sin embargo a medida que nos alejamos de la superficie terrestre g toma valores menores. Así para una altura h sobre la superficie terrestre: g h G M T ( RT h ) 2 Es evidente que el campo gravitatorio terrestre será nulo en el infinito. A.18 Calcula g para las siguientes alturas sobre la superficie terrestre: 10 km, 100 km, 1000 km y 10000 km. (Sol: 9,8 N/kg; 9,5 N/kg;…) http://www.sc.ehu.es/sbweb/fisica/celeste/kepler3/kepler3.html Debes recordar que llamamos peso de un cuerpo a la fuerza con que la Tierra lo atrae p m g . A.19 Establece la relación entre gh a cierta altura h sobre la superficie terrestre y g en la superficie terrestre. (Sol: 2 2 gh=g(RT /(RT+h) ) A.20 ¿Cuál es el peso de tu cuerpo en la superficie terrestre? ¿Cuál será el peso de tu cuerpo a una distancia sobre la superficie terrestre igual al radio de la Tierra? Es evidente que estas consideraciones sobre el campo gravitatorio terrestre son ampliables a cualquier otro astro del universo, la Luna, planetas, etc. A.21 Calcula g en la superficie de la Luna y Marte. Busca los datos necesarios.(Sol: 1,6 N/kg; 3,7 N/kg) A.22 Si la Tierra atrae a la Luna y la Luna atrae a Tierra ¿por qué no se juntan? A.23 Habrás visto las imágenes de los astronautas “flotando”. Da una explicación. Movimiento de planetas y satélites Llamamos órbita a la trayectoria que realiza un móvil alrededor de un cuerpo central. Si consideramos que cualquier masa m que se mueve alrededor de otra masa M central lo hace según un MCU, entonces, como hemos visto, se 2 verá sometido a una fuerza centrípeta Fc= m(v /r). Esta fuerza es de naturaleza 2 gravitatoria: Fg=GMm/r por lo tanto los valores de estas dos expresiones deben ser iguales y la rapidez del objeto de masa m en órbita será: v orb G M rorb como podemos observar la velocidad en órbita sólo depende del radio de la órbita pero no depende de la masa del objeto. Por otra parte, el tiempo que tarda el objeto en describir una órbita (el periodo) será: 6 T 2 rorb sustituyendo el valor encontrado para vorb ; T v orb 3 2 G M r 2 orb Finalmente, si tenemos en cuenta que Fc está dirigida hacia el centro de la órbita y que Fg tiene la dirección de la recta que une los centros de los cuerpos, podemos deducir que el centro de la órbita y el centro del cuerpo de masa M coinciden. A.24 Calcula la velocidad de la Tierra alrededor del Sol. (Sol: 107232 km/h) A.25 La ISS realiza órbitas circulares alrededor de la Tierra a 338 km sobre la superficie del planeta. R T=6370 km. a) Calcula la velocidad de la estación en la órbita. (Sol: 7710 m/s) b) Calcula el tiempo que tarda en describir una órbita. (Sol: 5468 s) La Tierra, además de su satélite natural, la Luna, tiene otros muchos satélites llamados artificiales porque han sido lanzados por los hombres. Estos satélites artificiales, según su función, se encuentran en diferentes órbitas tanto en inclinación respecto del eje de la Tierra como en altura sobre su superficie. Los satélites dedicados a la investigación y observación de la superficie de la Tierra se encuentras en órbitas bajas, entre 300 o 400 km, por el contrario los satélites de comunicaciones para cumplir su función deben estar en una órbita tal que el satélite se encuentre siempre en la vertical sobre el mismo punto de la superficie terrestre, órbita geoestacionaria. Para que esto ocurra tiene que cumplirse que el plano de su órbita sea perpendicular al eje de rotación de la Tierra y además su centro debe coincidir con el de la Tierra (plano ecuatorial); por otra parte su periodo de revolución debe coincidir con el periodo de rotación de la Tierra, es decir 24 horas aproximadamente. A.26 Calcula a qué distancia sobre la superficie terrestre se encuentra un satélite geoestacionario de comunicaciones. (Sol: 35880 km) a) Calcula su velocidad. (Sol: 3072 m/s) Energía de un satélite Un satélite es un objeto de masa m que se mueve alrededor de un objeto central por lo que tiene energía cinética y energía potencial al estar sometido a la fuerza gravitatoria. Desde el punto de vista energético debe verificarse: W roz E p Ec Ahora bien, dado que los satélites (y los planetas) se mueven en el espacio vacío, W roz 0 o lo que es lo mismo: E p Ec 0 (E p E c constante) De donde se deduce que la energía mecánica de un satélite es un valor constante: E c E p si tenemos en cuenta que la rapidez en órbita es v orb Ec E p GMm 2r G M m v 2 2 GMm y r entonces: rorb GMm GMm r 2r A.27 Calcula la energía cinética, potencial y mecánica del satélite de comunicaciones del ejercicio A.26 si tiene una 10 10 10 masa de 4600 kg. (Sol: 2,17x10 J; -4,34x10 J; -2,17x10 J) A.28 Un meteorito de 10 kg se encuentra en reposo a una distancia de la superficie de la Tierra que es igual a 5 veces el radio de la Tierra. DATOS: Usa la masa de la Tierra, el radio de la Tierra y G. 8 a) Calcula la energía mecánica del meteorito. (Sol: -1.05x10 J) b) ¿A qué velocidad se producirá el impacto del meteorito sobre la superficie de la Tierra? (Sol: 10,2 km/s) Velocidad de escape Supongamos que queremos lanzar (no propulsar) un cuerpo de masa m desde la superficie de un astro de masa M p y radio rp hasta el infinito, es decir hasta que se desligue del campo gravitatorio de M p y quede en reposo. Si prescindimos del rozamiento con los gases de la atmósfera, se verificará que: W roz E p E c 0 o bien ( E p E p sup ) ( E c E c sup ) 0 y dado que E p E c 0 nos queda que E p sup E c sup 0 y sustituyendo sus valores G M rp v escape 2 G M p p m m v 2 0 de donde se deduce que 2 que es la denominada velocidad de escape. rp 7 Observa que la velocidad de escape no depende de la masa del objeto lanzado y sólo depende de las propiedades del planeta. Es decir, lanzando verticalmente un objeto desde la superficie de un planeta con su correspondiente velocidad de escape, el objeto podría llegar hasta el infinito. De existir rozamiento con la atmósfera la velocidad de escape no desligaría al cuerpo del campo gravitatorio y este volvería al planeta u orbitaría alrededor de él. Este mismo planteamiento sería, también, aplicable a un objeto que se encuentre orbitando con radio r 0 en vez de la superficie del un planeta. A.29 Calcula la velocidad de escape de la Tierra, de la Luna y de Marte. (Sol: 11191 m/s; 2374 m/s; 5019 m/s) Lanzamiento de satélites Para lanzar un satélite hasta una orbita, desde la superficie de la Tierra, habrá que realizar un trabajo: W E p Ec (E E porb ) ( E corb E c sup ) p sup Para simplificar los cálculos supondremos que E c sup 0 aunque no es cierto ya que en la superficie de la Tierra el satélite se mueve a la misma velocidad que ésta. Tampoco consideraremos el rozamiento con el aire de la atmósfera. Por tanto: GMm GMm GMm W rorb rT 2 rorb GMm 1 1 GMm 2 rorb rT GMm 2 rorb rT A.30 Calcula la energía necesaria para lanzar un satélite de 250 kg hasta una órbita de 500 km sobre la superficie de 9 la Tierra. DATOS: Usa la masa de la Tierra, el radio de la Tierra y G. (Sol: 9x10 J) Cambio de órbita de satélite Los satélite de baja altura necesitan de vez en cuando corregir su órbita en altitud como consecuencia del leve rozamiento con las altas capas de la atmósfera, también necesitan cambiar de órbita cuando deciden volver a la superficie del planeta. Para ello disponen de cohetes propulsores a tal fin. Supongamos que un satélite de masa m desea pasar de una órbita 1 hasta una órbita 2. W E p Ec (E porb 2 E porb 1 ) ( E corb 2 E corb 1 ) A.31 Calcula el trabajo necesario para elevar la ISS, que tiene una masa de 454 Tn, desde una órbita de 350 km 12 hasta otra de 400 km sobre la superficie de la Tierra. (Sol: 1x10 J) http://www.solarviews.com/span/homepage.htm ASTRO Sol Mercurio Venus Tierra Luna Marte Júpiter Saturno Urano Neptuno Plutón RAstro (km) 695000 2439.7 6051.8 6378.14 1737.4 3397.2 71492 60268 25559 24746 1160 MASA (kg) 30 1.99x10 23 3.30x10 24 4.87x10 24 5.98x10 22 7.35x10 23 6.42x10 27 1.90x10 26 5.69x10 25 8.69x10 26 1.02x10 22 1.29x10 Tórbita (días) Trotación(días) Rórbita (km) 6 57,91x10 6 108,2x10 6 149,6x10 3 384x10 6 228x10 6 778x10 9 1,43x10 9 2,87x10 9 4,5x10 9 5,9x10 88 224,7 365,256 27,32 687 4333 10760 30685 60190 90800 58,6 243 0.997 27,32 1,03 0,41 0,44 0,72 0,67 6.4 8 AYUDAS PARA LA RESOLUCIÓN DE LOS EJERCICIOS DEL TEXTO Lee atentamente el ejercicio y piensa que está relacionado con los párrafos anteriores. Piensa que en los casos más sencillos resolverás el ejercicio aplicando alguna ecuación del párrafo anterior. Si tienes dificultad con el planteamiento físico del ejercicio, consulta la ayuda correspondiente. Si no consigues resolver el ejercicio, plantéale al Profesor tus dificultades el próximo día (no al cabo de una semana o de un mes) A.1 Debes buscar (o recordar) el periodo revolución de la Tierra alrededor del Sol así como la distancia media de la Tierra al Sol. Después aplica la tercera ley de Kepler para la Tierra y Marte y deduce la distancia media de Marte al Sol. Para la segunda pregunta, aplica la tercera ley de Kepler para la Tierra y Venus. A.2 Suponiendo que realizan un MCU, recuerda que v r 2 r y aplícalo a ambos casos, la Tierra y Marte. T A.3 Recuerda que la fuerza gravitatoria que ejerce el Sol sobre la Tierra es F G M S M 2 T y que se trata de una fuerza rS T central F M T 2 rS T Iguala ambas expresiones, simplifica y calcula. A.4 Este ejercicio es similar al anterior. A.5 Debes comenzar dibujando un esquema de la situación sobre un eje de coordenadas. Las fuerzas sobre ambas masas son de m m tipo gravitatorio y opuestas. Al ser fuerzas, se trata de vectores: F F cos i F sen j donde F G 1 2 2 . Para r la fuerza que actúa sobre la masa en (0,0), primero tienes que deducir r por Pitágoras y α por trigonometría, y después construir el vector. La fuerza que actúa sobre la otra masa es la opuesta de la anterior. A.6 Dibuja un esquema de la situación. En este caso, al haber tres masas, sobre cada una de ellas actúan dos fuerzas debidas a las otras dos masas. Calcula, como antes, estas fuerzas y recuerda que la fuerza total sobre cada masa es la suma (vectorial) de las fuerzas que actúan sobre ella (principio de superposición) A.7 Dibuja un esquema de la situación y sobre él discute cuál será la posición (x,0) teniendo en cuenta que sobre la masa de 1 kg actúan dos fuerzas opuestas (con el mismo módulo). En el segundo caso, ocurre lo mismo pero al ser la otras dos masas diferentes tendrás que pensar que el punto (x,0) estará más lejos de la masa más grande. Al ser los dos módulos iguales tendrás que plantear una igualdad que resolverás mediante una ecuación de segundo grado. De las dos posibles soluciones tendrás que discutir cuál es la correcta según el planteamiento que hayas realizado. A.8 Dibuja un esquema de la situación. Este ejercicio es similar a A.5 pero ahora tenemos que calcular m g g cos i g sen j siendo g G 2 y α el ángulo que forma el vector g con +X. Para calcular el apartado b) r bastará con que tengas en cuenta que F m g A.9 Dibuja un esquema de la situación sobre un eje de coordenadas. En el punto (4,0) calcularás dos vectores g debido a cada una de las masas. La intensidad en ese punto la determinarás por el principio se superposición. La fuerza sobre la masa de 10 kg en ese punto es inmediata. A.10 Dibuja un esquema de la situación. La resolución es similar a A.7 A.11 Aplica la expresión de la energía potencial gravitatoria que hemos deducido. A.12 El apartado a) es similar al ejercicio A.11. En el apartado b) tendrás que calcular la energía potencial gravitatoria en la nueva posición y aplicar W E p A.13 Aplica W E p A.14 Dibuja un esquema de la situación. Determina las distancias entre las masas y calcula la energía potencial gravitatoria de la masa de 1 kg respecto de las otras dos y aplica el principio de superposición. Para el apartado b) aplica W E p A.15 Aplica el cálculo del potencial en las dos posiciones V GM r . Para el apartado b) aplica E p m V en ambas posiciones. Para el apartado c) aplica W m V 9 A.16 Dibuja un esquema de la situación. Aplica el principio de superposición para calcular el potencial gravitatorio en C y en D. Para el apartado b) aplica W m V A.17 Aplica g G M T 2 rT A.18 Aplica en cada caso g h G M T ( RT h ) 2 y ten en cuenta que R T h se debe expresar en metros y busca los datos que te hagan falta. gh A.19 Plantea la relación y simplifícala. g A.20 Primero determina tu masa en una balanza de baño, luego aplica p=mg en las dos situaciones (g=9,8 N/kg en la superficie de la Tierra; g A.21 Aplica g G M r A.24 Aplica v orb 2 G M T (2 RT ) 2 en la segunda posición) en ambos casos. Busca los datos que necesites. G M ; busca los datos que necesites. Recuerda que este valor lo estimaste en A.2 rorb A.25 Para a) aplica v orb A.26 Para a) aplica T G M 2 rorb ; para b) aplica T rorb 2 G M o bien T v orb 2 G M 3 2 rorb 3 2 despejando r, pero ten en cuenta que el resultado que obtienes es la distancia rorb al centro de la Tierra y que se te pide la distancia sobre la superficie de la Tierra. Para b) aplica v orb A.27 Con los datos obtenidos en A.26 aplica E c m v 2 2 y Ep GMm r G M rorb ; finalmente Em=Ec+Ep A.28 Calcula la energía del meteorito teniendo en cuenta que está en reposo y que E m=Ec+Ep. Para el apartado b) debes suponer que no hay rozamiento con la atmósfera y hacer un balance energético entre la posición en órbita y la posición en la superficie de la Tierra: ∆Ep+∆Ec=0 A.29 Aplica en cada caso v escape 2 G M p rp A.30 Te preguntan el trabajo para poner en órbita un satélite. Realizando un balance energético: W=∆Ep+∆Ec entre la superficie y la órbita. Tendrás que suponer que la energía cinética en la superficie es nula. También tendrás que calcular la velocidad en órbita del satélite para poder calcular su energía cinética en órbita. A.31 Tendrás que hacer un balance energético similar al del ejercicio anterior. Te preguntan W. 10 EJERCICIOS PROPUESTOS EN LAS PRUEBAS DE ACCESO +25 1. a) Enuncie la ley de Gravitación Universal, escriba su expresión matemática e indique las magnitudes físicas que intervienen en la misma. 1.b) Si todos los cuerpos del Universo se atraen, ¿por qué no se aprecia la atracción entre dos objetos cualesquiera de la Tierra? 2.a) Enunciado de la ley de Gravitación Universal. Expresión matemática de dicha ley indicando las magnitudes físicas que aparecen en ella. 2.b) ¿Es cierto que el peso y la masa de un cuerpo son magnitudes físicas diferentes? 3) El radio de la Tierra es aproximadamente 6370 km mientras que el de Marte es de 3440 km. 3.a) ¿Cuánto vale la gravedad en la superficie de Marte? (Sol: 3,7 N/kg) 3.b) Si un objeto pesa 200 N en la Tierra ¿cuál es su peso en Marte? (Sol: 75,5 N) DATOS: gravedad en la superficie de la Tierra g=9,8 N/kg; la masa de Marte es 0,11 veces la masa de la Tierra. 4) ¿Cómo varía el peso de un cuerpo en el camino Tierra-Luna? ¿Varía su masa? ¿Cómo se explica que algunos satélites se quemen al descender a la Tierra y no se quemaron al ascender? 5.) Dos satélites idénticos orbitan en torno a la Tierra, siendo R1 y R2, respectivamente, los radios de sus órbitas (R1 > R2). a) ¿Cuál de los dos satélites se moverá a mayor velocidad? b) ¿Cuál de los dos tendrá mayor energía mecánica? Razone las respuestas. 6.a) Enuncie la ley de Gravitación Universal y defina las magnitudes que aparecen en ella. 6.b) Dos satélites A y B describen órbitas circulares alrededor de la Tierra estando A a una distancia del centro de la Tierra doble que B. Deduzca la relación entre los periodos orbitales de ambos satélites. 11