multiplicadoreslagrange1

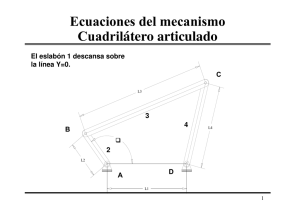
Mecánica Teórica, problema de ejemplo 1.
(por [email protected] . actual. 20.Enero.2009)
En un sistema como el de la figura, una barra de longitud L está apoyada contra una
pared, donde puede deslizarse sin rozamiento. Se trata de resolver este problema (hallar
las ecuaciones del movimiento) empleando el método de los multiplicadores de Lagrange.
Se toma como sistema de coordenadas el de los ejes X,Y representados en la figura. A partir
de ahí, si se considera toda la masa de la barra (supuesta homogénea) concentrada en el punto
P(x,y) de la figura, el movimiento de este punto no es libre en el plano XY, si no que está
restringido por una serie de DOS ligaduras, expresadas de la siguiente manera:
L
sin  [1]
2
L
y  cos [2]
2
Donde es el ángulo que forma la barra con la vertical (ver figura)
x
Tomamos como coordenadas generalizadas de problema: x, y, 

Tenemos entonces un problema de multiplicadores de Lagrange con 3 coordenadas
generalizadas y dos ligaduras. El sistema de ecuaciones diferenciales para las ligaduras lo
podemos expresar de la siguiente forma, diferenciando [1] y [2] respectivamente:
L
cosd  0 [3]
2
L
dy  sin d  0 [4]
2
dx 
Tenemos pues, 2x3=6 coeficientes diferenciales, 3 por cada ligadura, que, identificando desde
[3] y [4] serán…
a1x  1
a1 y  0
a2 x  0
a2 y  1
L
a1   cos
2
L
a2  sin 
2
A partir de aquí construimos el Lagrangiano para las coordenadas generalizadas. Para la
energía cinética, tenemos:
T


1
1
m x 2  y 2  I 2
2
2
Donde I es el momento de inercia de una barra respecto a su punto central, o sea I 
1
mL2
12
Para la energía potencial (gravitatoria respecto el suelo), tenemos:
V  mgy
Y el Lagrangiano queda como:


1
mL2  2
2
2





L ( x , y , x, y ,  )  m x  y 
  mgy
2
24
 d  L
Y las respectivas ecuaciones de Lagrange  
 dt  qk
generalizadas (x,y, …

 L
 
 0  para las tres coordenadas
 qk


 mx  0

m y  g   0
 mL2 
 0

 12
Entonces el sistema de ecuaciones con multiplicadores de Lagrange, para cada una de las dos
ligaduras, queda de la siguiente forma:
Ligadura #1:
mx  1  0

 2
L
 mL

cos  0


1
 12
2
Ligadura #2:
 m y  g   2  0
 2
L
 mL



sen  0
2
 12
2
Teniendo en cuenta las ligaduras y diferenciándolas respecto al tiempo, tenemos…
x
L
L
L
L
sin   x  cos  x   sin  2  cos
2
2
2
2
L
L
L
2

y  cos    y  cos  sin 
2
2
2
Sustituyendo estas expresiones en el sistema de ecuaciones de ligaduras más arriba, obtenemos
los valores de los multiplicadores:


mL
sin  2  cos
2
L
L

2   cos 2  sin   g 
2

2
1 
Para una coordenada generalizada cualquiera, qk, la ecuación de Lagrange con multiplicadores
es:
L d  L
 
qk dt  qk
 n
   l alk  0
 l 1
Para la coordenada generalizada tenemos que:
mL2 
L
L

 L

L
 L
 L
  m  sin  2  cos cos   mg  m  cos 2  sin  sin   
12
2
2

 2
2

 2
 2

5
   2 sin  cos 2  g sin 
6