BUC: Física II. Práctica N 10: El campo magnético.

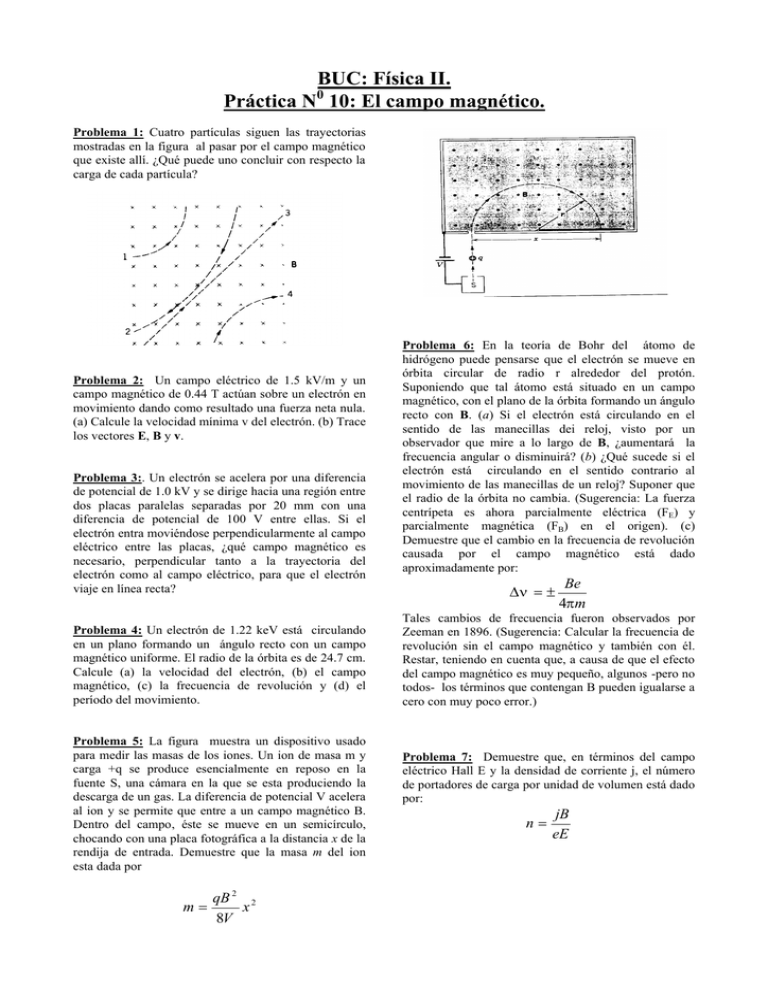
BUC: Física II.
Práctica N 10: El campo magnético.
0
Problema 1: Cuatro partículas siguen las trayectorias
mostradas en la figura al pasar por el campo magnético
que existe allí. ¿Qué puede uno concluir con respecto la
carga de cada partícula?
Problema 2: Un campo eléctrico de 1.5 kV/m y un
campo magnético de 0.44 T actúan sobre un electrón en
movimiento dando como resultado una fuerza neta nula.
(a) Calcule la velocidad mínima v del electrón. (b) Trace
los vectores E, B y v.
Problema 3:. Un electrón se acelera por una diferencia
de potencial de 1.0 kV y se dirige hacia una región entre
dos placas paralelas separadas por 20 mm con una
diferencia de potencial de 100 V entre ellas. Si el
electrón entra moviéndose perpendicularmente al campo
eléctrico entre las placas, ¿qué campo magnético es
necesario, perpendicular tanto a la trayectoria del
electrón como al campo eléctrico, para que el electrón
viaje en línea recta?
Problema 4: Un electrón de 1.22 keV está circulando
en un plano formando un ángulo recto con un campo
magnético uniforme. El radio de la órbita es de 24.7 cm.
Calcule (a) la velocidad del electrón, (b) el campo
magnético, (c) la frecuencia de revolución y (d) el
período del movimiento.
Problema 5: La figura muestra un dispositivo usado
para medir las masas de los iones. Un ion de masa m y
carga +q se produce esencialmente en reposo en la
fuente S, una cámara en la que se esta produciendo la
descarga de un gas. La diferencia de potencial V acelera
al ion y se permite que entre a un campo magnético B.
Dentro del campo‚ éste se mueve en un semicírculo,
chocando con una placa fotográfica a la distancia x de la
rendija de entrada. Demuestre que la masa m del ion
esta dada por
qB 2 2
m=
x
8V
Problema 6: En la teoría de Bohr del átomo de
hidrógeno puede pensarse que el electrón se mueve en
órbita circular de radio r alrededor del protón.
Suponiendo que tal átomo está situado en un campo
magnético, con el plano de la órbita formando un ángulo
recto con B. (a) Si el electrón está circulando en el
sentido de las manecillas dei reloj, visto por un
observador que mire a lo largo de B, ¿aumentará la
frecuencia angular o disminuirá? (b) ¿Qué sucede si el
electrón está circulando en el sentido contrario al
movimiento de las manecillas de un reloj? Suponer que
el radio de la órbita no cambia. (Sugerencia: La fuerza
centrípeta es ahora parcialmente eléctrica (FE) y
parcialmente magnética (FB) en el origen). (c)
Demuestre que el cambio en la frecuencia de revolución
causada por el campo magnético está dado
aproximadamente por:
∆ν = ±
Be
4πm
Tales cambios de frecuencia fueron observados por
Zeeman en 1896. (Sugerencia: Calcular la frecuencia de
revolución sin el campo magnético y también con él.
Restar, teniendo en cuenta que, a causa de que el efecto
del campo magnético es muy pequeño, algunos -pero no
todos- los términos que contengan B pueden igualarse a
cero con muy poco error.)
Problema 7: Demuestre que, en términos del campo
eléctrico Hall E y la densidad de corriente j, el número
de portadores de carga por unidad de volumen está dado
por:
n=
jB
eE
Problema 8: (a) Demuestre que la razón entre el campo
eléctrico Hall E y el campo eléctrico Ec, responsable de
la corriente es
E
B
=
E c neρ
donde ρ es la resistividad del material.
Problema 9: Un alambre de 62.0 cm de longitud y 13.0
g de masa está suspendido por un par de puntas flexibles
dentro de un campo magnético de 440 mT. Determine la
magnitud y dirección de la corriente en el alambre
uniforme de 75.0 mT de magnitud cuya dirección es
paralela a la corriente en el lado de 130 cm de la espira.
(a) Halle la fuerza magnética sobre cada uno de los tres
lados de la espira. (b) Demuestre que la fuerza
magnética total en la espira es cero.
Problema 13: Por un alambre de longitud L pasa una
corriente i. Demuestre que si el alambre tiene la forma
de una bobina circular, el momento de torsión máximo
en un campo magnético dado se desarrolla cuando la
bobina tiene solo una vuelta y el momento de torsión
máximo tiene la magnitud
τ =
1 2
L iB
4π
Problema 14:. Por una espira circular de alambre cuyo
radio es de 16.0 cm pasa una corriente de 2.58 A. Esta
colocada de tal modo que la normal a su plano forma un
ángulo de 41.0o con un campo magnético uniforme de
1.20 T.
(a) Calcule el momento dipolar magnético del anillo.
(b) Determine el momento de torsión sobre la espira.
necesaria para suprimir la fuerza de tensión en los
conductores de apoyo.
Problema 10: Un alambre de metal de masa m se
desliza sin fricción sobre dos rieles horizontales
espaciados a una distancia d. La vía está dentro de un
campo magnético vertical uniforme B. Una corriente
constante i fluye desde el generador G a lo largo de un
riel, a través del alambre, y de regreso al otro riel. Halle
la velocidad (rapidez y dirección) del alambre en
función del tiempo, suponiendo que está en reposo en t
= 0.
Problema 11: Un conductor largo y rígido, que se
encuentra a lo largo del eje x, porta una corriente de 5.0
A en la dirección -x. Está presente un campo
magnético B, dado por B = 3i +8x2j, con x en metros y
B en mT. Calcule la fuerza sobre el segmento de 2.0 m
del conductor que se encuentra entre
x= 1.2m y x=3.2m.
Problema 12: Una espira de una sola vuelta, por la que
fluye una corriente de 4.00 A, tiene la forma de un
triángulo rectángulo, siendo sus lados de 50 cm, 120 cm
y 130 cm. La espira está dentro de un campo magnético
Problema 15: Dos anillos circulares concéntricos, de
radios 20.0 y 30.0 cm, en el plano xy, portan cada uno
de ellos una corriente de 7.00 A en el sentido de las
manecillas del reloj. (a) Halle el momento magnético
neto de este sistema. (b) Repita para el caso en que la
corriente en el anillo exterior se invierte.
BUC: Física II.
Práctica N0 11: La ley de Ampere.
Problema 1: Un alambre recto y largo conduce una
corriente de 48.8 A. Un electrón, que viaja a 1.08 x 107
m/s, está a 5.20 cm del alambre. Calcule la fuerza que
actúa sobre el electrón si su velocidad se dirige (a) hacia
el alambre, (b) paralela a la corriente y (c) en ángulo
recto con las direcciones definidas por (a) y (b).
iguales i en la misma dirección. Halle el campo
magnético en P, a medio camino entre las bobinas.
Problema 2: Dos alambres paralelos largos están a
8.10 cm de separación. ¿Qué corrientes iguales deben
fluir en los alambres si el campo magnético a la mitad
entre ellos ha de tener una magnitud de 296 µT?
Problema 3: Dos alambres paralelos rectos y largos,
separados por 0.75 cm, son perpendiculares al plano de
la página como se muestra en la figura. El alambre W,
conduce una corriente de 6.6 A hacia la página. ¿Cuál
debe ser la corriente (magnitud y dirección) en el
alambre W2 para que el campo magnético resultante en
el punto P sea cero?
Problema 4:. La figura muestra un tramo de alambre
que conduce una corriente i y está doblado formando
una bobina circular de una vuelta. En la figura b, el
mismo tramo de alambre se ha doblado más, para formar
una espira doble de radio más pequeño. (a) Si Ba y Bb
son las magnitudes de los campos magnéticos en los
centros de las dos espiras, ¿cuál es la razón Ba/Bb? (b)
¿Cuál es la razón de sus momentos dipolares, µa/µb?
Problema 6: Considere el circuito de la figura. Los
segmentos curvos son arcos de círculo de radios a y b.
Los segmentos rectos están a lo largo de los radios.
Halle el campo magnético B en P, suponiendo una
corriente i en el circuito.
Problema 7: Un segmento recto de alambre de longitud
L conduce una corriente i. Demuestre que el campo
magnético B asociado con este segmento a la distancia
R del segmento a lo largo de una bisectriz perpendicular
está dado en magnitud por
µ 0i
L
2
2πR ( L + 4 R 2 )1 / 2
Demuestre que esta expresión se reduce a un resultado
esperado cuando L →∞.
B=
Problema 5: La figura muestra un arreglo conocido
como bobina de Helmholtz. Consta de dos bobinas
circulares coaxiales cada una de N vueltas y radio R,
separadas por una distancia R Conducen corrientes
Práctica N0 11: La ley de Ampere
1
Problema 8: La figura muestra la sección transversal
de una cinta larga y delgada de anchura w que está
conduciendo hacia adentro de la página una corriente
total i distribuida uniformemente. Calcule la magnitud y
la dirección del campo magnético B en un punto P en el
plano de la cinta a una distancia d de su extremo.
(Sugerencia: Imagine que la cinta está construida de
muchos alambres paralelos, largos y delgados.)
Problema 9: (a) Un alambre en forma de un polígono
regular de n lados esta justamente encerrado por un
círculo de radio a. Si la corriente por este alambre es i,
demuestre que el campo magnético B en el centro del
círculo está dado, en magnitud, por
B=
Problema 12: Considérese un alambre cilíndrico largo
de radio R que conduce una corriente i distribuida
uniformemente en su sección transversal. ¿A qué dos
distancias del eje del alambre la intensidad del campo
magnético debido a la corriente es igual a la mitad del
valor en la superficie?
Problema 13: Demuestre que un campo magnético
uniforme B no puede caer abruptamente a cero
conforme uno se mueve en ángulo recto con él, como se
indica por la flecha horizontal a través del punto a en la
figura. (Sugerencia: Aplique la ley de Ampere a la
trayectoria rectangular mostrada por las líneas de
trazos.) En los imanes reales siempre ocurre el "efecto
de borde" de las líneas de B, lo cual significa que B
tiende a cero en forma gradual. Modifique las líneas de
B en la figura para indicar una situación más realista.
µ 0 ni
tan (π / n)
2πa
(b) Demuestre que cuando n →∞ este resultado se
aproxima al de una espira circular. (c) Encuentre el
momento dipolar del polígono.
Problema 10: Un disco delgado de plástico de radio R
tiene una carga q distribuida uniformemente en su
superficie. Si el disco gira con una frecuencia angular w
alrededor de su eje, demuestre que (a) el campo
magnético en el centro del disco es
B=
µ 0 wq
2πR
y (b) el momento dipolar magnético del disco es
wqR 2
µ=
4
(Sugerencia: El disco que gira es equivalente a un
conjunto de espiras de corriente.)
Problema 14: La figura muestra la sección transversal
de un conductor cilíndrico hueco de radios a y b, que
conduce una corriente i uniformemente distribuida. (a)
Usando el anillo amperiano circular mostrado, verifique
que B(r) para el intervalo b < r < a está dado por
µ 0i
(r 2 − b 2 )
B=
r
2π (a 2 − b 2 )
(b) Compruebe esta fórmula para los casos especiales en
los que r =a, r = b y b=0. (c) Suponga que a = 2.0 cm,
b= 1.8 cm e i =100 A y grafique B(r) en el intervalo 0 <
r < 6 cm.
Problema 11: La figura muestra un alambre largo que
conduce una corriente i1. La espira rectangular conduce
una corriente i2. Calcule la fuerza resultante que actúa
sobre la espira. Suponga que a = 1.10 cm, b = 9.20 cm,
L = 32.3 cm, i1=28.6 A e i2 =21.8A.
Problema 15: La figura muestra la sección transversal
de un conductor largo del tipo llamado cable coaxial, de
radios a, b y c. En los conductores existen corrientes i
iguales pero antiparalelas, distribuidas uniformemente.
Deduzca expresiones para B(r) en los intervalos (a) r <
c, (b) c < r < b, (c) b < r < a, y (d ) r > a. (e) Pruebe
Práctica N0 11: La ley de Ampere
2
estas expresiones para todos los casos especiales que se
le ocurran. (f) Suponga que a = 2.0 cm, b = 1.8 cm, c =
0.40 cm e i = 120 A, y grafique B(r) dentro del intervalo
0 < r < 3 cm.
Problema 16: Un conductor consta de un número
infinito de alambres adyacentes, cada uno infinitamente
largo y conduciendo una corriente i0. Demuestre que las
líneas de B son como se representan en la figura y que B
para todos los puntos arriba y abajo de la lámina infinita
de corriente está dado por
B(r ) =
µ 0 ni
2
en donde n es el numero de alambres por unidad de
longitud.
Problema 17: La densidad de corriente a lo largo de un
alambre cilíndrico, largo, sólido, de radio a está en
dirección del eje y varía linealmente con la distancia
radial r relativo al eje de acuerdo con j=j0r/a. Determine
el campo magnético en el interior del alambre. Exprese
la respuesta en función de la corriente total i que fluye
por el alambre.
Problema 18: Un solenoide de 95.6 cm de largo tiene
un radio de 1.90 cm, un devanado de 1230 vueltas y
conduce una corriente de 3.58 A. Calcule la intensidad
del campo magnético en el interior del solenoide.
Problema 19: Un toroide que tiene una sección
transversal cuadrada de 5.20 cm de lado y un radio
interior de 16.2 cm tiene 535 vueltas y conduce una
corriente de 813 mA. Calcule el campo magnético en el
interior del toroide en (a) el radio interior y (b) el radio
exterior del toroide.
Práctica N0 11: La ley de Ampere
3
BUC: Física II.
Práctica N 12: La ley de inducción de Faraday.
0
Problema 1: Una antena circular de televisión de UHF
(frecuencia ultra-alta) tiene un diámetro de 11.2 cm El
campo magnético de una señal de TV es normal al plano
de la espira y, en un instante de tiempo, su magnitud está
cambiando a razón de 157 mT/s. El campo es uniforme.
Halle la fem en la antena.
segundos. Halle la fem en la espira cuadrada en t= 3.0 s.
Problema 6: En la figura, el cuadrado tiene lados de
2.0 cm de longitud. Un campo magnético apunta hacia
afuera de la página; su magnitud está dada por B= 4t2y,
donde B está en teslas, t en segundos e y en metros.
Determine la fem alrededor del cuadrado en t=2.5 s y dé
su dirección.
Problema 2: En la figura, el flujo magnético a través de
la espira mostrada aumenta gradualmente de acuerdo
con la relación Φ B (t ) = 6t + 7t donde Φ B está en
miliwebers y t está en segundos. (a) ¿Cuál es el valor
absoluto de la fem inducida en la espira cuando t=2.0
seg.? (b) ¿Cuál es la dirección de la corriente que pasa
por el resistor?
2
Problema 3: Una antena de cuadro de área A y
resistencia R es perpendicular a un campo magnético
uniforme B. El campo cae linealmente a cero en un
intervalo de tiempo ∆t. Halle una expresión para la
energía interna total disipada en la antena.
Problema 4: En la figura del problema 2, sea Φ B (0)
el flujo para la espira en el tiempo t. Luego hagamos
que el campo magnético B varíe de un modo continuo
pero no especificado, tanto en magnitud como en
dirección, de modo que al tiempo t el flujo está
representado por Φ B (t ) . (a) Demostrar que la carga
neta que ha pasado por el resistor R en el tiempo t es
q (t ) =
1
(Φ B (0) − Φ B (t )) independientemente de
R
la manera que haya cambiado B. (b) Si en algún instante
en particular Φ B (t ) = Φ B (0) entonces q(t)=0. ¿Es
necesariamente cero la corriente inducida en el intervalo
de tiempo 0 a t?
Problema 5: En la situación mostrada en la figura a=12
cm, b=16 cm. La corriente en el alambre recto y largo
está dada por i=4.5t2-10t, donde i está en amperes y t en
Práctica N012: La ley de inducción de Faraday
Problema 7: La figura muestra una barra conductora de
longitud L que, tirando de ella, es atraída a lo largo de
rieles conductores horizontales, carentes de fricción, a
una velocidad constante v. Un campo magnético vertical
uniforme B ocupa la región en que se mueve la barra.
Supóngase que L=10.8 cm, v=4.86 m/s y B=1.18 T. (a)
Halle la fem inducida en la barra. (b) Calcule la
corriente en la espira conductora. Suponga que la
resistencia de la barra es de 415 mΩ y que la resistencia
de los rieles es despreciablemente pequeña (c) ¿A qué
velocidad se está generando la energía interna en la
barra? (d) Determine la fuerza que debe aplicarse por un
agente externo a la barra para mantener su movimiento
(e) ¿A qué velocidad esta fuerza realiza trabajo sobre la
barra? Compare esta respuesta con la respuesta dada en
(c).
Problema 8:. En la figura, una barra conductora de
masa m y longitud L se desliza sin fricción sobre dos
rieles horizontales largos. Un campo magnético vertical
uniforme B ocupa la región en que la barra está en
libertad de moverse. El generador G suministra una
corriente i constante que fluye por un riel, atraviesa la
barra, y regresa al generador a lo largo del otro riel.
1
(a) Encuentre la velocidad de la barra en función del
tiempo, suponiendo que está en reposo en t=0.
(b)El generador G de corriente constante se reemplaza
por una batería que suministra una fem constante ε.
Demuestre que la velocidad de la barra tiende ahora a un
valor terminal constante v y dé su magnitud y dirección.
¿ Cuál es la corriente en la barra cuando se alcanza esta
velocidad terminal? (c) Analice las situaciones (a) y (b)
desde el punto de vista de las transferencias de energía.
Problema 9: Un alambre rígido doblado en forma de
semicírculo de radio a gira con una frecuencia v dentro
de un campo magnético uniforme. ¿Cuáles son (a) la
frecuencia y (b) la amplitud de la fem inducida en la
espira?
Problema 12: Dos rieles conductores rectos forman un
ángulo θ donde se unen sus extremos. Una barra
conductora en contacto con los rieles y formando un
triángulo isósceles con ellos arranca en el vértice en el
momento t=0 y se mueve a velocidad constante v hacia
la derecha. Un campo magnético B apunta hacia afuera
de la página. (a) Halle la fem inducida en función del
tiempo. (b) Si θ=1100, B= 352 mT y v=5.21 m/s
¿cuándo es la fem inducida igual a 56.8 V?
Problema 10: Una espira rectangular de N vueltas de
longitud a y anchura b gira con una frecuencia v dentro
de un campo magnético uniforme B. (a) Demuestre que
en la espira se genera una fem inducida dada por:
ε = 2πν NabB sen( 2πν t )
Este es el principio del generador comercial de corriente
alterna. (b) Diseñe una espira que produciría una fem de
ε0=150 V al girar a razón de 60 rev/s dentro de un
campo magnético de 0.50 T.
Problema 11: Una barra de longitud L es obligada a
moverse a una velocidad constante v a lo largo de rieles
conductores horizontales. En este caso el campo
magnético en el que se mueve la barra no es uniforme
sino que es provisto por una corriente i en un alambre
paralelo largo. Suponga que v=4.86 m/s, a=10.2 mm,
L=9.83 cm e i=ll0 A. (a) Calcule 1a fem inducida en la
barra. (b)¿Cuál es la corriente en la espira conductora?
Suponga que la resistencia de la barra es de 415 mΩ y
que la resistencia de los rieles es despreciable. (c) ¿Con
qué velocidad se está generando la energía interna en la
barra? (d) ¿Qué fuerza debe aplicarse a la barra por un
agente externo para mantener su movimiento? (e) ¿A
qué velocidad este agente externo realiza trabajo sobre
la barra? Compare esta respuesta con la de (c).
Práctica N012: La ley de inducción de Faraday
Problema 13: Una espira rectangular de alambre con
longitud a, anchura b y resistencia R está situada cerca
de un alambre infinitamente largo que conduce una
corriente i como se muestra en la figura. La distancia
desde el alambre largo a la espira es D. Halle (a) la
magnitud del campo magnético a través de la espira y
(b) la corriente en la espira al moverse alejándose del
alambre con una rapidez v.
Problema 14: Un alambre cuya área de sección
transversal es de 1.2 mm y cuya resistividad es de 1.7 x
10-8 Ωm esta doblado en forma de arco circular de radio
r=24 cm. Un tramo recto adicional de este alambre, OP,
puede girar libremente alrededor del pivote en O y
forma un contacto deslizante con el arco en P. Por
2
último, otro tramo recto de éste alambre, OQ, completa
el circuito. Todo cl sistema está colocado dentro de un
campo magnético B=0.15 T dirigido hacia afuera del
plano del papel. El alambre recto OP parte del reposo a
t=0 y tiene una aceleración angular constante de 12
rad/s. (a) Halle la resistencia de la espira OPQO en
función de θ. (b) Halle el flujo magnético a través de la
espira en función de θ. (c) ¿Para qué valor de θ la
corriente inducida es máxima en la espira? (d) ¿Cuál es
el valor máximo de la corriente inducida en la espira?
Problema 15: La figura muestra dos regiones circulares
R1 y R2 con radios rl=21.2 cm y r2=32.3 cm,
respectivamente. En R existe un campo magnético
uniforme de B1=48 6 mT hacia adentro de la página y en
R2 un campo magnético uniforme de B2=77.2 mT hacia
afuera de la página (haga caso omiso de cualquier efecto
de borde de estos campos). Ambos campos están
decreciendo a razón de 8.50 mT/s. Calcule la integral
∫ Eds para cada una de las tres trayectorias indicadas.
Práctica N012: La ley de inducción de Faraday
3
BUC: Física II.
Práctica N0 13: Inductancia.
Problema 1. La inductancia de una bobina compacta
de 400 vueltas es de 8.0 mH. Calcule el flujo
magnético a través de la bobina cuando la corriente es
de 5.0 mA
Problema 7. Hallar la inductancia del cable coaxial de
la figura. (Sugerencia: calcular el flujo a través de una
superficie rectangular, perpendicular al campo, de
longitud l y ancho b-a.
Problema 2 Se devana un solenoide con una sola capa
de alambre de cobre (diámetro = 2.52 mm) aislado. El
solenoide tiene un diámetro de 4.10 cm y una longitud
de 2.0 m. ¿Cuál es la inductancia por metro del
solenoide cerca de su centro? Suponga que los
alambres contiguos se tocan y que el espesor del
aislamiento es despreciable.
Problema 3 En cierto instante la corriente y la fem
inducida en un inductor son como se indica en la
figura. (a) ¿Está la corriente aumentando o
disminuyendo? (b) La fem es de 17 V, y la velocidad a
la que cambia la corriente es de 25 kA/s; ¿cuál es el
valor de la inductancia?
Problema 8. La corriente en un circuito LR aumenta a
un tercio de su valor de estado estacionario en 5.22 s.
Calcule la constante de tiempo inductiva.
Problema 9 Considere el circuito LR de la figura. En
términos de la fem ε de la batería ¿cual es la fem
inducida cuando el interruptor acaba de cerrarse sobre
a? (b) ¿Cuál es después de dos constantes de tiempo?
(c) Después de esperar a que el sistema llegue al estado
estacionario, el interruptor se cambia de a a b . En ese
instante, ¿cuál es la energía almacenada en el circuito?
¿Cuánta energía se disipa por la resistencia hasta que la
corriente se hace cero?
Problema 4. La inductancia de una bobina de N
vueltas estrechamente devanada es tal que se induce
una fem de 3.0 mV cuando la corriente cambia a razón
de 5.0 A/s. Una corriente estacionaria de 8.0 A
produce un flujo magnético de 40 µWb a través de
cada espira. (a) Calcule la inductancia de la bobina. (b)
¿Cuántas espiras tiene la bobina?
Problema 5. Un toroide de una sección transversal
cuadrada de 5.20 cm y un radio interior de 15.3 cm
tiene 536 vueltas de alambre y conduce una corriente
de 810 mA. Calcule el flujo magnético a través de la
sección transversal.
Problema 6 a) Dos inductores L1 y L2 están
conectados en serie y separados por una distancia
grande. Hallar la inductancia equivalente. (b) lo mismo
cuando están conectados en paralelo y separados por
una gran distancia. (c) ¿Por qué debe ser grande su
separación para que esta relación se cumpla?
Práctica N0 13: Inductancia
Problema 10. En la figura, ε=100V,Rl=10Ω, R2=20Ω
R3=30Ω, y L=2.0 H. Halle los valores de i1 e i2 (a)
inmediatamente después de haber sido cerrado el
interruptor S; (b) un tiempo largo después; (c)
inmediatamente después de que es abierto de nuevo el
interruptor S; (d) un tiempo largo después.
Problema 11. En el circuito que se muestra en la
figura, ε=10V,Rl=5Ω, R2=10Ω y L=5.0 H. Para las dos
condiciones por separado (I) el interruptor S acaba de
cerrarse y (II) el interruptor S ha estado cerrado
durante un tiempo largo, calcule (a) la corriente i1 que
pasa por Rl, (b) la corriente i2 que fluye por R2, (c) la
corriente i en el interruptor, (d) la diferencia de
potencial a través de R2, (e) la diferencia de potencial a
través de L, y (f) di2/dt.
Problema 12. En la figura, el componente de la rama
superior es un fusible ideal de 3.0 A. Tiene una
resistencia nula en tanto que la corriente que pasa por
él permanezca a menos de 3.0 A. Si la corriente
alcanza 3.0 A, se "funde " y después tiene una
resistencia infinita. El interruptor S se cierra en el
tiempo t = 0. (a) ¿Cuando se funde el fusible? (b)
Trace una gráfica de la corriente i que pasa por el
inductor en función del tiempo. Marque el momento en
que se quema el fusible.
corriente en el circuito es cero en el tiempo t=0. (a)
¿En qué tiempo es igual la velocidad a la que se disipa
energía en el resistor a la velocidad a la que la energía
esta almacenándose en el inductor? Suponga que
ε=12.2V, R=7.34Ω, y L=5.48 H. La batería se conecta
en el tiempo t=O. (b)¿Cuánta energía entrega la batería
durante los primeros 2.00 s. (c)¿Cuánta de esta energía
se almacena en el campo magnético del inductor? (d)
¿Cuánta ha aparecido en el resistor?
Problema 15 Un alambre largo conduce una corriente
i distribuida uniformemente en una sección transversal
del alambre. (a) Demuestre que la energía magnética
de un tramo l almacenada dentro del alambre es igual a
µ0i2l/16π (¿Por qué no depende del diámetro del
alambre?) (b) Demuestre que la inductancia en un
tramo l del alambre asociada con el flujo dentro del
alambre es de µ0l/8π.
Problema 16. Considere el circuito mostrado en la
figura. Con el interruptor Sl cerrado y los otros dos
interruptores abiertos, el circuito tiene una constante de
tiempo τc. Con el interruptor S2 cerrado y los otros dos
interruptores abiertos, e1 circuito tiene una constante
de tiempo τL. Con el interruptor S3 cerrado y los otros
dos interruptores abiertos, el circuito oscila con un
período T. Demuestre que
T = 2π τ Cτ L
Problema 13. Un solenoide de 85.3 cm de longitud
tiene un área de su sección transversal de 17.2 cm2.
Hay 950 vueltas de alambre conduciendo una corriente
de 6.57 A. (a) Calcule la densidad de energía del
campo magnético dentro del solenoide. (b) Halle la
energía total almacenada en el campo magnético
dentro del solenoide. (Desprecie los efectos de borde.)
Problema 14. Supóngase que la constante inductiva de
tiempo del circuito de la figura es de 37.5 ms y que la
Práctica N0 13: Inductancia
Problema 17. Un circuito oscilatorio LC que consta de
un capacitor de 1.13 nF y una bobina de 3.17 mH tiene
una caída de potencial pico de 2.87 V. Halle (a) la
carga máxima en el capacitor, (b) la corriente de pico
en el circuito, y (c) la energía almacenada máxima en
el campo magnético de la bobina.
Problema 18. Tres inductores idénticos L y dos
capacitores idénticos C están conectados en un circuito
de dos mallas como se muestra en la figura. (a)
Supóngase que las corrientes sean como se muestran.
¿Cuál es la corriente en el inductor del centro? Escriba
las ecuaciones de la malla y demuestre que se
satisfacen siempre y cuando la corriente oscile con una
frecuencia angular de
ω = 1 / LC
(b) Supóngase ahora que las corrientes son como se
muestra en la figura b. ¿Cual es la corriente en el
inductor del centro? Escriba las ecuaciones de la malla
y demuestre que se satisfacen siempre y cuando la
corriente oscile con una frecuencia angular
ω = 1 / 3LC
Problema 19 Un circuito de una sola malla consta de
un resistor de 7.22 Ω, un inductor de 12.3 H y un
capacitor de 3.18 µF. Inicialmente, el capacitor tiene
una carga de 6.31 µC y la corriente es cero. Calcule la
carga en el capacitor después de N ciclos completos
para N = 5, 10 y 100.
Práctica N0 13: Inductancia
BUC: Física II.
Práctica N 14: Circuitos de corriente alterna.
0
Problema 1. Un inductor de 45.2 mH tiene una
reactancia de 1.28 kΩ (a) Halle la frecuencia. (b) ¿Cuál
es la capacitancia de un capacitor con la misma
reactancia a esa frecuencia? (c) Si la frecuencia se
duplica, ¿cuáles son las reactancias del inductor y del
capacitor?
Problema 2 (a) ¿A qué frecuencia angular tendrían la
misma reactancia un inductor de 6.23 mH y un
capacitor de 11.4 µF? (b) ¿Cuál sería esta reactancia?
(c) Demuestre que esta frecuencia sería igual a la
frecuencia natural de las oscilaciones LC libres.
Problema 5 Considere las curvas de resonancia de la
figura. (a) Demuestre que, para las frecuencias por
arriba de la de resonancia, el circuito es
predominantemente inductivo y que, para las
frecuencias por abajo de la de resonancia, es
predominantemente capacitivo. (b) ¿Cómo se
comporta el circuito en resonancia? (c) Trace un
diagrama de fasores para las condiciones a una
frecuencia más elevada que la de resonancia, en
resonancia, y más baja que la de resonancia.
Problema 3 La salida de un generador de CA es
ε=εmsen (wt), siendo εm=25.0 V y w=377 rad/s. Está
conectada a un inductor de 12.7 H. (a) ¿Cuál es el
valor máximo de la corriente? (b) Cuando la corriente
es un máximo, ¿cuál es la fem del generador? (c)
Cuando la fem del generador es -13.8 V y está
aumentando en magnitud, ¿cuál es la corriente? (d)
Para las condiciones de la parte (c), ¿está el generador
abasteciendo energía o absorbiendo energía del resto
del circuito? (d) Hacer lo mismo cuando el generador
se conecta a un capacitor de 4.15 µF.
Problema 4. La salida de un generador de CA está
dada por ε=εmsen(wt-π/4), en donde εm=31.4 V y
w=350 rad/s. La corriente est dada por
i(t)=imsen(wt-3π/4),
donde im=622 mA. (a) ¿En qué tiempo, después de t=0,
alcanza primero un máximo la fem del generador? (b)
¿En qué tiempo, después de t=0, alcanza primero un
máximo la corriente? (c) El circuito contiene un solo
elemento diferente al generador. ¿Es un capacitor, un
inductor, o un resistor? Justifique su respuesta. (d)
¿Cuál es el valor de la capacitancia, la inductancia, o la
resistencia, según fuera el caso? (e) Repetir el
problema para i(t)=imsen(wt+π/4)
Problema 6 ¿Puede la amplitud del voltaje de un
inductor ser mayor que la fem del generador en un
circuito RLC? Considere un circuito con εm=10.0 V,
R=9.6 Ω, L=1.2 H y C=1.3 µF. Halle la amplitud del
voltaje en el inductor en resonancia.
Problema 7 Una bobina de 88.3 mH de inductancia y
resistencia desconocida y un capacitor de 937 nF están
conectados en serie con un oscilador de 941 Hz de
frecuencia. El ángulo de fase φ entre la fem aplicada y
la corriente es de 75.00. Determine la resistencia de la
bobina.
Problema 8. En cierto circuito RLC la fem máxima
del generador es de 125 V y la corriente máxima es de
3.20 A. Si la corriente se adelanta a la fem del
generador en 56.3o, (a) ¿cuál es la impedancia y (b)
cuál es la resistencia del circuito? (c) ¿Es el circuito
predominantemente capacitivo o inductivo?
Práctica N0 14: Circuitos de corriente alterna
1
Problema 9 Un circuito RLC tiene R = 5.12 Ω,
C=19.3 µF, L=988 mH y εm=31.3 V. (a) ¿A qué
frecuencia angular w tendrá la corriente su valor
máximo? (b) ¿Cuál es este valor máximo? (c) ¿A qué
dos frecuencias angulares w1 y w2 tendrá la amplitud
de la corriente la mitad de este valor máximo? (d)
Halle la anchura fraccionaria [(w1-w2)/w] de la curva
de resonancia.
Problema 10 Demuestre que la potencia promedio
entregada a un circuito RLC puede también escribirse
como
2
P = ε rms
R/Z2
Demuestre que esta expresión da resultados razonables
para un circuito resistivo puro, para un circuito RLC en
resonancia, para un circuito puramente capacitivo, y
para un circuito puramente inductivo.
Problema 11 Consideremos el circuito de antena de
FM que se muestra en la figura, con L=8.22 µH, C=
0.270 pF y R=74.7 Ω. La señal de radio induce en la
antena una fem alterna con εm =9.13 µV. Halle (a) la
frecuencia de las ondas incidentes para las que está
"sintonizada" la antena, (b) la corriente rms en la
antena, y (c) la diferencia de potencial rms en el
capacitor.
Problema 13. El generador de CA de la figura
suministra 170V(max) a 60 Hz. Con el interruptor
abierto como en el diagrama, la corriente resultante se
adelanta a la fem del generador en 20o. Con el
interruptor en la posición 1 la corriente se atrasa de la
fem del generador en 10o. Cuando el interruptor está
en la posición 2 la corriente máxima es de 2.82 A.
Determine los valores de R, L y C.
Problema 14 Un generador suministra 150 V a la
bobina de 65 vueltas del primario de un transformador.
Si la bobina del secundario tiene 780 vueltas, ¿cuál es
el voltaje en el secundario?
Problema 15. Un transformador tiene 500 vueltas en
el primario y 10 vueltas en el secundario. (a) Si Vp en
el primario es de 120 V (rms), ¿cuál es Vs en el
secundario, suponiendo un circuito abierto. (b) Si
ahora se conecta una carga resistiva de 15Ω al
secundario, ¿cuáles son las corrientes en los devanados
del primario y del secundario?
Problema 12 εm En la figura, R =15.0 Ω, C=4.72 µF,
y L=25.3 mH. El generador proporciona un voltaje
senoidal de 75.0 V (rms) a una frecuencia ν=550 Hz.
(a) Calcule la amplitud rms de la corriente. (b) Halle
los voltajes rms Vab, Vbc, Vcd, Vbd, Vad. (c) ¿Qué
potencia promedio se disipa en cada uno de los tres
elementos del circuito?
Práctica N0 14: Circuitos de corriente alterna
Problema 16. Un ingeniero electricista diseña un
transformador ideal para operar una máquina de rayos
X a un potencial pico de 74 kV y una corriente rms de
270 mA. El transformador opera a partir de una fuente
de alimentación de 220 V rms. Sin embargo, no se
tuvo en cuenta la resistencia en los conductores que
unen a esta con el transformador. Al instalarlo, se
comprueba que los conductores de la fuente tienen una
resistencia de 0.62 Ω. ¿En cuánto debe aumentarse el
voltaje de la fuente de alimentación con objeto de
mantener los mismos parámetros operativos en el
transformador?
2
BUC: Física II
Práctica N0 15 Polarización
Problema 1: Cuál es el ángulo de polarización para un haz que incide desde el aire sobre la
superficie del agua (n=1.33)?
Problema 2: Un haz de luz que se refleja en la superficie de un medio transparente queda
completamente polarizado cuando el ángulo de reflexión es 1.1 rad. ¿Cuál es el ángulo de
refracción?
Problema 3: Las ecuaciones de una onda electromagnética en el vacío son:
I) Bx = B0 sen (ky + ωt), By=Bz=0.
II) Bx=0, By = B0 sen (kx - ωt), Bz= B1 cos (kx - ωt)
¿Cuál es la dirección de propagación en cada caso?
¿Está polarizada la onda? De ser así, ¿en qué dirección?.
Problema 4: Sobre dos láminas polarizadoras situadas una encima de la otra cae luz no
polarizada. ¿Cuál debe ser el ángulo entre las direcciones características de las láminas si la
intensidad de la luz transmitida es un tercio de la intensidad del haz incidente? Supóngase que
cada lámina polarizadora es ideal, esto es, que reduce la intensidad de la luz no polarizada al
50% exactamente.
Problema 5: Un haz de luz no polarizada pasa por 3 polarizadores sucesivamente. El primer
polarizador (P1) polariza el haz y los otros dos (P2 y P3) giran el plano de polarización.
Suponer que β es el angulo azimutal entre los polarizadores P1 y P2 y α el angulo azimutal
entre P2 y P3.
Suponiendo que los 3 polarizadores son ideales, demostrar que la intensidad en el detector
colocado despues de P3 es
I= ½ Io cos2 β cos2 α
Notar que el plano de polarización emergente está está girado un
Determinar I cuando α = β = π/4 de tal modo que β +α = π/2.
Práctica N0 15: Polarización
ángulo α + β .
1