CAPÍTULO 2 RESPUESTA EN FRECUENCIA

33
CAPÍTULO 2
RESPUESTA EN FRECUENCIA
2.1. GENERALIDADES.
Introducción.
Para el circuito de la figura 2.1, se encontrarán las funciones circuitales de admitancia
de entrada y de ganancia de voltaje, las cuales se definen como:
Yin( s ) =
I ( s)
Vi( s )
G( s ) =
Vo( s )
Vi( s )
I ( s)
Vi( s )
+
+
−
Vo( s )
−
Figura 2.1
Cualquiera que sea la función circuital, siempre es posible expresarla como el cociente
indicado de dos polinomios racionales enteros, así:
F ( s) =
b0 + b1 s + b2 s 2 +.....+ bm s m
a 0 + a1 s + a 2 s 2 +.....+ a n s n
Cuando la excitación es de tipo senoidal, la frecuencia compleja: s está dada
por: s = jω , siendo: ω la frecuencia de la excitación.
Al reemplazar: s = jω , la función circuital es de variable compleja y se podrá expresar
mediante su parte real y su parte imaginaria, así:
F ( jω ) = R(ω ) + jX (ω )
La función se puede expresar en su forma polar, es decir, mediante su magnitud y su
fase, de la siguiente manera:
F ( jω ) = F ( jω ) e jΘ (ω )
F ( jω ) = R(ω ) 2 + X (ω ) 2
 X (ω )
Θ(ω ) = atan

 R(ω ) 
34
Magnitud de una función circuital en decibelios.
La magnitud en decibelios de una función circuital se define como:
Fdb(ω ) = 20 log F ( jω )
La unidad de decibelios es usada muy a menudo en ingeniería. Con base en lo anterior,
tenemos
F (ω ) = 10 0.05 Fdb
La siguiente tabla ilustra los decibelios asociados a ciertas cantidades.
Cantidad
decibelios
10
3
60
10
2
40
10
1
20
0
0
1
20
2
40
10
3
60
2
3
10
10
10
2.2. DIAGRAMAS DE BODE DE MAGNITUD Y FASE.
Introducción.
El diagrama de Bode de magnitud de una función circuital es una gráfica de la magnitud
en decibelios versus el logaritmo de la frecuencia: log(ω ) .
El diagrama de Bode de fase de una función circuital es una gráfica de la fase versus el
logaritmo de la frecuencia.
Toda función circuital tiene una frecuencia característica: ω p , la cual se toma como
referencia para dibujar los diagramas de Bode.
Para dibujar los diagramas de Bode de magnitud y fase es necesario hacer una partición
del eje de frecuencias en décadas. Una década es el intervalo de frecuencias
comprendido entre dos frecuencias: ω 1 y ω 2 de tal manera que:
ω2
= 10 .
ω1
La figura 2.2. muestra cuatro décadas alrededor de la frecuencia: ω 0
35
0.01ω 0
. ω0
01
ω0
10ω 0
100ω 0
Figura 2.2.
Para ubicar una frecuencia intermedia: ω x en la década comprendida entre una
frecuencia: ω 1 y la frecuencia: 10ω 1 , se procede de la siguiente manera:
ω 
Se calcula la cantidad: d = log x  y se mide la cantidad: d a partir de la
 ω1 
frecuencia: ω 1 .
Por ejemplo, la frecuencia: 38.4 está ubicada en la década: 10……100, a partir de la
. ) , resultando: d = 0.584
frecuencia: 10, se mide la cantidad: d = log(384
Diagramas de Bode de magnitud y fase de una constante.
Dada la función circuital: F ( jω ) = K , la podemos expresar en la forma:
 K e j0
F ( jω ) = 
jπ
K e
K>0
K<0
La magnitud en decibelios es: Fdb(ω ) = 20 log K . El diagrama de Bode de magnitud
consiste de una recta horizontal que puede estar por encima del eje de frecuencias, sobre
el eje de frecuencias o por debajo del mismo, dependiendo de: K .
Si K < 1, la recta está por debajo.
Si K > 1, la recta está por encima.
En cuanto a la fase, el diagrama de Bode correspondiente es una recta horizontal que es
igual a cero si K > 0 y es igual a π si K < 0
Diagramas de Bode de magnitud y fase de un derivador.
Un circuito derivador presenta una función de transferencia de la forma: F ( s ) = s / ω p .
En adelante se hará el siguiente cambio de variable: S = s / ω p , con lo cual, obtenemos
el derivador normalizado: F ( S ) = S si hacemos la sustitución: S = jΩ , se obtiene:
F ( jΩ ) = jΩ = Ωe
j
π
2
La magnitud en decibelios de la función está dada por: Fdb( Ω ) = 20 log(Ω) . El
diagrama de Bode de magnitud es una recta que pasa por la frecuencia característica y
tiene una pendiente de 20 decibelios por década. La figura 2.3. ilustra el diagrama de
Bode de magnitud para un derivador.
En cuanto a la fase, el diagrama de Bode será la recta horizontal: Θ(ω ) =
π
2
36
Diagramas de Bode de magnitud y fase de un circuito integrador.
Un circuito integrador se caracteriza por la función de transferencia:
F ( s) =
ωp
F(S ) =
s
1
S
Puede mostrarse que la magnitud de la función en decibelios está dada por:
ω 
Fdb(ω ) = −20 log 
ωp 
Claramente se observa que el diagrama correspondiente es una recta que pasa por ω p y
tiene una pendiente de menos veinte decibelios por década.
40
20
Fdb(ω )
0
− 20
− 40
0.01ω p
01
. ωp
ωp
10ω p
100ω p
Figura 2.3
Es pertinente anotar que el integrador es el inverso multiplicativo del derivador y, en
consecuencia, el diagrama de Bode del integrador es el inverso aditivo del diagrama de
Bode del derivador. En cuanto a la fase, el diagrama de Bode correspondiente es la recta
horizontal:
Θ(ω ) = −
π
2
La figura 2. 4. muestra el diagrama de Bode de magnitud para el integrador.
Diagrama de Bode de magnitud de una función lineal.
Una función circuital lineal presenta la forma: F ( s ) = 1 +
s
ωp
F ( S ) = 1 + S . Al efectuar
la sustitución: S = jΩ , se obtiene: F ( jΩ ) = 1 + jΩ .
[
La magnitud en decibelios está dada por: Fdb( Ω ) = 10 log 1 + Ω 2
]
37
Para representar el diagrama de Bode correspondiente es necesario dibujar dos asíntotas
y el punto de la gráfica correspondiente a la frecuencia característica, el cual
denominaremos como la corrección.
40
20
Fdb(ω )
0
− 20
− 40
0.01ω p
01
.ωp
ωp
10ω p
100ω p
Figura 2.4
Las asíntotas del diagrama de Bode de magnitud son las rectas que se obtienen para
frecuencias por debajo y por encima de la frecuencia característica, así:
1. Para frecuencias menores que: ω p , obtenemos: Fdb( Ω < 1) = 0
2. Para frecuencias mayores que: ω p , obtenemos: Fdb( Ω > 1) = 20 log(Ω)
3. Para la frecuencia ω p obtenemos: Fdb( Ω = 1) = 3
La figura 2.5. ilustra el diagrama de Bode asintótico de magnitud para la función lineal.
La fase de la función lineal viene dada por: Θ( Ω ) = atan(Ω) .
Para dibujar el diagrama de Bode de fase es necesario trazar tres asíntotas, las cuales se
deducen al analizar la expresión matemática, así:
1. En el intervalo: 0 < ω < 01
. ω p , la fase es prácticamente cero y en consecuencia
obtenemos la asíntota: Θ( Ω ) = 0 .
. ω p < ω < 10ω p , la fase es prácticamente lineal en escala
2. En el intervalo: 01
logarítmica, así:
Θ( Ω ) =
π
4
+
π
4
log(Ω) . Se puede notar que: Θ( 01
. ω p ) = 0 y Θ(10ω p ) =
π
2
3. En el intervalo: ω > 10ω p , la fase es prácticamente de noventa grados, esto es, la
asíntota es la recta horizontal: Θ (Ω ) = π / 2
La figura 2.6 ilustra el diagrama asintótico de fase de la función.
Diagramas de Bode de magnitud y fase para el inverso multiplicativo de una función
lineal.
−1
En este caso la función de transferencia es de la forma: F ( S ) = (1 + S ) .
38
40
20
Fdb(ω )
0
− 20
− 40
0.01ω p
01
.ωp
ωp
10ω p
100ω p
Figura 2.5
π
2
Θ(ω )
π
4
0
0.01ω p
01
. ωp
ωp
10ω p
100ω p
Figura 2.6
El estudiante puede verificar que:
1. Para frecuencias menores que: ω p , obtenemos: Fdb(ω < ω p ) = 0
2. Para frecuencias mayores que: ω p , obtenemos: Fdb(ω > ω p ) = −20 log(Ω)
3. Para la frecuencia: ω p , obtenemos: Fdb(ω = ω p ) = −3
Observe que la figura 2.7. correspondiente es el inverso aditivo del diagrama de Bode
de magnitud de la función lineal. La figura 2.8 muestra el correspondiente diagrama de
Bode asintótico de fase.
39
40
20
Fdb(ω )
0
− 20
− 40
0.01ω p
01
. ωp
ωp
10ω p
100ω p
Figura 2.7
π
2
Θ(ω )
π
4
0
0.01ω p
01
. ωp
ωp
10ω p
100ω p
Figura 2.8
Diagramas de Bode de magnitud y fase para una función cuadrática.
Una función cuadrática presenta la forma:
F ( S ) = 1 + 2 zS + S 2
La cantidad: z es el coeficiente de amortiguamiento y es responsable de la corrección
del diagrama de Bode. Al efectuar la sustitución: S = jΩ , se encuentra que la función
circuital se puede expresar como:
F ( jω ) = 1 − Ω 2 + j(2 zΩ)
Consecuentemente, la magnitud y la fase vienen dadas por:
(
Fdb( Ω ) = 10 log  1 − Ω 2

) + (2 zΩ)
2
2


 2 zΩ 
Θ( Ω ) = atan 
2
1 − Ω 
Al igual que en el caso lineal, el diagrama de Bode de magnitud presenta dos asíntotas y
una corrección a la frecuencia característica, así:
40
1. Para frecuencias menores que: ω p , obtenemos: Fdb(ω < ω p ) = 0
2. Para frecuencias mayores que: ω p , obtenemos: Fdb(ω > ω p ) = 40 log(Ω)
3. Para la frecuencia: ω p , obtenemos: Fdb(ω = ω p ) = 20 log( 2z )
La corrección estará por encima del eje de frecuencias si se verifica que: 2z > 1
La corrección estará por debajo del eje de frecuencias, si se verifica que: 2 z < 1
La figura 2.9 ilustra el diagrama de Bode asintótico de magnitud correspondiente a la
función cuadrática
Para hacer la gráfica corregida a la frecuencia: ω p , es conveniente usar un paquete
graficador. La figura 2.10 ilustra el diagrama de Bode para diferentes valores del
coeficiente de amortiguamiento, usando el paquete MATHCAD.
80
40
Fdb(ω )
0
− 40
− 80
0.01ω p
01
. ωp
ωp
10ω p
100ω p
Figura 2.9
En cuanto al diagrama de Bode de fase, se procede de manera similar a la función lineal.
ω
 2 zΩ 
Si hacemos el cambio de variable: Ω =
, tenemos: Θ( Ω ) = atan

1 − Ω2 
ωp
Primero calculamos las tres asíntotas del diagrama, así:
1. En el intervalo: 0 < ω < 01
. ω p , la asíntota es: Θ( Ω ) = 0
2. En el intervalo: ω > 10ω p , la asíntota es: Θ( Ω ) = π
3. En el intervalo: 01
. ω p < ω < 10ω p , la asíntota es: Θ( Ω ) =
π
+
π
log( Ω )
2 2
En la figura 2.11. se ilustra el diagrama asintótico de fase para la función cuadrática.
Si se observa la expresión para la fase se encuentra una discontinuidad en: Ω = 1, sin
embargo, en escala logarítmica no hay tal discontinuidad según se desprende del
siguiente análisis.
Supongamos que el coeficiente de amortiguamiento es mayor que la unidad, en tal caso,
la función está dada por:
 s 

F ( s) = 1 + 2z
+ 
ω p  ω p 
s
2
41
Figura 2.10
π
Θ(ω )
π
2
0
0.01ω p
01
. ωp
ωp
10ω p
100ω p
Figura 2.11
Si hacemos el cambio de variable: S =
s
ωp
se tiene: F ( S ) = 1 + 2 zS + S 2 .
Si: z ≥ 1 , la función se puede expresar como el producto de dos funciones lineales, así:
S
1
F ( S ) = (1 + aS )(1 + ) . donde: a + = 2z .
a
a
La fase de la función será la suma de las fases individuales, así:
Ω
Θ(Ω) = atan(aΩ) + atan 
a
Se hizo la sustitución: S = jΩ . El valor de a viene dado por: a = z + z 2 − 1 , en
consecuencia, para: z ≥ 1, la expresión matemática para la fase es:
(
)
(
)
Θ(Ω ) = atan z + z 2 − 1 Ω + atan z − z 2 − 1 Ω .
Evidentemente la fase es una función continua para todos los valores de la variable.
42
Teniendo en cuenta la identidad trigonométrica: tan(α + β ) =
tan(α ) + tan( β )
, se
1 − tan(α )tan( β )
puede escribir:
Ω

 aΩ + a 
 2 zΩ 
= atan 
Θ( Ω ) = atan 
2 
2
1 − Ω 
 1− Ω 


Se puede concluir que la expresión de arriba es continua en: Ω = 1, al menos para:
z ≥ 1 . Veremos que si z < 1 , la función deberá ser continua.
Supongamos ahora que el coeficiente de amortiguamiento es menor que la unidad:
z < 1. En este caso podemos expresar la función circuital en la forma:
F ( s ) = 1 + 2 zS + S 2 = 1 + 2 zS + z 2 S 2 + (1 − z 2 )S 2 = (1 + zS ) 2 + (1 − z 2 )S 2
En forma factorizada, queda:
(1 + zS + j 1 − z S )(1 + zS − j 1 − z S )
2
2
Haciendo el cambio de variable: S = jΩ , resulta:
(
)(
F ( jΩ ) = 1 − 1 − z 2 Ω + jzΩ 1 + 1 − z 2 Ω + jzΩ
)
La fase correspondiente viene dada por:




zΩ
zΩ
Θ( Ω ) = atan
 + atan

1− 1− z 2 Ω
1+ 1− z 2 Ω
A partir de la expresión anterior se llega al mismo resultado que se obtuvo para: z > 1 .
Para evitarnos un doble trabajo en la gráfica de la fase, usaremos la siguiente expresión
que es válida para cualquier valor de: z .

 2 zΩ 
Ω ≤1
 atan 1 − Ω 2 


Θ(Ω ) = 
π + atan 2 zΩ  Ω > 1
2

1− Ω 
La figura 2.12 muestra el diagrama corregido de fase para diferentes valores del
coeficiente de amortiguamiento, usando el mismo paquete.
43
Figura 2.12
Diagramas de Bode de magnitud y fase para cualquier función circuital.
De acuerdo con lo estudiado previamente, una función circuital se puede expresar como
el cociente indicado de dos polinomios racionales enteros y cada polinomio se puede
expresar mediante factores lineales y cuadráticos.
Para dibujar el diagrama de Bode de magnitud para una función cualquiera es necesario
expresarla como producto de funciones lineales y cuadráticas de manera tal que el
diagrama definitivo es la suma algebraica de los diagramas individuales.
Para dibujar el diagrama de Bode de fase se procede mediante la suma algebraica de los
diagramas individuales.
Por ejemplo, para la función circuital F(s) dada a continuación, el estudiante puede
verificar que se puede expresar en la forma factorizada indicada a continuación de la
misma.
s
1+
s+ 4
4
F ( s) = 2
F ( s) = 2
2
s + 2s + 2
 s   s 
1+ 2
 +

 2  2
El diagrama de Bode asintótico de magnitud se obtiene como la suma algebraica de los
diagramas de Bode de cada una de las componentes de la función, así:
1. El diagrama de Bode de magnitud del factor constante es la recta horizontal:
20 log( 2)
2. El diagrama de Bode asintótico de magnitud del factor: F1( s ) = 1 + s / 4 está dado por:
ω<4
0

F1db(ω ) = 
20 log(ω / 4) ω > 4
3. El diagrama de Bode asintótico de magnitud del denominador está dado por:

ω < 1/ 2
0
F 2db(ω ) = 
− 40 log( 2ω ) ω > 1 / 2
44
La figura 2.13 ilustra los diagramas de Bode asintóticos de magnitud en los tres casos y
el resultado de sumarlos algebraicamente. Observe la posición relativa de las
frecuencias características: ω 1 = 1 / 2 y ω 2 = 4 .
40
20
Fdb(ω ) 0
− 20
− 40
1 / 10 2
1/ 4
1/ 2
10 / 4
10 / 2
100/4
Figura 2.13
El diagrama de Bode corregido de magnitud se representa usando el MATHCAD y se
muestra en la figura 14. La figura ilustra también los diagramas individuales.
 ω 2  2

 ω 2
2
Fdb(ω ) = 20 log( 2) + 10 log 1 +    − 10 log 1 −
 +ω 
2 


  4  
En cuanto a la fase, tenemos: Θ(ω ) = Θ1 (ω ) − Θ 2 (ω )

 2 zω / 2 

ω≤ 2
 atan
1 − ω 2 / 2 

ω 

Θ1 (ω ) = atan  Θ 2 (ω ) = 
4
π + atan 2 zω / 2  ω > 2
 1−ω2 / 2 




Figura 2.14
z = 2 /2
45
Figura 2.15
Usando el paquete: MATHCAD, representamos el diagrama de Bode de fase de la
función la cual se ilustra en la figura 2.15.
Los diagramas de BODE de magnitud y fase de una función circuital se pueden obtener
con el paquete: MATLAB, usando las siguientes instrucciones:
num = [1,4]
den = [1,2,2]
boden(num, den)
La figura 2.16 ilustra los diagramas de BODE de magnitud y fase para nuestro ejemplo.
El estudiante puede verificar que los resultados son los mismos que se obtienen con
MATHCAD.
Figura 2.16
46
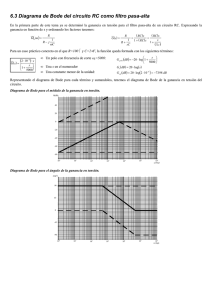
EJERCICIOS 2.2.
1. Un circuito tiene la función de transferencia:
G (s) =
10
s + 2 s + 10
2
a) Dibuje el diagrama de Bode de magnitud.
b) Dibuje el diagrama de Bode de fase.
2. Considere la función de transferencia:
T ( s) =
sm
s 3 + 2s 2 + 2s + 1
Dibuje los diagramas de Bode de magnitud y fase, en los siguientes casos: m = 0,1,2,3,4
3. Dibuje los diagramas de Bode de magnitud y fase para la siguiente función circuital:
G(s) =
( s + 0.69)( s 2 + 0.54s + 1.15)
0.15( s 2 + s + 5.15)
4. Para el circuito de la figura 2.17.
R
R
+
+
V1
C
−
α V2
C
V2
−
Figura 2.17
a. Determine la función de transferencia.
b. Escoja valores para los elementos y dibuje los diagramas de Bode de magnitud y fase
para tres valores diferentes de: α
5. Para el circuito de la figura anterior se coloca una fuente ideal de voltaje a la entrada
y un resistor R a la salida. Repita el procedimiento del ejercicio anterior.
6. La función de atenuación de un circuito está dada por:
A( s) =
5( s 2 + s + 160
. )
2
2( s + 0.2s + 4)
47
a. Dibuje el diagrama de Bode de magnitud.
b. Determine la magnitud de la salida cuando la excitación es:
i) 10 sen( 0.5t )
ii) 10 sen(5t )
7. Para el circuito de la figura 2.18, tome los siguientes datos: R = 1, L = 1 y C = 1 .
V
a. Determine la función de atenuación: A( s) = i
Vo
b. Dibuje el diagrama de Bode de la magnitud.
c. Dibuje el diagrama de Bode de fase.
8. Para el circuito de la figura 2.18, repita el problema anterior si las bobinas están
acopladas y el factor de acople es un medio. Tome los puntos donde desee.
9. En el problema 7, intercambie el resistor de entrada y el capacitor y repita el
procedimiento.
10. En el problema 8, intercambie el resistor de entrada y el capacitor y repita el
procedimiento.
4R
L
C
+
R
Vi (s )
−
L
+
Vo (s )
−
Figura 2.18
2.3. ANÁLISIS FASORIAL.
La sinusoide.
La sinusoide es una combinación lineal de las funciones seno y coseno, así:
f (t ) = C1 cos(ωt ) + C2 sen(ωt )
En la expresión anterior, ω es la frecuencia angular y se mide en radianes/segundo.
Una forma alternativa de expresar la sinusoide es la siguiente:
f (t ) = A cos(ωt − Φ)
48
A es la amplitud de la sinusoide
Φ es la fase, es decir, es el ángulo de desplazamiento de la señal coseno.
Puede verse que:
2
A = C1 + C2
2
Φ = tan −1 (C2 / C1 )
Claramente se observa que la señal senoidal es una función periódica cuyo periodo
2π
y se mide en segundos.
viene dado por: T =
ω
2π
ωt
π /4
Figura 2.19
2π
−π /4
ωt
Figura 2.20
La figura 2.19 muestra la gráfica de la sinusoide: x(t ) = A cos(ωt − π / 4) , mientras que
la figura 2.20 ilustra la gráfica de la sinusoide: y (t ) = A cos(ωt + π / 4) . Obsérvese que
en ambos casos el eje horizontal es el ángulo: ωt
Sinusoides desfasadas.
Consideremos dos sinusoides de la misma frecuencia pero con fases diferentes, así:
x1 (t ) = A1 cos(ωt − Φ1 ) x2 (t ) = A2 cos(ωt − Φ 2 )
El ángulo de desfase viene dada por: ∆Φ = Φ 2 − Φ1 . Se dice que la sinusoide x1 (t ) está
en adelanto con respecto a la otra sí el ángulo de desfase es positivo, es decir la primera
sinusoide alcanza el valor máximo primero que la otra. La sinusoide sólida de la figura
2.21 está en adelanto con respecto a la punteada.
49
∆Φ
Figura 2.21
Valor efectivo de una sinusoide.
El valor efectivo o valor rms de una función periódica de periodo T se define como:
f rms =
1 t 0 +T 2
f (t )dt
T ∫t 0
A
2
Para la sinusoide : f (t ) = A cos(ωt − Φ) , el valor efectivo viene dada por: f rms =
Circuitos de corriente alterna
Consideremos un circuito pasivo RLC, inicialmente en reposo tal como lo muestra la
figura 2.22.
De acuerdo con lo estudiado hasta el momento, la respuesta y (t ) del circuito está
relacionada con la excitación mediante una ecuación diferencial lineal de coeficientes
constantes, así:
(a D
n
n
)
(
)
+ an −1D n −1 + ... + a2 D 2 + a1D + a0 y (t ) = bm D m + bm −1D m −1 + b2 D 2 + b1D + b0 e(t )
e(t )
+
−
+
RLC
y (t )
−
Figura 2.22
Definimos los operadores:
P( D) = an D n + an −1D n −1 + ... + a2 D 2 + a1D + a0
Q( D) = bm D m + m −1 D m −1 + ... + b2 D 2 + b1D + b0
En tal caso podemos escribir la ecuación diferencial de una manera más concisa, así:
P( D) y (t ) = f (t ) = Q( D)e(t )
50
El término independiente f (t ) de la ecuación diferencial depende de la excitación. La
solución general de la ecuación diferencial presenta dos partes, así:
y (t ) = yc (t ) + yss (t )
La primera parte de la solución se conoce como solución complementaria o respuesta
transitoria del circuito y es una combinación lineal de soluciones linealmente
independientes de la homogénea asociada, así:
yc (t ) = C1 y1 (t ) + C2 y2 (t ) + ... + Cn yn (t )
La solución complementaria se determina resolviendo la ecuación característica:
L (λ ) = 0 .
La segunda parte se conoce como respuesta forzada o respuesta de estado estacionario o
respuesta de régimen permanente y depende de la excitación. En principio se determina
por el método del operador inverso, así:
1
yss (t ) =
f (t )
L( D)
Las técnicas de solución en el dominio de tiempo serán reemplazadas por técnicas en el
dominio de la frecuencia, es decir, usando la transformada de Laplace. Recordemos
brevemente las fórmulas de transformación.
Consideremos un circuito RLC serie como lo ilustra la figura 2.23. La ley de Kirchhoff
para voltajes establece que:
vR (t ) + vL (t ) + vC (t ) = vi (t )
L
R
Ls
R
I ( s)
i (t )
vi (t )
C
Vi (s )
Figura 2.23
1
Cs
Figura 2.24
Con base en los principios circuitales, tenemos:
vR (t ) = Ri (t )
vL (t ) = L
d
i (t )
dt
vC (t ) =
1 t
1 t
i(t )dt = vC (0− ) + ∫ i(t )dt
∫
C −∞
C 0
Suponiendo que el sistema está inicialmente en reposo y aplicando la transformada de
Laplace, tenemos:
VR ( s) + VL ( s) + VC ( s) = Vi ( s)
51
A partir de las relaciones entre la corriente y el voltaje en los elementos, se tiene:
VR ( s ) = RI ( s )
VL ( s ) = LsI ( s )
VC ( s) =
1
I ( s)
Cs
El circuito de la figura 2.24 es el equivalente, en el dominio de la frecuencia, del
circuito de la figura 2.23.
Impedancia de un elemento circuital
La relación entre el voltaje y la corriente en un elemento en el dominio de la frecuencia
recibe el nombre de impedancia del elemento.
Puede verse que:
a. La impedancia del resistor es Z R ( s ) = R , es decir, la impedancia de un resistor es
constante e igual a su resistencia.
b. La impedancia del inductor es Z L ( s ) = Ls , es decir, la impedancia de un inductor es
directamente proporcional a la frecuencia.
c. La impedancia del capacitor es Z C ( s) = 1 / Cs , es decir, la impedancia de capacitor es
inversamente proporcional a la frecuencia.
Admitancia de un elemento circuital
Es la relación entre la corriente y el voltaje en el dominio de la frecuencia, es decir, la
admitancia es el inverso de la impedancia. Evidentemente, las admitancias de los tres
elementos circuitales básicos son:
a. . Para el resistor: YR ( s ) = 1 / R
b. Para el inductor: YL ( s ) = 1 / Ls
c. Para el capacitor: YC ( s) = Cs
Técnicas de simplificación de circuitos
Elementos en serie
Dos elementos circuitales con impedancias individuales: Z1( s) y Z 2( s) conectados en
serie, se pueden tratar, para efectos de análisis, como un solo elemento cuya impedancia
equivalente es la suma de las impedancias individuales, así:
Ze( s) = Z1( s ) + Z 2( s )
Elementos en paralelo
Dos elementos circuitales con admitancias individuales: Y 1( s) y Y 2( s) conectados en
paralelo, se pueden tratar, para efectos de análisis, como un solo elemento cuya
admitancia equivalente es la suma de las admitancias individuales, así:
Ye( s ) = Y1( s) + Y 2( s)
52
Transformación de fuentes reales
Para efectos de análisis, una fuente real de voltaje: Ve (s ) en serie con una
impedancia: Z ( s) es equivalente a una fuente real de corriente: I e (s ) en paralelo con la
impedancia: Z (s). La equivalencia de las fuentes implica que:
Ve ( s ) = Z ( s) I e ( s)
Equivalente Thévenin
a
Z e (s )
a
Ve (s )
b
+
−
b
Figura 2.25
Figura 2.26
El sistema de la figura 2.25 es un circuito cualquiera y se tiene acceso a los terminales
a y b . El circuito de la figura 2.26 es el equivalente Thévenin entre a y b si se verifica
que
1) Ve (s) es el voltaje de circuito abierto entre los terminales dados.
2) Z e (s ) es el cociente entre el voltaje de circuito abierto y la corriente de
cortocircuito.
Para encontrar el equivalente Thévenin entre dos puntos dados de un circuito se procede
de la misma forma que si fueran circuitos resistivos, es decir, haciendo las dos pruebas o
aplicando las técnicas de simplificación.
Análisis de circuitos en el dominio de la frecuencia.
Un circuito en el dominio de la frecuencia se puede analizar por el método de las
corrientes de malla o por el método de los voltajes de nodos, de la misma forma que
para circuitos resistivos.
Para el sistema de la figura 2.27, al transformar la ecuación diferencial resulta:
(a s
n
n
)
(
)
+ an −1s n −1 + ... + a2 s 2 + a1s + a0 Y ( s) = bm s m + bm −1s m −1 + ... + b2 s 2 + b1s + b0 E ( s)
La salida del circuito se puede expresar en la forma:
Y (s) =
bm s n + bm −1s n −1 + ... + b2 s 2 + b1s + b0
E ( s)
an s n + an −1s n −1 + ... + a2 s 2 + a1s + a0
Se define la función de transferencia del circuito como el cociente entre la salida y la
entrada en el dominio de la frecuencia, así:
53
H (s) =
n −1
bm s + bm −1s + ... + b2 s + b1s + b0
an s n + an −1s n −1 + ... + a2 s 2 + a1s + a0
n
2
m≤n
En el dominio de tiempo, la salida es la transformada inversa, así:
y (t ) = L−1{Y ( s)} = L−1{H ( s) E ( s)}
Circuitos con excitación sinusoidal.
Cuando la excitación e(t ) circuito de la figura 2.22 es una sinusoide de la forma:
e(t ) = A cos(ωt ) , la transformada de Laplace viene dada por:
E (s) =
As
s +ω2
2
En tal caso la salida es:
 Q( s) As 
y (t ) = L−1{Y ( s)} = L−1 
2
2
 P( s) s + ω 
Suponiendo que P(s) no tiene factores de la forma s 2 + ω 2 , la descomposición en
fracciones parciales de Y (s ) tendrá dos términos correspondientes a la respuesta de
estado estacionario, así:
yss (t ) = a1 (ω ) cos(ωt ) + a2 (ω ) sen(ωt )
Es claro que los coeficientes dependen de la frecuencia y que la respuesta de estado
estacionario se puede expresar en la forma:
yss (t ) = C (ω ) cos[ωt − Φ (ω )]
Se concluye que si la excitación es una sinusoide de frecuencia ω entonces la respuesta
de estado estable es otra sinusoide de la misma frecuencia con amplitud y fase
dependientes de la frecuencia.
En lo que sigue nos interesará únicamente la respuesta de estado estacionario ante
excitaciones de tipo sinusoidal.
Ejemplo 3.1.
Consideremos el circuito de la figura 2.27.
a. Determine el voltaje en el resistor en el dominio de la frecuencia.
b. Asigne valores a los parámetros y determine la respuesta ante la señal:
e(t ) = 10 cos(4t )
54
L
C
+
i (t )
R
e(t )
v(t )
−
Figura 2.27
Solución.
a. Al aplicar la Ley de Kirchhoff para voltajes en el dominio de la frecuencia, resulta:
R
s
L
V (s) =
E (s)
R
1
2
s + s+
L
LC
b. Tomando los datos: R = 2Ω L = 1H
V (s) =
C = 0.1F , se tiene:
2s
20 s 2
=
E
(
s
)
s 2 + 2 s + 10
( s 2 + 2 s + 10)( s 2 + 16)
Descomponiendo en fracciones parciales se tiene:
Y ( s) = −
4 8s + 15
32 s + 3
+
2
5 s + 2 s + 10 5 s 2 + 16
La respuesta de estado estacionario es la inversa de Laplace de segundo término de la
derecha, es decir:
32
24
 32 s + 3 
yss (t ) = L−1 
cos(4t ) +
sen(4t )
 ⇒ yss (t ) =
2
5
5
 5 s + 16 
La respuesta de estado estacionario se puede escribir como:
(
yss (t ) = 8 cos 4t − tan −1 (3 / 4)
)
La excitación exponencial compleja.
Hemos encontrado que sí la excitación de un circuito es: e(t ) = E cos(ωt ) , la respuesta
es una sinusoide de la misma frecuencia pero cuya amplitud y fase dependen de la
frecuencia.
Se sabe que la función coseno es la parte real de una función exponencial compleja, esto
es:
55
cos(ωt ) = Re[e
jωt
]
Consecuentemente la salida será la parte de real de la correspondiente función
exponencial compleja, es decir:
y (t ) = Re[C(ω )e jωt ]
En la expresión anterior se tiene que: C(ω ) = C(ω ) e jΦ (ω ) , es decir es un número
complejo con magnitud y fase dependientes de la frecuencia. Usualmente se utiliza la
siguiente simbología para el número complejo: C(ω ) = C(ω ) e jΦ (ω ) = C(ω ) ∠Φ (ω ) .
Dicho número complejo recibe el nombre de fasor. Los fasores tiene un tratamiento
similar al de los vectores.
Claramente se observa que la magnitud de la salida está relacionada con la función de
transferencia tal como se indica en la figura 2.28.
Ejemplo 2.2.
Usando la técnica fasorial verifique el resultado del ejemplo anterior.
Solución.
Reescribimos el circuito de la manera ilustrada en la figura 2.29. Teniendo en cuenta
que:
1
5
= −j
ZR = 2
ω = 4 Z L = jωL = j 4 Z C =
jωC
2
E H ( jω ) cos(ωt + Φ (ω ))
E cos(ωt )
H ( jω ) = H ( jω ) e
jΦ (ω )
Figura 2.28
− j5 / 2
j4
10∠0
I
ω =4
Figura 2.29
Aplicando el divisor de voltajes se tiene:
2
+
V
−
56
V=
2
40
10 =
= 8∠ − tan −1 (3 / 4)
2 + j 4 − j5 / 2
4 + j3
De acuerdo con lo estudiado se tiene que: v(t ) = 8 cos(4t − 0.644) . Como puede verse,
el resultado es idéntico al encontrado previamente. A partir del resultado puede verse
que el voltaje de salida está atrasado con respecto al voltaje de entrada un ángulo de
0.644 Radianes, equivalente a 36.9o .
La figura 2.30 muestra las formas de onda tanto del voltaje de entrada como del de
salida. Por otro lado, la figura 1.13 ilustra el diagrama fasorial correspondiente.
La ventaja de los diagramas fasoriales estriba en la facilidad para sumar y multiplicar
por escalares, tal como se hace con los vectores. Puede verse que la técnica desarrollada
reduce el análisis al manejo de la aritmética de los números complejos.
4t
Figura 2.30
10∠0
Φ = −36.9
o
8∠ − 36.9o
Figura 2.31
Ejemplo 2.3.
a. Determine el equivalente Thévenin entre los puntos a y b para el circuito de la figura
2.32
b. Determine el voltaje en una carga de 2 Ohmios conectada entre dichos puntos.
Solución.
a. para hallar el equivalente Thévenin se transforman las fuentes de voltaje a fuentes de
corriente, tal como se muestra en la figura 2.33.
12∠0 24 + j12
=
, mientras que la
La corriente I de la figura 2.33 viene dada por: I =
2 − j1
5
impedancia asociada es: Z = 2 − j1 .
57
− j1Ω
2Ω
12∠0
ω =2
a
j 2Ω
1Ω
2∠0
4∠0
ω =2
ω =2
b
Figura 2.32
j 2Ω
I∠Θ
2∠0
Z
1Ω
4∠0
Figura 2.33
Al simplificar el circuito se tiene:
I Equiv =
24 + j12
34 + j12
−2+4 =
5
5
Por otro lado, la impedancia equivalente es:
Z Equiv =
1
1
+1
2 − j1
=
2 − j1 7 − j1
=
3 − j1
10
Finalmente, el voltaje Thévenin viene dado por:
VTh =
34 + j12 7 − j1
⋅
= 5 + j1 = 26∠ tan −1 (1 / 5)
5
10
La impedancia Thévenin viene dada por:
ZTh =
7 − j1
7 + j19
+ j2 =
10
10
58
b. Al colocar una carga de 2Ω , el voltaje en la carga es:
VL =
2
20(5 + j1) 20(5 + j1)(27 − j19) 308 − j136
=
⋅ (5 + j1) =
=
7 + j19
27
j
19
1090
109
+
2+
10
El voltaje en la carga se puede expresar como:
VL = 3.0889∠ tan −1 (−136 / 308) = 3.081531∠ − 23.82o
Así las cosas, sí la frecuencia es: ω = 2 , el voltaje en la carga es:
vL (t ) = 3.0889 cos(2t − 0.4158)
Ejemplo 2.4.
Para el circuito de la figura 2.34, determine el voltaje en el resistor de 2Ω que está en
serie con el inductor usando la técnica de las corrientes de malla.
2Ω
12∠0
ω =2
j 2Ω
− j1Ω
I1
2∠0
1Ω
I2
I3
4∠0
2Ω
Figura 2.34
Solución.
Del circuito se desprende que: I1 − I 2 = 2
Al recorrer la súper malla de la izquierda se tiene: − 12 + (2 − j1) I1 + 1( I 2 − I 3 ) + 4 = 0
Al recorrer la malla de la derecha resulta: − 4 + 1( I 3 − I 2 ) + (2 + j 2) I 3 = 0
El sistema organizado en forma matricial es el siguiente:
−1
0   I1  2
 1
2 − j1 1
− 1   I 2  = 8 

 0
− 1 3 + j 2  I 3  4
59
380 + j104
109
162 + j104
Al resolver el sistema resulta: I 2 =
109
154 − j 68
I3 =
109
I1 =
308 − j136
. Comparando con el
109
ejemplo anterior se observa que los resultados son idénticos.
En consecuencia, el voltaje pedido es: VL = 2 I 3 =
La rutina en Matlab para resolver el sistema e:
Se definen las matrices A y b
La solución es: inv(A)*b
Potencia en estado estable.
Consideremos una combinación de elementos pasivos en el dominio de tiempo, tal
como lo muestra la figura 2.35.
+
v(t )
−
i(t )
Figura 2.35
La potencia instantánea absorbida por la combinación de elementos pasivos viene dada
por:
p (t ) = v(t )i (t )
Cuando las variables circuitales son sinusoides, la potencia instantánea es otra sinusoide
de frecuencia 2ω , tal como se demuestra a continuación.
Supongamos que las señales de corriente y voltaje son las siguientes:
v(t ) = Vm cos(ωt ) i (t ) = I m cos(ωt + Φ )
La potencia instantánea es:
p (t ) = Vm I m cos(ωt ) cos(ωt + Φ )
Haciendo uso de la identidad trigonométrica: 2 cos(a) cos(b) = cos(a + b) + cos(a − b)
se puede escribir:
1
p (t ) = Vm I m {cos(2ωt + Φ ) + cos(Φ )}
2
60
La potencia promedio.
1 T
p (t )dt .
T ∫0
Con base en lo anterior, la potencia promedio para el caso senoidal viene dada por:
La potencia promedio de una señal de periodo T se define como: P =
1
P = Vm I m cos(Φ )
2
Obsérvese que la potencia siempre es positiva independientemente de si el ángulo de
desfase entre el voltaje y la corriente sea negativo o positivo ya que la función coseno es
par.
Ahora bien, dado que el valor efectivo de una sinusoide es el cociente entre el valor
V
I
máximo y 2 , es decir: VE = m I E = m , se tiene: P = VE I E cos(Φ ) .
2
2
En la práctica, para calcular la potencia promedio o potencia activa se determinan los
fasores de corriente y voltaje, así:
Fasor de voltaje: V = Vm ∠Φ1
Fasor de corriente: I = I m ∠Φ 2
1
Potencia activa: P = Vm I m cos(Φ 2 − Φ1 )
2
+
Vm ∠Φ1
−
Z ( jω )
I m ∠Φ 2
Figura 2.36
Factor de potencia.
Un concepto de fundamental importancia en el análisis de circuitos es el de factor de
potencia. Con base en el circuito de la figura 2.36, se tiene que la impedancia viene
dada por:
V V
Z = = m ∠Φ1 − Φ 2
I
Im
El factor de potencia es un número adimensional definido como:
pf = cos(Φ1 − Φ 2 )
Se dice que el factor de potencia es en atraso si Φ1 − Φ 2 > 0 , es decir, si la combinación
de elementos es de tipo inductivo. En caso contrario el factor de potencia es en adelanto.
61
Potencia compleja.
Para el circuito de la figura 2.36, la potencia compleja en la combinación de elementos
1
mostrada se define como: S = VI∗ , dónde I ∗ es el conjugado del fasor de corriente.
2
De hecho, la potencia compleja se puede expresar en la forma:
1
1
S = P + jQ = Vm I m cos(Φ1 − Φ 2 ) + j Vm I m sen(Φ1 − Φ 2 )
2
2
Haciendo Uso de los valores efectivos de voltaje y corriente, se tiene:
S = P + jQ = VE I E cos(Φ1 − Φ 2 ) + jVE I E sen(Φ1 − Φ 2 )
La magnitud de la potencia compleja recibe el nombre de potencia aparente y se mide
en volta-amperios.
La parte real de la potencia compleja es la potencia activa y se mide en vatios
La parte imaginaria de la potencia compleja es la potencia reactiva y se mide en voltaamperios reactivos.
Ejemplo 2.5.
Una fuente de 110 Voltios rms se conecta a una carga capacitiva dada por: Z = 10 − j 2 .
Determine la corriente, la potencia compleja, la potencia aparente, la potencia activa, la
potencia reactiva y el factor de potencia.
Solución.
El fasor de voltaje es: V = 110 2∠0 . Por tanto, el fasor de corriente es:
I=
110 2∠0 110 2 (10 + j 2) 110 2
=
=
∠ tan −1 (0.2)
10 − j 2
124
124
La potencia compleja es: S = 110 2 ⋅
110 2
∠ − tan −1 (0.2)
124
En consecuencia se tiene:
1
(110) 2
VA
Potencia aparente: S = Vm I m =
2
124
El factor de potencia es: pf = cos(tan −1 (−0.2)) =
10
≅ 0.898 en adelanto
124
10 ⋅ (110) 2
Vatios
124
2 ⋅ (110) 2
2
La potencia reactiva es: Q = S ⋅ 1 − pf =
124
La potencia activa es: P = S ⋅ pf =
62
EJERCICIOS 2.3.
1. Para el circuito de la figura 2.37.
a. Usando la técnica de las corrientes de malla determine el voltaje de salida v0 (t )
b. Usando la técnica de los voltajes de nodo determine el voltaje de salida v0 (t )
+ v0 (t ) −
2Ω
10∠0
j 3Ω
4Ω
− j 2Ω
2∠0
ω =4
2Ω
5∠0
Figura 2.37
+ Vx −
5 KΩ
5 KΩ
− j 5KΩ
1∠0
ω = 120π
4 ⋅ 10−4Vx
6 KΩ
j 2 KΩ
12 KΩ
Figura 2.38
2. Para el circuito de la figura 2.38
a. Usando la técnica de las corrientes de malla determine el voltaje de salida v0 (t )
b. Usando la técnica de los voltajes de nodo determine el voltaje de salida v0 (t )
3. Para el circuito de la figura 2.39 se tienen los siguientes datos y determine el voltaje
de salida.
R = 5Ω C = 0.1F L = 1H vi (t ) = 10 cos(2t )
63
R
L
L
R
+
C
vi (t )
vo (t )
R
−
C
Figura 2.39
4. Repita el problema anterior para el circuito de la figura2.40. Tome α = 3
R
R
C
R
+
vi (t )
C
αv0 (t )
vo (t )
−
Figura 2.40
5. Para los circuitos de las figuras 2.39 y 2.40 calcule la potencia activa en la fuente
independiente y el correspondiente factor de potencia.
C