Tablas Z

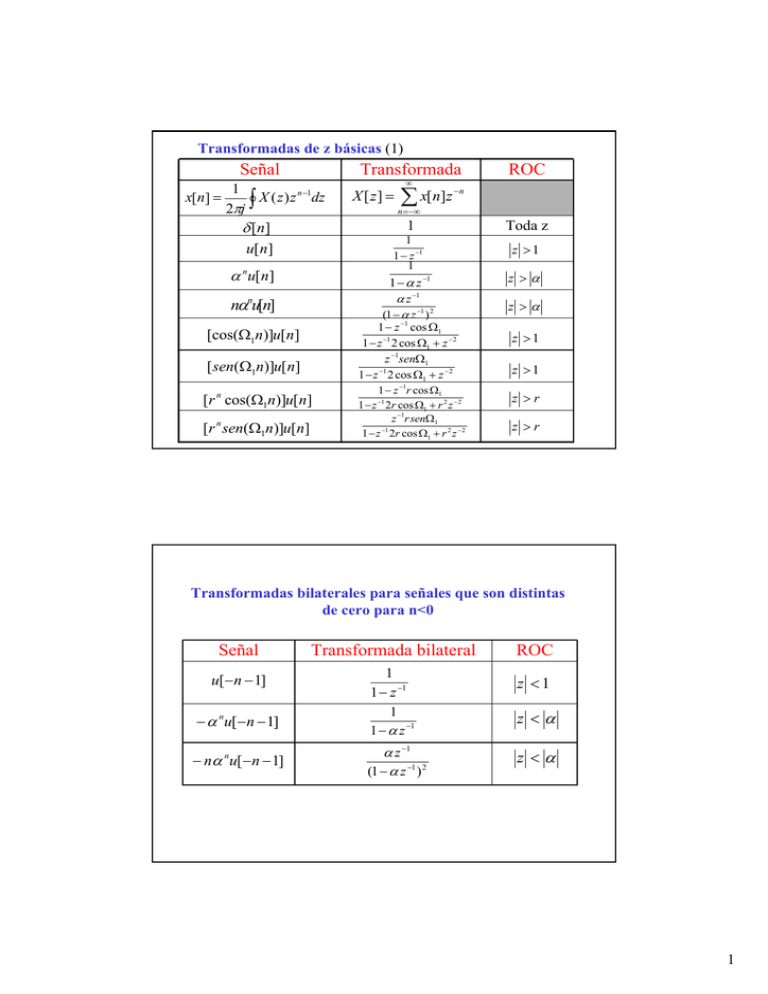
Transformadas de z básicas (1)
Señal
Transformada
1
x[n] =
X ( z ) z n −1dz
∫
2πj
δ [n]
u[n]
∑ x[n]z
nαnu[n]
n = −∞
1
Toda z
1
1 − z −1
z >1
1 − z −1 cos Ω1
1 − z −1 2 cos Ω1 + z − 2
z −1senΩ1
1 − z −1 2 cos Ω1 + z − 2
[cos(Ω1n)]u[n]
[ sen(Ω1n)]u[n]
[r n cos(Ω1n)]u[n]
ROC
−n
1
1 − α z −1
α z −1
(1 − α z −1 ) 2
α nu[n]
[r n sen(Ω1n)]u[n]
X [ z] =
∞
−1
1 − z r cos Ω1
1 − z −1 2r cos Ω1 + r 2 z − 2
z −1r senΩ1
−1
1 − z 2r cos Ω1 + r 2 z − 2
z >α
z >α
z >1
z >1
z >r
z >r
Transformadas bilaterales para señales que son distintas
de cero para n<0
Señal
Transformada bilateral
u[−n − 1]
1
1 − z −1
1
1 − α z −1
− α nu[− n − 1]
− nα nu[− n − 1]
α z −1
(1 − α z −1 ) 2
ROC
z <1
z <α
z <α
1
Propiedades de la transformada z
Señal
x[n]
y[n]
Transformada Transformada
unilateral
bilateral
X(z)
X(z)
ROC
Rx
Ry
Y(z)
Y(z)
al menos Rx ∩ R y
aX(z)+bY(z) aX(z)+bY(z)
−k
x[n-k]
z X (z )
Rx excepto posibl.para |z|=0,inf.
vea abajo
n
α x[n]
|α|Rx
X(z/α)
X(z/α)
x[-n]
X(1/z)
no
1/ Rx
x[n]*y[n]
al menos Rx ∩ R y
X(z)Y(z)
X(z)Y(z)
ax[n]+by[n]
nx[n]
−z
d
X (z )
dz
−z
d
X (z )
dz
Rx excepto posibl. En la suma o
eliminación de z=0
Propiedades de corrimiento en el tiempo de la transformada z unilateral
zu
x[n − k ] ←⎯→
x[−k ] + x[− k + 1]z −1 + L + x[−1]z − k +1 + z − k X(z) , ∀k > 0
zu
x[n − k ] ←⎯→
− x[0]z k − x[1]z k −1 − L − x[k − 1]z + z k X(z) , ∀k > 0
2