pdf-explicacion-para-resolver-fracciones-parciales-con-polos-complejos

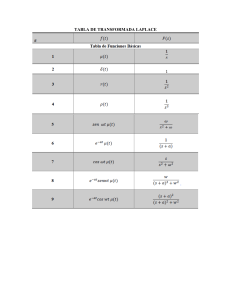
Explicación para resolver fracciones parciales con polos complejos (Taller):
El determinante de A es igual a:
-4s5-24s4-18s3-4s2
O lo que es lo mismo s2(-4s3-24s2 -18s-4)
La factorización del polinomio de grado tres resulta:
S1=- 0.4167692 + 0.1409238i
S2= - 0.4167692 - 0.1409238i
S3= - 5.1664616
Por lo que tenemos dos raíces iguales a cero, y el polinomio de grado 3 al factorizar, da como
resultado raíces complejas, eso se puede resolver de la siguiente manera:
Suponiendo que les queda:
𝑃𝑎𝑟𝑎
𝑞1 (𝑠) =
𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑛𝑡𝑒 𝑑𝑒 𝑞1(𝑠)
𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑛𝑡𝑒 𝑑𝑒 𝑞1(𝑠)
= 2
𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑛𝑡𝑒 𝑑𝑒 𝐴
𝑠 (−4𝑠3 − 24𝑠2 − 18𝑠 − 4)
𝐴 𝐵
𝐶
𝐷
𝐷*
+
+
= + 2+
𝑠 𝑠
(𝑠 + 5.17) (𝑠 + 0.42 − j014) (𝑠 + 0.42 + j0.14)
Se tiene que linealizar normalmente y hallan A,B,C y D y D*, luego la transformada inversa del
𝐴
𝐵
𝐶
primer ( 𝑠 ) , segundo término (𝑠2) y tercer término
(𝑠+5.17)
se hallan fácilmente (sin importar que
las constantes A, B y C sean números complejos, puesto que igual son constantes y salen de la
transformada), lo nuevo es hallar el cuarto y quinto termino, pero esos dos elementos, forman un
solo resultado de transformada inversa, cuya ecuación es la siguiente:
Para (
𝐷
(𝑠+0.42−j014)
+
𝐷*
)
se obtiene, como transformada inversa:
(𝑠+0.42+j0.14)
𝑓(𝑡) = 2|𝐷|𝑒−σ𝑡cos(𝜔𝑡 + 𝜑)
En donde |𝐷| es el modulo de ese número; pudiendo ser D un número real o un número complejo.
σ es el valor real del numero complejo que les dio en el denominador, ω es el número imaginario
𝑝𝑎𝑟𝑡𝑒 𝑖𝑚𝑎g𝑖𝑛𝑎𝑟𝑖𝑎
(sin la j) y 𝜑 = 𝑎𝑟𝑐𝑡𝑎𝑛𝑔 (
Por lo que para
𝑝𝑎𝑟𝑡𝑒 𝑟𝑒𝑎𝑙
) del denominador.
𝐴
𝐵
𝐶
𝑞1(𝑡) = ℒ−1 ( ) + ℒ−1 ( ) + ℒ−1 (
)
𝑠
𝑠2
(𝑠 + 5.17)
𝐷*
𝐷
+ ℒ−1 (
)
+
(𝑠 + 0.42 − j0.14) (𝑠 + 0.42 + j0.14)
𝑓(𝑡) = 2|𝐷|𝑒−σ𝑡cos(𝜔𝑡 + 𝜑)