Aplicaciones de la Integral

203
CAPÍTULO VIII
APLICACIONES DE LA INTEGRAL
8.1 VOLÚMENES DE SÓLIDOS DE REVOLUCIÓN
Cuando una región plana es girada alrededor de un eje de revolución engendra
un sólido de revolución.
y
y
x
x
La primera región resulta de girar una región parabólica alrededor del eje y,
mientras que en el segundo caso se ha girado un rectángulo alrededor del eje
constituido por la parte superior del rectángulo.
8.1.2 METODO DE LOS DISCOS
w
R
r
eje de
revolución
El volumen generado al girar el rectángulo en torno al eje de revolución genera
un disco cuyo volumen es:
Volumen disco
(R2
r 2 )w
Si en lugar de girar un rectángulo se gira el área de la siguiente figura tenemos:
204
x
R(x)
r(x)
x=a
x=b
Cada disco representativo del volumen viene dado por:
( R( x) 2
V
r ( x) 2 ) x
Se puede obtener una aproximación del volumen, calculando el volumen de n
discos similares de ancho x.
n
R ( xi ) 2
VolSólido
r ( xi ) 2 x
i 1
n
R ( xi ) 2 r ( x i ) 2 x
VolSólido lim
n
i 1
El volumen exacto para eje de revolución horizontal será:
b
R( x ) 2
VolSólido
r ( x ) 2 dx
a
Si el eje de revolución es vertical se tendrá:
b
R( x ) 2
VolSólido
r ( x ) 2 dy
a
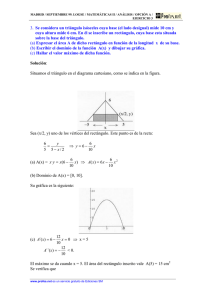
Ejemplo 1 Calcular el volumen del sólido engendrado al girar la región
acotada por
205
y = x ; y = 0 ; x = 4 por revolución en torno de: a) el eje x b) el eje y c) la
recta x = 4 d) la recta x = 6.1
y
y= x
dx
4
x
a) eje x
b
A
4
R
2
2
r dx
x
a
0 2 dx
0
4
A
2
x2
2
x dx
0
4
42
2
0
0
8
b) eje y
d
2
A
R
2
2
c
x
42
r dy
0
2
y2
A
2
4
2
4
y dy
16 y
0
dy
25
5
A
16 * 2
A
160 37
5
4
2
y 2 dy
32
y5
5
2
0
325
5
128
5
1 LARSON HOSTETLER, Cálculo y Geometría Analítica Mc Graw Hill, 1986 Pag 287
206
c) x=4
y2
4
2
dy
4
d
2
A
R
2
2
r dy
c
2
A
A
2
0 2 dy
0
(4
y
2
2 2
16 8 y 2
0)dy
0
A
y2
4
0
y3
16 y 8
3
32
y 4 dy
64
3
32
5
y5
5
2
16 * 2 8
0
23
3
25
5
480 320 96
15
256
15
d)
6
y2
2
dy
4
x=6
207
d
2
R2
A
r 2 dy
c
2
2
y4
y 4 12 y 2
4 dy
0
A
32 dy
0
5
A
22 dy
0
36 12 y 2
A
y 2 )2
(6
y
5
2
3
12
y
3
32
32
5
5
2
5
32 y
0
32 160
5
4
23
1
64
192
5
8.2.2 MÉTODO DE LAS CAPAS
El volumen de una capa cilíndrica generada por un rectángulo es igual a:
h
h
w
p
p
eje de revolución
Vol
w
2
p
2
Vol
p
Vol
2 pwh
2
h
w2
pw
4
w
2
p
p
2
2
h
w2
pw
h
4
208
Si la que gira es una sección triangular se tiene:
h(y)
d
y
P(x) c
El volumen de la capa representativa de este rectángulo es
V = 2 p(y) h(y) y
Si se toman n capas el volumen del sólido de revolución será
aproximadamente:
n
Vol.Sólido
2 p ( y i ) h( y i ) y
i 1
Si n
se tiene
d
n
Vol.Sólido lim
n
2 p ( y i ) h( y i ) y
2
i 1
p( y )h( y )dy
c
Por tanto, cuando se aplica el método de capas con eje de revolución horizontal
se tiene:
d
Vol.Sólido 2
phdy
c
Si el eje de revolución es vertical tendremos:
d
Vol.Sólido 2
ph dx
c
209
Ejemplo 1 Calcular el volumen del sólido engendrado al girar la región
acotada por
y = x ; y = 0 ; x = 4 por revolución en torno de: a) el eje x b) el eje y c) la
recta x = 4 d) la recta x = 6.2
a) Eje x
y
x = y2
dy
y
dx
2
Vol
2
2
2
4
yy dy
3
2
0
y dy
y4
4
2
0
b) Eje y
2
x
2
4
0
24
04
2
(2 4 ) 8
y
y=x1/2
x
4
Vol 2
4
x x dx
0
dx
x 3 / 2 dx
2
0
2
4
2 5/ 2
x
5
x
4
0
4
45 / 2
5
128
5
2 LARSON HOSTETLER, Cálculo y Geometría Analítica Mc Graw Hill, 1986 Pag 287
210
c) x = 4
y
x=4
y=x1/2
dx
4
Vol 2
(4 x) x dx 2
4 3/ 2
4
3
x
4
0
4
4-x
(4 x
1/ 2
x
3/ 2
)dx 2
0
4
5/ 2
5
d) x = 6
32 32
3 5
4
4x3/ 2
3/ 2
x5/ 2
5/ 2
4
0
256
15
y
x=6
y=x1/2
dx
4
Vol
2
(6 x) x dx
2 43 / 2
x
4
2
0
4
6-x
(6 x
1/ 2
x
3/ 2
0
4
5/ 2
5
4 16
32
5
)dx
2
6x3/ 2
3/ 2
x5/ 2
5/ 2
4
0
192
5
8.3 LONGITUD DE ARCO
Sin duda esta constituye otra apasionante aplicación del cálculo integral pues,
nos permite determinar la longitud de una curva sin importar su forma o
ubicación. El procedimiento consiste en dividir la curva en pequeños
211
segmentos de recta del siguiente modo:
y2
y1
y0
a
x1
x2
x3
x4
x5
x6
b
La longitud del segmento comprendido entre los puntos 1 y 2 es:
d
( x2
x1 ) 2
y1 ) 2
( y2
La longitud de todos los segmentos rectilíneos será:
( x1
x0 )2
( y1
( xn
xn 1 )2
......
y0 )2
( yn
x1 )2
( x2
( y2
y1 )2
.........
yn 1 )2
Llamando Δxi , Δyi a cada intervalo la longitud s aproximada de la curva
desde el punto a hasta el punto b es:
n
( xi ) 2
s
( yi ) 2
i 1
En el límite tendremos:
n
s lim
n
n
( xi )
2
lim
yi
xi
1
i 1
b
1
i 1
lim
n
i 1
n
n
( yi )
2
f ' (ci )
2
xi
1
a
2
f ' (ci ) dx
2
xi
212
Por tanto, si y = f(x) tiene derivada continua en [a,b] la longitud de arco entre a
y b viene dada por
b
s
2
1
f ' ( x) dx
a
Si la curva es x = g(y) la longitud de arco entre c y d será:
d
s
2
1
g ' ( y ) dy
c
x4
8
Ejemplo Hallar la longitud de la curva y
1
entre x = 1 ; x = 2
4x 2
La derivada de la función viene dada por:
x3
2
y'
1
2x3
La longitud de la curva
2
s
2
2
1
f '( x) dx
1
1
1
2
1
1
2
1
x4
8
x3
2
x6
4
x3 1
2
2 2 x3
1
2
1
dx
4 x6
1
24
8
1
4 * 22
x6
4
1
4 x2
2
1
32 1 2 4
16
33
16
1
dx
4 x6
2
x3
2
2
1
2 x3
2
1
1
1
2 x3
14
8
dx
2
1
2
2
dx
1
1
4 *12
x6
4
1
dx
4 x6
x3
2
1
dx
2 x3
2
1
16
1
8
1
4
213
8.4 TRABAJO3
8.4.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE
Si un objeto se mueve una distancia D bajo la aplicación de una fuerza
constante F, y en su misma dirección, el trabajo W realizado por esa fuerza se
define como W=FD
8.4.2 TRABAJO REALIZADO POR UNA FUERZA VARIABLE
Supongamos que un objeto se mueve en una línea recta desde x=a hasta x=b
por la acción de una fuerza F(x) que varía de forma continua. Sea ∆ una
partición de [a,b] en n subintervalos determinados por
a = x0 < x1 < x2 < ....... < xn = b
y sea ∆xi = xi – xi-1. Para cada i escogemos ci tal que xi-1 ≤ ci ≤ xi. En ci la fuerza
viene dada por F(ci). Ya que F es continua, y supuestos ∆xi muy pequeños,
concluimos que la fuerza en cada subintervalo es casi constante. Por tanto, el
trabajo realizado al mover el objeto a lo largo del i-ésimo subintervalo, es
aproximadamente
∆Wi = F(ci) ∆xi
Sumando sobre todos los subintervalos, podemos estimar aproximadamente el
trabajo realizado al mover el objeto desde a hasta b por
n
W
Wi
i 1
Más aún, cuanto menor sea ∆xi mejor será la aproximación. Tomando el límite
de esa suma para │∆│→0. ( n→∞ ) tenemos
n
W
lim
n
Wi
i 1
Definimos el trabajo como sigue:
Si un objeto se mueve en línea recta bajo la acción de una fuerza F(x) que varía
de manera continua, y en su misma dirección, el trabajo realizado por esa
fuerza para mover el objeto desde x=a hasta x=b viene dado por:
3 LARSON HOSTETLER, Cálculo y Geometría Analítica Mc Graw Hill, 1986 Pag 299
214
b
n
W
lim
n
Wi
i 1
F ( x )dx
a
Ejemplo 1. Una fuerza de 5 libras comprime un muelle de 15 pulgadas un total
de 4 pulgadas. ¿Qué trabajo hace falta para comprimirlo 7 pulgadas?
La Ley de Hooke dice F(x) = k x, donde F(x) es la fuerza, k una constante que
depende del muelle y x la distancia comprimida.
F(4) = k 4 = 5, de donde,
k = 5/4
F(x) = 5/4 x
7
W
5
x dx
4
0
5 x2
4 2
7
0
5 49
4 2
245
8
30,625 libras pu lg ada
Problema propuesto. Un tanque cilíndrico, de 12 pies de alto y 8 de radio, se
coloca sobre una torre de modo que su fondo este a 20 pies sobre el suelo.
¿Cuánto trabajo es necesario para llenarlo hasta la mitad por un orificio del
fondo, tomando el agua de un manantial en el suelo?
∆y
20 p
215
8.5 PRESIÓN DE UN FLUIDO
La presión ejercida por un líquido sobre un cuerpo sumergido en él viene dada
por
p=ρh
que es independiente de la forma del recipiente, donde; p es la presión del
fluido, ρ la densidad del fluido, h la altura debajo de la superficie o
profundidad. Para una región plana sumergida horizontalmente la fuerza total F
sobre la región plana será:
F=ρhA
Sea una región plana vertical sumergida en un fluido de densidad ρ como se ve
en la figura. Deseamos hallar la fuerza total que actúa sobre esa región, desde
la profundidad h – a hasta h – b.
Consideremos el rectángulo representativo ∆y de longitud Li con yi un punto
del i-ésimo intervalo. La fuerza que actúa sobre ese rectángulo representativo
es
∆Fi = ρ (profundidad)(área) = ρ ( h – yi ) Li ∆y
Superficie del fluido
h-yi
h-yi
b
∆y
yi
h
a
Li
La fuerza que actúa sobre los n rectángulos de este tipo es:
n
n
Fi
i 1
(h yi ) Li y
i 1
Tomando el límite cuando │∆│→0 ( n→∞ ) se tiene la fuerza total sobre la
región
216
n
F
lim
(h yi ) Li y
n
i 1
Por tanto, la fuerza ejercida por un fluido de densidad constante ρ sobre una
región plana, sumergida verticalmente entre y=a e y=b, viene dada por
b
F
(h y ) Ldy
a
donde h denota la profundidad total del fluido y L la longitud horizontal de la
región en y.
Ejemplo. Hallar la fuerza en libras sobre la cara lateral vertical de un depósito
que tiene la forma de un rectángulo y que se encuentra lleno de agua.
3-y
3
∆y
4
3
3
F
profundidad area
0
3
F
4
(3 y )dy
4
3y
0
F
4
(3 y )4dy
0
9
9
2
4(62,4)
9
2
y2
2
3
4
3 3
0
32
2
0
1123,2 libras
8.6 MOMENTOS CENTROS DE MASA Y CENTROIDES 4
El momento que produce una cierta masa respecto al punto P es
4 LARSON HOSTETLER, Cálculo y Geometría Analítica Mc Graw Hill, 1986 Pag 311
217
Momento = (masa) (brazo del momento)
Donde el brazo del momento es la distancia de la masa al punto P.
El momento de un sistema respecto al origen es
n
M0
m1 x1 m2 x2 .........
mn xn
mi xi
i 1
Si el momento es cero el sistema está en equilibrio.
Consideremos un sistema que no esté en equilibrio, y desplacemos el punto de
apoyo a un cierto x = x’ de modo que el sistema quede ya en equilibrio. De
manera que:
n
mi ( xi
x' )
m1 ( x1 x' ) m2 ( x2
x' ) ..... mn ( xn
x' )
0
i 1
o sea
n
n
mi xi
mi x'
i 1
0
i 1
n
mi xi
x'
i 1
n
mi
momento del sistema respecto al origen
masa total del sistema
i 1
Ese punto x’ de balanceo en equilibrio, se llama centro de masas del sistema.
8.6.1 DEFINICIÓN DEL MOMENTO DE UN SISTEMA LINEAL
El momento respecto al origen de un sistema de masas m1, m2, .....,mn,
colocadas en los puntos x1, x2, ... , xn, es:
M0 = m1 x1 +m2 x2 + ... + mn xn
Si la masa total del sistema es m, su centro de masas x’ viene dado por:
x’ = M0/m
8.6.2 DEFINICIÓN DE LOS MOMENTOS DE UN SISTEMA
BIDIMENSIONAL
Para un sistema de masas m1, m2, ....., mn, colocadas en los puntos (x1, y1),
(x2,y2) ... ,( xn, yn) del plano xy, el MOMENTO My RESPECTO AL EJE Y es
218
My = m1 x1 +m2 x2 + ... + mn xn
Y el MOMENTO MX RESPECTO AL EJE X es
Mx = m1 y1 +m2 y2 + ... + mn yn
Si la masa total del sistema es m, el centro de masas (x’, y’) viene dado por:
x’ = My/m
y’ = Mx/m
y
y=f(x)
y=g(x)
y1
(xi, yi)
a
x1
b
x
Sea la lámina de la figura de densidad constante ρ, el rectángulo representativo
se ha obtenido subdividiendo [a,b] en n subintervalos de anchuras ∆x. Si
denotamos por (xi, yi) el centro de masas del i-ésimo rectángulo, la regla del
punto medio lleva a que:
yi
f ( xi ) g ( xi )
2
La masa del i-ésimo rectángulo es:
Masa = (densidad) (área) = ρ [ ∆Ai ] = ρ [f(xi) – g(xi)] (∆x)
Siendo la masa total aproximadamente
219
n
m
[ f ( xi ) g ( xi )]( x)
i 1
tomando el límite para │∆│→0 (n→∞), obtenemos como definición de la
masa
b
m
[ f ( x) g ( x)]dx
A
a
donde A es el área de la lámina.
El momento respecto del eje x del i-ésimo rectángulo es
Momento = (masa)(brazo del momento)=(ρ∆Ai)(yi)=ρ(yi)(∆Ai)
f ( xi ) g ( xi )
[ f ( xi ) g ( xi )] x
2
[ f ( xi ) 2
g ( xi ) 2 ] x
Sumando todos esos momentos y tomando el límite cuando n→∞, obtenemos
el momento respecto al eje x definido como
b
Mx
2
[ f ( x) 2
g ( x) 2 ]dx
x[ f ( x)
g ( x) ]dx
a
para el momento del eje y
b
My
a
8.6.3 MOMENTOS DE UNA LÁMINA PLANA
Sean g ≤ f funciones continua en [a,b]. Para la lámina plana, de densidad
uniforme ρ, acotada por y = g(x), y = f(x), x = a, x = b, los momentos respecto
a los ejes x, y vienen dados por:
b
Mx
2
b
[ f ( x) 2
a
g ( x) 2 ]dx
My
x[ f ( x)
a
g ( x) ]dx
220
la masa m de la lámina viene dada a su vez por
b
m
[ f ( x) g ( x)]dx
A
a
y el centro de masas (x’, y’) por
My
Mx
m
m
Ejemplo. Hallar Mx, My, (x’, y’) para la lámina de densidad uniforme ρ
x , y = 0, x = 4.
acotada por y
x'
y'
b
Mx
Mx
2
4
[ f ( x) 2
g ( x) 2 ]dx
a
x2
2 2
4
0
42
2 2
g ( x) ]dx
a
x dx
0
x( x 0)dx
0
4
x
0
2
4
x[ f ( x)
My
0
4
b
My
2
4
[( x ) 2 0]dx
3/ 2
dx
x5 / 2
5/ 2
4
0
2 5/ 2
4
5
2
32
5
64
5
221
4
m
x dx
0
x'
My
m
64
5
16
3
x3 / 2
3/ 2
12
5
4
0
2 3/ 2
4
3
y'
16
3
Mx
m
4
16
3
3
4
8.7 CENTROIDE DE UNA REGIÓN PLANA
El centro de masas de una lámina uniforme sólo depende de la forma de ésta,
no de densidad, por tanto, podemos generalizar la fórmula del centro de masas
de una lámina para hallar el centro de una región ‘sin masa’ del plano. Cuando
hagamos tal cosa, llamaremos a (x’, y’) el centroide de esa región.
Sean g ≤ f funciones continuas en [a, b]. El centroide (x’, y’) de la región
acotada por y=g(x), y=f(x), x=a, x=b viene dado por
b
b
x[ f ( x)
x'
g ( x) ]dx
a
A
y'
1
[ f ( x) 2
2a
g ( x) 2 ]dx
A
donde A es el área de la región.
Ejemplo. Hallar el centroide de la región acotada por y = x2, y = x
222
1
x2
2
2
A
( x x )dx
0
x3
3
1
1 1
2 3
0
1
6
El centroide estará dado por
b
1
x[ f ( x)
x'
x( x x 2 )dx
g ( x) ]dx
a
A
x' 6
x3
3
x4
4
1/ 6
1
6
0
1
3
1
4
b
y'
2
g ( x) ]dx
A
x5
5
1
12
x 3 )dx
0
1
2
1
1
[ f ( x) 2
2a
x3
y' 3
3
6
1
6 (x2
0
1
3
0
1 1
3 5
1
[ x 2 x 4 ]dx
20
1/ 6
3
2
15
2
5
8.8 SUPERFICIES DE REVOLUCIÓN
Si la gráfica de una función continua se hace girar alrededor de un eje, la
superficie resultante se denomina superficie de revolución.
L
L
R
r
eje de revolución
Cuando el segmento L se hace girar sobre el eje, engendra un tronco de un
cono, cuya área lateral es
223
area lateral
R r
2
2
L
(R r)L
Supongamos que la gráfica de una función f, con derivada continua en [a, b],
gira alrededor del eje x, para engendrar una superficie de revolución, tal como
se ilustra en la siguiente figura. Sea ∆ una partición de [a, b] en subintervalos
de anchuras ∆xi. Entonces el segmento rectilíneo de longitud
Li
xi
2
yi2
y=f(x)
a=x0
xi-1 xi b=xn
∆Li
∆yi
∆xi
genera un cono truncado cuya área lateral, ∆Si viene dada por
Si
Ri
f ( xi 1 )
f ( xi 1 )
ri
Li
f ( xi )
f ( xi ) 1
f ( xi 1 )
xi2
f ( xi ) Li
yi2
xi
yi
2
xi
Por aplicación del teorema del valor medio e del teorema del valor intermedio,
podemos concluir la existencia de un ci y di en (xi-1, xi) tales que
224
f ' (ci )
f ( xi ) f ( xi 1 )
xi xi 1
yi
xi
y
f (d i )
f ( xi 1 ) f ( xi )
2
por tanto
Si
2 f (di ) 1 [ f ' (ci )]2 xi
el área total puede estimarse aproximadamente como
n
S
f (d i ) 1 [ f ' (ci )] 2 xi
2
i 1
tomando el límite cuando │∆│→0 (n→∞) obtenemos
n
S
f (di ) 1 [ f ' (ci )]2 xi
2 lim
n
i 1
b
S
f ( x) 1 [ f ' (ci )]2 dx
2
a
del mismo modo se demuestra que, si la gráfica de f gira alrededor del eje y, el
área S viene dada por
b
S
x 1 [ f ' (ci )]2 dx
2
a
En ambas fórmulas para S, podemos mirar los productos 2 π f(x) y 2 π x
como asociados a las circunferencias descritas por un punto (x, y) de loa
gráfica de f en su rotación en torno a los respectivos ejes x e y.
8.8.1 ÁREA DE UNA SUPERFICIE DE REVOLUCIÓN
Si y = f(x) tiene derivada continua en el intervalo [a, b], entonces el área S de la
superficie de revolución que engendra esa gráfica en {a, b} es:
1.- Si gira en torno al eje x
b
S
f ( x) 1 [ f ' (ci )]2 dx
2
a
225
2.- Si gira en torno al eje y
b
S
x 1 [ f ' (ci )]2 dx
2
a
Ejemplo. Hallar el área de la superficie engendrada por rotación de la gráfica
de f(x)=x3, en su intervalo [0,2], alrededor del eje x
f ’(x) = 3 x2
El área será
2
S
2
2
2
f ( x) 1 [ f ' ( x)] dx
0
0
2
S
2
x 3 1 [9 x 4 ]dx
2
0
S
x 3 1 [3x 2 ]2 dx
2
(1 9 x 4 )3 / 2
18
3/ 2
2
36 x 3 1 [9 x 4 ]dx
36 0
2
203,043
0
226
FÓRMULAS BÁSICAS DE INTEGRACIÓN
un 1
C; n
n 1
1) u nu ' dx
2) euu' dx eu C
1
u'
dx ln u C
u
5) (cosu)u' dx sin u C
4) (sin u)u' dx
3)
7) (csc2 u)u' dx
(sec2 u)u' dx tan u C
6)
cot u C
cosu C
8) (secu. tan u)u' dx secu C
9) (cscu. cotu)u' dx
cscu C 10) (tan u)u' dx
11) (cotu)u' ln sin u
C
12) (secu)u' dx
ln secu tan u
C
13) (cscu)u' dx
ln cscu cotu
C
u'
14 )
a
16 )
2
u
2
u'
2
2
dx
arcsin
dx
ln u
u a
u'
17 ) 2
dx
u a2
18)
19 )
u' dx
u u 2 a2
u ' dx
u a2 u2
u
C
a
u2
15)
a2
u'
a
C
1 u a
ln
C
2a u a
u
1
arc sec
C
a
a
u
a
ln
a
u2
u
a2
C
2
u
2
dx
ln cosu
C
1
u
arctan
C
a
a