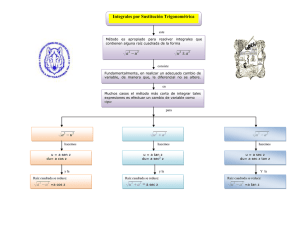
Reglas para Derivar (con expresiones trigonométricas)

REGLAS PARA DERIVAR
(con expresiones trigonométricas)
FUNCIÓN : f(x)
DERIVADA : f ’(x)
C = cualquier número Real
0
x
x
1
cx
c
n
(n es cualquier número Real)
n  x n1
c  xn
c  n  x n1
c  u (x)
c  u , ( x)
REGLA DE LA SUMA Y LA RESTA
a( x)  b( x)
a, ( x)  b, ( x)
Elaboró: Ing. Julio Alberto Ríos Gallego www.julioprofe.net www.youtube.com/user/julioprofe
REGLAS PARA DERIVAR
(con expresiones trigonométricas)
Continuación
FUNCIÓN : f(x)
DERIVADA : f ’(x)
REGLA DEL PRODUCTO
a( x)  b( x)
a, ( x)  b( x)  a( x)  b, ( x)
REGLA DEL COCIENTE
a( x)
b( x )
a, ( x)  b( x)  a( x)  b, ( x)
b( x) 2
REGLA DE LA CADENA
H u(x)
H , u ( x)  u , ( x)
REGLA DE LA CADENA PARA POTENCIAS
u( x)n
n  u( x) n 1 u, ( x)
Elaboró: Ing. Julio Alberto Ríos Gallego www.julioprofe.net www.youtube.com/user/julioprofe
REGLAS PARA DERIVAR
(con expresiones trigonométricas)
Continuación
FUNCIÓN : f(x)
DERIVADA : f ’(x)
FUNCIONES TRIGONOMÉTRICAS
sen x
sen u(x)
cos x
cos u(x)
cos x
cos u(x)  u ,(x)
 sen x
 sen u(x)  u ,(x)
sec 2 x
tan x
tan u(x)
sec 2u(x)  u ,(x)
cot x
 csc 2 x
cot u(x)
 csc 2u(x)  u ,(x)
sec x
sec u(x)
csc x
csc u(x)
sec x  tan x
sec u(x)  tan u(x)  u ,(x)
 csc x  cot x
 csc u(x)  cot u(x)  u ,(x)
Elaboró: Ing. Julio Alberto Ríos Gallego www.julioprofe.net www.youtube.com/user/julioprofe
REGLAS PARA DERIVAR
(con expresiones trigonométricas)
Continuación
FUNCIÓN : f(x)
DERIVADA : f ’(x)
FUNCIÓN EXPONENCIAL
a
a
a
x
u( x)
a
u(x)
 ln a  u ,(x)
x
e
u ( x)
e
 ln a
x
e
e
u ( x)
x
 u , ( x)
FUNCIÓN LOGARÍTMICA
log a x
log a u(x)
ln x
ln u(x)
1
x  ln a
u ,(x)
u(x)  ln a
1
x
u , ( x)
u ( x)
Elaboró: Ing. Julio Alberto Ríos Gallego www.julioprofe.net www.youtube.com/user/julioprofe
REGLAS PARA DERIVAR
(con expresiones trigonométricas)
Continuación
FUNCIÓN : f(x)
DERIVADA : f ’(x)
FUNCIONES TRIGONOMÉTRICAS INVERSAS
1
sen x  arcsen x
sen1u(x)  arcsen u(x)
1
cos x  arccos x
cos 1u(x)  arccos u(x)
1
tan x  arctan x
tan 1u(x)  arctan u(x)
1
1  x2
u ,(x)
1  u(x) 2
1
1  x2
 u ,(x)
1  u(x) 2
1
1  x2
u ,(x)
1  u(x) 2
Elaboró: Ing. Julio Alberto Ríos Gallego www.julioprofe.net www.youtube.com/user/julioprofe
FUNCIÓN : f(x)
DERIVADA : f ’(x)
FUNCIONES TRIGONOMÉTRICAS INVERSAS (continuación)
1
1  x2
 u ,(x)
1
cot x  arccot x
cot 1u(x)  arccot u(x)
1  u(x) 2
1
1
sec x  arcsec x
sec1u(x)  arcsec u(x)
x  x2  1
u ,(x)
u(x) 
1
1
csc x  arccsc x
csc1u(x)  arccsc u(x)
u(x) 2  1
x  x2  1
 u ,(x)
u(x) 
u(x) 2  1
Elaboró: Ing. Julio Alberto Ríos Gallego www.julioprofe.net www.youtube.com/user/julioprofe