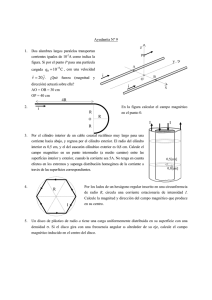
Libro de Apuntes del Curso

Universidad de Santiago de Chile.
Facultad De Ciencia.
Departamento de Física.
Dr. Juan Escrig Murúa.
Dr. Carlos López Cabrera.
Introducción al
ELECTROMAGNETISMO
Proyecto de innovación docente de la Vicerrectoría Académica.
Ingeniería Física
Santiago - Chile
♠
libro para el curso de Electromagnetismo I
Universidad de Santiago de Chile.
Autor
Dr. Juan Escrig Murua
Dr. Carlos López Cabrera
Diseño y Diagramación
Pascal Toro
Edición Preliminar
Agosto de 2012
Santiago, Chile.
Las ediciones de este documento se mantendrán actualizadas en la web http:\\uvirtual.usach.cl
Estimado lector: Si tiene algún aporte o crítica sobre el contenido de este apunte, le
agradecemos comunicarlo a los correos,
Dr. Juan Escrig Murúa
[email protected]
Dr. Carlos López Cabrera
[email protected]
Pascal Toro Lagos
[email protected]
Índice general
Índice de figuras
xi
Índice de cuadros
xxiii
Capítulo 1. Electrostática
1.1
1.2
1.3
1
Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1.1
La interacción electromagnética . . . . . . . . . . . . . . . . . . . . . .
1
1.1.2
Historia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
Propiedades de la carga eléctrica . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.2.1
Dualidad de la carga . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.2.2
Conservación de la carga . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.2.3
Cuantización de la carga . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
1.2.4
Carga por inducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
Ley de Coulomb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
1.3.1
Comparación entre la fuerza de gravitación y la fuerza eléctrica . .
10
1.3.1.1
11
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
i
Índice general
ii
1.3.2
Principio de superposición . . . . . . . . . . . . . . . . . . . . . . . . . .
11
1.3.2.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.3.2.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
Energía de un sistema de cargas . . . . . . . . . . . . . . . . . . . . .
13
1.3.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
Campo eléctrico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.3.3
1.4
1.4.0.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.4.0.3
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
1.4.1
Líneas de campo eléctrico . . . . . . . . . . . . . . . . . . . . . . . . . .
20
1.4.2
Movimiento de cargas puntuales en campos eléctricos . . . . . . . .
21
1.4.2.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
Distribuciones continuas de cargas . . . . . . . . . . . . . . . . . . . .
23
1.4.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
1.4.3.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
1.4.3.3
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
Ley de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
1.5.1
Flujo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
1.5.1.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
1.5.2
Ley de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
1.5.3
Principio de superposición . . . . . . . . . . . . . . . . . . . . . . . . . .
34
1.5.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
Campo eléctrico debido a una carga puntual . . . . . . . . . . . . . .
36
1.5.4.1
36
1.4.3
1.5
1.5.4
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Índice general
1.5.4.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
1.5.4.3
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
1.5.4.4
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
1.5.5
Divergencia de una función vectorial . . . . . . . . . . . . . . . . . . .
40
1.5.6
Cálculo de la divergencia en coordenadas cartesianas . . . . . . . .
42
1.5.6.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
1.5.6.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
1.5.6.3
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
El Teorema de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
Potencial Eléctrico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
1.6.1
Integral curvilínea del campo eléctrico . . . . . . . . . . . . . . . . . .
47
1.6.1.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
1.6.2
Diferencia de potencial . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
1.6.3
Diferencia de potencial en un campo eléctrico uniforme . . . . . . .
50
1.6.4
Superficies equipotenciales . . . . . . . . . . . . . . . . . . . . . . . . .
51
1.6.4.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
1.6.4.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
1.6.5
Gradiente de una función escalar . . . . . . . . . . . . . . . . . . . . .
53
1.6.6
Deducción del campo eléctrico a partir del potencial . . . . . . . . .
53
1.6.6.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
54
Potencial eléctrico de cargas puntuales . . . . . . . . . . . . . . . . .
54
1.6.7.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
55
1.6.7.2
Ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
1.5.7
1.6
iii
1.6.7
Índice general
iv
1.6.7.3
Ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
Potencial eléctrico para distribuciones continuas de carga . . . . . .
57
1.6.8.1
Ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
1.6.8.2
Ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
1.6.8.3
ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
1.6.8.4
ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
Laplaciana . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
1.6.10 Ecuación de Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
1.6.11 Rotacional de una función vectorial . . . . . . . . . . . . . . . . . . . .
60
1.6.12 Teorema de Stokes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
1.6.13 El rotacional en coordenadas cartesianas . . . . . . . . . . . . . . . .
63
1.6.14 Significado físico del rotacional . . . . . . . . . . . . . . . . . . . . . .
64
Campo eléctrico en conductores . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
1.7.1
Clasificación de los materiales . . . . . . . . . . . . . . . . . . . . . . .
65
1.7.2
Conductores en equilibrio electrostático . . . . . . . . . . . . . . . . .
66
1.7.3
Potencial eléctrico debido a un conductor cargado . . . . . . . . . . .
68
1.7.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
69
1.7.4
Método de las imágenes . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
1.7.5
Elementos en circuitos eléctricos . . . . . . . . . . . . . . . . . . . . . .
72
1.7.6
Definición de la capacitancia . . . . . . . . . . . . . . . . . . . . . . . .
73
1.7.6.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
1.7.6.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
Circuito eléctricos básicos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
1.6.8
1.6.9
1.7
1.8
Índice general
v
1.8.1
Capacitores en paralelo . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
1.8.2
Capacitores en serie . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
1.8.2.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
1.8.2.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
Energía almacenada en un capacitor cargado . . . . . . . . . . . . . .
80
1.8.3
Capítulo 2. Transporte eléctrico
2.1
2.2
105
Corriente eléctrica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
2.1.1
Transporte de carga y densidad de corriente . . . . . . . . . . . . . . 105
2.1.2
Corrientes estacionarias . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
2.1.2.1
Ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
2.1.2.2
Ejercicio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
Ley de Ohm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
2.2.1
Conductividad eléctrica y Ley de Ohm . . . . . . . . . . . . . . . . . . 110
2.2.1.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
2.2.1.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
2.2.1.3
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
2.2.2
Modelo de conducción eléctrica . . . . . . . . . . . . . . . . . . . . . . 115
2.2.3
Resistencia y temperatura . . . . . . . . . . . . . . . . . . . . . . . . . . 117
2.2.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
2.2.4
Superconductores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
2.2.5
Potencia eléctrica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
2.2.5.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
2.2.5.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
Índice general
vi
2.3
Circuitos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
2.3.1
Fuerza electromotriz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
2.3.1.1
2.3.2
2.3.3
2.3.4
Resistores en serie y en paralelo . . . . . . . . . . . . . . . . . . . . . 125
2.3.2.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
2.3.2.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
Leyes de Kirchhoff . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
2.3.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
2.3.3.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
Carga de un condensador . . . . . . . . . . . . . . . . . . . . . . . . . . 132
2.3.4.1
2.3.5
2.3.6
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
Descarga de un capacitor . . . . . . . . . . . . . . . . . . . . . . . . . . 135
2.3.5.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
2.3.5.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
Medidores eléctricos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
Capítulo 3. Magnetismo
3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125
149
Campo de inducción magnético . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
3.1.1
Historia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
3.1.2
Campos y fuerzas magnéticas . . . . . . . . . . . . . . . . . . . . . . . . 151
3.1.3
Diferencias entre fuerza eléctrica y magnética . . . . . . . . . . . . . 152
3.1.3.1
3.1.4
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
Movimiento de una partícula cargada en un campo magnético
uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
Índice general
3.1.5
vii
3.1.4.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
3.1.4.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
Fuerza magnética que actúa sobre un conductor que transporta
corriente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
3.1.5.1
3.1.6
3.1.7
3.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160
Ley de Biot-Savart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
3.1.6.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
3.1.6.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
Fuerza magnética entre dos conductores paralelos . . . . . . . . . . 165
Ley de Ampere . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
3.2.0.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
3.2.0.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
3.2.1
Campo magnético debido a un solenoide . . . . . . . . . . . . . . . . . 172
3.2.2
Potencial vector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
Capítulo 4. Inducción Electromagnética
4.1
183
Ley de inducción de Faraday . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
4.1.1
¿Cómo Faraday dedujo la Ley de Inducción? . . . . . . . . . . . . . . . 185
4.1.2
Ley de Gauss en Magnetismo . . . . . . . . . . . . . . . . . . . . . . . . 186
4.1.3
Ley de Inducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 187
4.1.3.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 188
4.1.4
Aplicación de la Ley de Faraday . . . . . . . . . . . . . . . . . . . . . . 189
4.1.5
Circuito moviéndose en un campo magnético fijo . . . . . . . . . . . . 190
4.1.5.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
Índice general
viii
4.1.6
Circuito fijo y un campo magnético variable . . . . . . . . . . . . . . . 192
4.1.7
Ley de Lenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193
4.1.8
Fem en movimiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195
4.1.8.1
4.1.9
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197
Generadores y motores . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
4.1.10 Generación de corriente alterna . . . . . . . . . . . . . . . . . . . . . . 200
4.1.11 Corrientes de Foucault . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201
4.1.12 Inductancia Mutua y Autoinductancia . . . . . . . . . . . . . . . . . . . 203
4.1.12.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206
4.1.12.2
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 208
4.1.13 Energía magnética . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209
4.1.14 Densidad de energía magnética . . . . . . . . . . . . . . . . . . . . . . 210
4.1.14.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
4.1.15 Circuitos RL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211
4.1.16 Oscilaciones libres en un circuito LC . . . . . . . . . . . . . . . . . . . 213
4.1.16.1
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215
4.1.17 Oscilaciones amortiguadas: Circuito RLC . . . . . . . . . . . . . . . . . 217
4.2
Corriente Alterna (AC) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219
4.2.1
Reactancias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 220
4.2.2
Impedancia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224
4.2.3
Valor eficaz y potencia media . . . . . . . . . . . . . . . . . . . . . . . . 225
4.2.4
Resonancia: Circuito RLC . . . . . . . . . . . . . . . . . . . . . . . . . . 228
4.2.5
Transformadores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
Índice general
ix
4.2.5.1
4.2.6
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232
Filtros . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232
Capítulo 5. Campos en la Materia
5.1
Campo eléctrico en la materia . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249
5.1.1
Dipolo eléctrico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249
5.1.2
Ejemplos de dipolos en la escala microscópica . . . . . . . . . . . . . 251
5.1.3
Dipolo en un campo uniforme . . . . . . . . . . . . . . . . . . . . . . . . 252
5.1.4
Energía potencial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253
5.1.5
Dieléctricos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253
5.1.6
Polarización homogénea . . . . . . . . . . . . . . . . . . . . . . . . . . . 256
5.1.7
Polarización inhomogénea . . . . . . . . . . . . . . . . . . . . . . . . . . 258
5.1.7.1
5.1.8
5.2
249
Ejemplo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 259
Energía . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 260
Magnetismo en la Materia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 260
5.2.1
Corrientes de magnetización . . . . . . . . . . . . . . . . . . . . . . . . 260
5.2.2
~ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262
El campo B
5.2.3
Ecuación constitutiva . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262
5.2.4
La razón giromagnética . . . . . . . . . . . . . . . . . . . . . . . . . . . 263
5.2.5
Diamagnetismo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265
5.2.6
Paramagnetismo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
5.2.7
Ferromagnetismo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
5.2.8
Los dominios de Weiss . . . . . . . . . . . . . . . . . . . . . . . . . . . . 273
5.2.9
Circuitos magnéticos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274
Índice general
x
Capítulo 6. Ecuaciones de Maxwell
6.1
6.2
283
Ecuaciones de Maxwell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 283
6.1.1
Revisión de las leyes generales . . . . . . . . . . . . . . . . . . . . . . 283
6.1.2
Corriente de desplazamiento . . . . . . . . . . . . . . . . . . . . . . . . 285
Ondas electromagnéticas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
6.2.1
La ecuación de ondas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
6.2.2
Ondas electromagnéticas planas . . . . . . . . . . . . . . . . . . . . . . 289
6.2.3
Ondas planas monocromáticas . . . . . . . . . . . . . . . . . . . . . . . 291
6.2.4
Energía y vector de Poynting . . . . . . . . . . . . . . . . . . . . . . . . 292
Anexos
297
Capítulo A. Prefijos y letras griegas
299
Capítulo B. Derivadas vectoriales
301
Capítulo C. Constantes Físicas
303
Capítulo D. Premios Nobel de Física
305
Bibliografía
311
Índice de figuras
1.1
Mapa de Grecia que muestra la ubicación de Magnesia.[1] . . . . . . . . . .
3
1.2
Experimento entre una barra de caucho y una de vidrio, que demuestra
que existe una fuerza de atracción y/o de repulsión entre sistemas cargados.
4
1.3
Fuerza de interacción entre dos cargas eléctricas. . . . . . . . . . . . . . . . .
6
1.4
Experimento que explica el Principio de Conservación de la Carga. . . . . .
7
1.5
Inducción de carga sobre una esfera conductora. . . . . . . . . . . . . . . . .
8
1.6
Balanza de torsión de Coulomb. . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.7
Principio de superposición de la fuerza de Coulomb. . . . . . . . . . . . . . .
12
1.8
ejercicio para tres cargá puntuales en dos dimensiones. . . . . . . . . . . . .
13
1.9
Sistema de dos cargas que se acercan desde el infinito. . . . . . . . . . . . .
14
1.10 Sistema de tres cargas que se acercan desde el infinito. . . . . . . . . . . . .
15
1.11 Ejercicio para un cubo hecho de cargas. . . . . . . . . . . . . . . . . . . . . . .
16
1.12 Líneas de Campo de temperatura. . . . . . . . . . . . . . . . . . . . . . . . . . .
17
1.13 Campo de velocidades. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
1.14 Representación del campo gravitacional generado por la Tierra. . . . . . . .
18
1.15 ejemplo-campo-eléctrico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.16 Líneas de Campo Eléctrico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
xi
xii
Índice de figuras
1.17 Carga eléctrica en movimiento en presencia de un campo eléctrico uniforme. 22
1.18 Distribución continua de la carga. . . . . . . . . . . . . . . . . . . . . . . . . . .
23
1.19 Línea de carga continua. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
1.20 Anillo uniformemente cargado de radio a, el campo en P sobre el eje x es
debido aun elemento de carga ∆q. . . . . . . . . . . . . . . . . . . . . . . . . .
26
1.21 Disco uniformemente cargado de radio R. . . . . . . . . . . . . . . . . . . . . .
27
~ La superficie se
1.22 Superficie arbitraria inmersa en un campo eléctrico E.
divide en pequeños segmentos de superficie de área ∆Ai . . . . . . . . . . . .
29
1.23 Líneas de fuerzas correspondientes a un campo eléctrico uniforme
perpendicular al área A, pero que forma un ángulo θ con el vector de
unidad n̂ normal al área A0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
1.24 Superficie en forma de cubo en un campo eléctrico uniforme paralelo al
eje x. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
1.25 Campo eléctrico generado por una carga puntual q, localizada en una
esfera de radio r. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
1.26 Superficies cerradas de varias formas, circundando una carga q. . . . . . .
33
1.27 Carga puntual localizada afuera de una superficie cerrada, donde las líneas
que entran es igual al número que salen de ella. . . . . . . . . . . . . . . . .
34
1.28 Distintas superficies cerrando cargas q1 , q2 y q3 . . . . . . . . . . . . . . . . .
35
1.29 La carga q está en el centro de una superficie esférica Gaussiana, donde
~ es paralelo a dA en cualquier punto sobre la superficie. . . . . . . . . . .
E
36
1.30 Esfera aislante uniformemente cargada de radio a y carga total Q. . . . . .
37
1.31 Cascarón esférico uniformemente cargado. . . . . . . . . . . . . . . . . . . . .
38
1.32 Línea infinita de carga positiva rodeada por una superficie gaussiana
cilíndrica concéntrica con la línea de carga. . . . . . . . . . . . . . . . . . . .
39
1.33 Superficie gaussiana cilíndrica para el cálculo del campo eléctrico, que
penetra un plano infinito de carga positiva. . . . . . . . . . . . . . . . . . . . .
40
Índice de figuras
xiii
1.34 Trabajo de campo eléctrico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
1.35 Diferencia de potencial entre dos puntos A y B en un campo eléctrico
uniforme. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
1.36 Campo uniformemente dirigido, donde B está a un potencial más bajo que
el punto A. Los puntos B y C están al mismo potencial. . . . . . . . . . . . .
51
1.37 Diferencia de potencial entre los puntos A y B debido a la carga puntual q. 54
1.38 Dipolo eléctrico, separado por una distancia 2a . . . . . . . . . . . . . . . . .
57
1.39 Barilla de carga uniforme Q colocada a los largo del eje x. . . . . . . . . . .
58
1.40 integral de línea de un cierto campo vectorial F~ sobre un camino cerrado
C el cual es el contorno de una superficie S. . . . . . . . . . . . . . . . . . . .
61
1.41 División del el camino cerrado C en dos. . . . . . . . . . . . . . . . . . . . . .
61
1.42 Asociamos a cada superficie ai su vector normal n̂i mediante la regla de
la mano derecha para su sentido. . . . . . . . . . . . . . . . . . . . . . . . . . .
62
1.43 Bucle en el plano xy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
1.44 Lámina conductora en un campo eléctrico externo Eext . . . . . . . . . . . . .
66
1.45 Superficie gaussiana en el interior de un conductor de forma arbitraria. . .
67
1.46 Flujo a través de una superficie gaussiana en forma cilíndrica, para un
conductor cargado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
1.47 Conductor de forma arbitraria con un exceso de cargas positivas. . . . . . .
69
1.48 Sistema equidistantes para una carga y su carga imagen. . . . . . . . . . . .
71
1.49 Sistema de dos placas planas conductoras cargadas separadas por una
distancia d . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
1.50 Conductor cilíndrico de radio a, rodeado por un cascarón cilíndrico coaxial
de radio b. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
1.51 Símbolos en circuitos para condensadores, baterías, conductores e
interruptores. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
xiv
Índice de figuras
1.52 Conexión en paralelo de dos condensadores, donde la diferencia de
potencial aplicada a ambos es la misma. . . . . . . . . . . . . . . . . . . . . .
77
1.53 Conexión en serie de dos condensadores, donde la diferencia de potencial
es la suma de las diferencias aplicada a los condensadores individuales. .
78
1.54 Red de condensadores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
1.55 Trabajo necesario para cargar un condensador . . . . . . . . . . . . . . . . . .
81
1.56 (Problema 4). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
84
1.57 (Problema 5). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
84
1.58 (Problema 6). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
1.59 (Problema 7 y 9). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
1.60 (Problema 13). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
1.61 (Problema 14). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
1.62 (Problema 19). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
1.63 (Problema 20). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
1.64 (Problema 21). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
89
1.65 (Problema 22). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
90
1.66 (Problema 24). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
1.67 (Problema 25). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
1.68 (Problema 26). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
92
1.69 (Problema 28). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
92
1.70 (Problema 33). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
93
1.71 (Problema 38 y 56). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
1.72 (Problema 40). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
1.73 (Problema 49). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
97
Índice de figuras
xv
1.74 (Problema 51). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
98
1.75 (Problema 54 y 55). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99
1.76 (Problema 60). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
1.77 (Problema 62). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
1.78 (Problema 63). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
1.79 (Problema 66). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
2.1
Cargas en movimiento a través de un rectángulo de área a. . . . . . . . . . . 106
2.2
Cargas en movimiento que atraviesan un prisma en un intervalo ∆t. . . . . 107
2.3
Sección de un alambre portador de corriente. . . . . . . . . . . . . . . . . . . 111
2.4
Gráficos de corriente I en función del voltaje V, para materiales óhmicos y
no óhmicos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
2.5
Cono circular truncado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
2.6
Movimiento aleatorio de un portador de carga en un conductor en ausencia
de campo eléctrico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
2.7
Movimiento aleatorio de un portador de carga en un conductor, en
presencia de campo eléctrico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
2.8
Instante entre colisiones. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
2.9
Gráfico de resistividad ρ en función de la temperatura T . . . . . . . . . . . . 119
2.10 Gráfico de la resistencia del mercurio en función de la temperartura. . . . . 120
2.11 Circuito eléctrico simple, formado por una batería (∆V ), una resistencia
(R) y cables de conexión. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
2.12 Circuito de una fuente de fem ε de resistencia interna r conectada a una
resistencia externa R. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
2.13 variación del potencial en el circuito en serie de a hasta d. . . . . . . . . . 125
2.14 conexión de dos resistencias en serie. . . . . . . . . . . . . . . . . . . . . . . . 126
Índice de figuras
xvi
2.15 conexión de dos resistencias en paralelo. . . . . . . . . . . . . . . . . . . . . . 127
2.16 Circuito formado por resistencias de diferentes valores. . . . . . . . . . . . . 128
2.17
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
2.18 Regla del nodo (unión) de Kirchhoff. . . . . . . . . . . . . . . . . . . . . . . . . 129
2.19 Reglas para determinar los cambios de potencial a través de una
resistencia y una batería. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
2.20 Circuito en serie, donde las polaridades de las baterías están opuestas
una de la otra. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
2.21
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
2.22 Circuito para la carga de un condensador, antes y después de cerrar un
interrupor. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
2.23 Gráficas de carga y corriente para un circuito RC. . . . . . . . . . . . . . . . 134
2.24 Circuito para la descarga de un condensador. . . . . . . . . . . . . . . . . . . 135
2.25
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
2.26 Amperímetro conectado en serie que permite medir la corriente. . . . . . . . 138
2.27 Voltímetro conectado en paralelo que permite medir la diferencia de
potencial. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
2.28 (Problema 4). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
2.29 (Problema 8). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143
2.30 (Problema 17). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
2.31 (Problema 18). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
2.32 (Problema 19). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
2.33 (Problema 20). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
2.34 (Problema 21). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
2.35 (Problema 22). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
Índice de figuras
xvii
2.36 (Problema 23). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
2.37 (Problema 24). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
3.1
Líneas de campo magnético, dentro y fuera de una barra magnética. . . . . 151
3.2
Dirección y sentido de la fuerza magnética sobre una partícula cargada. . 152
3.3
Partícula cargada que se mueve perpendicular a un campo magnético
uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
3.4
Partícula cargada, que posee una componente de velocidad paralelo a un
campo magnético y otro perpendicular al mismo. . . . . . . . . . . . . . . . . 155
3.5
Alambre vertical flexible sobre un campo. Cuando no existe corriente en
el alambre éste permanece vertical, pero cuando circula corriente este de
desvía hacia la izquierda o derecha según el sentido de la corriente. . . . . 157
3.6
Alambre que lleva una corriente I en un campo magnético externo B. . . . 158
3.7
Conductor curvo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
3.8
Espira de corriente. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160
3.9
Alambre suspendido dentro de un campo magnético. . . . . . . . . . . . . . . 161
~ producido por un conductor rectilíneo indefinido por
3.10 campo magnético B
el que circula una corriente de intensidad I. . . . . . . . . . . . . . . . . . . . 162
3.11 Segmento de alambre recto que lleva una corriente I. . . . . . . . . . . . . . 163
3.12 Espira de corriente.[4] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
3.13 Dos alambres paralelos por los cuales circula una corriente que ejercen
fuerza uno sobre otro. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
3.14 Experimento realizado por Oersted que demuestra que un conductor que
lleva corriente produce un campo magnético.[4] . . . . . . . . . . . . . . . . . . 167
~ a lo largo de un camino cerrado ABCD. . . . . . . . 168
3.15 integral curvilínea de B
3.16 Camino circular que rodea un conductor . . . . . . . . . . . . . . . . . . . . . . 169
Índice de figuras
xviii
3.17 Camino irregular C que rodea un conductor. . . . . . . . . . . . . . . . . . . . 169
3.18 Camino irregular C 0 que rodea un conductor. . . . . . . . . . . . . . . . . . . . 170
3.19 Bobina toroidal.[4] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
3.20 Líneas de campo magnético para un solenoide de vueltas estrechas con
longitud finita y corriente constante.[4] . . . . . . . . . . . . . . . . . . . . . . . 172
3.21 (Problema 05). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
3.22 (Problema 06). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
3.23 (Problema 08). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
3.24 (Problema 11). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
3.25 (Problema 12). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180
4.1
Inducción de una fem utilizando un campo magnético variable. . . . . . . . . 184
4.2
Experimento de Faraday. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185
4.3
Líneas de campo eléctrico de un dipolo eléctrico se inician en la carga
positiva y terminan en la carga negativa. . . . . . . . . . . . . . . . . . . . . . 186
4.4
Líneas de campo magnético de un imán de barra formando lazos cerrados. 187
4.5
Espira inmersa en un campo magnético. . . . . . . . . . . . . . . . . . . . . . . 188
4.6
Una cuerda de guitarra eléctrica, que vibra, induce una fem en una bobina
de la recolectora. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
4.7
Dos posiciones sucesivas de C para relacionar la variación del flujo
magnético con la fuerza electromotriz. . . . . . . . . . . . . . . . . . . . . . . . 190
4.8
Imán que se mueve hacia una espira conductora, donde se induce una
corriente. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193
4.9
La corriente inducida produce su propio flujo hacia la izquierda, para
contrarrestar el incremento del flujo externo hacia la derecha. . . . . . . . . 194
Índice de figuras
xix
4.10 Barra conductora moviéndose con una velocidad ν~ a través de un campo
~ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195
magnético B.
4.11 Barra conductora deslizándose a lo largo de dos rieles conductores. La
fuerza magnética F~m se opone al movimiento y un corriente se induce en
la espira en la dirección contraria a las manecillas del reloj. . . . . . . . . . 196
4.12 Motor de inducción.[4] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199
4.13 Diagrama de un generador de corriente AC.[4] . . . . . . . . . . . . . . . . . . 200
4.14 Gráfico de fem alterna en función del tiempo. . . . . . . . . . . . . . . . . . . . 201
4.15 Placa conductora que entra al campo en la posición 1, la corriente de
Foucault es contraria a las manecillas del reloj. . . . . . . . . . . . . . . . . . 202
4.16 Placa del péndulo con ranuras que reducen las corrientes de Foucault. . . 202
4.17 Corte seccional de un cable coaxial largo. . . . . . . . . . . . . . . . . . . . . . 207
4.18 Circuito RL en serie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211
4.19 Circuito RL con dos interruptores. Cuando S1 esta cerrad y S2 esta abierto,
la batería forma parte del circuito. . . . . . . . . . . . . . . . . . . . . . . . . . 212
4.20 Circuito LC en serie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213
4.21 Gráficas de carga y corriente en función del tiempo. . . . . . . . . . . . . . . 215
4.22
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216
4.23 Circuito RLC en serie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217
4.24 Carga en función del tiempo para un circuito RLC amortiguado. . . . . . . . 218
4.25 Bobina de inductances L conectado a un generador de corriente alterna. . 221
4.26 Diagrama de fase para un circuito inductivo . . . . . . . . . . . . . . . . . . . 222
4.27 Condensador de capacidad C conectado a un generador de corriente alterna.223
4.28 Diagrama de fase para un circuito capacitivo . . . . . . . . . . . . . . . . . . . 223
4.29 Gráfico de la corriente al cuadrado en una resistencia en función del tiempo.226
Índice de figuras
xx
4.30 Circuito en serie que consiste en un resistor, un inductor y un condensador
conectado a un generador de corriente alterna. . . . . . . . . . . . . . . . . . 228
4.31 Potencia media en función con la frecuencia de un circuito en serie RLC. . 230
4.32 Transformador ideal compuesto de dos bobinas enrolladas en el mismo
núcleo de hierro. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
4.33 (Problema 10). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 236
4.34 (Problema 11). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 237
4.35 (Problema 16). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 238
4.36 (Problema 30). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240
4.37 (Problema 31). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 241
4.38 (Problema 33). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242
4.39 (Problema 55). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246
4.40 (Problema 56). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246
4.41 (Problema 57). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247
4.42 (Problema 58). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247
5.1
Dipolo eléctrico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250
5.2
Molécula de agua h2 o que tiene una polarización permanente como
resultado de su geometría. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 252
5.3
Dipolo eléctrico en un campo eléctrico uniforme. . . . . . . . . . . . . . . . . . 252
5.4
Carga inducida sobre un dieléctrico colocado entre las placas de un
condensador cargado. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
5.5
Dieléctrico polarizado, en donde los momentos dipolares de las moléculas
se alinean con el campo eléctrico externo y producen una superficie con
carga negativa inducida y otra con carga positiva inducida. . . . . . . . . . . 256
5.6
Aparición de cargas de polarización. . . . . . . . . . . . . . . . . . . . . . . . . 257
Índice de figuras
xxi
5.7
Variación de la polarización de un punto a otro dentro del dieléctrico. . . . 258
5.8
Electron moviéndose en una orbita circular de radio r, momento angular
L y momento magnético µ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
5.9
~ . . . 266
Movimiento de un electron cuando es sometido a un campo externo B
~ . . . . . . . . . . . . . . . . . . 269
~ 0 en un campo externo B.
5.10 dipolo magnético m
5.11 Curvas de histéresis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
5.12 Curva de histéresis para un material ferromagnético. . . . . . . . . . . . . . . 271
5.13 Magnetización en función de la temperatura absoluta para una sustancia
ferromagnética. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272
5.14 Momentos magnéticos polares orientados a al azar en una sustancia no
magnetizada y alineados con el campo magnetizando la muestra. . . . . . . 273
5.15 bobina toroidal utilizada para medir las propiedades magnéticas de un
material. El núcleo se hace del material en estudio. . . . . . . . . . . . . . . 274
5.16 (Problema 02). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
5.17 (Problema 04). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
5.18 (Problema 06). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 279
5.19 (Problema 12). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280
6.1
6.2
la corriente de conducción pasa a través de S1 , pero no a través de S2 .
Sólo el desplazamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286
Onda electromagnética linealmente polarizada en el plano en la dirección
x positiva con una velocidad c. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
xxii
Índice de figuras
Índice de cuadros
1.1
Valores de carga y masa para los componentes del átomo. . . . . . . . . . .
7
1.2
Clasificación de materiales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
2.1
coeficientes α (temperatura de resistividad) para distintos metales. . . . . . 118
2.2
Materiales superconductores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
3.1
Valores de campo magnético de distintos materiales . . . . . . . . . . . . . . 153
5.1
Constantes dieléctricas de varios materiales . . . . . . . . . . . . . . . . . . . 254
5.2
Susceptibilidades magnéticas para algunas sustancias diamagnéticas y
paramagnéticas a 300 K . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268
xxiii
xxiv
Índice de cuadros
Capítulo 1
Electrostática
l rayo es una poderosa descarga eléctrica natural, producida durante un tormenta
eléctrica. La descarga precipitada del rayo es acompañada por la emisión de luz
(el relámpago), causada por el paso de corriente eléctrica que ioniza las moléculas de
aire. La electricidad que pasa a través de la atmósfera calienta y expande rápidamente
el aire, produciendo el ruido característico del rayo; el trueno.
E
1.1.
Introducción
ué interés tiene el estudio del electromagnetismo?. En esta introducción,
entregaremos una idea preliminar del porqué de la importancia de este campo
de la física.
¿Q
1.1.1.
La interacción electromagnética
Según la clasificación actual, existen en la naturaleza cuatro interacciones fundamentales: nuclear fuerte, electromagnética, nuclear débil y gravitacional (en orden de
decreciente intensidad ).
Interacción Nuclear Fuerte Mantiene unidos a los nucleones (protón y neutrón),
venciendo la repulsión electromagnética entre los protones que poseen carga
eléctrica del mismo signo. Esta interacción es de corto alcance (1x10−15 [m] ≈ 1[f m]).
2
1.1. Introducción
Interacción Electromagnética Interacción entre las partículas con carga eléctrica. Es una
interacción de largo alcance.
Interacción Nuclear Débil En el modelo estándar de la física de partículas, se debe
al intercambio de los bosones w y z. Es responsable del decaimiento β y la
radioactividad. Esta interacción es 1013 veces menor que la nuclear fuerte.
Interacción Gravitacional Interacción que experimentan los objetos con masa. Sus
efectos se hacen sentir principalmente en la escala astronómica.
El electromagnetismo es simplemente otra interacción fundamental, mucho más importante que la gravitación dentro del rango de lo cotidiano. Las fuerzas electromagnéticas
son responsables de la estructura de la materia y de casi la totalidad de los fenómenos
físicos y químicos que intervienen en nuestra vida diaria. Eso no quiere decir que sus
efectos pueden ser siempre explicados por la física clásica. En todo aquello que depende
de la escala atómica es preciso emplear la física cuántica.
Aún desde un punto de vista fundamental, la interacción electromagnética es aquella
que comprendemos mejor. Su tratamiento teórico, a nivel cuántico (electrodinámica
cuántica), sirve hoy en día como modelo para el tratamiento de todas las interacciones
conocidas restantes. En el desarrollo de la física, la teoría clásica de interacción
electromagnética, formulada por James Clerck Maxwell, desempeñó un papel central, como
prototipo de una teoría de campo. Además, sirvió como puente para la elaboración de la
teoría de la relatividad. Para esto, fue necesario modificar la propia mecánica newtoniana,
mas la teoría de James Clerck Maxwell permaneció intacta. Así, la teoría de interacción
electromagnética desempeñó un papel central, ya que permitió obtener una de las grandes
síntesis de la ciencia, la unificación del electromagnetismo y la óptica, mostrando que la
luz es una onda electromagnética.
Las aplicaciones del electromagnetismo revolucionaron toda la tecnología. La
industria, iluminación, transportes, computación, entretenimiento, funcionan a base de
la energía eléctrica. Las ondas electromagnéticas (radio, radar, televisión) son empleadas
en todos nuestros sistemas de comunicación. En resumen, el electromagnetismo es una
disciplina básica y fundamental tanto desde un punto de vista teórico como práctico.
1.1. Introducción
1.1.2.
3
Historia
La palabra electromagnetismo es de origen griego y se divide en dos partes; Electrón
(ámbar) que significa eléctrico y Magnesia, provincia de Grecia que posteriormente derivó
a la palabra magnético.
Figura 1.1: Mapa de Grecia que muestra la ubicación de Magnesia.[1]
Existen diversos registros a través de la historia que dan cuenta de las observaciones
fenomenológicas de los materiales magnéticos:
2000 a.c. Documentos de la antigua China sugieren que el magnetismo ya había sido
observado.
700 a.c. Primeras observaciones de la atracción eléctrica realizada por los antiguos
griegos. Estos observaron que al frotar el ámbar, éste atraía pequeños objetos como
pajitas o plumas.
1600 William Gilbert, médico de la corte de Inglaterra, publicó su tratado De Magnete,
donde menciona que la electrificación no es una propiedad exclusiva del ámbar, sino que
más bien es un fenómeno de tipo general.
1600-1729 Científicos electrificaron una gran variedad de objetos.
1.1. Introducción
4
1729 Stephan Gray descubrió que las cargas eléctricas pueden ser transmitidas a
través de ciertos materiales, llamados conductores. Las conclusiones de sus experiencias
señalan que:
Existen dos tipos de cargas.
Cargas similares se repelen.
Cargas diferentes de atraen.
1706-1790 Benjamin Franklin denominó positivas a las cargas que aparecen en el
vidrio y negativas a las que aparecen en la goma (caucho). Franklin formuló la teoría de
que estos fenómenos se producen debido a la existencia de un fluído eléctrico que se
transfiere de un cuerpo a otro. El frotamiento sería la causa de la transferencia:
El cuerpo que recibiera más fluido quedaría electrizado positivamente.
El cuerpo que perdiera más fluido quedaría electrizado negativamente.
(a) Fuerza de atracción
(b) Fuerza de repulsión
Figura 1.2: Experimento entre una barra de caucho y una de vidrio, que
demuestra que existe una fuerza de atracción y/o de repulsión entre
sistemas cargados.
1.1. Introducción
5
De esta manera, no habría ni creación ni destrucción de carga eléctrica, sino que
únicamente transferencia de electricidad de un cuerpo a otro.
1785 Charles Coulomb encontró la ley que expresa la fuerza que aparece entre cargas
eléctricas.
Hasta el fin del siglo XVIII, la electricidad y el magnetismo eran poco más que
curiosidades de laboratorio, sin una relación conocida entre ellas. En ambos casos sólo se
conocían efectos estáticos. En ese entonces se acababa de inventar la pila voltáica (1800)
y se conocían algunos de los efectos producidos por las corrientes eléctricas. Fue sólo a
principios del siglo XIX que se descubrieron los efectos magnéticos de las corrientes.
1819 Hans Oersted descubrió que la aguja de la brújula se desvía si se coloca cerca
de un circuito por el que pasa una corriente eléctrica. Así nació el electromagnetismo.
1831 Michael Faraday y Joseph Henry demostraron que cuando un imán se mueve
cerca de un alambre, se establece una corriente eléctrica en dicho alambre. Este efecto
se conoce como inducción electromagnética. Además, Fadaray introdujo el concepto de
campo eléctrico.
1873 James Clerck Maxwell aprovechó estas observaciones junto con otros experimentos como base para formular las leyes fundamentales del electromagnetismo.
1888 Heinrich Hertz comprobó las predicciones de Maxwell al producir ondas
electromagnéticas en su laboratorio. Este logro hizo posible desarrollos prácticos como
la radio y la televisión.
1909 Robert Millikan descubrió que las cargas eléctricas se presentan como algún
múltiplo entero de una cantidad básica de carga, e. Actualmente se dice que la carga está
cuantizada, siendo q el símbolo estándar usado como variable para la carga. La carga
eléctrica existe en forma de paquetes discretos, donde q = Ne, con N algún número
entero.
1910-1920 Otros experimentos demostraron que el electrón tiene una carga −e y
el protón una carga de igual magnitud, pero de signo contrario, +e. Algunas partículas
como el neutrón no poseen carga.
1.2. Propiedades de la carga eléctrica
6
1.2.
Propiedades de la carga eléctrica
1.2.1.
Dualidad de la carga
Todas las partículas cargadas pueden dividirse en positivas y negativas, de forma que
las de un mismo signo se repelen mientras que las de signo contrario se atraen.
(a) Fuerza de repulsión
(b) Fuerza de atracción
Figura 1.3: Fuerza de interacción entre dos cargas eléctricas.
1.2.2.
Conservación de la carga
En cualquier proceso físico, la carga total de un sistema aislado se conserva. Es
decir, la suma algebraica de cargas positivas y negativas en cierto instante no varía. Por
ejemplo, una caja de paredes delgadas, situada en el vacío, expuesta a rayos gamma,
podría ser el escenario de la creación de un par en el cual un fotón de alta energía
termina su existencia con la creación de un electrón negativo y uno positivo. Se han
creado dos partículas cargadas eléctricamente, pero la variación de la carga total dentro
de la caja es nula.
1.2. Propiedades de la carga eléctrica
7
Figura 1.4: Experimento que explica el Principio de Conservación de
la Carga.
1.2.3.
Cuantización de la carga
La carga eléctrica siempre se presenta como un múltiplo entero de una carga
fundamental, que es la del electrón. Cuando postulamos distribuciones continuas de carga
podemos considerarlas como valores medios de un gran número de cargas elementales,
de la misma forma que podemos definir la densidad macroscópica de un líquido, a pesar
de su discontinuidad a escala molecular.
En los cuerpos mucho mayores que las gotas de aceite de Millikan (radio del orden
de 1 (mm) ), la cuantización de la carga no es apreciable.
La unidad de carga en el Sistema Internacional (SI) es el Culombio (C), definido como
la cantidad de carga que fluye a través de un cable conductor en un segundo cuando la
intensidad de corriente en el mismo es de un Amperio.
Partícula
Carga [C]
Masa [Kg]
Electrón (e)
−1, 602181 · 10−19
9, 1095 · 10−31
Protón (p)
+1, 602181 · 10−19
1, 672661 · 10−27
Neutrón (n)
0
1, 67492 · 10−27
Cuadro 1.1: Valores de carga y masa para los componentes del átomo.
1.3. Ley de Coulomb
8
1.2.4.
Carga por inducción
Supongamos una esfera neutra, con igual cantidad de cargas positivas y negativas.
Al acercársele una varilla de caucho cargada, los electrones sobre la esfera neutra se
redistribuyen. Al conectar la esfera a tierra, algunos electrones se fugan a través del
alambre a tierra. Al eliminar la conexión a tierra, la esfera queda con demasiada carga
positiva que no está distribuida de manera uniforme. Al retirar la varilla, los electrones
restantes se redistribuyen y se tiene una distribución uniforme positiva neta sobre la
esfera.
Figura 1.5: Inducción de carga sobre una esfera conductora.
1.3.
Ley de Coulomb
n electrostática, consideraremos solamente configuraciones de cargas en reposo, es
decir, en equilibrio estático: no hay variación con el tiempo. La fuerza ejercida por
una carga sobre otra fue estudiada por Charles Coulomb en 1785 mediante una balanza
de torsión de su propia invención.
E
1.3. Ley de Coulomb
9
Figura 1.6: Balanza de torsión de Coulomb.
La fuerza eléctrica entre las esferas A y B provoca que las esferas se atraigan o
se repelan una a la otra, y el movimiento resultante provoca que la fibra suspendida
se tuerza. De este modo, la fuerza de interacción se calcula en términos del ángulo de
rotación de la fibra. El resultado obtenido por Coulomb se resume en
q1 q2
q1 q2
F~12 = ke 2 r̂ = ke 3 ~r.
r
r
(1.1)
Aquí q1 y q2 son numeros (escalares) que dan el valor y signo de las cargas
respectivas, ~r es el vector unitario en la dirección de la carga 1 a la carga 2, y F~12
es la fuerza ejercida por la carga q1 sobre la carga q2 . En este caso hemos usado cargas
puntiformes, ya que estamos suponiendo que la dimension de los cuerpos cargados es
despreciable con respecto a la distancia entre ellos. La restricción a cargas estacionarias
se ha hecho, de momento, para excluir las fuerzas originadas por las cargas móviles, que
estudiaremos más adelante.
1.3. Ley de Coulomb
10
De la ecuación (1.1), que la fuerza es proporcional al producto de las cargas e
inversamente proporcional al cuadrado de la distancia entre ellas. La dependencia inversa
con el cuadrado de la distancia puede ser verificada variando la distancia entre las cargas.
En los experimentos de Coulomb, la precisión no era muy buena (2 + ε) con ε < 0, 02. Sin
embargo, E. R. Williams y colaboradores demostraron en 1971 que (2+ε) con ε < 3·10−16 .
En el sistema de unidades CGS, que adopta los centímetros, gramos y segundos
como unidades básicas, ke = 1 para interacciones entre cargas en el vacío, y se define la
unidad de carga como aquella que ejerce una fuerza de 1 [dina] sobre otra carga idéntica
a una distancia de 1 [cm]. Este sistema es usualmente empleado en física atómica. Sin
embargo, las unidades definidas en esta forma son muy pequeñas para aplicaciones
prácticas, particularmente en la ingeniería. Vamos a adoptar el sistema más empleado
para las aplicaciones prácticas del electromagnetismo, el Sistema internacional (SI) o
MKS, basado en metros, kilogramos y segundos. En este sistema, la constante de Coulomb
se define como
2
2
1
−7 2 N · m
9 N ·m
= 10 c
≈ 8, 98755 · 10
,
(1.2)
ke ≡
4πε0
C2
C2
donde c es la velocidad de la luz en el vacío, actualmente definida como 299792458 [m/s].
La constante ε0 se denomina la permitividad del espacio libre.
1.3.1.
Comparación entre la fuerza de gravitación y la fuerza eléctrica
La fuerza eléctrica y la fuerza de gravitación, junto con las fuerzas nucleares (Fuerte
y Débil) son básicas en nuestro universo y sólo rigen a distinta escala. Hay una gran
semejanza en la estructura matemática de la Ley de Coulomb y la Ley de Gravitación
Universal de Newton
Ley de Coulomb
−→
q1 q2
F12 = ke 2 r̂
r
ke = 8, 98755 ·
109
N · m2
C2
Ley de Gravitación universal
−→
m1 m2
F12 = −G 2 r̂
r
G = 6, 67 ·
10−11
N · m2
K g2
1.3. Ley de Coulomb
11
Ambas son leyes que dependen de la inversa del cuadrado de la distancia.
La Fuerza Gravitatoria es proporcional a las masas y atractiva.
La Fuerza Eléctrica es proporcional a las cargas y puede ser atractiva o repulsiva.
1.3.1.1.
Ejemplo
Calcular la relación que existe entre las fuerzas eléctrica y gravitatoria ejercidas entre
el protón y el electrón de un átomo de hidrógeno.
solución
e2
r2
mp me
Fg = G 2
r
ke2
Fe
=
Fg
Gmp me
Fe = k
=
Nm2
)(1, 6 · 10−19 [C ])2
C2
(8, 98 ·
NM 2
−11
6, 67 · 10
(1, 76 · 10−27 [K g])(9, 11 · 10−31 )[K g]
K g2
109
≈ 1040
1.3.2.
Principio de superposición
Sea cual fuere el número de cargas presentes en nuestro sistema, la ley de
Coulomb puede utilizarse para calcular la interacción de cada par. Esto es la base del
principio de superposición el cual invocaremos muchas veces en nuestro estudio del
electromagnetismo. En un sistema de cargas, cada una de ellas ejerce una fuerza sobre
cada una de las restantes.
1.3. Ley de Coulomb
12
Figura 1.7: Principio de superposición de la fuerza de Coulomb.
Así, la fuerza neta sobre cada carga es la suma vectorial de las fuerzas individuales
ejercidas sobre dicha carga i-ésima por las cargas restantes del sistema
F~1 = F~21 + F~31 + F~41 ,
esto es una consecuencia del principio de superposición de las fuerzas
X qj
r̂j,i .
F~i = ke qi
r2
j6=i j,i
1.3.2.1.
(1.3)
(1.4)
Ejemplo
Dos protones en una molécula de hidrógeno están separados por una distancia de
0, 74 · 10−10 (m). Calcule la fuerza eléctrica que ejerce un protón sobre el otro.
Solución
F =k
q1 q2
r2 "
= 9 · 109
#
2 (1, 6 · 10−19 [C ])(1, 6 · 10−19 [C ])
N
m
2
(0, 74 · 10−10 [
m])2
C
= 42, 07 · 10−9 [N]
1.3.2.2.
Ejemplo
Tres cargas puntuales, q1 = −3, 1 [µC ], q2 = 1, 2 [µC ], y q3 = 5 [µC ], se colocan como
se muestra en la figura 1.8. Determine la fuerza resultante sobre q3 .
1.3. Ley de Coulomb
13
Figura 1.8: ejercicio para tres cargá puntuales en dos dimensiones.
solución
F~3 = k
2
X
F~i3
i=1
=k
2
X
q1 q3
i=1
=k
3
ri3
~ri3
q1 q3
q2 q3
~r13 + 3 ~r23
3
r13
r23
= 0, 051ı̂ + 0, 549̂
donde hemos usado que:
~r13 = ~r3 − ~r1
= (0, 3 [m])ı̂ − (0, 3 [m])̂
q
~r13 | = (0, 3 [m])2 + (0, 3 [m])2
= 0, 424 [m]
~r23 = ~r3 − ~r2
= (0, 3 [m])ı̂
= 0, 3 [m]
1.3.3.
Energía de un sistema de cargas
Consideremos el trabajo que debemos cederle al sistema para llevar cuerpos cargados
a una posición en particular. Comenzaremos con dos partículas cargadas (q1 y q2 ) muy
1.3. Ley de Coulomb
14
distantes la una de la otra, luego Acercaremos lentamente las partículas hasta que su
distancia sea r12 . ¿Cuál fue el trabajo requerido?. En cualquier caso, el trabajo realizado
es la integral del producto fuerza por desplazamiento en la dirección de la fuerza. La
fuerza que se ha de aplicar para mover una carga hacia la otra es igual y de signo
contrario a la fuerza coulombiana:
Z
Z
r12
~
fuerza × distancia =
F~2 · ds
∞
Z r12
q1 q2
q1 q2
(−dr) = ke
W2 = ke
2
r12
r
∞
W2 =
(1.5)
(1.6)
Figura 1.9: Sistema de dos cargas que se acercan desde el infinito.
Debido a que r varia desde ∞ a r12 , el incremento de desplazamiento es −dr.
Sabemos que el trabajo realizado sobre el sistema debe ser positivo para cargas del
mismo signo. Vamos ahora a acercar una tercera carga q3 desde el infinito hasta un
punto P3 a una distancia r31 de la carga 1 y r32 de la carga 2. El trabajo requerido para
ello será:
1.3. Ley de Coulomb
15
Figura 1.10: Sistema de tres cargas que se acercan desde el infinito.
Z P2
Z P2
~ =
~ +
~
(F~13 + F~23 ) · ds
F~13 · ds
F~23 · ds
∞
∞
∞
∞
Z r12
Z r12
q1 q3
q2 q3
w 3 = ke
(−dr) + ke
(−dr)
2
r
r2
∞
∞
q1 q3
q2 q3
w 3 = ke
+ ke
r13
r23
Z
w3 =
P2
~ =
F~3 · ds
Z
P2
(1.7)
(1.8)
(1.9)
así, el trabajo total para reunir las tres cargas puntuales es la energía potencial
electrostática U del sistema de las tres cargas
U = ke
q1 q3
q2 q3
q1 q2
+ ke
+ ke
,
r12
r13
r23
(1.10)
Esta cantidad de trabajo es independiente del orden en el cual las cargas se
transportan hasta alcanzar sus posiciones finales. En este caso, hemos elegido como
cero de energía potencial la correspondiente a la situación en que las tres cargas, ya
existentes, se encuentran infinitamente separadas unas de otras.
En general, la energía potencial electrostática de un sistema de cargas puntuales es
el trabajo necesario para transportar las cargas desde una distancia infinita hasta sus
posiciones finales.
Este resultado puede generalizarse a cualquier número de cargas. Si tenemos N
1.3. Ley de Coulomb
16
cargas distintas, en una distribución arbitraria en el espacio, la energía potencial del
sistema se calcula sumando todos los productos binarios de cargas.
1.3.3.1.
Ejemplo
Calcularemos la energía potencial de una distribución de ocho cargas negativas (−e)
en los vértices de un cubo de arista b, con una carga positiva (+2e) en el centro del cubo.
Figura 1.11: Ejercicio para un cubo hecho de cargas.
Solución
U = 12k
(−e)(−e)
(−e)(+2e)
(−e)(−e)
(−e)(−e)
+ 12k √
+ 8k √
+ 4k √
b
3/2(b)
2b
3b
12ke2 12ke2
16ke2
4ke2
+ √
−√
+√
b
3/2b
2b
3b
kee
12
32
4
12 + √ − √ − √
=
b
2
3
3
=
U=
4, 32e2
b
Para que los electrones escapasen de esta configuración, la energía cinética total de las
partículas tendría que ser U. Una manera de escribir la suma de los productos binarios
es
N
N
1 X X qi qj
U=
,
2
rij
i=1 j6=i
debido a que el producto binario aparece dos veces, hemos multiplicado por 1/2.
1.4. Campo eléctrico
1.4.
17
Campo eléctrico
n escalar es una cantidad determinada completamente por su magnitud. Un vector es
una cantidad que se determina completamente por su magnitud, dirección y sentido.
U
El concepto de campo es de gran importancia en ciencia, particularmente en física. La
idea es atribuirle propiedades al espacio, en vez de considerar a los verdaderos causales
de los fenómenos que ocurren en dicho espacio. Para comprender esto, veamos algunos
ejemplos
Campo de Temperaturas El campo de temperaturas es un campo escalar. La intensidad
del campo en un punto arbitrario P corresponde a lo que mide el termómetro en
ese punto. Es una magnitud escalar puesto que no posee dirección asociada. La
verdadera causa de que la temperatura en ese punto sea un valor x es la estufa,
la puerta, la temperatura exterior, etc. Evidentemente no depende del instrumento
con que se mide la intensidad del campo de temperaturas, es decir, no depende del
termómetro.
Figura 1.12: Líneas de Campo de temperatura.
Campo de velocidades : El campo de velocidades es un campo vectorial. En cada
dirección de un rio, el agua se mueve con una velocidad específica (magnitud,
dirección y sentido).
1.4. Campo eléctrico
18
Figura 1.13: Campo de velocidades.
Campo gravitacional El campo gravitacional es un campo vectorial.
Figura 1.14: Representación del campo gravitacional generado por la
Tierra.
Supongamos que tenemos una distribución de cargas q1 , q2 , . . . , qN , fijas en el espacio,
y nos interesa, no las fuerzas que se ejercen mutuamente, sino su efecto sobre otra carga
q0 que puede situarse en sus proximidades. Sabemos cómo determinar la fuerza resultante
sobre esta carga dada su posición
F~0 =
N
X
i=1
N
X qi
q0 qi
ke 2 r̂i,0 = ke q0
r̂i,0 .
ri,0
r2
i=1 i,0
(1.11)
1.4. Campo eléctrico
19
La fuerza es proporcional a q0 , así que si dividimos por esta carga obtenemos una
magnitud que depende sólo de las cargas originarias. A esta función se le conoce como
campo eléctrico
N
X
~
qi
~ = F0 = ke
E
r̂ .
2 i,0
q0
ri,0
(1.12)
i=1
(a) especificar1
(b) especificar2
Figura 1.15: ejemplo-campo-eléctrico.
Hasta aquí no tenemos nada nuevo. El campo eléctrico es simplemente otra manera
de describir el sistema de cargas; nos entrega la fuerza por unidad de carga, en módulo
y dirección, que una carga de prueba q0 experimentaría en cada punto del espacio.
Sin embargo, el campo eléctrico asigna a cada punto en un sistema una propiedad
~ en una alguna región del espacio, sabemos lo que
local en este sentido: si conocemos E
le ocurrirá a cualquier carga en aquella región. No necesitamos conocer lo que produce
el campo. Si conocemos el campo eléctrico en todos los puntos del espacio, tenemos una
descripción completa de todo el sistema, que revelará las posiciones y valores de todas
las cargas.
1.4.0.2.
Ejemplo
Un protón experimenta una fuerza eléctrica de 3 · 10−17 ı̂ [N], en un cierto punto P del
espacio. Encuentre el valor del campo eléctrico en este punto.
1.4. Campo eléctrico
20
Solución
~
~=F
E
q
3 ·−17 [N]
ı̂
1, 6 · 10−19 [C ]
N
= 187, 5
ı̂
C
=
1.4.0.3.
Ejemplo
¿Cuál es la magnitud y dirección del campo eléctrico que compensa el peso de (a) un
electrón y (b) un protón?
Solución
~ = 0. El campo eléctrico está dado por
Del diagrama de cuerpo libre tenemos F~ + W
~
~ y el peso de una partícula es W
~ 0 − mg̂. De esta manera tenemos que:
~ = F → F~ = qE
E
q
~ − mg̂ = 0
qE
~ = mg ̂
→E
q
y para los valores, tenemos:
(a) q = −1, 6 · 10−19 [C ], m = 9, 1 · 10−31 [K g], g = 9, 81 [m/s2 ]
~ = −5, 58 · 10−11 [N/C ]̂
E
(b) q = +1, 6 · 10−19 [C ], m = 1, 67 · 10−27 [K g], g = 9, 81 [m/s2 ]
~ = 1, 024 · 10−7 [N/C ]̂
E
1.4.1.
Líneas de campo eléctrico
Las líneas de campo son aquellas cuyas tangentes, en cualquier punto, tienen la
dirección del campo en este punto. Tales líneas son curvas continuas exceptuando en las
singularidades tales como las cargas puntiformes, o en aquellos puntos donde el campo
eléctrico es nulo.
1.4. Campo eléctrico
21
El dibujo de una línea de campo no entrega directamente el valor del campo, aunque
de manera general, el número de líneas por unidad de superficie que pasan a través de
un área perpendicular a dichas líneas es proporcional a la magnitud del campo eléctrico
en dicha región. Es decir, las líneas convergen cuando nos aproximamos a una región de
campo intenso, y se separan al aproximarnos a una región de campo débil.
Las reglas para dibujar las líneas de campo son:
Las líneas deben empezar en una carga positiva y terminar en una carga negativa.
En el caso de que haya un exceso de cargas, algunas líneas terminarán en el
infinito.
El número de líneas dibujadas saliendo de una carga positiva o acercándose a una
carga negativa es proporcional a la magnitud de dichas cargas.
No es posible que las líneas de campo se crucen.
Figura 1.16: Líneas de Campo Eléctrico
1.4.2.
Movimiento de cargas puntuales en campos eléctricos
~ ésta
Cuando una partícula con carga q y masa m se coloca en un campo eléctrico E,
experimenta la acción de una fuerza
~ = m~
F~ = qE
a,
(1.13)
1.4. Campo eléctrico
22
de este modo, la partícula adquiere una aceleración. Con frecuencia, la velocidad de un
electrón en un campo eléctrico es una fracción importante de la velocidad de la luz; en
este caso, las leyes de Newton del movimiento deben sustituirse por la Teoría especial
de la relatividad de Einstein.
1.4.2.1.
Ejemplo
El campo eléctrico en la región entre dos placas metálicas con cargas opuestas es
aproximadamente uniforme. Suponga que desde el origen se proyecta horizontalmente
un electrón al interior de este campo con una velocidad inicial vi ı̂ en un tiempo t = 0[s].
Calcule la trayectoria del electrón.
Figura 1.17: Carga eléctrica en movimiento en presencia de un campo
eléctrico uniforme.
Solución
Las ecuaciones de movimiento son
1
x : x0 + v0x t + ax t 2 = vi t
2
1
1
y : y0 + v0y t + ay t 2 = ay t 2
2
2
1.4. Campo eléctrico
23
Por otro lado la fuerza está dada por
~ = m~
F~ = qE
a
q~
~= E
⇒a
m
(−e)E
~=
a
̂
m
De esta forma tendremos que

1 (−e)E 2 
t 
y=
eE 2
2 m
x  → y = − 2mv 2 x .
i
x = vi t ⇒ t = 
vi
En consecuencia, la trayectoria es una parábola.
1.4.3.
Distribuciones continuas de cargas
A escala microscópica, la carga eléctrica está cuantizada. Sin embargo, con frecuencia
se presentan situaciones en las que un gran número de cargas están tan próximas que
la carga total puede considerarse distribuida continuamente en el espacio.
Figura 1.18: Distribución continua de la carga.
El campo eléctrico en el punto P debido a un elemento de carga ∆q es
~ = ke
∆E
∆q
r̂,
r2
(1.14)
1.4. Campo eléctrico
24
de esta manera, el campo eléctrico total en el punto P debido a todos los elementos en
la distribución de carga es
~ = ke
E
X ∆qi
i
ri2
r̂.
(1.15)
Como la distribución de carga ha sido modelada como continua, entonces
~ = ke lı́m
E
∆qi →0
X ∆qi
i
ri2
Z
r̂i = ke
dq
r̂.
r2
(1.16)
Si una carga Q se encuentra distribuida de manera uniforme en un volumen V , la
densidad de carga volumétrica se define como
ρ≡
Q
dq
=
.
V
dV
(1.17)
Si una carga Q se encuentra distribuida de manera uniforme sobre una superficie de
área A, la densidad de carga superficial se define como
σ≡
Q
dq
=
.
A
dA
(1.18)
Si una carga Q se encuentra distribuida de manera uniforme a lo largo de una línea
de longitud L, la densidad de carga lineal se define como
λ≡
1.4.3.1.
Q
dq
=
.
L
dL
(1.19)
Ejemplo
Una varilla de longitud L tiene una carga positiva uniforme por unidad de longitud λ
y una carga total Q. Calcule el campo eléctrico en un punto P ubicado a lo largo del eje
principal de la varilla y a una distancia a de uno de sus extremos.
1.4. Campo eléctrico
25
Figura 1.19: Línea de carga continua.
Solución
Debido a que la varilla tiene una carga λ por unidad de longitud, la carga dq tiene
~ en P debido a este
un valor sobre el segmento pequeño de dq = λdx. El campo dE
segmento está en la dirección negativa de las x, y su magnitud es
dq
x2
dx
dE = kλ 2
x
dE = k
Z
E = kλ
a+L
a
dx
x2
1 a+L
E = kλ −
x a
1
1
kλL
E = kλ −
+
=
a+L a
a(a + L)
como Q = λL entonces
E=
kQ
.
a(a + L)
1.4. Campo eléctrico
26
1.4.3.2.
Ejemplo
Un anillo de radio a tiene una carga total Q positiva distribuida de manera uniforme.
Calcule el campo eléctrico generado por el anillo en un punto P a una distancia x de su
centro y a lo largo del eje central perpendicular al plano del anillo.
Figura 1.20: Anillo uniformemente cargado de radio a, el campo en P
sobre el eje x es debido aun elemento de carga ∆q.
solución
Es importante observar que las componentes en y se anulan de a pares. Es por ello
que sólo calcularemos la componente en x:
dEx = k
dq
cos θ
r2
1.4. Campo eléctrico
pero r =
√
x 2 + a2 y cos θ =
27
x
r
=
√ x
x 2 +a2
dEx =
de modo que
(x 2
kxdq
+ a2 )3/2
Z
kxdq
+ a2 )3/2
Z
kx
Ex = 2
dq
(x + a2 )3/2
kQx
Ex = 2
(x + a2 )3/2
Ex =
1.4.3.3.
(x 2
Ejemplo
Un disco de radio R tiene una densidad de carga superficial uniforme σ . Calcule el
campo eléctrico en un punto P que está sobre el eje perpendicular al centro del disco, y
a una distancia x del centro del mismo.
Figura 1.21: Disco uniformemente cargado de radio R.
Consideremos un anillo de radio r y ancho dr. De esta forma tendremos que
dq = σ dA = 2πσ rdr donde dA = 2πrdr es el área del anillo.
Resolviendo de la misma forma que en el ejemplo anterior tendremos
1.5. Ley de Gauss
28
dEx = k
dq
dq x
cos θ = k 2
2
t
t t
kdqx
= 2
(x + r 2 )3/2
2kxπσ rdr
= 2
(x + r 2 )3/2
y el campo total será
Z
Ex = kxπσ
0
R
(x 2
2rdr
+ r 2 )3/2
Realizando el cambio de variable µ = x 2 + r 2 , dµ = 2rdr entonces:
Z
x 2 +r 2
dµ
µ 3/2
x2
−1/2 x 2 +r 2
µ
Ex = kxπσ
−1/2 x 2
x
Ex = 2πkσ 1 − √
x2 + R2
Ex = kxπσ
1.5.
Ley de Gauss
s un procedimiento alternativo para calcular los campos eléctricos debidos a
distribuciones de carga. La ley de Gauss es una de las ecuaciones de Maxwell, las
ecuaciones fundamentales del electromagnetismo. La ley de Gauss y la Ley de Coulomb
son equivalentes. Esta ley permite calcular fácilmente los campos eléctricos que resultan
de distribuciones simétricas de carga.
E
1.5.1.
Flujo
Consideremos cierto campo eléctrico en el espacio, y en éste cierta superficie cerrada
arbitraria. Dividimos la superficie en pequeños segmentos, los cuales son tan pequeños
que en cada uno de ellos la superficie es prácticamente plana y el vector campo no varía
apreciablemente de un punto a otro del segmento.
1.5. Ley de Gauss
29
~ La
Figura 1.22: Superficie arbitraria inmersa en un campo eléctrico E.
superficie se divide en pequeños segmentos de superficie de área ∆Ai .
Representamos la normal a la superficie como un vector. Para cada uno de los
segmentos en que se ha dividido la superficie, por ejemplo el segmento i, tenemos un
~ i que da su área y su orientación. Sea E
~i el vector campo eléctrico en la posición
vector ∆A
del segmento i. Entonces, el flujo a través de este segmento está dado por
~ i · ∆A
~i
∆φ = E
= Ei ∆Ai cos θ.
(1.20)
(1.21)
Para comprender el origen del nombre, imaginemos una función vectorial que
represente la velocidad del movimiento del aire, donde la velocidad varía de un lugar
a otro, pero es constante con el tiempo en una posición determinada. Denotemos este
campo vectorial por v~.
1.5. Ley de Gauss
30
Figura 1.23: Líneas de fuerzas correspondientes a un campo eléctrico
uniforme perpendicular al área A, pero que forma un ángulo θ con el
vector de unidad n̂ normal al área A0 .
~ es el área orientada de una hoja de papel, entonces el flujo de aire por unidad
Si A
de tiempo es
~
φ = ν~ · A.
(1.22)
Debemos señalar que nuestra definición de flujo puede aplicarse a cualquier función
vectorial, como por ejemplo, a la velocidad de la corriente de un río.
Retomando, sumemos el flujo a través de todos los segmentos para obtener el flujo a
través de la superficie total
X
~ i · ∆A
~i.
φ=
E
(1.23)
i
En el límite en que los segmentos son cada vez más pequeños, pasamos de una
sumatoria a la integral de superficie
Z
~ · dA.
~
φ= E
(1.24)
s
El flujo neto a través de una superficie cerrada viene dada por
I
I
~
~
φ = E · dA = En dA,
s
s
(1.25)
así el flujo neto a través de la superficie es proporcional al número neto de líneas que
salen de la superficie.
φ ≈ (líneas que salen − líneas que ingresan).
(1.26)
1.5. Ley de Gauss
1.5.1.1.
31
Ejemplo
Considere un campo eléctrico uniforme orientado en la dirección x. Determine el flujo
eléctrico neto a través de la superficie de un cubo de arista l, orientado como se ilustra
en la figura.
Figura 1.24: Superficie en forma de cubo en un campo eléctrico
uniforme paralelo al eje x.
Solución
El flujo neto es la suma de los flujos que atraviesan todas las caras del cubo. Primero
hay que darse cuenta que el flujo a través de cuatro de las caras es cero, porque el campo
~ en estas caras es perpendicular a dA.
~
E
Z
Z1
~ · dA
~=
E
~ · dA
~=
E
2
Z
Z1
Z
EdA cos π = − EdA = −EA = −El2
Z1
EdA cos 0 = − EdA = −EA = El2
2
2
φ = −El + El = 0
2
1.5.2.
2
Ley de Gauss
La ley de Gauss es la relación entre el flujo eléctrico neto a través de una superficie
cerrada y la carga encerrada por la superficie.
1.5. Ley de Gauss
32
Supongamos un campo eléctrico generado por una sola carga puntual aislada positiva
q, localizada en el centro de una esfera de radio r. ¿Cuál es el flujo a través de esta esfera?.
Figura 1.25: Campo eléctrico generado por una carga puntual q,
localizada en una esfera de radio r.
El campo eléctrico en un punto cualquiera de la superficie es
~ = ke q r̂
E
r2
(1.27)
y su dirección y sentido es el mismo que el de la normal hacia el exterior en este punto,
entonces
I
I
I
I
~
~
φ = E · dA = EdA cos 0 = EdA = E dS,
(1.28)
s
s
s
s
además, como la superficie es esférica tenemos
I
s
Z
dA =
2π
Z
π
Z
r sin θdθdφ = r
2
0
2π
2
0
(− cos π + cos 0)dφ = 4πr 2
(1.29)
0
de manera que el flujo neto está dado por
I
φ=E
φ=
q
.
ε0
s
dA = ke
q
r2
2 = 4πke q
4π r
A continuación presentamos diferentes superficies que rodean la carga q.
(1.30)
(1.31)
1.5. Ley de Gauss
33
Figura 1.26: Superficies cerradas de varias formas, circundando una
carga q.
El flujo eléctrico neto es el mismo a través de todas las superficies, porque el mismo
número de líneas de campo las cruzan.
En conclusión, podemos decir que: El flujo neto a través de cualquier superficie
cerrada que rodea a una carga puntual q tiene un valor q/ε0 y es independiente de
la forma de la superficie.
En el caso en que tengamos una carga puntual fuera de la superficie cerrada, el
número de líneas que entran en la superficie es el mismo que el número de líneas que
salen. Por lo tanto, podemos concluir que el flujo eléctrico neto a través de una superficie
cerrada que no rodea a ninguna carga es igual a cero.
1.5. Ley de Gauss
34
Figura 1.27: Carga puntual localizada afuera de una superficie cerrada,
donde las líneas que entran es igual al número que salen de ella.
1.5.3.
Principio de superposición
El campo eléctrico debido a muchas cargas es igual a la suma vectorial de los campos
eléctricos producidos por cada una de las cargas individuales. De esta forma el flujo total
debido a un conjunto de cargas será:
I
φ=
1.5.3.1.
s
~ · dA
~=
E
Z
s
~1 + E
~2 + . . . E
~N ] · dA.
~
[E
Ejemplo
Calcule el flujo en cada superficie cerrada.
(1.32)
1.5. Ley de Gauss
35
Figura 1.28: Distintas superficies cerrando cargas q1 , q2 y q3 .
Solución
El flujo en cada superficie será
q1
ε0
q2 + q3
φs0 =
ε0
φs =
φ200 = 0
~ a través de una superficie cerrada
Finalmente tenemos que el flujo del campo eléctrico E
~ · dA
~ extendida a la superficie, es igual a 1/ε0 por la
cualquiera, es decir, la integral E
carga total encerrada por la superficie.
I
~ · dA
~
φ= E
s
Z
1 X
1
ρdV
=
qi =
ε0 i
ε0 V
Es fácil ver que la ley de Gauss no se cumpliría si, por ejemplo, la ley de la fuerza fuese
inversa al cubo. En este caso, el flujo del campo eléctrico de una carga puntual q a través
de una esfera de radio R con el centro en la carga sería:
I
1 q 2
q
φ = E · dA = 4πR =
3
4πε0 R
ε0 R
s
De este modo, haciendo la esfera suficientemente grande, podemos hacer el flujo a través
de ella tan pequeño como queramos, mientras que la carga total en el interior permanezca
constante.
1.5. Ley de Gauss
36
1.5.4.
Campo eléctrico debido a una carga puntual
Figura 1.29: La carga q está en el centro de una superficie esférica
~ es paralelo a dA en cualquier punto sobre la
Gaussiana, donde E
superficie.
Nuestra superficie gaussiana es una superficie esférica, de modo que
I
φ=
s
~ · dA
~=E
E
I
s
q
ε0
~ = 1 q r̂.
E
4πε0 r 2
dA = E(4πr 2 ) =
~
=⇒ E es constante y paralelo a A
Hemos deducido la ley de Coulomb a partir de la ley de Gauss. Ambas leyes son
equivalentes para cargas estáticas.
1.5.4.1.
Ejemplo
Determinar el campo eléctrico (a) fuera y (b) dentro de una esfera sólida
uniformemente cargada de radio r portadora de una carga Q que está distribuida por
todo el volumen de la esfera con densidad de carga ρ = Q/V .
1.5. Ley de Gauss
(a) Campo eléctrico fuera
37
(b) Campo eléctrico dentro
Figura 1.30: Esfera aislante uniformemente cargada de radio a y carga
total Q.
(a) Campo eléctrico fuera de la esfera
I
I
~ · dS
~ = E dS
~ =E(4πr 2 ) = q
φ= E
ε0
s
s
~ = 1 Q r̂ = k Q r̂
E
4πε0 r 2
r2
(b) Campo eléctrico dentro de la esfera
I
I
qint
~
~
φ = E · dS = E dS =
ε0
s
s
ρV 0
⇒ E(4πr 2 ) =
· V /V
ε0
QV 0
E(4πr 2 ) =
ε0 V
4
3
Q
πr
Qr 3
3
E(4πr 2 ) =
=
ε0 R 3
ε0 34 πR 3
~ = 1 Qr r̂ = k Qr r̂
E
4πε0 R 3
R3
1.5.4.2.
Ejemplo
Determinar el campo eléctrico para (a) r > a y (b) r < a debido a un cascarón
esférico uniformemente cargado de radio a y carga neta Q.
1.5. Ley de Gauss
38
Figura 1.31: Cascarón esférico uniformemente cargado.
Solución
(a) Campo eléctrico para r > a
I
φ=
s
I
q
ε0
s
q
E(4πr 2 ) =
ε0
~ = 1 q r̂ = k q r̂
E
4πε0 r 2
r2
~ · dS
~ =E
E
dS =
(b) Campo eléctrico para r < a
I
φ=
s
~ · dS
~ =E
E
I
s
dS =
qint
ε0
E(4πr 2 ) = 0
E =0
1.5.4.3.
Ejemplo
Determinar el campo eléctrico a una distancia r desde una linea de carga positiva de
longitud infinita y carga constante por unidad de longitud λ.
1.5. Ley de Gauss
39
Figura 1.32: Línea infinita de carga positiva rodeada por una superficie
gaussiana cilíndrica concéntrica con la línea de carga.
Solución
Nuestra superficie gaussiana es una superficie cilíndrica
I
I
qint
~
~
φ = E · dS = E dS =
ε0
s
s
λL
ES =
ε0
El área de la superficie curva es S = 2πrL, de modo que
E(2πr L) =
~=
E
1.5.4.4.
λL
ε0
λ
λ
r̂ = 2k r̂
2πε0 r
r
Ejemplo
Determinar el campo eléctrico debido a un plano infinito no conductor de carga
positiva con densidad de carga superficial uniforme σ .
1.5. Ley de Gauss
40
Figura 1.33: Superficie gaussiana cilíndrica para el cálculo del campo
eléctrico, que penetra un plano infinito de carga positiva.
Solución
Nuestra superficie gaussiana es un cilindro. El flujo total es la suma de los flujos de
las tapas (iguales).
I
I
qint
~
~
φ = 2 E · dS = 2E ds =
ε0
s
s
σS
2E S
=
ε0
σ
E=
= 2πkσ
2ε0
1.5.5.
Divergencia de una función vectorial
~ en un punto P, a partir de su
Estamos interesados en calcular el campo eléctrico E
comportamiento en la vecindad inmediata a P.
La ley de Gauss
I
φ≡
s
~ · dS,
~
E
(1.33)
~ en el volumen
es un indicador global de la presencia de cargas (fuentes del campo E)
interno a la superficie S. Queremos ahora encontrar un indicador local que señale la
presencia de fuentes (cargas) en el punto P. Para esto envolvemos el punto P con una
1.5. Ley de Gauss
41
superficie gaussiana cerrada ∆Σ, que limita un volumen muy pequeño ∆V .
El volumen ∆V contiene una carga ∆q = ρ∆V , donde ρ es la densidad volumétrica
de carga. Aplicando la ley de Gauss a la superficie ∆Σ obtenemos
I
~ · dS
~ = ∆q = ρ∆V
φ∆Σ =
(1.34)
E
ε0
ε0
∆Σ
de manera que tendremos
lı́m
∆V →0
I
1
∆V
~ · dS
~ = ρ.
E
ε0
∆Σ
(1.35)
Este límite, que caracteriza la densidad de fuentes de campo en el punto P, es
independiente de la forma de la superficie ∆Σ y define así una característica local del
~ Esta característica local de campo recibe el nombre de divergencia
campo E.
I
1
~
~
~
~
E · dS ,
(1.36)
∇ · E ≡ lı́m
∆V →0 ∆V ∆Σ
de este modo obtenemos la forma local de la ley de Gauss,
~= ρ
~ ·E
∇
ε0
que corresponde a la primera ecuación de Maxwell.
(1.37)
1.5. Ley de Gauss
42
1.5.6.
Cálculo de la divergencia en coordenadas cartesianas
Para un vector cualquiera, ν~ , definimos
~ · ν~ ≡ lı́m
∇
∆V →0
I
1
∆V
~
ν~ · dS ,
(1.38)
∆Σ
~ es el elemento de
donde ∆V es un volumen arbitrario que envuelve a un punto P, y dS
~ · ν~ es
superficie orientado según la normal a la superficie ∆Σ de ∆V , de este modo, ∇
independiente de la forma del volumen ∆V . Vamos a escoger un elemento de volumen
con la forma de un paralelepípedo rectangular centrado en el punto P(x, y, z), y de lados
infinitesimales ∆x, ∆y, y ∆z.
Vamos a calcular el flujo de ν~ a través de las caras perpendiculares a la dirección x,
con área ∆y∆z, tomando los puntos 1 y 2, donde ν~ es calculado en el centro de estas
caras. Así, los puntos 1 y 2 tienen coordenadas (x ± ∆x/2, y, z) respectivamente, o sea,
sólo difieren por la coordenada x en ∆x.
El flujo φx , a través de estas dos caras, puede ser aproximado por
φx = [νx (2) − νx (1)]∆S = [νx (2) − νx (1)]∆y∆z.
(1.39)
Por la definición de derivada parcial, con ∆x infinitesimal, entonces
1
1 ∂νx (x, y, z)
∆x,
νx x ± ∆x, y, x = νx (x, y, z) ±
2
2
∂x
(1.40)
1.5. Ley de Gauss
43
de manera que
1 ∂νx (x, y, z)
∆x
2
∂x
1 ∂νx (x, y, z)
νx (1) = νx (x, y, z) −
∆x,
2
∂x
νx (2) = νx (x, y, z) +
por lo tanto
νx (2) − νx (1) =
(1.41)
(1.42)
∂νx (x, y, z)
δx
∂x
(1.43)
Sustituyendo en la ecuación (1.39) tenemos
φx = [νx (2) − νx (1)]∆y∆z =
∂νx
∂νx
∆x∆y∆z =
∆V
∂x
∂x
(1.44)
Para los flujos de las otras caras φy y φz , obtendremos resultados análogos
∂νy
∆V
∂y
∂νz
φz =
∆V ,
∂z
φy =
(1.45)
(1.46)
de modo que
I
φx + φy + φz =
~=
ν~ · dS
∆Σ
∂νy ∂νz
∂νx
+
+
∂x
∂y
∂z
∆V ,
(1.47)
donde ∆Σ es una superficie gaussiana que delimita al volumen ∆V .
Retomando la definición de divergencia, ecuación (1.38), finalmente tendremos que:
~ · ν~ ≡ lı́m
∇
∆V →0
∂νy ∂νz
∂νx
~
ν~ · dS =
+
+
,
∂x
∂y
∂z
∆Σ
I
1
∆V
(1.48)
donde las derivadas parciales son todas calculadas en el punto P(x, y, z).
Vamos ahora a definir la derivada parcial con respecto a x, de una función f (x, y, z),
escrita como ∂f /∂x, que significa la razón de cambio de la función con respecto a la
variable x, manteniendo constantes las otras variables y, z. De manera más precisa:
∂f (x, y, z)
f (x + ∆x, y, z) − f (x, y, z)
= lı́m
.
∆x→0
∂x
∆x
(1.49)
1.5. Ley de Gauss
44
1.5.6.1.
Ejemplo
Calcule las derivadas parciales de la función f (x, y, z) = x 2 yz 3 .
Solución
∂f
= 2xyz 3
∂x
∂f
= x 2z3
∂y
∂f
= 3x 2 yz 2
∂z
1.5.6.2.
Ejemplo
Sea ~r = xı̂ + y̂ + z k̂. Calcule la divergencia de ~r.
solución
∂
∂
∂
ı̂ + ̂ + k̂ · (xı̂ + y̂ + z k̂)
∂x
∂y
∂z
∂E
∂Ex
∂Ez
y
=
+
+
=1+1+1=3
∂x
∂y
∂z
~ · ~r =
∇
1.5.6.3.
Ejemplo
Consideremos una carga puntual q en el origen. El campo eléctrico que produce esta
carga en un punto ~r es
~ r ) = ke q r̂ = ke q ~r.
E(~
r2
r3
~ = ρ/ε0 . De modo que excepto en el
~ ·E
Mediante la ley de Gauss tenemos que ∇
origen, la densidad de carga es cero. Verifique este resultado.
~ = ∂ ı̂ + ∂ ̂ + ∂ k̂ · (Ex ı̂ + Ey ̂ + Ez k̂)
~ ·E
∇
∂x
∂y
∂z
∂Ey ∂Ez
∂Ex
=
+
+
∂x
∂y
∂z
de modo que
3
∂Ex
∂ x
r − 3xr 2 ∂r/∂x
= kq
= kq
= kq
∂x
∂x r 3
r6
!
1
3x
− ∂r
3
r
r 4 ∂x
1.5. Ley de Gauss
donde
45
∂r
2x
∂ 2
1
x
=
(x + y2 + z 2 )1/2 =
=
2
2
2
1/2
∂x
∂x
2 (x + y + z )
r
de manera que
∂Ex
= kq
∂x
3x 2
1
−
r3
r5
Se obtienen resultados correspondientes para las direcciones y, z, de modo que, para
r=
6 0 tenemos
~ = ∂Ex + ∂Ey + ∂Ez = kq
~ ·E
∇
∂x
∂y
∂z
1.5.7.
3
3(x 2 + y2 + z 2 )
−
r3
r5
=0
El Teorema de Gauss
Para un volumen ∆V suficientemente pequeño (infinitesimal), limitado por una
superficie ∆Σx , tenemos
I
1
~
~ · ν~ =
ν~ · dS
(1.50)
∇
∆V ∆Σ
I
~ = (∇
~ · ν~ )∆V .
⇒
ν~ · dS
(1.51)
∆Σ
Cualquier volumen V puede ser dividido en elementos de volumen ∆V a los cuales
podemos aplicar este resultado. Si sumamos las contribuciones de todos estos elementos
obtenemos, en el límite en que ∆V → 0,
Z
X
~ · ν~ dV .
~
∇
(1.52)
(∇ · ν~ )∆V →
V
R
~ sobre todos los elementos, cada
Por otro lado, al sumar los flujos de ∆Σ ν~ · dS
elemento de superficie de ∆Σ interno al volumen V es común a dos elementos de volumen
adyacentes, con sus normas orientadas en sentidos opuestos.
1.6. Potencial Eléctrico
46
Así, las contribuciones de los flujos de los elementos de superficies interiores se
cancelan de a pares, resultando sólo el flujo sobre la superficie externa S del volumen
V , o sea, la suma de los flujos resulta
I
XI
~
ν~ · dS = ν~ · d~s,
(1.53)
s
∆Σ
de modo que finalmente tendremos
Z
V
~ · ν~ dV =
∇
I
~
ν~ · dS.
s
(1.54)
~ y usando que ∇
~ = ρ/ε0
~ ·E
En particular, tomando para ν~ el campo electrostático E,
tenemos que
I
Z
Z
1
q
~
~
~
~
E · dS =
∇ · EdV =
ρdV = .
(1.55)
ε0 V
ε0
s
V
1.6.
Potencial Eléctrico
a energía potencial en un punto cualquiera bajo la presencia de un campo eléctrico es
una cantidad escalar. El concepto de potencial eléctrico tiene un gran valor práctico
en la operación de circuitos eléctricos y aparatos que estudiaremos.
L
~
E.
La carga de prueba q0 se mueve desde A hasta B en la región de un campo eléctrico
Figura 1.34: Trabajo de campo eléctrico.
Cuando la carga se coloca en algún punto del espacio donde existe un campo eléctrico,
el trabajo realizado sobre la carga es igual al trabajo realizado por el agente externo
para provocar el desplazamiento, pero con signo contrario.
1.6. Potencial Eléctrico
47
Para un desplazamiento infinitesimal d~l de una carga, el trabajo realizado por un
campo eléctrico sobre la misma es
~ · d~l.
F~ · d~l = q0 E
(1.56)
Conforme el campo realiza esta cantidad de trabajo, la energía potencial del sistema
cambia como
~ · d~l.
dU = −q0 E
(1.57)
Para un desplazamiento finito de la carga desde A hasta B tenemos
Z B
~ · d~l.
∆U = UB − UA = −WAB = −q0
E
A
(1.58)
La integración se lleva a cabo a lo largo de la trayectoria que q0 sigue al pasar de A
hasta B. Debido a que la fuerza eléctrica es conservativa, la integral de línea no depende
de la trayectoria tomada desde A hasta B.
1.6.1.
Integral curvilínea del campo eléctrico
~ es el campo eléctrico de cierta distribución estacionaria de cargas
Supongamos que E
~ entre dos puntos dados es:
eléctricas. La integral curvilínea de E
Z B
~ · d~l.
E
(1.59)
A
La integral de línea significa:
Dividir el camino en pequeños segmentos.
Representar cada segmento por un vector que une sus extremos.
~ en este
Efectuar el producto escalar del vector segmento de camino por el campo E
lugar.
Sumar estos productos para todo el camino.
La integral se considera el límite de la suma al hacer los segmentos cada vez más
pequeños y numerosos.
1.6. Potencial Eléctrico
48
1.6.1.1.
Ejemplo
~ donde E
~ = kyı̂ + kx̂ con k una constante. Si
Supongamos un campo eléctrico E
queremos realizar la integral curvilínea desde el punto A(0,0) hasta el punto B(2,2),
demuestre que es independiente del camino. Como ayuda, defina puntos intermediarios
C1 (1,2) y C2 (2,0), y demuestre que el resultado de la integral es independiente del punto
intermediario por donde pase.
solución
El vector que representa un elemento de camino es ds = dxı̂ + dy̂ y como el campo
~ = k(yı̂ + x̂) entonces, el producto escalar E
~ · d~s para un elemento de
eléctrico es E
~ s = k(yı̂ + x̂) · (dxı̂ + dy̂) = kydx + kxdy.
camino es Ed~
Vamos a calcular el segmento de camino desde A(0,0) hasta C1 (1,2):
Sea y(x) = mx + n
Por lo tanto,
Z
C1
A
y(0) = n = 0
⇒
y(x) = mx
y(1) = m = 2
⇒
y(x) = 2x
~ · d~s = k
E
C1
Z
A
⇒
Z
1
(ydx + xdy) = 4k
dy = 2dx
xdx = 2k
0
Para calcular el segmento de camino de C1 (1,2) hasta B(2,2) tenemos que y(x) = 2 ⇒
dy = 0, de manera que
Z B
Z B
Z 1
~
E · d~s = k
(ydx + xdy) = 2k
dx = 2k
C1
C1
0
Finalmente, la integral curvilínea a lo largo del camino AC1 B es
Z B
Z C1
Z B
~
~
~ · d~s = 2k + 2k = 4k
E · d~s =
E · d~s +
E
A
A
C1
Vamos ahora a calcular el segmento de camino desde A(0, 0) hasta C2 (2, 0), entonces
tenemos que y(x) = 0 ⇒ dy = 0, de modo que
Z C2
Z C2
~
E · d~s = k
(ydx + xdy) = 0
A
A
1.6. Potencial Eléctrico
2
49
Para calcular el segmento de camino de C2 (2, 0) hasta B(2, 2) tenemos que x(y) =
⇒ dx = 0, de manera que
Z
B
C2
~ · d~s = k
E
Z
B
C2
Z
(ydx + xdy) = 2k
2
= 4k
0
Finalmente, la integral curvilínea a lo largo del camino AC2 B es
Z
A
B
~ · d~s =
E
Z
C2
~ · d~s +
E
A
Z
De este modo concluimos que
A
B
Z
B1
C2
~ · d~s = 0 + 4k = 4k
E
~ · d~l tiene el mismo valor para todos los caminos
E
que unen A y B, en un campo eléctrico.
1.6.2.
Diferencia de potencial
Debido a que la integral curvilínea en el campo electrostático es independiente del
camino, podemos usarla para definir la siguiente magnitud escalar:
Z
∆U
=−
∆V = VB − VA =
q0
A
B
~ · d~l
E
J
v(volts) =
,
C
(1.60)
entonces ∆V es el trabajo por unidad de carga efectuado al mover una carga positiva
~ A esta cantidad se le conoce como
desde A a B en presencia de un campo eléctrico E.
diferencia de potencial entre los dos puntos.
1.6. Potencial Eléctrico
50
1.6.3.
Diferencia de potencial en un campo eléctrico uniforme
Figura 1.35: Diferencia de potencial entre dos puntos A y B en un
campo eléctrico uniforme.
Calculamos la diferencia de potencial entre dos puntos A y B separados por una
distancia |~l| = d, donde ~l es paralela a las líneas de campo
Z
∆V = VB − VA = −
A
B
~ · d~l = −
E
Z
A
B
Z
(E cos 0)dl = −E
A
B
dl = −Ed.
(1.61)
Las líneas de campo eléctrico siempre apuntan en dirección de la disminución del
potencial eléctrico (VA > VB ). El cambio de energía potencial correspondiente es
∆v =
∆U
q
⇒ ∆U = q∆V = −qEd.
(1.62)
(1.63)
Un sistema formado por una carga positiva y un campo eléctrico pierde energía
potencial eléctrica cuando la carga se mueve en la dirección del campo.
Si una carga de prueba en reposo es liberada en este campo eléctrico, ésta
~ Por lo tanto, la carga se acelerará hacia
experimentaría una fuerza eléctrica F~ = q0 E.
abajo, adquiriendo energía cinética. Conforme esta partícula cargada adquiere energía
cinética, el sistema pierde la misma cantidad de energía potencial.
1.6. Potencial Eléctrico
1.6.4.
51
Superficies equipotenciales
Imaginemos una partícula cargada que se mueve entre A y B en un campo eléctrico
uniforme, donde el vector ~l no es paralelo a las líneas de campo eléctrico.
Figura 1.36: Campo uniformemente dirigido, donde B está a un
potencial más bajo que el punto A. Los puntos B y C están al mismo
potencial.
De esta forma tendremos que
Z
∆V = −
A
B
~ · d~l = −E
~·
E
Z
A
B
~ · ~l = −El cos θ = −Ed.
dl = −E
(1.64)
Todos los puntos en un plano perpendicular a un campo eléctrico uniforme tienen el
mismo potencial eléctrico, de modo que, VB = VC .
Se define así la superficie equipotencial como cualquier superficie formada por una
distribución continua de puntos con el mismo potencial eléctrico.
1.6.4.1.
Ejemplo
Una batería produce una diferencia de potencial especifica ∆V entre dos conductores
conectados a las terminales de la batería. Una batería de 12 V está conectada entre
las dos placas paralelas. La separación entre ellas es de d = 0, 3 (cm). Determine la
magnitud del campo eléctrico entre las placas.
1.6. Potencial Eléctrico
52
solución
B
Z
∆V = −
A
~ · d~s = −
E
Z
d
~ · d~s = −E
E
0
Z
d
ds = −Ed
0
|∆V |
d
12
V
E=
−2
m
0, 3 · 10
V
E = 4 · 103
m
E=
1.6.4.2.
Ejemplo
Un protón se libera del reposo en un campo eléctrico uniforme 8 · 104 (V /m). El protón
~
sufre un desplazamiento de 0, 5 (m) en la dirección de E.
(a) Encuentre el cambio en el potencial eléctrico entre los puntos A y B.
solución
Z d
Z d
~
~
∆V = −
E · d~s = −
E · d~s = −E
ds = −Ed
A
0
0
V
∆V = −8 · 104
(0, 5(
m))
m
Z
B
∆V = −4 · 104 (V )
(b) Determine el cambio en la energía potencial del sistema para este desplazamiento.
solución
∆V =
⇒
∆U
q
∆U = q∆V = e∆V = (1, 6 · 10−19 (C ))(−4 · 104 (V )) = −6, 4 · 10−15 (J)
(c) Determine la velocidad del protón después de completar el desplazamiento de 0, 5(m)
en el campo eléctrico.
1.6. Potencial Eléctrico
53
solución
kA + UA = kB + UB
⇒ kA − kB = UB − UA = ∆U
⇒ kA − kB = −6, 4 · 10−15 (J)
como
1.6.5.
kA = 0
⇒ kB =
1 2
mν = 6, 4 · 10−15 (J)
2
s
2x6, 4 · 10−15 (J)
6 m
ν=
≈
2,
8
·
10
s
6, 67 · 10−27 (K g)
Gradiente de una función escalar
Dado el campo eléctrico, podemos calcular el potencial eléctrico
Z
∆V = −
B
~ · d~l,
E
A
(1.65)
Sin embargo, también podemos proceder en sentido contrario, es decir, conociendo el
potencial eléctrico podemos deducir el campo eléctrico. Para esto introduciremos el
concepto de vector gradiente de f como
~ (x, y, z) = ∂f (x, y, z) ı̂ + ∂f (x, y, z) ̂ + ∂f (x, y, z) k̂,
∇f
∂x
∂y
∂z
(1.66)
~ es un vector que expresa
donde f (x, y, z) es cierta función continua y derivable, y ∇f
como varía la función f (x, y, z) en la proximidad de un punto.
El gradiente de la función es un vector en la dirección de la máxima pendiente y
sentido ascendente, y su módulo es la pendiente, medida en aquella dirección.
1.6.6.
Deducción del campo eléctrico a partir del potencial
Consideremos el valor de V en dos puntos próximos (x, y, z) y (x + dx, y + dy, z + dz).
La variación del potencial V al pasar del primer punto al segundo es:
dV =
∂V
∂V
∂V
dx +
dy +
dz.
∂x
∂y
∂z
(1.67)
1.6. Potencial Eléctrico
54
Por otra parte,
Z
V =−
~ · d~l,
E
(1.68)
de modo que la variación puede también expresarse como
~ · d~l = ∂V dx + ∂V dy + ∂V dz
dV = −E
∂x
∂y
∂z
∂V
∂V
∂V
~ · d~l =
ı̂ +
̂ +
k̂ · (dxı̂ + dy̂ + dz k̂)
−E
∂x
∂y
∂z
~ · d~l = ∇V
~ · d~l,
−E
(1.69)
(1.70)
(1.71)
de manera que el campo eléctrico es el gradiente, cambiado de signo, del potencial
~ = −∇V
~ .
E
1.6.6.1.
Ejemplo
Si V = 3x 2 y + y2 + yz encuentre el campo eléctrico.
Solución
~ = −∇V
~ =−
E
1.6.7.
∂V
∂V
∂V
ı̂ +
̂ +
k̂
∂x
∂y
∂z
= −6xyı̂ − (3x 2 + 2y + z)̂ − yk̂
Potencial eléctrico de cargas puntuales
Figura 1.37: Diferencia de potencial entre los puntos A y B debido a
la carga puntual q.
(1.72)
1.6. Potencial Eléctrico
55
El potencial eléctrico en un punto ubicado a una distancia r de una carga q, está
dado por
Z B
~ · d~l,
E
(1.73)
∆V = VB − VA = −
A
pero el campo eléctrico es
de modo que
~ = ke q r̂,
E
r2
(1.74)
~ · d~l = ke q r̂d~l = ke q dl cos θ.
E
r2
r2
(1.75)
Usando dr = dl cos θ, entonces
~ · d~l = ke q dr,
E
r2
de modo que
B
Z
∆V = VB − VA = −ke q
A
dr
= ke q
r2
(1.76)
1
1
−
rB
rA
.
(1.77)
En general se elige la referencia del potencial eléctrico de una carga puntual, de
forma que sea VA = 0 ⇒ rA = ∞. Así, el potencial debido a una carga puntual es
q
V = ke .
r
(1.78)
Ahora, el potencial eléctrico resultante de dos o más cargas puntuales se obtiene
mediante la aplicación del principio de superposición
V = ke
X qi
i
1.6.7.1.
ri
.
(1.79)
Ejemplo
Una carga puntual q1 = 1(µC ) está en el origen y una segunda carga q2 = −4 (µC )
localizada en (4, 0)(m). Encuentre el potencial eléctrico total en el punto P(0, 3)(m).
Solución
Consideremos ahora la energía potencial de un sistema formado por dos partículas
cargadas. Si V2 es el potencial eléctrico en un punto P debido a la carga q2 , entonces el
1.6. Potencial Eléctrico
56
trabajo de trae una segunda carga q1 desde el infinito hasta P sin aceleración es q1 V2 .
Así, la energía potencial del sistema es:
U = q1 V2 = ke
q1 q2
r12
Si el sistema consiste de más de dos partículas cargadas, la energía potencial total
está dada por
q1 q2 q1 q3 q2 q3
U = ke = ke
+
+
r12
r13
r23
1.6.7.2.
Ejercicio
Una carga q1 = 2(µC ) se localiza en el origen, y una carga q2 = −61(µC ) está en
(0, 3)(m).
(a) Determine el potencial eléctrico total debido a estas cargas en el punto P(4, 0)(m).
(b) Determinar el cambio en energía potencial del sistema de dos cargas, además de una
carga q3 = 3 (µC ), conforme la última carga se mueve desde el infinito hasta el punto
P.
(c) Determinar el cambio en la energía potencial cuando las tres cargas parten
infinitamente separadas unas de las otras.
1.6.7.3.
Ejercicio
Un dipolo eléctrico consiste de dos cargas de magnitud equivalente y de signo
contrario, separadas por una distancia 2a. El dipolo se encuentra a lo largo del eje
de las x y su centro está en el origen.
1.6. Potencial Eléctrico
57
Figura 1.38: Dipolo eléctrico, separado por una distancia 2a
(a) Calcule el potencial eléctrico en el punto P.
(b) Calcule V y Ex en un punto alejado del dipolo. Utilice x a.
(c) Calcule V y Ex si el punto P está localizado en cualquier sitio entre las dos cargas.
1.6.8.
Potencial eléctrico para distribuciones continuas de carga
Existen dos métodos para calcular el potencial eléctrico debido a una distribución
continua de carga
(a) Subdividimos la distribución de carga en pequeños elementos de carga dq y usamos
el resultado de carga puntual
Z
dq
V = ke
(1.80)
r
(b) Si conocemos el campo eléctrico, por ejemplo mediante la ley de Gauss, entonces
podemos usar la siguiente expresión
Z
∆V = −
A
B
~ · d~l
E
(1.81)
Este cálculo entregará el potencial entre los puntos A y B, de manera que
necesitaremos definir V = 0 en algún punto conveniente.
1.6. Potencial Eléctrico
58
1.6.8.1.
Ejercicio
Una varilla de longitud l localizada a lo largo del eje de las x tiene una carga total
Q y una densidad de carga lineal λ = Q/l. Determine el potencial eléctrico en un punto
P localizado en el eje de las y, a una distancia a del origen.
Figura 1.39: Barilla de carga uniforme Q colocada a los largo del eje
x.
1.6.8.2.
Ejercicio
Estudiemos el potencial eléctrico debido a un anillo uniformemente cargado.
(a) Encuentre una expresión para el potencial eléctrico en un punto localizado en la
perpendicular al eje central de un anillo uniformemente cargado, de radio a y carga
Q.
(b) Encuentre una expresión para la magnitud del campo eléctrico en el punto P.
1.6.8.3.
ejercicio
Un disco uniformemente cargado tiene un radio R y una densidad de carga superficial
σ.
(a) Determine el potencial eléctrico a lo largo del eje central perpendicular al disco.
(b) Determine la magnitud del campo eléctrico a lo largo del eje central perpendicular
al disco.
1.6. Potencial Eléctrico
1.6.8.4.
59
ejercicio
Una esfera aislada de radio R tiene una densidad de carga volumétrica positiva
uniforme y carga total Q.
(a) Determine el potencial eléctrico en un punto fuera de la esfera, esto es, para r > R.
Haga que el potencial en r = ∞ sea igual a cero.
(b) Determine el potencial eléctrico en un punto en el interior de la esfera, esto es, para
r < R.
1.6.9.
Laplaciana
Acabamos de encontrar dos funciones escalares relacionadas con el campo eléctrico,
~ En coordenadas cartesianas, las relaciones se
~ · E.
el potencial V y la divergencia ∇
expresan como:
∂V
∂V
∂V
~
~
ı̂ +
̂ +
k̂
(1.82)
E = −∇V = −
∂x
∂y
∂z
~ = ∂ ı̂ + ∂ ̂ + ∂ k̂ · (Ex ı̂ + Ex ̂ + Ex k̂)
~ ·E
∇
(1.83)
∂x
∂y
∂z
~ = ∂Ex + ∂Ey + ∂Ez ,
~ ·E
∇
(1.84)
∂x
∂y
∂z
~ yV
~ ·E
De modo que podemos encontrar una relación entre ∇
∂
∂
∂V
∂V
∂V
∂
~
~
~
~
∇ · E = ∇ · (−∇V ) = −
ı̂ +
̂ + k̂ ·
ı̂ +
̂ +
k̂
∂x
∂y
∂z
∂x
∂y
∂z
2
∂ V
∂2 V
∂2 V
2
~
~
∇ · E = −∇ V = −
+
+
.
∂x 2
∂y2
∂z 2
(1.85)
(1.86)
La notación ∇2 se explica como sigue. El operador gradiente se simboliza
~ llamado nabla. En coordenadas cartesianas
frecuentemente por ∇,
∂
∂
∂
~ =
∇
ı̂ +
̂ + k̂ ,
(1.87)
∂x
∂y
∂z
si lo tratamos como un vector, su cuadrado (modulo) sería entonces el laplaciano
2
∂
∂2
∂2
2
~
~
∇ =∇·∇=
+
+
.
(1.88)
∂x 2 ∂y2 ∂z 2
1.6. Potencial Eléctrico
60
Podemos obtener así una relación local entre la densidad de carga en un punto y el
potencial en su vecindad inmediata. De la ley de Gauss en su forma diferencial tenemos
~= ρ,
~ ·E
∇
ε0
(1.89)
de modo que
⇒
~ =∇
~ ·E
~ · (−∇V
~ ) = −∇2 V = ρ
∇
ε0
−ρ
∇2 V =
Ecuación de poisson.
ε0
(1.90)
(1.91)
La ecuación de Poisson relaciona la densidad de cargas con las segundas derivadas
del potencial.
1.6.10.
Ecuación de Laplace
Dondequiera que ρ = 0, es decir, en todas las regiones del espacio que no contengan
cargas eléctricas, el potencial eléctrico tiene que satisfacer la ecuación
∇2 V = 0 Ecuación de Laplace.
(1.92)
El tipo de funciones que satisfacen la ecuación de Laplace se llaman funciones
armónicas.
1.6.11.
Rotacional de una función vectorial
Consideremos la integral de línea de cierto campo vectorial F~ (x, y, z) tomada a lo
largo de un camino cerrado, una curva C la cual se cierra sobre sí misma.
1.6. Potencial Eléctrico
61
Figura 1.40: integral de línea de un cierto campo vectorial F~ sobre un
camino cerrado C el cual es el contorno de una superficie S.
La integral curvilínea a lo largo de una línea cerrada es la circulación
I
Γ = F~ · d~l.
c
(1.93)
Ahora dividimos C con un nuevo camino B, formando de este modo dos bucles, C1 y
C2 , cada uno de los cuales incluye B como parte del mismo camino.
Figura 1.41: División del el camino cerrado C en dos.
La suma de las circulaciones Γ1 y Γ2 , sera la misma que la circulación original a
lo largo de C, ya que, el puente está atravesado en sentidos contrarios en las dos
integraciones, dejando solamente las contribuciones que constituyen la integral curvilínea
original a lo largo de C.
1.6. Potencial Eléctrico
62
Nuevas subdivisiones en varios bucles C1 , C2 , . . ., CN dejan la suma invariable
Z
Γ=
C
F~ · d~l =
N
X
Γi =
i=1
N I
X
i=1
F~ · d~li .
Ci
(1.94)
Cuando subdividimos los bucles, hacemos bucles de menor circulación, pero también
de menor área. Así, es natural considerar la relación de circulación del bucle al área de
éste. Definimos entonces el vector rotacional de F~ (x, y, z) como
I
F~ · d~l
Γ
i
C
i
~ · F~ ) · n̂ = lı́m
(∇
= lı́m
,
(1.95)
ai →0 ai
ai →0
ai
donde el vector unitario n̂ denota la normal a la superficie considerada, y este vector debe
permanecer constante cuando la superficie que rodea un punto particular P disminuye
tendiendo a cero.
En la siguiente figura mostramos la Regla del Tornillo o de la mano derecha que
relaciona la normal a la superficie con el sentido que se toma en la integral curvilínea
de la circulación.
Figura 1.42: Asociamos a cada superficie ai su vector normal n̂i
mediante la regla de la mano derecha para su sentido.
1.6.12.
Teorema de Stokes
De la circulación alrededor de una porción de superficie infinitesimal podemos volver
a la circulación a lo largo del bucle original C
I
Γ=
C
F~ · d~l =
N
X
i=1
Γi =
N
X
i=1
ai
Γi
ai
N
X
=
i=1
~ F~ ) · n̂i ,
ai (∇x
(1.96)
1.6. Potencial Eléctrico
63
de modo que
I
C
1.6.13.
F~ · d~l =
Z
s
~
~ F~ ) · dS.
(∇x
(1.97)
El rotacional en coordenadas cartesianas
Vamos a considerar un bucle en el plano xy con n̂ = k̂.
Figura 1.43: Bucle en el plano xy.
De esta forma tendremos que
∆x ∂Fx
+ ...
2 ∂x
∂Fy ∆y ∂Fy
Fy (2) = Fy (x, y) + ∆x
+
+ ...
∂x
2 ∂y
∆x ∂Fx
∂Fx
Fx (3) = Fx (x, y) +
+ ∆y
+ ...
2 ∂x
∂y
∆y ∂Fy
Fy (4) = Fy (x, y) +
+ ...,
2 ∂y
Fx (1) = Fx (x, y) +
(1.98)
(1.99)
(1.100)
(1.101)
así pues, despreciando los términos de orden superior de ∆x y de ∆y, la integral a lo
largo de todo el rectángulo es
I
∂Fy ∆y ∂Fy
∆x ∂Fx
~
~
F · dl = ∆x Fx (x, y) +
+ ∆y Fy (x, y) + ∆x
+
2 ∂x
∂x
2 ∂y
C
∆x ∂Fx
∂Fx
∆y ∂Fy
− ∆x Fx (x, y) +
+ ∆y
− ∆y Fy (x, y) +
, (1.102)
2 ∂x
∂y
2 ∂y
de manera que simplificando
I
C
F~ · d~l = ∆x∆y
∂Fy ∂Fx
−
∂x
∂y
,
(1.103)
1.6. Potencial Eléctrico
64
ahora bien, ∆x∆y es el valor del área del rectángulo contenido el cual hemos representado
por un vector en la dirección z. Evidentemente,
∂Fy ∂Fx
Integral alrededor del rectángulo
=
−
.
∂x
∂y
Área del rectángulo
(1.104)
Si la figura rectangular se ha orientado con su normal en el sentido positivo de y,
tendríamos
∂Fy ∂Fx
−
,
(1.105)
∂x
∂y
y si el cuadro se orienta con su normal en la dirección x, entonces
∂Fy
∂Fz
−
,
∂y
∂z
de esta forma obtendremos como fórmula general
∂F
∂F
∂F
∂F
∂F
∂F
y
y
z
x
z
x
~ × F~ =
∇
k̂.
−
ı̂ +
−
̂ +
−
∂y
∂z
∂z
∂x
∂x
∂y
(1.106)
(1.107)
Existe una manera más fácil para recordar la regla anterior, y es que el resultado del
rotacional se puede escribir como el determinante siguiente
ı̂
̂
k̂
∂
∂ ~ × F~ = ∂
∇
(1.108)
∂x ∂y ∂z Fx Fy Fz 1.6.14.
Significado físico del rotacional
El nombre rotacional nos recuerda que un campo vectorial con rotacional distinto de
cero tiene circulación o turbulencia. Por ejemplo, el campo de velocidades del agua al
vaciar una bañera adquiere, generalmente, una circulación. Su rotacional no es cero en
la mayor parte de la superficie. Cualquier cosa que flote en la superficie del agua girará
mientras avanza.
En el caso del campo electrostático concluimos que
~ = 0 (en todo el espacio),
~ E
∇x
(1.109)
~ a lo largo de todo el
ya que en el campo electrostático, la integral curvilínea de E
~ entre dos puntos
camino cerrado es nula. Esto debido a que la integral curvilínea de E
es independiente de la trayectoria.
1.7. Campo eléctrico en conductores
65
1.7.
Campo eléctrico en conductores
1.7.1.
Clasificación de los materiales
Los conductores eléctricos son aquellos materiales en los cuales algunos de los
electrones son libres, es decir, no están unidos a átomos y pueden moverse con relativa
libertad a través del material. Un átomo de metal tiene uno o más electrones exteriores,
unidos en forma débil al núcleo. Cuando se combinan muchos átomos para formar un metal,
los electrones exteriores, que no están unidos a ningún átomo, se mueven por el metal de
una forma similar a como lo hacen las moléculas de gas en el interior de un recipiente.
Cuando los metales son cargados en alguna región pequeña, la carga se distribuye de
inmediato sobre toda la superficie de éste. Algunos de los máximos exponentes son el
oro, cobre, plata y aluminio.
Los aislantes eléctricos son aquellos materiales en los cuales todos los electrones
están unidos a átomos y no pueden moverse libremente a través del material. Cuando se
frotan estos materiales, sólo la zona frotada se carga, y las partículas cargadas no pueden
moverse hacia otras zonas del material. Algunos exponentes son el vidrio, el caucho y la
madera.
Una tercera clase de materiales son los semiconductores, cuyas propiedades eléctricas
se ubican en algún sitio entre las correspondientes a los aislantes y a los conductores.
Las propiedades eléctricas de los semiconductores pueden cambiar, a varios órdenes
de magnitud, mediante la adición de cantidades controladas de ciertos átomos a dichos
materiales. Algunos exponentes son el silicio y el germanio, los cuales se utilizan en chips
electrónicos.
Material
Electrones libres/cm3
Conductores
1022
Semiconductores
1012
Aislantes
102
Cuadro 1.2: Clasificación de materiales
1.7. Campo eléctrico en conductores
66
1.7.2.
Conductores en equilibrio electrostático
Un buen conductor contiene cargas (electrones) que no están ligadas a ningún átomo,
y así, son libres de moverse dentro del material. Cuando no hay movimiento de carga
neta dentro de un conductor, se dice que el conductor está en equilibrio electrostático, y
entonces presenta las siguientes propiedades:
(a) El campo eléctrico es cero dentro de un conductor
El campo eléctrico dentro de un conductor debe ser cero bajo la superposición de que
estamos en equilibrio electrostático. Si el campo no es cero, las cargas libres en el
conductor deberían acelerar bajo la acción del campo. El movimiento de electrones,
sin embargo, significaría que el conductor no estuviese en equilibrio electrostático.
En el caso de una lámina conductora en presencia de un campo externo, las cargas
inducidas sobre las dos superficies producen un campo eléctrico que se opone al
campo eléctrico externo, dando un campo neto cero dentro de las placas.
Antes de que apliquemos un campo externo, los electrones libres están uniformemente
distribuidos dentro del conductor. Cuando aplicamos un campo externo, los electrones
libres aceleran hacia la izquierda, causando un plano de cargas negativas en esta
superficie.
Figura 1.44: Lámina conductora en un campo eléctrico externo Eext .
El movimiento de electrones hacia la izquierda produce un plano de cargas positivas
en la superficie de la derecha. Estos planos de carga crean un campo eléctrico
1.7. Campo eléctrico en conductores
67
adicional dentro del conductor que se opone al campo externo. Los electrones se
mueven hasta que los campos se igualan, y el campo neto dentro del conductor es
cero.
Un buen conductor alcanza el equilibrio electrostático típicamente en un tiempo de
10−16 (s).
(b) Si un conductor aislado lleva cargas, éstas residen en su superficie
Figura 1.45: Superficie gaussiana en el interior de un conductor de
forma arbitraria.
Recordemos que el campo eléctrico dentro del conductor es cero cuando éste está
en equilibrio electrostático. Entonces, el campo eléctrico debe ser cero en cualquier
punto sobre la superficie gaussiana
I
φ=
~ · dS
~ =E
~S
~ = qint .
E
ε0
s
Debido a que no hay carga neta dentro de la superficie gaussiana, entonces la carga
neta sobre el conductor debe residir sobre su superficie.
(c) El campo eléctrico en el borde exterior de un conductor cargado es perpendicular a
la superficie del conductor y tiene una magnitud σ /ε0
1.7. Campo eléctrico en conductores
68
Figura 1.46: Flujo a través de una superficie gaussiana en forma
cilíndrica, para un conductor cargado.
El campo eléctrico es normal a la superficie del conductor debido a la condición
~ tiene una componente paralela a la superficie del
de equilibrio electrostático. Si E
conductor, las cargas libres deberían moverse a lo largo de la superficie. En tal caso,
el conductor no estará en equilibrio
I
~ · dS
~ = ES = qint = σ S
φ=
E
ε0
ε0
S
σ
E= .
ε0
Como el campo eléctrico en el interior del conductor es cero, sólo contribuye la
superficie externa.
(d) En un conductor de forma irregular, la densidad de carga superficial es mayor en
aquellas posiciones donde el radio de curvatura de la superficie es menor.
Debido a que el campo eléctrico justo fuera del conductor es proporcional a la
densidad de carga superficial, vemos que el campo eléctrico es grande cerca de
puntos que tienen pequeños radios de curvatura.
1.7.3.
Potencial eléctrico debido a un conductor cargado
Ya demostramos que el campo eléctrico dentro de un conductor es cero. Además,
cualquier carga neta que exista reside sobre la superficie del conductor, y que el campo
1.7. Campo eléctrico en conductores
69
eléctrico inmediatamente fuera del conductor es perpendicular a su superficie.
Figura 1.47: Conductor de forma arbitraria con un exceso de cargas
positivas.
Consideremos los puntos A y B sobre la superficie del conductor cargado. A lo largo
~ es siempre perpendicular a d~l
de un camino superficial que conecta estos puntos, E
Z
∆V = VB − VA = −
A
B
~ · d~l = 0
E
(1.110)
~ · d~l = 0
E
(1.111)
VB = VA .
(1.112)
Por lo tanto, V es constante en cualquier punto de la superficie de un conductor
cargado en equilibrio. Además, debido a que el campo eléctrico es igual a cero en el
interior del conductor, entonces el potencial eléctrico es constante en cualquier punto en
el interior y en la superficie del conductor.
1.7.3.1.
Ejemplo
Una esfera sólida metálica de radio a con una carga Q está en el centro de un
cascarón esférico metálico de radio interno b y radio externo c con una carga neta igual
a cero. Encuentre el potencial eléctrico en:
1.7. Campo eléctrico en conductores
70
(a) r > c
I
s
~ · d~s =E(4πr 2 )
E
⇒ E(4πr 2 ) =
~ = k Q r̂
⇒ E
r2
Z
VB − VA = −
r
∞
~ · d~l = −kQ
E
Z
r
∞
Q
ε0
dr
= kQ
r2
1
1
−
r
∞
pero VA = 0 : r → ∞
VB = k
Q
r
(b) b ≤ r ≤ c
Como el potencial tiene que ser continuo en r = c entonces
Q
r=c
c
I
~ · d~s = qint ⇒ E = 0 b ≤ r ≤ c por ser conductor
E
ε0
S
Z r
~ · d~l = 0
entonces VD − VC = −
E
Vc = k
c
Q
⇒ VD = VC = k
b<r<c
c
Como el potencial tiene que ser continuo en r = b entonces
VE = k
Q
c
r=b
(c) a ≤ r ≤ c
I
s
~ · d~s =E(4πr 2 )
E
⇒ E(4πr 2 ) =
~ = k Q r̂
⇒ E
r2
a<r<b
Z r
dr
1 1
~
~
VF − VE = −
E · dl = −kQ
= kQ
−
2
r
b
b
b r
1 1
1 1 1
entonces VF = kQ
−
+ VE = kQ
− +
a<r<b
r
b
r
b c
Z
r
Q
ε0
1.7. Campo eléctrico en conductores
71
(d) r < a
Como el potencial tiene que ser continuo en r = a entonces
1 1 1
r=a
VG = kQ
− +
r
b c
I
~ · d~s = qint ⇒ E = 0 r < a por ser conductor
E
ε0
S
Z r
~ · d~l = 0
VH − VG = −
E
a
1 1 1
r<a
− +
VH = VG = kQ
r
b c
1.7.4.
Método de las imágenes
El sistema, aproximadamente más simple, en el cual se pone en evidencia la movilidad
de las cargas en el conductor es una carga puntual próxima a un conductor plano.
Supongamos que el plano xy es la superficie de un conductor indefinido. Asignemos
a este plano el potencial cero.
Tomamos ahora una carga positiva Q y la colocamos en el eje z a una distancia z del
plano xy. ¿Qué tipo de campo eléctrico y qué distribución de carga podemos esperar?
Figura 1.48: Sistema equidistantes para una carga y su carga imagen.
Para resolver el problema vamos a usar un artificio que es a la vez útil e instructivo.
En este caso vamos a considerar el problema de dos cargas puntuales de signo contrario
1.7. Campo eléctrico en conductores
72
Q y −Q
ke Qy
ke Qz
̂ − 2
k̂
(z 2 + y2 )3/2
(z + y2 )3/2
ke Qy
ke Qz
~2p =
k̂
E
̂ − 2
2
2
3/2
(z + y )
(z + y2 )3/2
~ =E
~1p + E
~2p = − 2ke Qz .
entonces E
(z 2 + y2 )3/2
~1p = −
E
Ahora, usando la ley de Gauss tenemos
I
~ · dS
~ = qint
E
ε0
s
σS
ES =
ε0
⇒ σ = ε0 E,
(1.113)
(1.114)
(1.115)
(1.116)
(1.117)
(1.118)
esto nos indica que la densidad superficial de carga σ es
σ =−
1.7.5.
Qz
.
+ y2 )3/2
2π(z 2
(1.119)
Elementos en circuitos eléctricos
Los elementos simples de los circuitos que se pueden interconectar mediante alambres
para forma un circuito eléctrico son:
Capacitores: dispositivos que almacenan carga eléctrica.
Resistores
Inductores
Algunos elementos más complejos son:
Diodos
Transistores
Los capacitores (o condensadores) se usan:
1.7. Campo eléctrico en conductores
73
para sintonizar la frecuencia de las radios.
en filtros de fuentes de energía eléctrica (automóviles).
para almacenar energía en los flash electrónicos.
1.7.6.
Definición de la capacitancia
Dos placas conductoras planas se colocan paralelamente separadas una distancia d.
Figura 1.49: Sistema de dos placas planas conductoras cargadas
separadas por una distancia d
Sea A el área de cada placa y supongamos que una placa contiene la carga Q y la
otra −Q. Los valores del potencial en cada una de las placas son V1 y V2 . Excepto en los
bordes, el campo eléctrico es casi uniforme en la región entre las placas. Considerando
que el campo es uniforme tenemos
Z
∆V =V2 − V1 = −
despejando, tenemos E =
~ · d~l = −Ed
E
|V2 − V1 |
.
d
(1.120)
(1.121)
Recordemos que el campo eléctrico de una placa paralela es
I
2
~ · dS
~= Q
E
ε0
s
Q
2EA =
ε0
Q
⇒ E=
.
2ε0 A
(1.122)
(1.123)
(1.124)
1.7. Campo eléctrico en conductores
74
En el caso de un par de placas paralelas tenemos
pero entre las placas
~ =E
~1 + E
~2 = 2
E
Q
2ε0 A
,
(1.125)
de modo que la carga es
Q = ε0 AE =
ε0 A
(|V2 − V1 |).
d
(1.126)
Nuestro par de placas es un ejemplo de un elemento común en los sistemas
electrónicos, el condensador. Un condensador es simplemente dos conductores próximos,
a diferentes potenciales y que contienen cargas distintas. Nos interesa la relación entre
la carga Q de una de las placas y la diferencia de potencial entre ellas
C=
Q
ε0 A
=
|V2 − V1 |
d
[f (faraday)].
(1.127)
A esta constante, que sólo depende de la geometría, le llamamos capacidad del
condensador. La capacidad de un condensador de placas paralelas es proporcional a
la superficie de sus placas e inversamente proporcional a la separación de las mismas.
1.7. Campo eléctrico en conductores
1.7.6.1.
75
Ejemplo
Un conductor cilíndrico sólido de radio a y carga Q está colocado en forma coaxial
a un cascarón cilíndrico de espesor despreciable, de radio b > a, y con una carga −Q.
Determine la capacitancia de este capacitor cilíndrico si su longitud es igual a L.
Figura 1.50: Conductor cilíndrico de radio a, rodeado por un cascarón
cilíndrico coaxial de radio b.
Solución
Usando la Ley de Gauss calcularemos el campo eléctrico.
I
~ · d~s = E(2πrL) = qint = Q = λL
E
ε0
ε0
ε0
S
~ = λ r̂ = 2kλ r̂
E
2πε0 r
r
De este modo, la diferencia de potencial es
Z b
Z b
dr
b
~ · d~l = −2kλ
E
= −2kλ ln
∆V = Vb − Va = −
a
a
a r
Así, la capacitancia será
C=
λ L
Q
=
|∆V |
2k λ ln
c
a
=
L
2k ln
c
a
El cable coaxial es un ejemplo de este tipo de configuración geométrica, ya que está
formado por dos conductores cilíndricos concéntricos separados por un material aislante.
El cable transporta señales eléctricas tanto en el conductor interior como en el exterior.
Esta geometría es útil para proteger las señales de cualquier tipo de interferencias
externas.
1.8. Circuito eléctricos básicos
76
1.7.6.2.
Ejemplo
Un capacitor esférico está formado de un cascarón conductor esférico de radio b y de
carga −Q concéntrico con una esfera conductora más pequeña de radio a y de carga Q.
Determine la capacitancia de este dispositivo.
Solución
Usando la Ley de Gauss calcularemos el campo eléctrico.
I
~ · d~s = E(4πr 2 ) = qint = Q
E
ε0
ε0
S
~ = k Q r̂ = k Q ~r
⇒ E
r2
r2
De este modo, la diferencia de potencial es
Z b
Z b
dr
1
1
(b − a)
~
~
∆V = Bb − Va =
E · dl = −kQ
= kQ
−
= −kQ
2
b a
ab
a
a r
Así, la capacitancia será
C=
Q
Q
ab
=
=
(b−a)
|∆V |
k(b − a)
k
Q
ab
1.8.
Circuito eléctricos básicos
Para el estudio de los circuitos eléctricos utilizaremos una representación gráfica
simbólica que se conoce como diagrama del circuito.
Figura 1.51: Símbolos en circuitos para condensadores, baterías,
conductores e interruptores.
1.8. Circuito eléctricos básicos
1.8.1.
77
Capacitores en paralelo
Las placas izquierdas de los capacitores están unidas al mismo terminal de la batería.
Las placas derechas de ambos capacitores están conectadas al mismo terminal de la
batería.
Figura 1.52: Conexión en paralelo de dos condensadores, donde la
diferencia de potencial aplicada a ambos es la misma.
Las diferencias de potencial individuales en capacitores conectados en paralelo son
las mismas e iguales a la diferencia de potencial aplicado a través de la combinación.
Cuando se conectan los capacitores se transfieren electrones entre los alambres y las
placas. El flujo de la carga se termina o cesa cuando el voltaje aplicado a través de los
capacitores es igual al que está presente a través de las terminales de la batería. Cuando
el flujo cesa, los capacitores han alcanzado su carga máxima.
La carga total Q almacenada por ambos capacitores es
Q = Q1 + Q2 .
(1.128)
Queremos ahora reemplazar los dos capacitores con uno que es equivalente, Ceq
(
Q1 = C1 ∆V
Q
⇒
(1.129)
C=
∆V
Q2 = C2 ∆V
Q = Q1 + Q2 = C1 ∆V + = C2 ∆V
(1.130)
Q = (C1 + C2 )∆V
(1.131)
Q = Ceq ∆V
(1.132)
1.8. Circuito eléctricos básicos
78
La capacitancia equivalente de una combinación de capacitores en paralelo es la
suma algebraica de las capacitancias individuales,
Ceq = C1 + C2 + C3 + . . .
1.8.2.
Combinación en paralelo
(1.133)
Capacitores en serie
La placa izquierda de C1 y la placa derecha de C2 están conectadas a la batería.
Figura 1.53: Conexión en serie de dos condensadores, donde la
diferencia de potencial es la suma de las diferencias aplicada a los
condensadores individuales.
Al conectar la batería, se transfieren electrones que salen de la placa izquierda de
C1 y entran en la placa derecha de C2 . Conforme se acumula esta carga negativa en
la placa derecha de C2 , una cantidad equivalente de carga negativa es expulsada de la
placa izquierda de C2 resultando esta placa izquierda con un exceso de carga positiva.
La carga negativa que sale de la placa izquierda de C2 hace que se acumulen cargas
negativas en la placa derecha de C1 . Así, las cargas de los capacitores conectados en
serie son iguales. El voltaje ∆V a lo largo de las terminales de la bateria se divide entre
los capacitores, ∆V = ∆V1 + ∆V2 , de modo que
Q
Q
=
∆V
∆V1 + ∆V2
1
∆V1 + ∆V2
∆V1 ∆V2
=
=
+
Ceq
Q
Q
Q
1
1
1
=
+
Ceq
C1 C2
Ceq =
(1.134)
(1.135)
(1.136)
1.8. Circuito eléctricos básicos
79
Para más de dos capacitores tendremos
1
1
1
1
=
+
+
+ ...
Ceq
C1 C2 C3
Capacitores en serie
(1.137)
El inverso de la capacitancia equivalente es la suma de los inversos de las capacitancias
individuales.
1.8.2.1.
Ejemplo
Encuentre el valor de la capacitancia equivalente entre a y b de la combinación de
capacitores. Todas las capacitancias se entregan en valores de µF .
Figura 1.54: Red de condensadores
solución
Aplicando las propiedades de condensadores en serie y en paralelo obtendremos que
la capacitancia efectiva será Cef f = 25/12 (µF )
1.8.2.2.
Ejemplo
En el ejemplo anterior, conectamos una batería de 12 (V ) entre los puntos a y b.
Determine la carga sobre cada capacitor y la diferencia de potencial.
solución
Q = Cef f ∆V =
25
(µF ) (12(V )) = 12 (µC )
12
como Q ≡ Q2 = Q12 = Q1 = 25 (µC )
1.8. Circuito eléctricos básicos
80
ahora
Q
25 (µC )
25
=
=
(V )
C2
2 (µC )
2
25 (µC )
Q
=
= 1 (V )
∆V1 =
C1
1 (µC )
Q
25 (µC )
25
∆V12 =
=
=
(V )
C12
12 (µC )
12
∆V2 =
como
∆V12 ≡ ∆V5 = ∆V7 =
25
(V )
12
⇒ Q5 = C5 ∆V12
⇒ Q7 = C7 ∆V12
1.8.3.
25
125
= (5 (µC ))
(V ) =
(µF )
12
12
25
175
= (7 (µC ))
(V ) =
(µF )
12
12
Energía almacenada en un capacitor cargado
Si las placas de un capacitor se encuentran conectadas mediante un conductor
(alambre), la carga se moverá entre las placas y el alambre que las conecta hasta que
el capacitor se descargue. Un capacitor de placas paralelas descargado no presenta una
diferencia de potencial entre sus placas.
El capacitor está conectado a una batería que suministra una carga Q a las placas.
El capacitor se carga completamente cuando la diferencia de potencial entre las placas
1.8. Circuito eléctricos básicos
81
es ∆V = Q/C . De inicio, no se requiere de trabajo para transferir una pequeña cantidad
de carga dq de una placa a la otra. Sin embargo, una vez transferida esta carga, aparece
una pequeña diferencia de potencial y deberá entonces efectuarse trabajo para mover
carga adicional.
q
∆V =
c
(
Diferencia de potencial en un instante
cuando se ha transferido una carga q
(1.138)
El trabajo para mover una carga dq desde (−q) hasta (+q) es:
dW = ∆V dq =
q
dq
C
(1.139)
Figura 1.55: Trabajo necesario para cargar un condensador
El trabajo total requerido para cargar el capacitor es
Q
Z
w=
0
Z
1
dW =
C
Q
qdq =
0
Q2
,
2C
(1.140)
usando la relación C = Q/∆V , entonces podemos escribir la energía como
U=
Q2
1
1
= Q∆V = C (∆V )2 .
2C
2
2
(1.141)
Para el caso de un condensador de placas paralelas, la diferencia de potencial entre
las placas es
Z d
~ · d~l = −Ed,
∆V =
E
(1.142)
0
1.8. Circuito eléctricos básicos
82
donde el campo eléctrico es
I
~ · dS
~ = qint
E
ε0
S
σ
A
⇒ E
A=
ε0
σ
E= ,
ε0
y la capacitancia es
C=
Q
σA
ε0 A
=
=
,
|∆V |
Ed
d
(1.143)
(1.144)
(1.145)
(1.146)
de modo que la energía es
1
C (∆V )2
2
1
1 ε0 A
(Ed)2 = ε0 E 2 Ad,
=
2 d
2
U=
(1.147)
(1.148)
de forma que podemos definir la densidad de energía almacenada en un capacitor como
µE =
U
U
1
=
= ε0 E 2 .
V
Ad
2
(1.149)
La densidad de energía en cualquier campo eléctrico en un punto dado es proporcional
al cuadrado de la magnitud del campo eléctrico.
Ejercicios Propuestos
Electrostática.
1. Calcule la carga neta en una sustancia que está formada por:
(a) 5 × 1013 electrones.
(b) Una combinación de 4, 3 × 1014 protones y 2, 5 × 1014 electrones.
2. Si frota un globo inflado contra su cabello, ambos materiales se atraen. La carga
presente en el sistema formado por el globo y su cabello después de la frotación es:
(a) Inferior que la carga que existía antes.
(b) Igual a la carga que existía antes.
(c) Mayor que la carga que existía antes.
3. Una moneda de cobre (Z = 29) tiene una masa de 3 [g]. ¿Cuál es la carga total de
todos los electrones contenidos en la moneda?.
4. Tres cargas puntuales, q1 = 5 [µC ], q2 = −3 [µC ] y q3 = 10 [µC ], se colocan como se
muestra en la figura 5.17. Determine la fuerza resultante sobre la carga q3 .
84
Ejercicios propuestos electrostática.
Figura 1.56: (Problema 4).
5. Tres cargas puntuales q1 = 1, 5 [µC ], q2 = −3, 5 [µC ] y q3 = −3, 1 [µC ], se colocan en
las esquinas de un triángulo isósceles, como se muestra en la figura 3.21. Calcule la
fuerza eléctrica neta sobre la carga q1 .
Figura 1.57: (Problema 5).
6. Dos pequeñas esferas idénticas cargadas, cada una de ellas con una masa de
3 × 10−2 [kg], cuelgan en equilibrio como se ilustra en la figura 5.18. La longitud
de cada hilo es de 0, 15 [m] y el ángulo θ es de 5◦ . Encuentre la magnitud de la carga
de cada esfera.
Ejercicios propuestos electrostática.
85
Figura 1.58: (Problema 6).
7. Tres partículas separadas por una distancia d, se encuentran alineadas como se ilustra
en la figura 1.59. Las cargas q1 y q2 se mantienen fijas. La carga q3 tiene libertad de
movimiento pero, de hecho, permanece en reposo. ¿Cuál es la relación que existe entre
q1 y q2 ?.
Figura 1.59: (Problema 7 y 9).
8. Un cuerpo de 100 [kg] de masa está cargado con 1 [C ]. ¿A qué distancia sobre él debe
colocarse otro cuerpo cargado con 10 [C ] de signo contrario, para que el primero no
caiga por la acción de su propio peso?. Se supone que la experiencia se realiza en el
vacío.
9. Tres cargas puntuales q1 = 1 [µC ], q2 = −2 [µC ] y q1 = 3 [µC ], se encuentran alineadas
de tal forma que la segunda está situada en el centro de las otras dos. Si la separación
entre dos cargas consecutivas es 0,5 [m], calcular
(a) la energía potencial electrostática de cada carga debida a las otras,
(b) la energía potencial electrostática total del sistema.
10. En los vértices de un cuadrado de lado l existen cuatro cargas puntuales iguales con
carga q, y una carga −q en su centro. Hallar la energía potencial electrostática de
tal distribución.
Ejercicios propuestos electrostática.
86
11. Una carga positiva q1 = 8 [nC ] se encuentra en el origen y una segunda carga positiva
q1 = 12 [nC ] está sobre el eje x a una distancia a = 4 [m]. Determinar el campo
eléctrico resultante:
(a) En el punto P1 sobre el eje x en x = 7 [m],
(b) en el punto P2 sobre el eje x en x = 3 [m].
(c) Determinar el punto del eje x donde el campo eléctrico es cero.
12. Una carga puntual positiva de 10−2 [µC ] se encuentra en el punto A(−1, 2, −1) [m]. Otra
carga puntual negativa de −2 × 10−2 [µC ] se encuentra en B(2, −2, 2) [m]. Determinar
el campo eléctrico creado por esta distribución en el punto C (2, 4, 0) [m].
13. Tres cargas puntuales idénticas q, se localizan a lo largo de una circunferencia de
radio r en los ángulos 30◦ , 150◦ y 270◦ , como se muestra en la figura 1.60. ¿Cuál es el
campo eléctrico resultante en el centro del círculo?.
Figura 1.60: (Problema 13).
14. Cuatro cargas puntuales, q1 = 1, 5 [µC ], q2 = 1, 5 [µC ], q3 = 1, 5 [µC ], y q4 = 1, 5 [µC ],
se colocan en los vértices de un rectángulo, como muestra la figura 1.61. Calcule el
campo eléctrico en el centro del rectángulo.
Ejercicios propuestos electrostática.
87
Figura 1.61: (Problema 14).
15. Una carga +q se encuentra en x = a y una segunda carga −q en x = −a:
(a) Determinar el campo eléctrico sobre el eje x en un punto arbitrario x > a.
(b) Determinar la forma límite del campo eléctrico para x a.
16. Un dipolo eléctrico se define como una carga positiva q y una carga negativa −q
separadas por una distancia 2a. Para el dipolo del ejercicio anterior, determine el
~ debido a dicho dipolo, donde P está a una distancia y a del
campo eléctrico E
origen.
17. ¿Cuál de las siguientes afirmaciones acerca de las líneas de campo eléctrico asociadas
con cargas eléctricas es falsa?:
(a) Las líneas de campo eléctrico pueden ser rectas o curvas.
(b) Las líneas de campo eléctrico pueden formar lazos cerrados.
(c) Las líneas de campo eléctrico parten de cargas positivas y terminan en cargas
negativas.
(d) Las líneas de campo eléctrico jamás pueden cruzarse una con otra.
Ejercicios propuestos electrostática.
88
~ = 1000 [N/C ]ı̂ con una
18. Un electrón se proyecta en un campo eléctrico uniforme E
6
velocidad inicial ν~0 = 2 × 10 [m/s] en la dirección del campo. ¿Qué distancia recorrerá
el electrón antes de que momentáneamente quede en reposo?.
19. Una partícula tiene una carga positiva q, masa m, y una velocidad inicial ν0 . La
velocidad inicial forma un ángulo θ sobre la horizontal. La partícula entra en una
~ dirigido verticalmente hacia abajo,
región donde existe un campo eléctrico uniforme E
como se muestra en la figura 2.32. Despreciando la gravedad demuestre:
(a) El tiempo que le toma a la partícula regresar a la misma altura del punto donde
entró al campo eléctrico,
(b) la altura máxima alcanzada por la partícula,
(c) su desplazamiento horizontal cuando alcanza su altura máxima,
(d) el alcance horizontal de la partícula al regresar a la misma altura del punto donde
entró al campo.
Figura 1.62: (Problema 19).
20. Se lanzan protones con una velocidad inicial ν0 = 9, 55×103 [m/s] dentro de una región
~ = −720 [N/C ]̂, como se muestra en
donde el campo eléctrico uniforme presente es E
la figura 2.33. Los protones chocan en un blanco que se encuentra a una distancia
horizontal de 1, 27 [mm] del punto donde se lanzan los protones. Determine:
Ejercicios propuestos electrostática.
89
(a) Los dos ángulos θ de lanzamiento con que se dará en el blanco, y
(b) el tiempo total de vuelo para cada una de estas trayectorias.
Figura 1.63: (Problema 20).
21. Una varilla de longitud L como se muestra en la figura 2.34 tiene una carga positiva
uniforme por unidad de longitud λ y una carga total Q:
(a) Calcule el campo eléctrico en un punto P ubicado a lo largo del eje principal de
la varilla y a una distancia a de uno de sus extremos.
(b) Suponga que pasamos a un punto P muy alejado de la varilla. En este punto, ¿cuál
es la naturaleza del campo eléctrico?.
Figura 1.64: (Problema 21).
22. Dada la figura 2.35 y considerando la los datos del problema anterior:
Ejercicios propuestos electrostática.
90
(a) Calcule el campo eléctrico en un punto P(x, y) arbitrario.
(b) Aproxime su problema de modo que considere el campo eléctrico debido a una
carga lineal infinita.
Figura 1.65: (Problema 22).
23. Usando el resultado del problema anterior, obtener una expresión del campo eléctrico
a lo largo de la recta perpendicular bisectora (trazada desde el punto medio) debido
a la linea cargada con densidad de carga lineal uniforme λ y longitud L.
24. Considerar un segmento de recta cargado con una densidad lineal λ = 4,5 [nC /m]
localizado en el eje x entre x = −5 [cm] y x = +5 [cm] como se muestra en la figura
2.37. Utilizar la expresión de Ey obtenida en el problema anterior para calcular el
campo en el eje y en:
(a) y = 1 [cm],
(b) y = 4 [cm],
(c) y = 40 [cm].
(d) Calcular el campo eléctrico sobre el eje y para y = 1 [cm] suponiendo que la carga
lineal es infinita.
Ejercicios propuestos electrostática.
91
(e) Determinar la carga total y calcular el campo en y = 40 [cm], suponiendo que la
carga lineal se reduce a un punto.
Figura 1.66: (Problema 24).
25. Una linea cargada infinita de densidad lineal λ = 0, 6 [µC /m] está distribuida a lo
largo del eje z, y una carga puntual q = 8 [µC ] se encuentra sobre el eje y en y = 3 [m]
como se muestra en la figura 1.67. Determinar el campo eléctrico en el punto P del
eje x en x = 4 [m].
Figura 1.67: (Problema 25).
26. Un anillo de radio a tiene una carga total Q positiva distribuida de manera uniforme
como se muestra en la figura 1.68. Calcule el campo eléctrico generado por el anillo
en un punto P a una distancia x de su centro y a lo largo del eje central perpendicular
al plano del anillo.
92
Ejercicios propuestos electrostática.
Figura 1.68: (Problema 26).
27. Demuestre que la magnitud maxima del campo eléctrico a lo largo del eje de un anillo
√
cargado uniformemente ocurre cuando x = a/ 2 y tiene un valor de
Q
E= √
.
6 3πε0 a2
(1.150)
28. Un anillo de radio R se encuentra en el plano xy y una varilla en el eje z como
se muestra en la figura 1.69, ambos construidos con un hilo muy delgado, cargados
positiva y uniformemente con una densidad lineal de carga λ. Determinar la fuerza
que actúa sobre la varilla.
Figura 1.69: (Problema 28).
29. Un disco de radio R tiene una densidad de carga superficial uniforme σ . Calcule el
Ejercicios propuestos electrostática.
93
campo eléctrico en un punto P que está sobre el eje perpendicular al centro del disco
y a una distancia x del centro del mismo.
30. Considere un disco de radio R y densidad de carga σ . Demuestre que la intensidad
del campo eléctrico a lo largo del eje perpendicular al disco y a una distancia x del
centro (R x) se aproxima al de un plano infinito dado por E = σ /2ε0 .
31. Un hilo delgado posee una densidad de carga uniforme λ y está doblado en forma
de semicircunferencia de radio R. Calcular el módulo, dirección y sentido del campo
eléctrico en el centro de la semicircunferencia.
32. Un anillo de radio R está situado en el plano xy con su centro en el origen, y está
cargado con una densidad lineal de carga no uniforme λ = λ0 sin θ, de manera que en
el punto P(R, 0) tendremos λ = 0. Calcular la intensidad del campo electrostático en
el origen de coordenadas.
33. Un cono de base circular y radio a esta colocado de tal forma que su eje es horizontal.
~ se aplica en la dirección horizontal, como se muestra
Un campo eléctrico uniforme E
en la figura 4.38. Demuestre que el flujo eléctrico a través de la superficie cónica (sin
contar su base) está dado por πa2 E.
Figura 1.70: (Problema 33).
34. En un día claro, el campo eléctrico cerca de la superficie de la Tierra es
aproximadamente de 120 [N/C ] apuntando radialmente hacia adentro. Suponga que
el campo eléctrico tiene esta magnitud en toda la superficie de la Tierra. Determine
la carga total que podría estar almacenada en la Tierra en dicha situación. (R =
6, 37 × 106 [m]).
Ejercicios propuestos electrostática.
94
35. Mediante la aplicación de la Ley de Gauss, calcule la capacidad de:
(a) Dos láminas planas conductoras de área A separadas por una pequeña distancia d.
(b) Dos esferas concéntricas conductoras de radios a, b (b > a).
(c) Dos cilindros concéntricos conductores de longitud L, grande frente a ambos radios
a, b (b > a).
36. Una esfera sólida aislante de diámetro 28 [cm] tiene una densidad de carga uniforme
en todo su volumen. Si la magnitud del campo eléctrico a una distancia de 7[cm] desde
el centro es 5, 8 × 104 [N/C ], ¿cuál es la magnitud del campo eléctrico a 20 [cm] del
centro?.
37. Una distribución de carga esféricamente simétrica, de radio R, tiene una densidad de
carga dada por ρ = a/r, donde a es una constante. Encuentre la intensidad del campo
eléctrico como una función de r.
38. La figura 1.71 muestra una esfera aislante de radio a concéntrica a un cascarón
esférico aislante de radio interior b y radio exterior c. Si la esfera tiene una carga
total Q uniformemente distribuida en su volumen, y el cascarón tiene una carga −Q
uniformemente distribuido en el cascarón. Determinar el campo eléctrico:
(a) Dentro de la esfera (r < a),
(b) entre la esfera y el cascarón (a < r < b),
(c) en el cascarón (b < r < c),
(d) fuera del cascarón (r > c).
Ejercicios propuestos electrostática.
95
Figura 1.71: (Problema 38 y 56).
39. Un hilo recto y muy largo tiene una densidad de carga lineal de 6 [µC /m]. Determinar
la intensidad del campo eléctrico en las siguientes distancia del hilo:
(a) 5 [cm],
(b) 30 [cm] y
(c) 200 [cm].
40. Dos alambres largos, rectos y paralelos tiene cargas por unidad de longitud de λ1 y
λ2 . La separación entre sus ejes es b, como se muestra en la figura 1.72. Encuentre la
magnitud de la fuerza por unidad de longitud ejercida sobre un alambre causada por
la carga del otro.
Figura 1.72: (Problema 40).
41. Calcular la intensidad del campo eléctrico creado por un volumen cilíndrico muy largo
de radio R, en que se halla distribuida uniformemente una carga positiva, conociendo
Ejercicios propuestos electrostática.
96
la carga por unidad de volumen ρ, en puntos situados a una distancia r del eje en los
casos siguientes:
(a) r < R y
(b) r > R.
42. Calcular la intensidad del campo eléctrico creado por una placa delgada, indefinida y
uniformemente cargada con una densidad superficial de carga σ , en un punto fuera de
ella.
43. Calcule la divergencia de ~r = xı̂ + y̂ + z k̂.
44. Consideremos una carga puntual q en el origen. Excepto donde se encuentra
posicionada la carga, la densidad de carga es cero, de forma que la divergencia del
campo eléctrico debe ser cero. Verifique este resultado.
45. Vamos a recordar conceptos matemáticos básicos.
(a) Calcule el gradiente de la función. Discuta el significado de gradiente.
~ = xyzı̂ + y2 x̂ − y3 (z 2 − 1)k̂. Discuta sobre el
(b) Calcule la divergencia del vector A
significado de divergencia.
~ = (xz − 2x)ı̂ + xz̂ + xyk̂. ser un campo electrostático?. Explique
(c) ¿Puede el vector E
la condición que aplicó para resolver el problema.
(d) Calcule el trabajo realizado al mover una carga puntual de 10 [µC ] desde (0, 0, 0)
hasta el punto (3, 2, 0) en la presencia del campo eléctrico definido en (c).
46. Una placa circular de radio 80[cm] descargada se coloca en un campo eléctrico intenso
de 27 × 104 [N/C ]. La dirección de la intensidad del campo eléctrico es perpendicular
a la placa. Determine:
(a) La densidad de carga inducida en cada cara de la placa,
(b) la carga total inducida en cada cara.
Ejercicios propuestos electrostática.
97
47. Un cascarón esférico conductor delgado de radio 30 [cm] tiene una carga neta de
−14, 5 [µC ] uniformemente distribuida en su superficie. Determine la intensidad del
campo eléctrico dentro y fuera del cascarón.
~ = 8 × 104 ı̂. El protón
48. Un protón se libera del reposo en un campo eléctrico uniforme E
sufre un desplazamiento de 0, 5 [m] en la dirección del campo.
(a) Encuentre el cambio en el potencial eléctrico entre el punto en que el protón se
libera del reposo y el punto después de recorrer los 0, 5 [m].
(b) Determine el cambio en la energía potencial del sistema para este desplazamiento.
(c) Determine la velocidad del protón después de completar el desplazamiento de
0, 5 [m] en el campo eléctrico.
49. Obtener una expresión para VA − VB de la configuración de cargas mostrado en la
figura 1.73.
Figura 1.73: (Problema 49).
50. Un dipolo eléctrico consiste de dos cargas de magnitud equivalente y de signo opuesto,
separadas por una distancia 2a. El dipolo se encuentra a lo largo del eje x y su centro
está en el origen.
(a) Calcule el potencial eléctrico en el punto P.
(b) Calcule el potencial eléctrico y el campo eléctrico (usando gradiente) en un punto
alejado del dipolo (x a).
51. Una carga cuya densidad lineal esta determinada por λ = βx, donde β es una
constante positiva, está distribuida sobre una varilla delgada de longitud L que se
encuentra sobre el eje x con uno de sus extremos en el origen, como se muestra en la
figura 1.74.
Ejercicios propuestos electrostática.
98
(a) ¿Cuáles son las unidades de la constante β?.
(b) Calcule el potencial eléctrico en el punto A y B.
Figura 1.74: (Problema 51).
52. El potencial eléctrico en cierta región del espacio está dado or V = −83x 2 z + 13yx 3 +
90yz 2 [V ].
(a) Encuentre la intensidad del campo eléctrico.
(b) Calcule las componentes del campo eléctrico en el punto (−1, 6, 9) donde todas las
distancias están en metros.
53. Una esfera sólida aislante de radio R tiene una densidad de carga volumétrica positiva
uniforme y carga total Q.
(a) Determine el potencial eléctrico en un punto fuera de la esfera, esto es, para r > R.
(b) Determine el potencial en un punto en el interior de la esfera, esto es, para r < R.
54. Una esfera sólida metálica de radio a con una carga Q está en el centro de un cascarón
esférico metálico de radio interno b y radio externo c con una carga neta igual a cero,
como se muestra en la figura 1.75. Encuentre el potencial eléctrico en:
(a) r > c,
Ejercicios propuestos electrostática.
99
(b) b < r < c,
(c) a < r < b,
(d) r < a.
(e) Realice una gráfica de V versus r.
Figura 1.75: (Problema 54 y 55).
55. Repita el ejercicio anterior si el cascarón tiene una carga neta −Q.
56. Una esfera sólida aislante de radio a con una carga Q está en el centro de un cascarón
esférico metálico de radio interno b y radio externo c con una carga neta −Q, como
se muestra en la figura 1.71. Encuentre el potencial eléctrico en:
(a) r > c,
(b) b < r < c,
(c) a < r < b,
(d) r < a.
(e) Realice una gráfica de V versus r.
Ejercicios propuestos electrostática.
100
57. Un conductor esférico de radio a tiene una densidad superficial de carga σa ; se
encuentra en el interior de una esfera también conductora y hueca de radios interior
y exterior b y c, respectivamente, estando ésta última conectada a tierra a través de
una batería de tensión V0 . Encuentre:
(a) Las densidades superficiales de carga sobre la superficie exterior e interior de la
esfera hueca.
La expresión del campo y el potencial a una distancia r del centro de las esferas,
cuando:
(b) r > c,
(c) c > r > b,
(d) b > r > a y
(e) en r < a.
~ = (xz − 2x)ı̂ + xz̂ + xyk̂ ser un campo electrostático?.
58. ¿Puede el vector E
59. Demuestre que las placas paralelas de un condensador se atraen con una fuerza dada
por la expresión
F=
Q2
2ε0 A
(1.151)
Sugerencia: Calcule el trabajo para aumentar la separación entre las placas de x hasta
x + dx. Así, el trabajo realizado en separar las placas cargadas es W = F dx.
60. Un capacitor cilíndrico tiene conductores interno y externo cuyos radios tienen una
razón b/a = 5/3, como se muestra en la figura 1.76. El conductor interno se reemplaza
por un alambre cuyo radio es la mitad del radio del conductor original. ¿Porque factor
debería incrementar la longitud del capacitor para que tuviese la capacitancia del
capacitor original?.
Ejercicios propuestos electrostática.
101
Figura 1.76: (Problema 60).
61. Dos cascarones esféricos concéntricos forman un capacitor de 4[nF ]. Si el radio externo
del cascarón menor es de 42 [cm], ¿cuál es el valor del radio del cascarón mayor?.
62. Considere un grupo de capacitores que se observa en la figura 1.77.
(a) Encuentre la capacitancia equivalente entre los puntos a y b.
(b) Calcule la carga en cada capacitor cuando la diferencia de potencial entre a y b
es 9 [V ].
Figura 1.77: (Problema 62).
63. Calcule la capacitancia equivalente entre los puntos a y b del grupo de capacitores
que se muestran en la figura 1.78.
102
Ejercicios propuestos electrostática.
Figura 1.78: (Problema 63).
64. Considere un capacitor con placas paralelas cuya área es 16 [cm2 ] y tiene una
capacitancia de 88 [µF ]. Si existe una diferencia de potencial de 15 [V ] entre sus placas,
(a) Calcule la energía almacenada en el capacitor.
(b) Calcule la densidad de energía (energía por unidad de volumen) en el campo
eléctrico del capacitor si las placas están separadas por aire.
65. Utilice la ecuación de la densidad de energía en un campo eléctrico para hacer el
cálculo explícito de la energía almacenada en el campo eléctrico de un capacitor
esférico simple. Demuestre que
q2
.
(1.152)
U=
2C
66. Las placas cuadradas de un condensador, cada una de lado a, forman un ángulo θ
entre sí, como se ilustra en la figura 1.79.
Figura 1.79: (Problema 66).
Ejercicios propuestos electrostática.
Demostrar que cuando θ es pequeño, la capacitancia es
ε0 a2
aθ
C=
1−
.
d
2d
103
(1.153)
104
Ejercicios propuestos electrostática.
Capítulo 2
Transporte eléctrico
ara crear una corriente eléctrica en un alambre de cobre, se necesita una carga
positiva en un extremo y una carga negativa en el otro. Históricamente, se elaboraron
dos teorías de la corriente eléctrica: La teoría convencional es la más antigua de las dos
y establece que la corriente fluye de una carga positiva a una negativa. La teoría del
electrón indica que la corriente fluye de una carga negativa a una positiva.
P
Este hecho, en principio contradictorio, se debe a razones históricas. Las teorías
básicas que explican el funcionamiento de la electricidad, son anteriores al conocimiento
de la existencia de los electrones. En todas estas teorías y estudios iniciales se toma,
por convenio, que éste era el sentido de circulación de la corriente eléctrica.
2.1.
Corriente eléctrica
2.1.1.
Transporte de carga y densidad de corriente
Las corrientes eléctricas se deben al movimiento de portadores de carga. La corriente
eléctrica en un hilo es la medida de la cantidad de carga que pasa a través de un punto
del hilo por unidad de tiempo.
1C
∆Q
(1A) =
(2.1)
I=
∆t
1s
La corriente de un Ampere equivale a 6, 2 · 1018 electrones por segundo.
Importante Lo que cuenta es siempre el transporte de carga neto, con la debida
106
2.1. Corriente eléctrica
consideración al signo. El movimiento de un cuerpo neutro supone el transporte de una
gran cantidad de carga, pero no hay corriente debido a que se mueven exactamente el
mismo número de cargas positivas que negativas con la misma velocidad media.
Es convencional asignar a la corriente la misma dirección que el flujo de carga positiva.
Para describir el transporte de carga en un volumen tridimensional, usaremos el concepto
de densidad de corriente. Vamos a considerar valores medios de las magnitudes. Además,
consideraremos que nuestra escala de distancias es tal que en toda pequeña región existe
un gran número de partículas.
Supongamos un sistema donde, en promedio, hay n partículas por cm3 moviéndose
todas con el mismo vector velocidad ν~ y transportando la misma carga q. Imaginemos un
~ fijo con cierta orientación. ¿Cuantas partículas atraviesan el cuadro en
cuadro de área a
un tiempo ∆t?
Figura 2.1: Cargas en movimiento a través de un rectángulo de área a.
Las partículas destinadas a atravesar el cuadro en los próximos ∆t segundos serán
las que están ahora en el prisma oblicuo. El cuadro es la base del prisma y la longitud
de su arista es ν∆t, que es la distancia que recorre una partícula en un tiempo ∆t. Las
partículas fuera del prisma no alcanzan o no aciertan a la ventana.
2.1. Corriente eléctrica
107
Figura 2.2: Cargas en movimiento que atraviesan un prisma en un
intervalo ∆t.
~ · ν~ ∆t. En promedio, el número de
El volumen del prisma es V = aν∆t cos θ = a
partículas que se encuentran en este volumen es n~
a · ν~ ∆t. De este modo, la corriente a
través del cuadro (valor medio de la carga que atraviesa el cuadro por unidad de tiempo)
es
q(n~
a · ν~ ∆t)
= nq~
a · ν~ .
(2.2)
I(a) =
∆t
Supongamos ahora que tenemos distintas partículas, que difieren en la carga y en el
vector velocidad. Denotando cada clase por el sub-índice k, la k-ésima partícula tiene
una carga qk en cada partícula, se mueve con velocidad ν~k , y está presente con una
concentración media de nk partículas por cm3 , lo que da
~ · ν~1 + n2 q2 a
~ · ν~2 + . . . = a
~·
I(a) = n1 q1 a
X
nk qk ν~k .
(2.3)
k
~ le llamamos densidad de corriente ~J
A la magnitud vectorial que multiplica el área a
X
A
~J =
.
(2.4)
nk qk ν~k
cm2
k
Ahora, en un conductor, los electrones tienen una distribución de velocidades casi al
azar, que varían considerablemente en módulo y dirección. Sea ne el número de electrones
2.1. Corriente eléctrica
108
por unidad de volumen de todas las velocidades, podemos dividir los electrones en grupos,
cada uno de los cuales contiene electrones con casi la misma celeridad y dirección.
La velocidad media de todos los electrones se calcula sumando cada grupo
ponderando cada velocidad por el número de electrones en el grupo, y dividiendo por el
número total de electrones
1 X
ν~m =
nk ν~k .
(2.5)
ne
k
Recordando que para el electrón tenemos que la carga q = −e, entonces
~Je = −e
X
nk ν~k = −ene ν~m .
(2.6)
k
La corriente a través del cuadro depende sólo de la velocidad media de los portadores
de carga.
2.1.2.
Corrientes estacionarias
La corriente I que circula a través de cualquier superficie S es precisamente la integral
de superficie
Z
~
I = ~J · dS.
(2.7)
s
Hablamos de un sistema de corriente estacionaria cuando el vector densidad de
corriente ~J permanece constante con el tiempo en todo punto. Las corrientes estacionarias
deben obedecer a la ley de conservación de la carga.
Si los portadores de carga positivos salen de la superficie, la carga dentro de la
superficie se agota, y ~J dejará de ser constante. La solución es que se cree carga en el
interior de la superficie, pero esto viola la ley de conservación de la carga
I
s
~J · dS
~=
Z
V
~ · ~Jdν ⇒ ∇
~ · ~J = 0
∇
(corrientes estacionarias).
(2.8)
2.1. Corriente eléctrica
109
Supongamos que la corriente ahora no es estacionaria, siendo ~J función del tiempo
I
Z
~J · dS
~ = − dq = − d
ρdν
(2.9)
dt
dt v
s
I
Z
Z
~J · dS
~=
~ · ~Jdν = − d
∇
ρdν
(2.10)
dt v
s
V
~ · ~J = − ∂ρ
∇
(corriente no estacionarias))
(2.11)
∂t
Ambas ecuaciones expresan la conservación de la carga: no puede salir carga de un
lugar sin disminuir la cantidad de carga allí existente.
2.1.2.1.
Ejercicio
La cantidad de carga q que pasa a través de una superficie de área 1 [mm2 ] varía con
el tiempo de acuerdo con la expresión q(t) = 4t 3 − 6t 2 + 6.
Solución
(a) ¿Cuál es la intensidad de corriente instantánea a través de la superficie en t = 2 [s]?.
d
dq(t)
=
(4t 3 − 6t 2 + 6) = 12t 2 − 12t
dt
dt
⇒ I(2[s]) = 12(2)2 − 12(2) = 24 [A]
I(t) =
(b) ¿Cuál es el valor de la densidad de corriente?
Z
Z
~ = I = ~J dS =J(t)S
I(t) = ~J · dS
s
s
I(t)
12t 2 − 12t
=
S
S
12(2[s])2 − 12(2[s])
A
6
⇒J(2[s]) =
= 24 · 10
−6
10
m2
J(t) =
(c) ¿En qué instante alcanza la mínima intensidad de corriente instantánea?
I(t) = 12t 2 − 12t
∂I(t)
∂
= (12t 2 − 12t) = 14t − 12 = 0 ⇒ t = 0, 5 [s]
∂t
∂t
∂2 I(t)
= 24 > 0
por lo que corresponde a un mínimo.
∂t 2
2.2. Ley de Ohm
110
2.1.2.2.
Ejercicio
Por un alambre de cobre de 2, 54 [mm] de diámetro circula una corriente de 0, 5 [A].
Calcule la velocidad media de los electrones. Suponga que la concentración de electrones
libres es 8 · 1028 [electrones/m3 ].
Solución
La densidad de corriente está dada por J = I/A = nqVp , de modo que
Vp =
I
I
=
nqA
nqπ
h i
4I
−6 m
=
7,
71
·
10
=
D 2
s
nqπD 2
2
2.2.
Ley de Ohm
2.2.1.
Conductividad eléctrica y Ley de Ohm
En clases pasadas se llegó a la conclusión de que el campo eléctrico en el interior
de un conductor es igual a cero, afirmación sólo cierta si el conductor está en equilibrio
electrostático. Cuando las cargas no están en equilibrio existe un campo eléctrico en el
conductor.
En un conductor, siempre que se mantenga una diferencia de potencial en él, se
~ En algunos materiales,
establecerá una densidad de corriente ~J y un campo eléctrico E.
la densidad de corriente es proporcional al campo eléctrico
~J = σ E
~
σ : conductividad eléctrica.
(2.12)
Los materiales que obedecen la ecuación anterior se dice que siguen la Ley de Ohm, en
honor a Georg Simon Ohm (1789-1854). La ley de Ohm afirma que en muchos materiales
(incluyendo la mayor parte de los metales) la relación de la densidad de corriente ~J con
~ es una constante σ que es independiente del campo eléctrico que
el campo eléctrico E
produce la corriente.
2.2. Ley de Ohm
111
Figura 2.3: Sección de un alambre portador de corriente.
De un extremo al otro del alambre se mantiene una diferencia de potencial ∆V =
VB −VA , lo que genera en el alambre un campo electrostático y una corriente. Si el campo
eléctrico es uniforme, entonces
B
Z
∆V = −
A
~ · d~l = E
E
Z
L
0
dx = EL,
(2.13)
por lo tanto, podemos expresar la magnitud de la densidad de corriente en el alambre
como
∆V
J = σE = σ
,
(2.14)
L
ahora, dado que
Z
I=
S
~J · dS
~ =J
Z
S
dS = JA,
(2.15)
entonces podemos escribir la diferencia de potencial como
L
∆V = J =
σ
L
σA
I =RI
⇒R =
(2.16)
L
σA
resistencia del conductor.
(2.17)
Podemos definir la resistencia como la relación existente entre la diferencia de
potencial aplicada a un conductor y la corriente que pasa por el mismo
∆V
L
R=
=
I
σA
1V
(1[Ω]) =
.
1A
(2.18)
2.2. Ley de Ohm
112
El recíproco de la conductividad es la resistividad ρ = 1/σ [Ωm]. De manera que

 ρcobre = 1, 7 · 10−8 [Ω · m]
L 
R =ρ
(2.19)
ρsilicio = 640 [Ω · m]
A 

10
14
ρvidrio = 10 − 10 [Ω · m]
(a) Material Óhmico
(b) Material no Óhmico
Figura 2.4: Gráficos de corriente I en función del voltaje V, para
materiales óhmicos y no óhmicos
2.2.1.1.
Ejemplo
Por un alambre de radio uniforme de 0, 26 [cm] fluye una corriente de 10 [A] producida
por un campo eléctrico de magnitud 110 [V /m]. ¿Cuál es la resistividad del material?
Solución
La resistencia eléctrica está dada por
R=
Lρ
V
=
A
I
La diferencia de potencial entre los bordes del alambre está dada por
V =
E
L
De este modo tendremos que
R =ρ
L
EL
EA
πr 2 E
=
⇒ ρ=
=
= 233, 61 [µΩm]
A
I
I
I
2.2. Ley de Ohm
2.2.1.2.
113
Ejemplo
Los cables coaxiales se utilizan ampliamente para la televisión por cable, entre
otras aplicaciones electrónicas. Un cable coaxial está constituido por dos conductores
cilíndricos concéntricos. La región entre los conductores está totalmente llena de silicio.
La fuga de corriente a través del silicio, en la dirección radial, no es deseada. El radio del
conductor interno es a = 0, 5 [cm] y el radio externo es b = 1, 75 [cm], siendo la longitud
L = 15 [cm]. Calcule la resistencia del silicio entre los conductores.
Solución
Mediante la Ley de Gauss tenemos
I
~ · dS
~ = qint
E
ε0
s
I
Lλ
E dS =
ε0
s
Lλ
E(2πrL) =
ε0
2kλ
~=
⇒ E
r̂
r
⇒
⇒
La diferencia de potencial es
Z
∆V = Vb − Va = −
b
⇒ V = 2kλ ln
a
b
a
~ · dS
~ = −2kλ
E
Z
b
a
dr
= −2kλ ln
r
Pero
V = IR
⇒ R=
de modo que
V
V
V
=
=
I
JA
σ EA
2kλ ln ab
V
ρ
b
R=
=
= 2kλ
ln
σ EA
2πL
a
r σ (2πrL)
Otra opción es tomar el diferencial
dR =
ρ
ρ
dr =
dr
A
2πrL
b
a
2.2. Ley de Ohm
114
De esta forma tendremos que
Z
R=
b
a
ρ
dR =
2πL
Z
b
a
dr
ρ
=
ln
r
2πL
b
a
Reemplazando en esta ecuación los valores dados, y conociendo que ρsi = 640 [Ωm],
entonces
b
ρ
= 851 [Ω]
ln
R=
2πL
a
Vamos a comparar esta resistencia con la del conductor interno del cable en un tramo
de 15 [cm]. Suponiendo que el conductor está hecho de cobre, ρcu = 1, 7 · 10−8 [Ωm],
tendremos
ρ
b
R = ln
= 3, 2 · 10−5 [Ω]
A
a
Esta resistencia es mucho menor que la resistencia radial. Así, prácticamente toda la
corriente corresponde a cargas moviéndose a lo largo del cable, y una fracción muy
pequeña se fuga en la dirección radial.
2.2.1.3.
Ejemplo
Un alambre tiene forma de cono circular truncado. Los radios de los extremos son r1 y
r2 , y el largo es L. Si la abertura es pequeña, encontrar una expresión para la resistencia
entre los extremos del alambre.
Figura 2.5: Cono circular truncado.
Solución
2.2. Ley de Ohm
115
Considerando un diferencial de cono de radio r y longitud dx, la diferencial de
resistencia será
dx
dR = ρ 2
πr
Para expresar el radio como función de x, se calcula la ecuación de la recta
r2 − r1
r(x) =
x + r1
L
Integrando tendremos que:
Z
dx
ρ L
L
R=
=ρ
π 0 r1 + r2 −r2 x 2
πr1 r2
L
Z
dx
1
Donde hemos usado que
=−
.
b(bx + a)
(a + bx)2
2.2.2.
Modelo de conducción eléctrica
Pensemos en un conductor como un arreglo de átomos con un conjunto de electrones
libres (electrones de conducción). Los electrones de conducción obtienen movilidad cuando
los átomos libres se condensan en un sólido. En ausencia de un campo eléctrico, los
electrones de conducción se mueven al azar a través del conductor con velocidades
promedio del orden de los 106 [m/s].
En ausencia de campo no existe corriente eléctrica en un conductor dado que la
velocidad media de los electrones libres es igual a cero. Esto es, en promedio, se mueven
tantos electrones en una dirección como en la dirección contraria, y por lo tanto, no se
presenta un flujo neto de cargas
Figura 2.6: Movimiento aleatorio de un portador de carga en un
conductor en ausencia de campo eléctrico.
2.2. Ley de Ohm
116
Diferente es cuando se aplica un campo eléctrico. En este caso, además de
experimentar el movimiento aleatorio, los electrones libres derivan lentamente en
dirección opuesta a la del campo eléctrico, con una velocidad media mucho menor
(10−4 [m/s]) que sus velocidades promedio entre las colisiones (106 [m/s]).
Figura 2.7: Movimiento aleatorio de un portador de carga en un
conductor, en presencia de campo eléctrico.
En nuestro modelo suponemos que el movimiento de un electrón después de una
colisión es independiente de su movimiento antes de la misma. Además, la energía
adicional adquirida por los electrones en el campo eléctrico se pierde hacia los átomos
del conductor cuando entran en colisión los electrones y los átomos. Así, la energía
transmitida a los átomos incrementa su energía vibratoria, aumentando entonces la
temperatura del conductor
~ = m~
F~ = qE
a
~=
a
(2.20)
~
eE
.
m
(2.21)
Esta aceleración, que ocurre sólo durante un corto intervalo de tiempo entre las
colisiones, le permite al electrón adquirir una pequeña velocidad de arrastre (velocidad
media).
Si definimos t = 0 como el instante siguiente después de una colisión, y t al momento
en que ocurre la siguiente colisión, entonces
~ t = ν~i +
ν~f = ν~i + a
~
qE
t
m
(2.22)
2.2. Ley de Ohm
117
Figura 2.8: Instante entre colisiones.
Si suponemos que las velocidades iniciales están distribuidas en forma aleatoria,
entonces el valor promedio será ν~i = 0. El valor promedio del segundo término de la
~
ecuación anterior es (qE/m)τ,
donde τ es el intervalo de tiempo promedio entre colisiones
sucesivas. Dado que el valor promedio de ν~f es igual a la velocidad media ν~m entonces
qτ ~
ν~m =
E.
(2.23)
m
Recordando la definición de densidad de corriente tendremos que
nq2 τ ~
~j = nq~
νm =
E.
m
(2.24)
Usando la ley de Ohm
2
~
~J = σ E
~ = nq τ E,
m
tendremos que la conductividad y resistividad de un conductor es
nq2 τ
m
1
m ~
ρ= =
E.
σ
nq2 τ
σ=
(2.25)
(2.26)
(2.27)
El intervalo de tiempo promedio τ entre colisiones sucesivas esta relacionado con la
distancia promedio entre colisiones l (trayectoria libre media) y la velocidad promedio ν̄:
τ=
2.2.3.
l
ν̄
(2.28)
Resistencia y temperatura
En un rango limitado de temperatura, la resistividad de un conductor varía
prácticamente de manera lineal en función de la temperatura
ρ = ρ0 (1 + α(T − T0 )),
(2.29)
2.2. Ley de Ohm
118
donde ρ es la resistividad a cierta temperatura, ρ0 es la resistividad a alguna temperatura
de referencia T0 , y α es el coeficiente de temperatura de resistividad.
ρ = ρ0 + ρ0 α(T − T0 )
ρ − ρ0 = ρ0 α(T − T0 )
⇒ α=
∆ρ
ρ − ρ0
=
,
ρ0 (T − T0 )
ρ0 ∆T
(2.30)
(2.31)
(2.32)
siendo ∆ρ = ρ − ρ0 el cambio en la resistividad durante el cambio de temperatura
∆T = T − T0 .
Material
α ( ◦C )
Plata
3, 8 · 10−3
cobre
3, 9 · 10−3
Platino
3, 92 · 10−3
Oro
3, 4 · 10−3
Silicio
−75 · 10−3
Cuadro 2.1: coeficientes α (temperatura de resistividad) para distintos
metales.
Como la resistencia es proporcional a la resistividad, entonces
R = R0 (1 + α(T − T0 )).
(2.33)
El uso de esta propiedad nos permite realizar mediciones precisas de la temperatura
midiendo cambios en la resistencia del material.
2.2.3.1.
Ejemplo
Un termómetro para resistencias, que mide la temperatura al determinar el cambio en
la resistencia de un conductor, esta hecho de platino y tiene una resistencia de 50 [ω] a
20 [◦ C ]. Cuando se le sumerge en un recipiente que contiene indio fundido, su resistencia
aumenta a 76, 8 [ω]. Calcule el punto de fusion del indio.
2.2. Ley de Ohm
119
Solución
R = R0 (1 + α(T − T0 ))
⇒
R − R0 = R0 α(T − T0 ) = R0 α∆T
∆T = T − T0 =
⇒
R − R0
= 137◦ C
αR0
T = 137◦ C + T0 = 137◦ C + 20◦ C = 157◦ C
Para metales como el cobre, la resistividad es prácticamente proporcional a la
temperatura. Sin embargo, a muy bajas temperaturas siempre existe una región no lineal y
la resistividad alcanza un valor finito conforme la temperatura se acerca al cero absoluto.
Esta resistividad residual está causada principalmente por la colisión de electrones
con impurezas y con imperfecciones en el metal. Por otro lado, la resistividad a altas
temperaturas (región lineal) se debe a las colisiones entre los electrones y los átomos
metálicos.
(a) Metal
(b) Semicondutor
Figura 2.9: Gráfico de resistividad ρ en función de la temperatura T .
Es importante señalar que los semiconductores presentan valores de α (coeficiente
entre temperatura y resistividad) negativos, es decir, la resistividad disminuye con el
aumento de la temperatura. Esto se debe a un aumento en la densidad de los portadores
de carga a temperaturas elevadas. Los portadores de carga se asocian con impurezas
atómicas.
2.2. Ley de Ohm
120
2.2.4.
Superconductores
Los superconductores son aquellos materiales que reducen su resistencia hasta cero
cuando llegan a una cierta temperatura Tc conocida como temperatura crítica. Este
fenómeno fue descubierto en 1911 por el físico holandés Heike Kamerlingh-Onnes (18531926) mientras trabajaba con mercurio.
Figura 2.10: Gráfico de la resistencia del mercurio en función de la
temperartura.
Las resistividades de los superconductores son inferiores a 4 · 10−25 [Ωm], alrededor
de 1017 veces menor que la resistividad del cobre. Los superconductores se clasifican en:
Materiales cerámicos de altas temperaturas críticas
Materiales superconductores metálicos
Material
Tc [◦ K ]
HgBa2 Ca2 Cu3 O8
134
YBa2 Cu3 O7
92
Nb
9,46
Pb
7,18
Hg
4,15
Al
1,19
Cuadro 2.2: Materiales superconductores
2.2. Ley de Ohm
121
Si llegase a identificarse un superconductor a la temperatura ambiente, su impacto
sobre la tecnología sería tremendo. El valor de Tc es sensible a la composición química,
a la presión, y a la estructura molecular del material.
Una vez que se ha establecido en un superconductor una corriente, persiste sin
necesidad de una diferencia de potencial aplicado (R = 0 (Ω)).
Aplicación: Imanes superconductores, donde la magnitud del campo magnético es 10
veces mayor que la de los electroimanes normales.
2.2.5.
Potencia eléctrica
En los circuitos eléctricos típicos, la energía se transfiere de una fuente (una batería)
a algún dispositivo (ampolleta).
Figura 2.11: Circuito eléctrico simple, formado por una batería (∆V ),
una resistencia (R) y cables de conexión.
En este circuito podemos pensar que se está entregando energía a un resistor. Dado
que los alambres también tiene resistencia, parte de la energía es entregada a los
alambres y parte a la resistencia. Supondremos que la resistencia de los alambres es
tan pequeña en comparación con la resistencia del circuito, que ignoraremos la energía
suministrada a los alambres.
A medida que una carga Q positiva se mueves desde a hasta b a través de la batería,
la energía potencial eléctrica del sistema aumenta en un valor Q∆V , en tanto que la
energía potencial química de la batería se reduce en la misma cantidad
∆U = Q∆V .
(2.34)
2.2. Ley de Ohm
122
Sin embargo, a medida que la carga se mueve desde c hasta d a través del resistor,
el sistema pierde esta energía potencial eléctrica durante las colisiones de los electrones
con átomos del resistor. En este proceso la energía se transforma en energía interna que
corresponde a un incremento en el movimiento de vibración de los átomos en el resistor.
Cuando la carga regresa al punto a
Energía Química → Resistor → Vibración Moléculas (Calor)
Consideremos ahora la velocidad a la cual el sistema pierde energía potencial
eléctrica conforme la carga Q pasa a través de la resistencia
P≡
dU
d(Q∆V )
=
= I∆V ,
dt
dt
(2.35)
donde P se define como la potencia, que representa la rapidez a la cual se entrega
energía a la resistencia. Como ∆V = IR entonces
P = I∆V = I 2 R =
(∆V )2
R
[Watts].
(2.36)
Las líneas de transmisión verdaderas efectivamente tienen resistencia, y se entrega
potencia a la resistencia de esos alambres. Las compañías eléctricas buscan minimizar
la potencia transformada en energía interna en las líneas y maximizar la energía
transformada al consumidor. Como el cobre es caro, usan cables con una menor sección
transversal y así, con una mayor resistencia
R =ρ
L
A
A pequeño → R grande,
(2.37)
pero como la potencia es
P = I 2 R = I∆V ,
(2.38)
entonces como la resistencia es grande, usan una corriente pequeña para que la potencia
suministrada a los cables no sea tan elevada. Pero para mantener una corriente pequeña,
deben transferir la energía a un voltaje elevado. En algunos sitios, la potencia es
transportada a diferencias de potencial de 765[kV ] o más. Una vez que la electricidad llega
a la ciudad, la diferencia de potencial se reduce a 4 [kV ] mediante un transformador. Otro
transformador reduce el potencial hasta 220 [V ] antes de que finalmente la electricidad
llegue a su hogar. Cada vez que se reduce el potencial, la corriente aumenta en el mismo
factor, conservándose la misma potencia.
2.3. Circuitos
2.2.5.1.
123
Ejemplo
Una lámpara eléctrica de 10 [Ω] se etiqueta a 100 [W ] (maxima potencia permitida).
¿Cual es el máximo voltaje de operación que soportaría?.
Solución
P = IV =
2.2.5.2.
V2
R
⇒V =
√
PR = 31, 62 [V ]
Ejemplo
Un calentador eléctrico funcíona aplicando una diferencia de potencial de 120 [V ] a
un alambre de Nicromo que tiene una resistencia total de 8 [Ω]. Determine la corriente
que pasa por el alambre y la potencia nominal del calentador.
Solución
V
= 15 [A]
R
P = I 2 R = 1800 [W ]
V = IR
2.3.
⇒I=
Circuitos
a sabemos que las cargas se mueven por la diferencia de potencial que produce una
batería. Como la diferencia de potencial es constante, también la corriente en el
circuito es constante en magnitud y dirección, y recibe el nombre de corriente directa.
Y
2.3.1.
Fuerza electromotriz
La bateria se conoce como una fuente de fuerza electromotriz (fem). La fem ε de una
batería es el voltaje máximo posible que está puede suministrar entre sus terminales.
La terminal positiva de la batería se encuentra a un potencial más alto que la negativa.
Debido a que una batería verdadera está hecha de materia, existe una resistencia al flujo
de las cargas dentro de la batería. Esta resistencia se conoce como resistencia interna r.
2.3. Circuitos
124
Figura 2.12: Circuito de una fuente de fem ε de resistencia interna r
conectada a una resistencia externa R.
Conforme pasamos de la terminal negativa a la positiva, el potencial aumenta en una
cantidad ε. Sin embargo, a medida que nos movemos a través de la resistencia r, el
potencial disminuye en una cantidad Ir
∆V = Vb − Va = ε − Ir,
(2.39)
ε es el voltaje en circuito abierto, es decir, el voltaje terminal cuando la corriente es
igual a cero. Por ejemplo, una pila tiene una fem de 1,5 [V ]. La diferencia de potencial
real depende de la corriente. El voltaje terminal ∆V debe ser igual a la diferencia de
potencial entre los extremos de la resistencia externa R, conocida como resistencia de
carga
(
∆V = IR
∆V = ε − Ir
ε = Ir + IR ⇒ I =
ε
ε
ε
≈ ,
=
r
R +r
R
R 1+ R
(2.40)
si multiplicamos la ecuación anterior por la corriente tendremos
P = Iε = I 2 R + I 2 r.
(2.41)
2.3. Circuitos
125
Figura 2.13: variación del potencial en el circuito en serie de a hasta
d.
2.3.1.1.
Ejemplo
Una batería tiene una fem de 30[V ]. El voltaje en las terminales de la batería disminuye
a 24 [V ] cuando se disipan 25 [W ] de potencia en un resistor externo R.
(a) ¿Cuál es el valor de R?
P = IV =
V2
V2
⇒ R=
= 23, 01 [Ω]
R
P
(b) ¿Cuál es la resistencia interna de la batería?
La fem está dada por
ε = IR + Ir
= V + Ir
=V +
de manera que
r=
2.3.2.
P
r
V
(ε − V )V
= 5, 76 [Ω]
P
Resistores en serie y en paralelo
En una conexión en serie, si una carga Q sale de un resistor R1 , deberá también
entrar en el segundo resistor R2 . De otra forma, la carga se acumularía en el alambre
2.3. Circuitos
126
entre los resistores. Por lo tanto, en un intervalo dado, la misma carga pasa a través de
ambos resistores
Figura 2.14: conexión de dos resistencias en serie.
En una combinación en serie de dos resistores, las corrientes son las mismas en
ambos resistores, ya que la cantidad de carga que pasa a través de R1 , también pasa a
través de R2 en el mismo intervalo de tiempo
∆V = IR1 + IR2 = I(R1 + R2 ) = IReq .
(2.42)
La resistencia equivalente de tres o más resistores conectados en serie es
Req = R1 + R2 + R3 + . . .
(2.43)
La resistencia equivalente de una conexión en serie de resistores es la suma
algebraica numérica de las resistencias individuales, y es siempre mayor a cualquier
resistencia individual.
Importante: Si una parte de la serie crea un circuito abierto, la serie completa dejará
de funcionar.
Consideremos ahora dos resistores conectados en paralelo. Cuando las cargas llegan
al punto a (unión), éstas se dividen en dos; una parte pasa a través de R1 y el resto a
través de R2 . De esta manera tenemos menos corriente en cada resistor individual que
la que sale de la batería.
2.3. Circuitos
127
Figura 2.15: conexión de dos resistencias en paralelo.
Por otro lado, como ambos resistores están conectados a los terminales de la batería,
la diferencia de potencial aplicada a los resistores es la misma
∆V
∆V
+
= ∆V
I = I1 + I2 =
R1
R2
1
1
+
R1 R2
=
∆V
.
Req
(2.44)
La aplicación de este análisis a tres o más resistores nos da:
1
1
1
1
=
+
+
+ ....
Req
R1 R2 R3
(2.45)
El inverso de la resistencia equivalente de dos o más resistores conectados en paralelo
es igual a la suma de los inversos de las resistencias individuales. Además, la resistencia
equivalente es siempre menor que la resistencia más pequeña en el grupo.
Los circuitos domésticos siempre están alambrados de manera que los aparatos
queden conectados en paralelo. Cada aparato opera independientemente de los demás,
de manera que si un interruptor se abre, los demás permanecerán cerrados. Finalmente,
todos los aparatos funcionan al mismo voltaje.
2.3.2.1.
Ejemplo
Considere la combinación de resistores de la figura (2.16).
2.3. Circuitos
128
Figura 2.16: Circuito formado por resistencias de diferentes valores.
(a) Determine la resistencia entre los puntos a y b.
Req = 9, 11 [Ω]
(b) Si la intensidad de corriente en el resistor de 5 [Ω] es de 1 [A], .cual es la diferencia
de potencial entre los puntos a y b?.
Vab = 97, 2 [Ω]
2.3.2.2.
Ejemplo
Imagine cinco resistores conectados como se muestra en la figura. Determine la
resistencia equivalente entre los puntos a y b.
Figura 2.17
Solución
Debido a la simetría del circuito, las corrientes en las ramas ac y ad deben ser
iguales; en consecuencia, también deben ser iguales los potenciales en los puntos c y d.
2.3. Circuitos
129
Esto significa que ∆Vcd = 0 y que no existe ninguna corriente entre los puntos c y d.
Como resultado, los puntos c y d pueden conectarse entre sí sin afectar al circuito. De
este modo Req = 1 [Ω]
2.3.3.
Leyes de Kirchhoff
Los circuitos sencillos pueden analizarse utilizando la expresión ∆V = IR y las leyes
para las combinaciones en serie y paralelo de los resistores. Para analizar circuitos más
complejos utilizaremos las leyes de Kirchhoff.
Ley de las uniones
La suma de las corrientes que entran a cualquier unión debe ser igual a la de las
corrientes que salen de ella.
X
Ientrada =
X
Isalida .
(2.46)
La primera ley de Kirchhoff es un enunciado de la conservación de la carga eléctrica.
Todas las cargas que entran en un punto dado deben abandonarlo debido a que la carga
no puede acumularse en ese punto.
Figura 2.18: Regla del nodo (unión) de Kirchhoff.
Esto es análogo a una manguera con agua que encuentra una bifurcación. El agua
no puede acumularse en la manguera.
Ley de las mallas
La suma de las diferencias de potencial aplicadas a todos los elementos alrededor de un
circuito cerrado debe ser igual a cero:
X
∆V = 0
circuito
cerrado
(2.47)
2.3. Circuitos
130
La segunda ley de Kirchhoff es una consecuencia de la ley de conservación de la energía.
Imaginemos que movemos una carga alrededor de un circuito cerrado. Cuando la carga
regresa al punto de partida, el sistema carga-circuito debe tener la misma energía total
que la que tenía antes de mover la carga.
La energía potencial se reduce donde la carga pasa a través de una caída de tensión
−IR en una resistencia o donde sea que se mueva en dirección contraria a través de una
fuente fem. La energía potencial aumenta donde la carga pasa a través de la terminal
negativa a la positiva de una batería
Figura 2.19: Reglas para determinar los cambios de potencial a través
de una resistencia y una batería.
En general, para resolver un problema de circuito en particular, el número
de ecuaciones independientes que se necesitan es igual al número de corrientes
desconocidas.
Importante: Cualquier capacitor (condensador) en un circuito funciona como una rama
abierta; es decir, la corriente en la rama que contiene al capacitor es igual a cero bajo
condiciones de estado estable.
2.3.3.1.
Ejemplo
Un circuito de una sola malla contiene dos resistores y dos baterías.
2.3. Circuitos
131
Figura 2.20: Circuito en serie, donde las polaridades de las baterías
están opuestas una de la otra.
(a) Determine la corriente en el circuito.
P
De la malla tenemos que
∆V = ε1 − IR1 − ε2 − IR2 = 0, de modo que I = −0, 33 [A].
El signo negativo de I indica que la dirección de la corriente es la opuesta a la
dirección supuesta.
(b) ¿Qué potencia se entrega a cada resistor?.
La ecuación de potencia es P = IV = I 2 R, de modo que P1 = I 2 R1 = 0, 87 [W ] y
P2 = I 2 R2 = 1, 1 [W ].
(c) ¿Cuál es la potencia entregada por la batería de 12 [V ]?.
La batería de 12 [V ] entrega una potencia de Pb = Iε2 = 3, 96 [W ]. La mitad de esta
potencia es entregada a los dos resistores, mientras que la otra mitad es entregada
a la batería de 6 [V ], la cual está siendo cargada por la batería de 12 [V ].
(d) ¿Qué pasaría si la polaridad de la batería de 12 [V ] se invierte?.
P
De la malla tenemos que
∆V = ε1 − IR1 + ε2 − IR2 = 0, de modo que I = 1, 0 [A].
La corriente sería mayor e iría en la dirección contraria.
2.3.3.2.
Ejemplo
Determine la diferencia de potencial entre los puntos a y b en el circuito de la figura,
y las corrientes I1 , I2 e I3 .
2.3. Circuitos
132
Figura 2.21
Solución
De la unión c se tiene que I2 = I1 + I3 .
P
De la malla de la izquierda tenemos que
∆V = 9[V ] − (9[Ω])I1 − (1[Ω])I2 = 0.
Y de la malla de la derecha tenemos que V = 9[V ] − (9[Ω])I1 − (1[Ω])I2 = 0.
Entonces tenemos tres ecuaciones para tres incógnitas, de modo que las corrientes serán:
19
[A] = 0, 655 [A]
29
I2 = I1 + I3 = 3, 1 [A]
I1 =
como
I2 = 9 − 10I1 : [A] = 2, 45 [A]
Finalmente la diferencia de potencial entre el punto a y b será:
Vab = −(9[Ω])I1 − 8 [V ] = −13, 895 [V ]
2.3.4.
Carga de un condensador
Se le llama circuito RC a un circuito que contiene una combinación en serie de un
resistor y un capacitor. La figura muestra un circuito RC en serie. Supongamos que el
capacitor de este circuito está inicialmente descargado. No existirá corriente mientras el
interruptor esté abierto
2.3. Circuitos
133
(a) Circuito descargado, t < 0.
(b) Circuito cargándose, t > 0.
Figura 2.22: Circuito para la carga de un condensador, antes y después
de cerrar un interrupor.
Si el interruptor se cierra en t = 0 [s], la carga comenzará a fluir, estableciendo una
corriente en el circuito, y el capacitor comenzará a cargarse. Conforme las placas se
cargan, la diferencia de potencial aplicada al capacitor aumenta. Una vez que se alcanza
la carga máxima, la corriente en el circuito es igual a cero, ya que la diferencia de
potencial aplicada al capacitor es igual a la suministrada por la batería. Aplicando la ley
de Kirchhoff tendremos
q(t)
− I(t)R = 0
(2.48)
ε−
c
En el instante en que se cierra el interruptor (t = 0 [s]), la carga del capacitor es igual a
cero.
ε
(corriente en t = 0)
(2.49)
I(t = 0) ≡ I0 =
R
En este caso, la diferencia de potencial aparece aplicada por completo al resistor. Cuando
el capacitor ha sido cargado a su valor máximo Q, las cargas dejan de fluir, la corriente
en el circuito es igual a cero, y la diferencia de potencial de la batería aparece aplicada
al capacitor.
si I = 0 ⇒ Q = C ε
Ahora, recordando que I(t) =
ε−
(carga máxima)
(2.50)
dq(t)
, tenemos
dt
q(t)
dq(t)
−R
=0
C
dt
dq(t)
ε
q(t)
εC − q(t)
⇒
= −
=
dt
R
C
RC
(2.51)
(2.52)
2.3. Circuitos
134
Para encontrar una expresión para q(t), resolvemos esta ecuación diferencial separable,
q(t)
Z
0
εC − q(t)
dq(t)
=
dt
RC
dq(t)
dt
=−
q(t) − εC
RC
Z t
dq(t)
1
=−
dt
q(t) − εC
RC 0
(2.53)
(2.54)
(2.55)
Realizando el cambio de variable u = q(t) − εC tenemos
Z
q(t)−εC
−sC
ln
du
= ln
u
q(t) − εC
−εC
q(t) − εC
−εC
t
=−
RC
=−
t
RC
(2.56)
·e
⇒ q(t) = εC (1 − et/RC )
q(t) = Q(1 − et/RC )
(2.57)
(2.58)
(2.59)
Esta es la carga de un condensador cargándose. De la misma forma tendremos la corriente
de carga,
dq(t)
ε
I(t) =
= exp−t/RC
(2.60)
dt
C
(a) Carga en función del tiempo.
(b) Corriente en función del tiempo.
Figura 2.23: Gráficas de carga y corriente para un circuito RC.
2.3. Circuitos
2.3.4.1.
135
Ejemplo
Considere un circuito RC con un capacitor de capacitancia C descargado, un resistor
de resistencia R, una batería cuya fem es ε y un interruptor. En el instante t = 0 el
interruptor se cierra.
(a) ¿Cuánto tiempo le tomará al capacitor llegar a la mitad de su carga final?.
Q
Q
q(t) = εC (1 − et/RC ) = (1 − et/RC ) =
C
2
1
⇒ t = −RC ln
= 0, 693RC
2
(b) ¿Cuánto tiempo le tomará al capacitor llegar a su carga total?.
Como (t) = Q(1 − expt/RC ), la carga total se alcanzará cuando expt/RC = 0. Como este
término nunca es cero, la carga máxima se logra en t → ∞
(c) Exprese el voltaje en función del tiempo.
V (t) =
2.3.5.
Q
q(t)
= (1 − et/RC ) = ε(1 − et/RC )
C
C
Descarga de un capacitor
Consideremos un circuito formado por un capacitor de carga inicial Q, un resistor y
un interruptor
(a) Circuito cargado, t < 0.
(b) Circuito dencargandose, t >
0.
Figura 2.24: Circuito para la descarga de un condensador.
2.3. Circuitos
136
Cuando el interruptor está abierto, existe una diferencia de potencial Q/C aplicada
al capacitor y una diferencia de potencial igual a cero aplicada al resistor, ya que I = 0.
Si el interruptor se cierra en t = 0, el capacitor comienza a descargarse a través del
resistor
q(t)
− I(t)R = 0
C
q(t)
dq(t)
−
−R
=0
C
dt
Z t
Z q(t)
dq(t)
1
dt
=−
q(t)
RC 0
Q
−
q(t) = Qe−t/RC .
(2.61)
(2.62)
(2.63)
(2.64)
Diferenciando la expresión con respecto al tiempo, obtenemos la corriente instantánea
en función del tiempo
q(t) = Qe−t/RC / dt
dq(t)
Q −t/RC
= I(t) = −
e
= −I0 e−t/RC .
q(t)
RC
2.3.5.1.
(2.65)
(2.66)
Ejemplo
Un capacitor de 3 [µF ] con una carga inicial de 63 [µC ] se descarga a través de un
resistor de 25 [kΩ].
(a) Calcule la intensidad de corriente en el resistor 8 [ms] después de que el resistor se
conecta a través de las terminales del capacitor.
Q −t/RC
e
⇒ I(8 [ms]) = 755, 01 [µA]
RC
(b) ¿Qué carga queda en el capacitor después de 6 [ms]?.
q(t) = Qe−t/RC ⇒ I(6 [ms]) = 2, 77 [µC ]
(c) ¿Cuál es la máxima intensidad de corriente que circula en el resistor?.
Imax =
R
= 840 [µA]
RC
2.3. Circuitos
2.3.5.2.
137
Ejemplo
El circuito mostrado en la figura se ha conectado hace mucho tiempo.
Figura 2.25
(a) ¿Cuál es el voltaje a través del capacitor?. Como ha pasado mucho tiempo, el capacitor
se considerará completamente carga
R5 = 2 [Ω] + 6 [Ω] = 8 [Ω]
R6 = 4 [Ω] + 5 [Ω] = 9 [Ω]
Como los resistores R5 y R6 están conectados en paralelo, la diferencia de potencial a
través de ellos es igual a la diferencia de potencial entre los terminales de la batería.
9
V
= [A]
R5
9
V
I2 =
= 1 [A]
R6
I1 =
La diferencia de potencial a través de las placas del capacitor es
Vab = Vb − Va = (3 [Ω])I1 − (3 [Ω]I2 = 1, 75[V ]
(b) Si la batería se desconectara, ¿cuánto tiempo le toma al capacitor descargarse hasta
1/10 de su voltaje inicial?.
Si la batería se desconecta entonces:
R5 = 2 [Ω] + 4 [Ω] = 6 [Ω]
R6 = 6 [Ω] + 5 [Ω] = 11 [Ω]
2.3. Circuitos
138
Como los resistores R5 y R6 están conectados en paralelo, entonces la resistencia
equivalente seria Req = 3, 88 [Ω]. Luego tendremos que:
q(t)
Q
V0
= e−t/RC =
C
C
10
⇒ t = RC ln 10 = 26, 2 [µs]
V (t) =
2.3.6.
Medidores eléctricos
El amperímetro
es un aparato que mide la corriente. Cuando se utiliza un amperímetro para medir
corrientes directas, debe conectarse de tal manera que las cargas entren al instrumento
por la terminal positiva y salgan por la negativa. Idealmente, un amperímetro debe tener
una resistencia cero para que la corriente a medir no se vea alterada
Figura 2.26: Amperímetro conectado en serie que permite medir la
corriente.
El voltímetro
es un aparato que mide la diferencia de potencial. La diferencia de potencial aplicada
al resistor R2 se mide al conectar el voltímetro en paralelo con R2 . La terminal positiva
del voltímetro debe estar conectada al extremo del resistor que tenga el potencial más
alto. Un voltímetro ideal tiene una resistencia infinita que impide que la corriente pase
a través de él
2.3. Circuitos
Figura 2.27: Voltímetro conectado en paralelo que permite medir la
diferencia de potencial.
139
140
2.3. Circuitos
Ejercicios Propuestos
Transporte eléctrico.
1. La cantidad de carga q que pasa a través de una superficie de área 1 [mm2 ] varía con
el tiempo de acuerdo con la expresión q(t) = 4t 3 − 6t 2 + 6.
(a) ¿Cuál es la intensidad de corriente instantánea a través de la superficie en t = 2[s]?.
(b) ¿Cuál es el valor de la densidad de corriente en t = 2 [s]?.
(c) ¿En qué instante alcanza la mínima intensidad de corriente instantánea?.
2. Suponga que la corriente que circula a través de un conductor decrece exponencialmente con el tiempo de acuerdo con la expresión I(t) = I0 exp −t/τ, donde I0 es la
intensidad de corriente inicial (en t = 0 [s]) y τ es una constante que tiene dimensiones de tiempo. Considere que se realiza una observación en un punto interno del
mismo conductor.
(a) ¿Cuánta carga pasa por ese punto entre t = 0 y t = τ?.
(b) ¿Cuánta carga pasa por ese punto entre t = 0 y t = 10τ?.
(c) ¿Cuánta carga pasa por ese punto entre t = 0 y t = ∞?.
3. Por un alambre de cobre de 2, 54 [mm] de diámetro circula una corriente de 0, 5 [A].
Calcule la velocidad media de los electrones. Suponga que la concentración de
electrones libres es 8 × 1028 [electrones/m3 ].
142
Ejercicios propuestos transporte eléctrico.
4. Considere un conductor de forma de cónico circular truncado, como se ilustra en la
figura 5.17. El radio de la sección S1 es 0,5 (cm), si la intensidad de corriente en el
conductor es de 8 (A).
(a) ¿Cuál es la densidad de corriente en S1 ?.
(b) Si la densidad de corriente en S2 es la cuarta parte del valor en S1 , ¿cuál es el
radio del conductor en S2 ?.
Figura 2.28: (Problema 4).
5. Por un alambre de radio uniforme de 0, 26 [cm] fluye una corriente de 10 [A] producida
por un campo eléctrico de magnitud 110 [V /m]. ¿Cuál es la resistividad del material?.
6. 25 alambres de cobre de la misma longitud l y diámetro d, se unen en paralelo para
formar un cable de resistencia R. ¿Cuál debe ser el diámetro D de un sólo alambre de
cobre de la misma longitud l para que tenga la misma resistencia?.
7. Se fabrican dos conductores de cobre con la misma longitud. El conductor A es un
alambre sólido de 1[mm] de radio. El conductor B es un tubo cilíndrico de radio interno
1 [mm] y radio externo 2 [mm]. ¿Cuál es la relación RA /RB entre las resistencias?.
8. Un alambre tiene forma de cono circular truncado, como se muestra en la figura 3.23.
Los radios de los extremos son r1 y r2 y altura L. Si la abertura es pequeña, encontrar
una expresión para la resistencia entre los extremos del alambre.
Ejercicios propuestos transporte eléctrico.
143
Figura 2.29: (Problema 8).
9. A un alambre de resistencia 10 [Ω] de forma cilíndrica con longitud 25 [mm] y diámetro
0, 4 [cm], se le aplica una diferencia de potencial de 1 [V ].
(a) Calcule la intensidad de corriente en el alambre.
(b) Calcule el campo eléctrico en el conductor.
(c) Calcule la densidad de corriente.
10. ¿A qué temperatura se triplica la resistividad del platino con respecto a su valor medido
a −10◦ C ?. (Utilice α = 3, 92 × 10−3 1/ ◦ C ).
11. Calcule el porcentaje de cambio en la resistencia de un filamento de oro cuando es
calentado desde la temperatura ambiente hasta 200 ◦ C . (Utilice α = 3, 4 × 10−3 [1/ ◦ C ]).
12. Una lámpara eléctrica de 10 [Ω] se etiqueta a 100 [W ] (máxima potencia permitida).
¿Cuál es el máximo voltaje de operación que soportaría?.
13. Dos conductores del mismo material están conectados a través de una diferencia de
potencial común. El conductor A tiene el triple de diámetro y la tercera parte de la
longitud que el conductor B. ¿Cuál es la razón de las potencias entregadas por los dos
conductores?.
14. La resistividad del tungsteno aproximadamente aumenta linealmente desde 56 [nΩm]
a 293 [K ] hasta 1, 1 [nΩm] a 3500 [K ]. Estime:
Ejercicios propuestos transporte eléctrico.
144
(a) La resistencia.
(b) El diámetro de un filamento de tungsteno usado en una ampolleta de 40 [W ],
asumiendo que la temperatura del filamento es 2500[K ], y que hemos usado 100[V ]
para encender la ampolleta. Asuma que la longitud del filamento es constante e
igual a 0, 5 [cm].
15. Una batería tiene una fem de 30[V ]. El voltaje en las terminales de la batería disminuye
a 24 [V ] cuando se disipan 25 [W ] de potencia en un resistor externo R.
(a) ¿Cuál es el valor de R?.
(b) ¿Cuál es la resistencia interna de la batería?.
16. Dos resistores de resistencia R1 y R2 (R1 < R2 ) se conectan en paralelo y después en
serie a una batería de voltaje V . En el circuito en serie y en paralelo:
(a) ¿Cuál resistor disipa más potencia?.
(b) Verifique que la suma de las potencias disipadas en los resistores es igual a la
potencia suministrada por la batería.
17. Considere la combinación de resistores en la figura 2.30.
(a) Determine la resistencia equivalente entre los puntos a y b.
(b) Si la intensidad de corriente en el resistor de 5 [Ω] es de 1 [A], ¿cuál es la diferencia
de potencial entre los puntos a y b?.
Figura 2.30: (Problema 17).
Ejercicios propuestos transporte eléctrico.
145
18. Tres resistores de 10 [Ω] cada uno pueden disipar una potencia máxima de 2, 5 [W ], y
se conectan como muestra en la figura 2.31.
(a) ¿Cuál es el máximo voltaje que se puede aplicar en las terminales a y b?.
(b) Para el voltaje determinado en la pregunta (a), ¿cuál es la potencia disipada en
cada resistor?.
(c) ¿Cuál es la potencia total disipada en el circuito?.
Figura 2.31: (Problema 18).
19. Determine la diferencia de potencial entre los puntos a y b, y las corriente I1 , I2 , y I3 ,
en el circuito de la figura 2.32.
Figura 2.32: (Problema 19).
20. Determine la diferencia de potencial Vab para el circuito de la figura 2.33.
Ejercicios propuestos transporte eléctrico.
146
Figura 2.33: (Problema 20).
21. Considerando el circuito de la figura 2.34,
(a) Calcule el valor del resistor R.
(b) Determine la intensidad de corriente que fluye en los resistores de 3 [Ω] y 2 [Ω].
Figura 2.34: (Problema 21).
22. Considerando el circuito de la figura 2.35,
(a) Determine el valor de la intensidad de corriente en cada rama.
(b) Encuentre la carga en los condensadores (considerando que están completamente
cargados).
Ejercicios propuestos transporte eléctrico.
147
Figura 2.35: (Problema 22).
23. Considere un circuito RC , con un capacitor de capacitancia C descargado, un resistor
de resistencia R, una batería cuya fem es ε y un interruptor, como se muestra la figura
2.36. En el instante t = 0 [s] el interruptor se cierra.
(a) ¿Cuánto tiempo le tomará al capacitor llegar a la mitad de su carga final?.
(b) ¿Cuánto tiempo le tomara al capacitor llagar a su carga total?.
Figura 2.36: (Problema 23).
24. El circuito de la figura 2.37 se ha conectado hace mucho tiempo.
(a) ¿Cuál es el voltaje a través del capacitor?.
(b) Si la batería se desconectara, ¿cuánto tiempo le tomaría al capacitor descargarse
hasta 1/10 de su voltaje inicial?.
148
Ejercicios propuestos transporte eléctrico.
Figura 2.37: (Problema 24).
25. Considere un capacitor de 6 [µF ] cargado a un voltaje de 100 [V ] y luego conectado a
través de una resistencia de 500 [Ω].
(a) ¿Cuál es la carga inicial sobre el condensador?.
(b) ¿Cuál es la corriente inicial en el instante inmediatamente después de que el condensador es conectado a la resistencia?.
(c) ¿Cuál es la constante de tiempo del circuito?.
(d) ¿Cuál es la carga en el condensador después de 6 [ms]?.
(e) Encuentre la energía inicial almacenada en el condensador.
(f) Demuestre que la energía almacenada en el condensador está dada por U =
U0 e−2t/τ , donde U0 es la energía inicial y τ = RC es la constante de tiempo.
(g) Grafique esquemáticamente la energía U en el condensador versus el tiempo t.
Capítulo 3
Magnetismo
e estima que la Tierra ha sufrido más de veinte inversiones, la más reciente sucedió
hace 700.000 años. Otras inversiones ocurrieron hace 870.000 y 950.000 años. El
problema es que el fenómeno no sigue ningún ciclo definido aunque casi todos los estudios
se basan en el ritmo de reducción de la intensidad del campo magnético. Otros estudios se
basan en pautas migratorias de la golondrina angoleña. Una inversión podría significar
serios desajustes a nivel tecnológico (satélites, comunicaciones, . . .) y podría provocar
efectos sobre el clima (tornados y tormentas tropicales). Algunos teóricos especulan sobre
que también provoque movimientos tectónicos. Además, la atracción sobre los cuerpos
celestes se vería afectada.
S
3.1.
Campo de inducción magnético
3.1.1.
Historia
XIII a.c. Se inventa la brújula (origen árabe e hindú), la que utiliza una aguja
magnética, y es utilizada por los chinos.
800 a.c. Los griegos descubrieron que la magnetita (Fe3 O4 ) atrae fragmentos de
hierro. La leyenda adjudica el nombre magnetita al pastor Magnes, que atraía trozos de
magnetita mientras pastoreaba sus rebaños con los clavos de sus sandalias.
1269 Pierre de Maricourt descubrió que las direcciones en las que apuntaba una
aguja al acercársele un imán esférico natural formaban líneas que rodeaban a la esfera
3.1. Campo de inducción magnético
150
y pasaban a través de los polos de imán.
Polos iguales se repelen.
Polos opuestos se atraen.
Los polos son llamados así (Norte y Sur) por la forma en que un imán se comporta
en presencia del campo magnético de la Tierra. El polo Norte del imán apunta
aproximadamente hacia el polo Norte geográfico de la Tierra.
1600 William Gilbert amplió el experimento de Maricourt aplicándolo a una diversidad
de materiales. Sugirió que la Tierra es un imán permanente gigantesco.
1750 Utilizando balanzas de torsión se demostró que los polos magnéticos ejercen
entre sí fuerzas de atracción y repulsión, y que varían con el inverso del cuadrado de sus
distancias.
Las cargas eléctricas pueden aislarse (electrón y protón), en tanto que nunca ha sido
posible aislar un sólo polo magnético. Los polos magnéticos siempre se encuentran en
pares.
1819 Hans Oersted descubrió que la aguja de la brújula se desvía si se coloca cerca
de un circuito por el que pasa una corriente eléctrica. Así nació el electromagnetismo.
1831 Michael Faraday y Joseph Henry demostraron que cuando un imán se mueve
cerca de un alambre, se establece una corriente eléctrica en dicho alambre. Este efecto
se conoce como inducción electromagnética. Además Fadaray introdujo el concepto de
campo eléctrico.
1873 James Clerck Maxwell aprovechó estas observaciones junto con otros experimentos como base para formular las leyes fundamentales del electromagnetismo.
1888 Heinrich Hertz comprobó las predicciones de Maxwell al producir ondas
electromagnéticas en su laboratorio. Este logro hizo posible desarrollos prácticos como
la radio y la television.
3.1. Campo de inducción magnético
3.1.2.
151
Campos y fuerzas magnéticas
Recuerde que cualquier carga eléctrica esta rodeada por un campo eléctrico. Además
de contener un campo eléctrico, el espacio que rodea a cualquier carga eléctrica en
movimiento contiene un campo magnético. La dirección del campo magnético en cualquier
sitio es la dirección a la cual apunta la aguja de una brújula en dicha posición. Es posible
representar el campo magnético utilizando líneas de campo magnético
Figura 3.1: Líneas de campo magnético, dentro y fuera de una barra
magnética.
~ en algún punto en el espacio como función de
Podemos definir un campo magnético B
la fuerza magnética F~B que ejerce el campo sobre una partícula cargada que se mueve
con una velocidad ν~ . Por ahora vamos a suponer que no existen ni campo eléctrico ni
campo gravitacional.
La magnitud FB de la fuerza magnética ejercida sobre la partícula es proporcional
a la carga q y a la velocidad ν de dicha partícula.
La magnitud y dirección de F~B dependen de la velocidad de la partícula y de la
magnitud y dirección del campo magnético.
Cuando una partícula cargada se mueve en forma paralela al vector del campo
magnético, la fuerza magnética que actúa sobre ella es cero.
3.1. Campo de inducción magnético
152
Cuando el vector de velocidad de la partícula forma un ángulo θ 6= 0 con el campo
magnético, la fuerza magnética actúa en dirección perpendicular tanto a como a ν~
~
como a B.
La fuerza magnética ejercida sobre una carga positiva tiene dirección opuesta a la
ejercida sobre una carga negativa que se mueve en la misma dirección.
La magnitud de la fuerza magnética que se ejerce sobre una partícula en movimiento
~
es proporcional a sin θ, siendo θ el ángulo de la velocidad con B
~
F~B = q~
ν x B.
(3.1)
Figura 3.2: Dirección y sentido de la fuerza magnética sobre una
partícula cargada.
La magnitud de la fuerza magnética sobre una partícula cargada es
F~B = |q|νB sin θ,
(3.2)
~
donde θ es el ángulo menor entre ν~ y B.
3.1.3.
Diferencias entre fuerza eléctrica y magnética
La fuerza eléctrica actúa a lo largo de la dirección del campo eléctrico, mientras
que la fuerza magnética actúa perpendicularmente a éste.
3.1. Campo de inducción magnético
153
La fuerza eléctrica actúa sobre una partícula cargada sin importar si ésta se
encuentra en movimiento, mientras que la fuerza magnética actúa sólo cuando la
partícula está en movimiento.
La fuerza eléctrica realiza trabajo al desplazar una partícula cargada, en tanto que
la fuerza magnética no efectúa trabajo cuando se desplaza una partícula, debido a
que la fuerza es perpendicular al desplazamiento.
Como F~B = |q|νB sin θ entonces el campo magnético se mide en
1 T (Tesla) = 1
Ns
N
=
= 104 G (Gauss).
C · m/s
Cm
Fuente
Campo [T]
Imán Superconductor
30
Imán Laboratorio
2
Imán Barra
Superficie Tierra
Impulsos Nerviosos del Cerebro
(3.3)
10−2
0, 5 · 10−4
10−13
Cuadro 3.1: Valores de campo magnético de distintos materiales
3.1.3.1.
Ejemplo
Una partícula alfa tiene una velocidad de ν~ = (3ı̂ + 5̂ − 9k̂) [m/s] dentro de un campo
~ = (3ı̂ − 20̂ + 5k̂) [µT ]. ¿Cuál es la fuerza que siente la
magnético uniforme dado por B
partícula alfa?.
~ = (−4, 96ı̂ − 1, 34̂ − 2, 4k̂) · 1023 ‘[N]
F~B = q~
ν×B
3.1.4.
(3.4)
Movimiento de una partícula cargada en un campo magnético uniforme
La fuerza magnética que actúa sobre una partícula cargada que se mueve en un
campo magnético es perpendicular a la velocidad de la partícula, y por lo tanto, el trabajo
realizado por la fuerza magnética sobre la partícula es igual a cero.
3.1. Campo de inducción magnético
154
Conforme la partícula cambia la dirección de su velocidad como respuesta a la fuerza
magnética, ésta se mantiene en posición perpendicular a la velocidad. Si la fuerza es
siempre perpendicular a la velocidad, la trayectoria de la partícula es un círculo.
Figura 3.3: Partícula cargada que se mueve perpendicular a un campo
magnético uniforme
X
F = mac
mν 2
r
mν
⇒ r=
.
qB
FB = qνB =
(3.5)
(3.6)
(3.7)
El radio de la trayectoria es proporcional a la cantidad de movimiento lineal mν de la
partícula e inversamente proporcional a la magnitud de carga y del campo magnético.
La velocidad angular de la partícula es
ω=
ν
qB
=
r
m
(frecuencia de ciclotrón).
(3.8)
El periodo del movimiento (tiempo para completar una vuelta) es
T =
2πr
2π
2πm
=
=
.
ν
ω
qB
(3.9)
3.1. Campo de inducción magnético
155
Si una partícula cargada se mueve en un campo magnético uniforme con su velocidad
~ su trayectoria será una
orientada para formar algún ángulo arbitrario con respecto B,
hélice.
Figura 3.4: Partícula cargada, que posee una componente de velocidad
paralelo a un campo magnético y otro perpendicular al mismo.
Si el campo está dirigido a lo largo del eje de las x, no existirá componente de la
fuerza en esta dirección. Como resultado, la aceleración a lo largo de esta dirección será
cero y, por lo tanto, νx se mantendrá constante.
3.1.4.1.
Ejemplo
Un protón cuya energía es de 750 [eV ] está circulando en un plano formando un
ángulo recto con un campo magnético uniforme. El radio de la trayectoria circular es
0, 8 [m]. Calcule la magnitud del campo magnético.
Solución
K = (750 [eV ])(1, 6 · 10−19 [J/eV ]) = 1, 2 · 10−16 [J]
mν
mν
⇒ B=
qB
qr
r
1 2
2K
mientras que la energía cinética de la partícula es K = mν ⇒ ν =
2
m √
r
mν
m 2K
2mK
De esta forma, el campo magnético quedará como B =
=
=
=
qB
qr
m
qr
4, 95[mT ]
El radio de curvatura de la trayectoria es r =
3.1. Campo de inducción magnético
156
3.1.4.2.
Ejemplo
Un ión con carga +2e tiene una masa de 3, 2 · 10−26 [kg]. Se acelera desde el reposo
por una diferencia de potencial de 900 [V ] y luego entra en un campo magnético uniforme
de 0,98 [T ], perpendicularmente.
(a) Calcule la velocidad del ión.
El trabajo que realiza el campo eléctrico en la región donde existe la diferencia de
potencial sobre la carga está dado por W = q∆V . Por otro lado, el trabajo es igual a
la diferencia de energía cinética, y como la partícula inicialmente estaba en reposo,
1
entonces W = q∆V = mν 2
2
r
ν=
hmi
2q∆V
= 1, 34 · 105
m
s
(b) Calcule el radio de su trayectoria dentro del campo magnético.
m
m
r=
ν=
qB
qB
3.1.5.
s
r
1
2q∆V
=
m
B
2q∆V
= 13, 69 [mm]
q
Fuerza magnética que actúa sobre un conductor que transporta
corriente
Si se ejerce una fuerza sobre una partícula cargada cuando ésta se mueve a través
de un campo magnético, es lógico pensar que un alambre que transporta una corriente
también experimente una fuerza cuando se le coloca en un campo magnético.
La corriente es un conjunto de muchas partículas cargadas en movimiento.
La fuerza resultante ejercida por el campo sobre el alambre es la suma vectorial
de las fuerzas individuales ejercidas sobre todas las partículas cargadas.
3.1. Campo de inducción magnético
157
Figura 3.5: Alambre vertical flexible sobre un campo. Cuando no existe
corriente en el alambre éste permanece vertical, pero cuando circula
corriente este de desvía hacia la izquierda o derecha según el sentido
de la corriente.
Consideremos un segmento recto de alambre de longitud L y sección transversal A,
~ La fuerza magnética que
que lleva una corriente I en un campo magnético uniforme B.
se ejerce sobre una carga q en movimiento, con una velocidad media ν~m , es
~
F~B = q~
νm × B.
(3.10)
Para encontrar la fuerza total que actúa sobre el alambre, multiplicamos la fuerza
ejercida sobre una carga por el número de cargas en el segmento que es nAL, donde n es
el número de cargas por unidad de volumen. La fuerza magnética total sobre el alambre
es entonces
~
F~B = (q~
νm × B)nAL,
(3.11)
y como la corriente en el alambre es I = nqνm A, entonces
~
F~B = I L~ × B,
(3.12)
donde L~ es un vector que apunta en la dirección de la corriente I y que tiene una magnitud
igual a la longitud L del segmento de alambre.
Consideremos ahora un segmento de alambre de forma arbitraria con sección
transversal uniforme en un campo magnético.
3.1. Campo de inducción magnético
158
Figura 3.6: Alambre que lleva una corriente I en un campo magnético
externo B.
La fuerza magnética que se ejerce sobre una longitud d~l de un pequeño segmento de
~ es
vector en presencia de un campo B
~
dF~B = IdL~ × B.
(3.13)
Para calcular la fuerza total dF~B que actúa sobre el alambre, integramos en la longitud
total del alambre
F~B = I
Z
b
a
~
dL~ × B.
(3.14)
Vamos a suponer ahora dos casos, donde el campo magnético es uniforme en magnitud
y dirección:
1. Un alambre curvo transporta una corriente I y está localizado en un campo
~
magnético uniforme B
3.1. Campo de inducción magnético
159
Figura 3.7: Conductor curvo.
Dado que el campo es uniforme, entonces
F~B = I
Z
b
!
dL~
a
~
×B
(3.15)
donde la integral representa la suma vectorial de todos los elementos de longitud
desde a hasta b. Según la Ley de Adición Vectorial, la suma es igual al vector L~0
~
F~B = I L~0 × B
(3.16)
La fuerza magnética ejercida sobre un alambre curvo que transporta corriente es
igual a la ejercida sobre un alambre recto que conecta los puntos extremos y que
conduce la misma corriente.
2. En un campo magnético uniforme se coloca una espira de forma arbitraria que
conduce una corriente I.
3.1. Campo de inducción magnético
160
Figura 3.8: Espira de corriente.
Dado que el campo magnético es uniforme,
F~B = I
I
~
~
dL × B
(3.17)
Como el conjunto de elementos de longitud forma un polígono cerrado, la suma
vectorial es cero.
I
dL~ = 0 ⇒ F~B = 0
(3.18)
La fuerza magnética que actúa sobre cualquier lazo cerrado de corriente en un
campo magnético uniforme es igual a cero.
3.1.5.1.
Ejemplo
Un alambre de 0, 06 [kg/m] está suspendido por un par de puntas flexibles dentro de
un campo magnético de 440 [mT ]. Determine la magnitud y dirección de la corriente en
el alambre para que la tensión en las puntas sea cero
3.1. Campo de inducción magnético
161
Figura 3.9: Alambre suspendido dentro de un campo magnético.
Solución
Del diagrama de cuerpo libre tenemos F~B + F~g = 0 ⇒ F~B = mg
~ = B k̂ es perpendicular al alambre L~ = −lı̂, entonces la
Como el campo magnético B
~ = IlB̂.
fuerza magnética está dada por F~B = I L~ × B
Igualando entonces tendremos que
mg
F~B = IlB = mg ⇒ I =
= 1, 34 [A]
lB
Considerando la dirección de la corriente tendremos que ~I = −1, 34ı̂ [A]
3.1.6.
Ley de Biot-Savart
Jean Baptiste Biot (1774-1862) y Félix Savart (1791-1841) realizaron experimentos
cuantitativos con respecto a la fuerza ejercida por una corriente eléctrica sobre un imán
cercano. Biot y Savart obtuvieron el campo magnético generado por una corriente
3.1. Campo de inducción magnético
162
~ producido por un conductor rectilíneo
Figura 3.10: campo magnético B
indefinido por el que circula una corriente de intensidad I.
~ es perpendicular tanto a d~l como al vector r̂.
El vector dB
~ es inversamente proporcional a r 2 , siendo r la distancia de d~l
La magnitud de dB
a P.
~ es proporcional a la corriente y a la magnitud d~l del elemento
La magnitud de dB
de longitud d~l
~ es proporcional a sin θ donde θ es el ángulo entre los vectores
La magnitud de dB
d~l y r̂.
De esta forma, la Ley de Biot-Savart está dada por
~=
dB
µ0 Id~l × r̂
,
4π r 2
donde µ0 es una constante llamada permeabilidad del espacio libre
Tm
.
µ0 = 4π × 107
A
(3.19)
(3.20)
~ total que se crea en algún punto por una
Para determinar el campo magnético B
corriente de tamaño finito tendremos
Z ~
dl × r̂
~ = µ0 I
B
.
(3.21)
4π
r2
3.1. Campo de inducción magnético
3.1.6.1.
163
Ejemplo
Imagine un alambre recto y delgado que lleva una corriente constante I, colocado a
lo largo del eje x. Determine la magnitud y dirección del campo magnético en el punto
P generado por esta corriente.
Figura 3.11: Segmento de alambre recto que lleva una corriente I.
Solución
Utilizando la ecuación de Biot-Savar (3.19), tenemos
µ0 Id~s × r̂
4π r 2
Para integrar esta expresión debemos desarrollar
~=
dB
d~s × r̂ = |d~s × r̂|k̂ = (dx sin θ)k̂
y relacionar las variables θ, x, r. Un procedimiento es expresar x y r como función de θ.
a
sin θ =
r
a
⇒ r=
sin θ
tan θ =
a
−x
cos θ
sin θ
dθ
⇒ dx = a 2
sin θ
⇒ x = −a
3.1. Campo de inducción magnético
164
De modo que
~=
dB
=
=
~=
B
~=
B
µ0 I dx sin θ
k̂
4π
r2
µ0 I
sin2 θ adθ
k̂
sin θ 2
4π
a sin2 θ
Z
µ0 I
sin θdθ k̂
4π
Z
µ0 I θ2
sin θdθ k̂
4π θ1
µ0 I
(cos θ1 − cos θ2 )k̂
4π
Si realizamos la aproximación de que el alambre es infinitamente largo, entonces θ1 = 0
y θ2 = π. De esta forma
~ = µ0 I (cos 0 − cos π)k̂ = µ0 I k̂.
B
4π
4πa
3.1.6.2.
Ejemplo
Considere una espira de alambre circular de radio R localizada en el plano yz y que
transporta una corriente estable I. Calcule el campo magnético en un punto P en el eje
a una distancia x del centro de la espira.
Figura 3.12: Espira de corriente.[4]
3.1. Campo de inducción magnético
165
Solución
En este caso cada uno de lo elementos de longitud d~s son perpendiculares al vector
r̂ en la localización del elemento
π |d~s × r̂| = ds sin
= ds
2
Además, todos los elementos de longitud alrededor de la espira están a la misma distancia
√
r de P, donde r = x 2 + R 2
~ debido a la corriente en cualquier elemento de
En consecuencia, la magnitud de dB
~ es
longitud dB
ds
~ = µ0 I |d~s × r̂| = µ0 I
dB
2
2
4π
4π (x + R 2 )
r
El campo resultante en P debe estar a lo largo del eje de las x y podemos determinarlo
integrando los componentes
~ x = dB cos θ ⇒ B
~ = Bx ı̂
dB
De esta manera tenemos
I
Bx =
µ0 I
dB cos θ =
4π
I
ds cos θ
.
x2 + R2
Debido a que θ, x, y R son constantes para todos los elementos de la espira, y ya que
R
cos θ = √
, entonces obtendremos que
x2 + R2
I
µ0 IR
µ0 IR 2
Bx =
ds
=
4π(x 2 + R 2 )3/2
2(x 2 + R 2 )3/2
Para determinar el campo magnético en el centro de la espira reemplazaremos x = 0.
Bx =
3.1.7.
µ0 I
2R
(x = 0)
Fuerza magnética entre dos conductores paralelos
Debido a que la corriente en un conductor genera su propio campo magnético, es fácil
entender que dos conductores que transportan una corriente ejercen fuerzas magnéticas
entre sí. Imagínese dos alambres largos, rectos, paralelos, separados por una distancia
a, y que llevan corrientes I1 y I2 en la misma dirección.
3.1. Campo de inducción magnético
166
Figura 3.13: Dos alambres paralelos por los cuales circula una
corriente que ejercen fuerza uno sobre otro.
Podemos determinar la fuerza ejercida sobre un alambre debido al campo magnético
~ 2 en la ubicación
desplegado por el otro alambre. El alambre 2 crea un campo magnético B
del alambre 1.
~
F~B = I L~ × B
(3.22)
~ 2,
F~1 = I1 L~ × B
(3.23)
y puesto que
B2 =
entonces
µ0 I2
,
2πa
F1 = I1 LB2 = I1 L
µ0 I2
2πa
(3.24)
=
µ0 I1 I2
L.
2πa
(3.25)
~ B
~ 2 apunta en esa dirección.
La dirección de F~1 es hacia el alambre 2, debido a que L×
Cuando las corrientes se encuentran en direcciones opuestas, las fuerzas se invierten y
los alambres se repelen.
De esta forma podemos concluir que dos conductores que llevan corrientes en una
misma dirección se atraen, mientras que dos conductores paralelos que llevan corrientes
en direcciones opuestas se repelen
FB
µ0 I1 I2
=
.
L
2πa
(3.26)
3.2. Ley de Ampere
3.2.
167
Ley de Ampere
l descubrimiento de Oersted en 1819 respecto al desvío de la aguja de las brújulas
demuestra que un conductor que lleva una corriente produce un campo magnético.
E
(a) Cuando no existe corriente en el alambre todas (b) Cuando existe corriente en el alambre, las
las brújulas apuntan en la misma dirección
brújulas apuntan de forma tangente a un circulo
~ debido a la
cuya dirección es el campo B
corriente.
Figura 3.14: Experimento realizado por Oersted que demuestra que un
conductor que lleva corriente produce un campo magnético.[4]
Cuando no hay corriente en el alambre, todas las agujas apuntan en una misma
dirección (la del campo magnético de la Tierra). Cuando el alambre lleva una corriente,
fuerte y estable, todas las agujas se desvían en una dirección tangente al círculo.
~ a lo largo de un camino cerrado en presencia de
Veamos la integral curvilínea de B
este campo. Consideremos el camino ABCD
3.2. Ley de Ampere
168
~ a lo largo de un camino cerrado
Figura 3.15: integral curvilínea de B
ABCD.
~ a lo largo del camino representado es nula. Los caminos
La integral curvilínea de B
~ y en nada contribuyen. A lo largo de AB, B
~ es más
BC y DA son perpendiculares a B
intenso que a lo largo de C D en la relación r2 /r1 , pero C D es más largo que AB en la
misma relación, pues estos dos arcos presentan el mismo ángulo en el hilo. Como AB y
C D dan contribuciones iguales y de signo contrario, la integral total es nula.
Se deduce que la integral curvilínea es también nula a lo largo de todo camino que
pueda construirse con segmentos radiales y arcos. Se deduce entonces que la integral
curvilínea es nula a lo largo de todo camino que no encierre el hilo conductor
I
~ · d~l = 0
B
No encierra
Consideremos ahora un camino circular que rodea al conductor
(3.27)
3.2. Ley de Ampere
169
Figura 3.16: Camino circular que rodea un conductor
~ · d~l para un pequeño elemento de longitud d~l de
Ahora evaluaremos el producto B
la trayectoria circular, y sumaremos los productos para todos los elementos alrededor
~ son
de la trayectoria circular cerrada. A lo largo de esta trayectoria, los vectores d~l y B
~ · d~l = Bd~l. Además la magnitud de B
~ es constante y
paralelos en cada punto, así que B
está dada por
~ = µ0 I
(3.28)
|B|
2πr
Por lo tanto, la suma de los productos Bdl a lo largo de la trayectoria cerrada es
I
~ · d~l = B
B
I
dl =
µ0 I
(2πr) = µ0 I
2πr
(3.29)
Pretendemos que todo camino que encierre el hilo tenga el mismo valor. Por ejemplo,
consideremos el camino irregular C de la figura
Figura 3.17: Camino irregular C que rodea un conductor.
3.2. Ley de Ampere
170
Construyamos ahora el camino C 0 formado por un camino como el C y uno circular,
pero que no encierre el hilo
Figura 3.18: Camino irregular C 0 que rodea un conductor.
La integral curvilínea a lo largo de C 0 debe ser nula, por lo que la integral a lo largo
de C debe ser igual a la integral a lo largo de la circunferencia con el signo contrario.
El signo depende del sentido de recorrido del campo.
El caso general, conocido como la Ley de Ampere, puede enunciarse como: la integral
~ · d~l alrededor de cualquier trayectoria cerrada es igual a µ0 I, donde I es la
lineal B
corriente total estable que pasa a través de cualquier superficie limitada por la trayectoria
cerrada.
I
~ · d~l = µ0 I
B
(3.30)
3.2.0.1.
Ejemplo
Un alambre largo y recto de radio R lleva una corriente estable I uniformemente
distribuida a través de la sección transversal del alambre. Calcule el campo magnético a
una distancia r del centro del alambre en las regiones:
(a) r > R
I
~ · d~l = B
B
I
dl = B(2πr) = µ0 I
⇒ B=
µ0 I
2πr
3.2. Ley de Ampere
171
(b) r < R
I0
πr 2
=
I
πR 2
r2
⇒ I0 = 2 I
R
I
I
~ · d~l = B dl = B(2πr) = µ0 I 0
B
reemplazando el valor de I 0 tenemos
r2
µ0 I = µ0
I
R2
2 r
I
⇒ B(2πr) = µ0
R2
µ0 Ir
⇒ B=
2πR 2
0
3.2.0.2.
Ejemplo
El dispositivo llamado toroide es utilizado para crear un campo magnético casi
uniforme en algún área cerrada. Un alambre conductor es enrollado sobre un anillo
hecho de algún material no conductor. Para un alambre de N vueltas de alambre muy
apretado, calcule el campo magnético en la región ocupada por el toro, a una distancia
r de su centro.
Figura 3.19: Bobina toroidal.[4]
3.2. Ley de Ampere
172
Solución
Por simetría vemos que la magnitud del campo es constante en este circuito y es
~ · d~l = Bdl. Además, el alambre pasa por la espira N veces,
tangente a él, por lo que B
de modo que la corriente total a través de la espira es NI.
I
I
~
~
B · dl = B dl = B(2πr) = µ0 NI
µ0 NI
b<r<c
2πr
Si r es muy grande en comparación con la sección transversal del toro, entonces en su
interior el campo es uniforme.
⇒ B=
3.2.1.
Campo magnético debido a un solenoide
Un solenoide es un alambre largo enrollado en forma de hélice. Si las vueltas están
muy apretadas y el solenoide es de longitud finita, las líneas de campo magnético son
Figura 3.20: Líneas de campo magnético para un solenoide de vueltas
estrechas con longitud finita y corriente constante.[4]
I
~ · d~l = BL = µ0 NI
B
(3.31)
N
I = µ0 nI,
L
(3.32)
⇒ B = µ0
3.2. Ley de Ampere
donde n =
N
L
173
es el número de vueltas por unidad de longitud.
Tomemos ahora una curva cerrada C en una región donde circulen corrientes. La
corriente encerrada por C es el flujo de ~J a través de la superficie abarcada por C , es
decir, la integral de superficie
Z
~
I = ~J · dS,
(3.33)
s
de modo que
I
~ · d~l = µ0 I = µ0
B
recordando el teorema de Stokes
I
F~ · d~l =
I
s
Z
~J · dS,
~
s
~
~ × F~ ) · dS,
(∇
(3.34)
(3.35)
Así que
I
~ · d~l =
B
Z
s
~ = µ0
~ × F~ ) · dS
(∇
Z
~J · dS
~
s
~ × F~ = µ0~J.
⇒ ∇
(3.36)
(3.37)
~ dado ~J ya que
Sin embargo, la ecuación anterior no es suficiente para determinar B
distintos vectores campo podrían tener el mismo rotacional. La divergencia del campo
magnético de un solo hilo recto es nula. Esto debido a que no es posible dibujar una
pequeña caja, en cualquier parte, que tenga un flujo resultante saliente o entrante. Por
lo tanto concluimos que
~= ρ
~ ·E
∇
ε0
~ =0
~ ×E
∇
3.2.2.
~ =0
~ ·E
∇
~ =0
~ ·E
∇
~ = µ0~j
~ ×E
∇
Potencial vector
Definiendo el potencial escalar V como
~ =0
~ ×E
∇
(3.38)
~ × (−∇V
~ )=0
∇
(3.39)
~ = −∇V
~ ,
⇒ E
(3.40)
3.2. Ley de Ampere
174
y usando que
~= ρ
~ ·E
∇
ε0
ρ
~
~
∇ · (−∇V ) =
ε0
2
~ V =−ρ,
∇
ε0
entonces definimos el potencial escalar como
Z
ρ(x2 , y2 , z2 )
V (x1 , y1 , z1 ) = ke
dV2 .
r12
(3.41)
(3.42)
(3.43)
(3.44)
~ como
Del mismo modo podemos definir el potencial vector A
~ =0
~ ·E
∇
(3.45)
~ =0
~ · (∇
~ × A)
∇
(3.46)
~ =∇
~
~ × A,
⇒ B
(3.47)
~ = µ0~J
~ ×B
∇
(3.48)
~ = µ0~J.
~ × (∇
~ × A)
∇
(3.49)
y usando que
La ecuación anterior, siendo una ecuación vectorial, en realidad, son tres ecuaciones.
Vamos a desarrollar una de ellas, la ecuación correspondiente a la componente x
∂Ay
∂Ay ∂Ax
∂Az
∂Ax
∂Az
~
~
−
− ̂
−
+ k̂
−
(3.50)
∇ × A = ı̂
∂y
∂z
∂x
∂z
∂x
∂y
∂ ∂Ay ∂Ax
∂ ∂Ax
∂Az
~
~
~
[∇ × (∇ × A)]x =
−
−
−
= µ0 Jx
(3.51)
∂y ∂x
∂y
∂z ∂z
∂x
∂2 Ax
∂2 Ax
∂ ∂Ay
∂ ∂Az
−
−
+
+
= µ0 Jx
(3.52)
∂y2
∂z2
∂x ∂y
∂x ∂z
Para que la ecuación sea más simétrica, sumamos y restamos el mismo término,
∂2 Ax
∂2 Ax
∂2 Ax
∂
−
−
−
+
∂x2
∂y2
∂z2
∂x
∂Ay ∂Az
∂2 Ax
+
+
= µ0~Jx
∂x2
∂y
∂z
∂ ~ ~
−∇2 Ax + (∇
· A) = µ0 Jx ,
∂x
∂2 Ax
,
∂x2
(3.53)
(3.54)
3.2. Ley de Ampere
175
como lo que nos interesa es el rotacional, su divergencia puede ser lo que queramos
~ = 0,
~ ·A
∇
(3.55)
∇2 Ax = −µ0 Jx ,
(3.56)
entonces
de modo que
Ax (x1 , y1 , z1 ) =
µ0
4π
Z
Jx (x2 , y2 , z2 )
dV2 .
r12
(3.57)
Las otras componentes deben satisfacer fórmulas similares, de modo que
~ 1 , y1 , z1 ) = µ0
A(x
4π
Z ~
J(x2 , y2 , z2 )
dV2 .
r12
(3.58)
176
3.2. Ley de Ampere
Ejercicios Propuestos
Magnetismo.
1. Una partícula alfa tiene una velocidad de ν~ = (3ı̂ + 5̂ − 9k̂) [m/s] dentro de un campo
~ = (3ı̂ − 20̂ + 5k̂) [µt]. ¿Cuál es la fuerza que siente la
magnético uniforme dado por B
partícula?.
2. Demuestre que el trabajo realizado por la fuerza magnética sobre una partícula
cargada moviéndose en un campo magnético es cero para cualquier desplazamiento
de la partícula.
3. Un ión con carga +2e tiene una masa de 3, 2 × 10−26 [K g]. Se acelera desde el reposo
por una diferencia de potencial de 900[V ], luego entra en un campo magnético uniforme
de 0, 98 [T ], perpendicularmente.
(a) Calcule la velocidad del ión.
(b) Calcule el radio de su trayectoria dentro del campo magnético.
4. Un protón cuya energía es de 750 [eV ] (1 [eV ] = 1, 6 × 10−26 [J]) está circulando en
un plano formando un ángulo recto con un campo magnético uniforme. El radio de la
trayectoria circular es 0, 8 [m]. Calcule la magnitud del campo magnético.
5. Un alambre de 0, 06 [K g/m] está suspendido por un par de puntas flexibles, como se
muestra en la figura 3.21, dentro de un campo magnético de 440 [mT ]. Determine la
magnitud y dirección de la corriente en el alambre para que la tensión en las puntas
sea cero.
178
Ejercicios propuestos Magnetismo.
Figura 3.21: (Problema 05).
~ = 3ı̂ [T ] hay un segmento de alambre en forma
6. En un campo magnético uniforme B
de L. El alambre lleva una intensidad de corriente de 2 [A], la sección larga mide
3, 6 [m] y forma un ángulo de 60◦ con el eje x, como se muestra en la figura 5.18, y la
sección corta mide 0, 4 [m]. Determine la magnitud y dirección de la fuerza que siente
el alambre debido al campo magnético.
Figura 3.22: (Problema 06).
7. Dos conductores rectos, largos y paralelos, separados por una distancia a llevan una
intensidad de corriente I en la misma dirección. Determine la magnitud y dirección del
campo magnético en un punto P entre los alambres, localizado a una distancia a/4
del alambre de la derecha.
8. Imagine un alambre recto y delgado que lleva una corriente constante I, colocado a lo
largo del eje x. Determine la magnitud y dirección del campo magnético en el punto
Ejercicios propuestos Magnetismo.
179
P generado por esta corriente.
Figura 3.23: (Problema 08).
9. Considere una espira de alambre circular de radio R localizada en el plano yz, y que
transporta una corriente estable I. Calcule el campo magnético en un punto P en el
eje a una distancia x del centro de la espira.
10. Con un alambre de cobre se forma una espira rectangular de 4 [cm] por 10 [cm]. Por la
espira circula una intensidad de corriente de 10 [A]. ¿Cuál es la magnitud del campo
magnético en el centro de la espira?.
11. Un alambre largo está doblado en la forma mostrada en la figura 4.34 y lleva una
corriente de 13 [A]. Utilizando la Ley de Biot-Savart, encuentre la dirección y magnitud
del campo magnético en el punto P, que corresponde al centro de la semicircunferencia
de radio r = 20 [cm].
Figura 3.24: (Problema 11).
12. La figura 5.19 muestra un alambre largo que conduce una intensidad de corriente I1 .
La espira rectangular conduce una intensidad de corriente I2 . Calcule la magnitud y
180
Ejercicios propuestos Magnetismo.
dirección de la fuerza resultante. Suponga que c = 1, 1[cm], a = 9, 2[cm], L = 32, 3[cm],
I1 = 28, 6 [A], I2 = 10 [A].
Figura 3.25: (Problema 12).
13. Suponga dos hilos rectos, largos, coaxiales, aislados y metálicos. Por el hilo interior de
radio a circula una corriente I. Por el hilo que le rodea, de radio interno a y externo 2a,
circula una corriente igual y opuesta, distribuida uniformemente por toda su sección
recta. Calcule el campo magnético en un punto que dista del eje una distancia r cuando:
(a) 0 <r <a
(b) a <r <2a
(c) r >2a
14. Un tubo de 40 [cm] de longitud tiene enrollado sobre él dos bobinas uniformes, una
encima de la otra. Una bobina está enrollada en un sentido y tiene 800 vueltas, mientras
que la otra tiene 300 vueltas y está enrollada en el otro sentido. Encuentre el campo
magnético dentro del solenoide cuando la intensidad de corriente es de 2 [A] en cada
una de las bobinas.
15. Un haz de iones 6 Li y 7 Li pasa a través de un selector de velocidades y entra a un
espectrómetro magnético. Si el diámetro de la órbita de los iones 6 Li es 15 [cm], ¿cuál
es el diámetro de los iones 7 Li?.
Ejercicios propuestos Magnetismo.
181
16. Tres alambres paralelos muy largos están en las esquinas de un cuadrado, de lado L.
Cada alambre lleva una corriente de magnitud I. Encuentre el campo magnético B en
la esquina desocupada del cuadrado cuando:
(a) Todas las corrientes están apuntando hacia dentro del papel.
(b) I1 e I3 están apuntando hacia dentro del papel e I2 hacia fuera. (La notación es
la siguiente: 1 se refiere a la esquina superior izquierda, 2 a la esquina inferior
izquierda y 3 a la esquina inferior derecha. Así, la esquina superior derecha está
desocupada).
(c) I1 e I2 están apuntando hacia dentro del papel e I3 hacia fuera.
182
Ejercicios propuestos Magnetismo.
Capítulo 4
Inducción Electromagnética
a inducción electromagnética es el fenómeno que origina la producción de una fuerza
electromotriz (fem o voltaje) en un medio o cuerpo expuesto a un campo magnético
variable, o bien en un medio móvil respecto a un campo magnético estático. Es así que,
cuando dicho cuerpo es un conductor, se produce una corriente inducida. Este fenómeno
fue descubierto por Michael Faraday quién lo expresó indicando que la magnitud del
voltaje inducido es proporcional a la variación del flujo magnético.
L
4.1.
Ley de inducción de Faraday
asta ahora nuestro estudio sobre la electricidad y magnetismo se ha limitado a los
campos eléctricos producidos por cargas estacionarias y a los campos magnéticos
generados por cargas en movimiento. Vamos a estudiar los efectos causados por campos
magnéticos que varían con el tiempo.
H
Los experimentos de Michael Faraday en Inglaterra en 1831 y los efectuados de forma
independiente por Joseph Henry ese mismo año, mostraron que es posible inducir una
fem en un circuito utilizando un campo magnético variable en el tiempo.
Consideremos una espira de alambre conectada a un amperímetro sensible.
184
4.1. Ley de inducción de Faraday
(a) Cuando el imán se mueve hacia la espira, ésta genera una corriente, moviéndose la
aguja del galvanómetro.
(b) Cuando el imán se mueve alejándose de la espira, ésta genera una corriente opuesta
a como se muestra en a).
Figura 4.1: Inducción de una fem utilizando un campo magnético
variable.
(a) Cuando el imán se acerca a la espira, la aguja se desvía en una dirección.
(b) En cuanto se deja el imán en reposo y se le mantiene estacionario en relación con
4.1. Ley de inducción de Faraday
185
la espira, no se observa deflexión alguna
(c) Cuando el imán es alejado de la espira, la aguja se desvía en la dirección opuesta.
Finalmente, si el imán se mantiene estacionario y la espira se mueve ya sea hacia el
imán o en la dirección opuesta, la aguja se desviará.
Es así como podemos concluir que se establece una corriente a pesar de que no existe
una batería presente en el circuito.
4.1.1.
¿Cómo Faraday dedujo la Ley de Inducción?
Una bobina primaria se conecta a un interruptor y a una batería. La bobina se enrolla
alrededor de un anillo de hierro, y una corriente a través de la bobina producirá un
campo magnético al cerrarse el interruptor. Una bobina secundaria también está enrollada
alrededor del anillo y se encuentra conectada a un amperímetro sensible.
Figura 4.2: Experimento de Faraday.
Cuando se abre o se cierra el interruptor ocurre algo bastante asombroso.
En el momento en que se cierra el interruptor, la aguja se mueve en una dirección
4.1. Ley de inducción de Faraday
186
y de inmediato regresa a cero. En el instante en que el interruptor se abre, la aguja se
mueve en la dirección opuesta y de nuevo vuelve a cero.
De este modo se puede concluir que la corriente en el circuito primario genera un
campo magnético que penetra en el circuito secundario.
4.1.2.
Ley de Gauss en Magnetismo
El flujo eléctrico a través de una superficie cerrada que rodea una carga neta es
proporcional a dicha carga. Es así como el número de líneas de campo eléctrico que
salen de la superficie depende únicamente de la carga neta que se encuentra en su
interior. Las líneas de campo eléctrico se originan y terminan en cargas eléctricas.
Figura 4.3: Líneas de campo eléctrico de un dipolo eléctrico se inician
en la carga positiva y terminan en la carga negativa.
Las líneas de campo magnético no empiezan ni terminan en ningún punto. Así, el
número de líneas que entran a la superficie es igual al número de líneas que salen, por
lo tanto, el flujo magnético neto es igual a cero.
4.1. Ley de inducción de Faraday
187
Figura 4.4: Líneas de campo magnético de un imán de barra formando
lazos cerrados.
La ley de Gauss en el magnetismo establece que el flujo magnético neto a través de
cualquier superficie cerrada es siempre igual a cero.
I
φ=
4.1.3.
S
~ · dS
~ =0
B
(4.1)
Ley de Inducción
En un circuito es posible inducir una corriente eléctrica mediante un campo magnético
variable en el tiempo. La fem inducida en un circuito es directamente proporcional a la
rapidez de cambio del flujo magnético a través del circuito.
~
Consideremos una única espira C , inmersa en un campo magnético B
4.1. Ley de inducción de Faraday
188
Figura 4.5: Espira inmersa en un campo magnético.
~ a través de la espira es
El flujo de B
Z
Z
~
~
~ · n̂dS = 0.
φ=
B · dS =
B
S
S
(4.2)
Supongamos que R es la resistencia de la espira C . La Ley de Faraday puede entonces
ser enunciada en términos de la corriente I inducida en C cuando φ varia con el tiempo:
I=−
1 dφ
.
R dt
(4.3)
La existencia de esta corriente en la espira esta asociada a una fem ε dada por
ε = RI = −
4.1.3.1.
dφ
.
dt
(4.4)
Ejemplo
Una espira de alambre que encierra una superficie A se coloca en una región donde
~ varía con
el campo magnético es perpendicular al plano de la espira. La magnitud de B
el tiempo según B = B0 e−at , siendo a una constante. Determine la fem inducida en la
espira como función del tiempo.
Solución
I
I
d
d
dB
dA
dB
dφ
d
~ · dA
~=−
ε=−
=−
B
B dA = − (BA) = −A
−B
= −A
dt
dt A
dt
dt
dt
dt
dt
A
−at
dB0 e
ε = −A
= aAB0 e−at
dt
4.1. Ley de inducción de Faraday
4.1.4.
189
Aplicación de la Ley de Faraday
Una aplicación interesante es el sonido que produce una guitarra eléctrica.
En este caso la bobina, llamada bobina de toma, se coloca cerca de la cuerda de
la guitarra, que está fabricada de un material magnetizable. Un imán permanente en el
interior de la bobina magnetiza la porción de la cuerda más cercana. Cuando la cuerda
vibra con cierta frecuencia, su segmento magnetizado produce un flujo magnético variable
a través de la bobina. Este flujo induce una fem en la bobina que alimenta el amplificador
Figura 4.6: Una cuerda de guitarra eléctrica, que vibra, induce una fem
en una bobina de la recolectora.
La variación del flujo φ con el tiempo puede deberse a:
~ constante
Al movimiento de la curva C a través de un campo magnético B
~ con el tiempo
A la variación de B
A una deformación del circuito C .
El resultado sólo depende de la tasa de variación de flujo magnético como función del
tiempo, cualquiera sea el origen de esta variación.
4.1. Ley de inducción de Faraday
190
4.1.5.
Circuito moviéndose en un campo magnético fijo
~ fijo, los electrones
Si un hilo se mueve con velocidad ν~ en un campo magnético B
libres están sujetos a la fuerza de Lorentz
~
F~ = −e~
ν × B.
(4.5)
Como esta es una fuerza de origen "no-electrostática", podemos asociarle a ella un "
~ (e) dado por
campo eléctrico equivalente" E
~ (e)
F~ = −e~
νE
(4.6)
~ (e) = ν~ × B.
~
⇒ E
La fuerza electromotriz a lo largo del circuito C es entonces
I
I
(e)
~ · d~l = (~
~ · d~l.
ε=
E
ν × B)
C
C
(4.7)
(4.8)
Para relacionar esta expresión con la variación del flujo magnético φ, consideraremos
dos posiciones sucesivas de C , en los instantes t y t + dt. Durante el intervalo de tiempo
dt, cada punto de C sufre un desplazamiento ν~ dt.
Figura 4.7: Dos posiciones sucesivas de C para relacionar la variación
del flujo magnético con la fuerza electromotriz.
4.1. Ley de inducción de Faraday
191
El producto vectorial es
~l.
d~l × ν~ dt = n̂l dA = dA
(4.9)
Las superficies de las bases, At y At+dt , forman en conjunto con Al , un cilindro cerrado
A ≡ At + At+dt + Al
(4.10)
y tenemos entonces
Z
Z
~ · n̂l dA = 0
~
~
B
B · n̂t+dt dA −
B · n̂t dA +
At
Al+dl
At+dt
Z
Z
~ · n̂t+dt dA −
~ · n̂t dA +
~ ·B
~ =0
B
B
d~l × (νdt)
At+dt
At
C
I
~ = 0,
φt+dt − φt + dt (d~l × ν~ · B)
I
~ · dA
~=0=
B
A
Z
Z
C
(4.11)
(4.12)
(4.13)
despejando tenemos
I
dt
C
~ = −(φt+dt − φt ) = −dφ,
(d~l × ν~ ) · B
(4.14)
de manera que
I
~ = −dφ
d~l · (~
ν × B)
I
~ (e) = −dφ
dt
d~l · E
IC
~ (e) = − dφ
⇒ ε=
d~l · E
dt
C
dt
(4.15)
C
4.1.5.1.
(4.16)
Forma Integral de la Ley de Inducción.
(4.17)
Ejemplo
Un solenoide largo de radio R tiene n vueltas de alambre por unidad de longitud y
lleva una corriente variable en el tiempo dada por I = I0 cos ωt , donde I0 es la corriente
máxima y ω es la frecuencia angular de la fuente de corriente alterna. Recuerde que el
campo magnético de un solenoide es B = µ0 nI = µ0 nI0 cos ωt
(a) Determine la magnitud del campo eléctrico inducido a una distancia r > R a lo largo
4.1. Ley de inducción de Faraday
192
de su eje central.
I
I
d
~
~
~ · d~s
E · dl = −
B
dt S
C
I
I
d
⇒ E
dl = −
B ds
dt
C
S
d
⇒ E(2πr) = − [µ0 nI0 cos ωt(πR 2 )]
dt
⇒ E(2
πr) = µ0 nI0
πR 2 w sin ωt
⇒ E=
µ0 nI0 R 2 w
sin ωt
2r
(b) ¿Cuál es la magnitud del campo eléctrico inducido en el interior del solenoide, a una
distancia r < R de su eje central?.
I
I
d
~ · d~s
~
~
B
E · dl = −
dt S
C
I
I
d
B ds
⇒ E
dl = −
dt
S
C
d
⇒ E(2πr) = − [µ0 nI0 cos ωt(πr 2 )]
dt
⇒ E(2
π r)
πr2 w sin ωt
= µ0 nI0
⇒ E=
4.1.6.
µ0 nI0 w
r sin ωt
2
Circuito fijo y un campo magnético variable
~ el que varía con el tiempo, no existe fuerza
Si el circuito C permanece fijo y es B
de Lorentz sobre los electrones, mas la experiencia muestra que el resultado permanece
válido
Z
Z ~
dφ
d
~ · dA
~ = − ∂B · dA,
~
ε=−
=−
B
(4.18)
dt
dt A
A ∂t
vemos entonces que
~
∂B
~
· dA,
∂t
(4.19)
pero por el teorema del rotacional
I
Z
~
~
~ · dA,
~
~ × E)
E · d l = − (∇
(4.20)
I
ε=
C
C
~ · d~l = −
E
A
Z
A
4.1. Ley de inducción de Faraday
193
de modo que
~
~ = − ∂B .
~ ×E
∇
∂t
4.1.7.
(4.21)
Ley de Lenz
Vamos ahora a discutir la interpretación del signo (-) en la Ley de Inducción de
Faraday, que se debe a H. Lenz (1834)
d
dφ
=−
ε=−
dt
dt
Z
S
~ · dS
~ =−
B
Z
S
~
∂B
~
· dS.
∂t
(4.22)
Consideremos una espira conductora C orientada con una normal n̂ a su plano, y
supongamos que se aproxima a ella un imán permanente, con su polo Norte apuntando
hacia la espira
Figura 4.8: Imán que se mueve hacia una espira conductora, donde se
induce una corriente.
~ del imán tiende a ser antiparalelo a n̂, tenemos que B
~ · n̂ < 0 y el
Como el campo B
flujo φ del campo del imán a través de la curva C es φ < 0. A medida que el imán se
aproxima, |φ| aumenta, de modo que para φ < 0 implica que tendremos
dφ
< 0.
dt
(4.23)
4.1. Ley de inducción de Faraday
194
Debido al signo (-) en la Ley de Inducción, tenemos que la fem inducida es positiva
I
~ · d~l = − dφ > 0
ε=
E
(4.24)
dt
C
~ dentro de la espira es tal que
o sea, el campo E
~ · d~l > 0.
E
(4.25)
De este modo, la corriente inducida I tendrá la orientación de d~l. Esto es equivalente
a crear en la espira un dipolo magnético cuya cara Norte apunta hacia la cara Norte
del imán, produciendo una fuerza magnética de repulsión sobre el imán, oponiéndose al
movimiento del imán.
Importante: el sentido de la corriente inducida es aquél que tiende a oponerse a la
variación de flujo a través de la espira.
Si el imán se aparta de la espira, entonces
dφ
>0
dt
y la fem inducida será
I
~ · d~l = − dφ < 0.
ε=
E
dt
C
(4.26)
(4.27)
La cara Sur del dipolo correspondiente apunta ahora hacia el imán, tendiendo a
atraerlo de vuelta, o sea, nuevamente se opone a la variación de flujo a través de la curva
C.
Figura 4.9: La corriente inducida produce su propio flujo hacia la
izquierda, para contrarrestar el incremento del flujo externo hacia la
derecha.
4.1. Ley de inducción de Faraday
195
La Ley de Lenz está directamente relacionada al principio de conservación de la
energía.
En el ejemplo del imán cuya cara norte se aproxima a la espira, una corriente en
sentido opuesto a la corriente que sigue la Ley de Lenz crearía una cara Sur en la
espira, atrayendo al imán hacia ella y acelerando su movimiento. El imán generaría
energía cinética y al mismo tiempo produciría calor a través de la corriente inducida,
violando la ley de conservación de la energía.
Importante: La energía disipada por la corriente inducida (calor) debe obtenerse
mediante una disminución de la energía cinética del imán.
4.1.8.
Fem en movimiento
Fem de movimiento es la fem inducida en un conductor en movimiento a través de un
campo magnético constante.
Figura 4.10: Barra conductora moviéndose con una velocidad ν~ a través
~
de un campo magnético B.
La figura muestra un conductor eléctrico recto de longitud l que se mueve con una
~ Debido a la fuerza magnética
velocidad ν~ a través de un campo magnético uniforme B.
ejercida sobre los electrones, los extremos del conductor se cargan con cargas opuestas.
Esto establece un campo eléctrico en el conductor. En estado estable, las fuerzas
4.1. Ley de inducción de Faraday
196
eléctricas y magnéticas presentes en el alambre se equilibran
)
~ ⇒ |F~e | = qE
F~e = qE
E = νB
~ ⇒ |F~B | = qνB
F~B = q~
ν×B
(4.28)
El campo eléctrico que se produce en el conductor está relacionado con la diferencia
de potencial en los extremos
Z
~ · d~l = El = BLν.
(4.29)
∆V = E
Importante: Se mantiene una diferencia de potencial entre los extremos del
conductor siempre que éste se siga moviendo a través del campo magnético uniforme.
Una situación más interesante se presenta cuando el conductor en movimiento forma
parte de una trayectoria de conducción cerrada
Figura 4.11: Barra conductora deslizándose a lo largo de dos rieles
conductores. La fuerza magnética F~m se opone al movimiento y un
corriente se induce en la espira en la dirección contraria a las
manecillas del reloj.
Si la normal n̂ al plano del circuito está orientada hacia arriba, el flujo del campo es
I
I
~
~
~ · n̂dS = −Blx,
φ=
B · dS =
B
(4.30)
S
S
luego la fem inducida está dada por
ε=−
dφ
dx
= Bl
= Blν.
dt
dt
(4.31)
4.1. Ley de inducción de Faraday
197
La corriente inducida tiene así la forma
I=
ε
Blν
IR
=
⇒ ν=
.
R
R
Bl
(4.32)
~ actúa sobre el conductor
La fuerza magnética F~B con la cual el campo magnético B
móvil está dada por
Z
~
~ = −IlB ν~
FB = I d~l × B
(4.33)
ν
l2 B 2
ν~ .
(4.34)
⇒ F~B = −
R
Si quisiéramos mantener el conductor móvil bajo una velocidad constante, tendríamos
que ejercer una fuerza dada por
F~ = −F~B ,
(4.35)
el trabajo realizado por esta fuerza F~ por unidad de tiempo (potencia mecánica) es
dW
l2 B 2 2
= F~ · ν~ =
ν .
dt
R
(4.36)
Por otro lado, la potencia disipada por la corriente inducida (efecto Joule) es
P = εI = Blν ·
Blν
l2 B 2 2
=
ν .
R
R
(4.37)
Vemos que el resultado es consistente con el principio de conservación de la energía:
la potencia producida por el trabajo mecánico de empujar el conductor móvil es igual a
la potencia disipada en forma de calor por el efecto Joule. Esto concuerda con la Ley de
Lenz.
4.1.8.1.
Ejemplo
Una barra conductora se nueve sobre dos rieles paralelos libres de fricción en
presencia de un campo magnético uniforme dirigido hacia la página. La barra tiene una
masa m y su longitud es L. A la barra se le imprime una velocidad inicial ν~i hacia la
derecha y se libera en t = 0 [s]. Utilizando las Leyes de Newton encuentre la velocidad
de la barra como función del tiempo.
4.1. Ley de inducción de Faraday
198
Solución
ε=−
dφ
d
=−
dt
dt
⇒ ε = Blν
⇒ I=
I
~ · d~s = − d (−BLx) = Blν
B
dt
S
· 1/R
ε
Blν
=
R
R
F~B = I
Z
~ = −ILB ν~
d~l × B
ν
⇒ F~B = −ILB
dν
= −ILB
dt
B 2 L2
dν
=−
ν
⇒ m
dt
R
2 2Z t
Z ν
dν
B L
⇒
=−
dt
mR
νi ν
0
B 2 L2
t
ν
t=−
=−
⇒ ln
νi
mR
τ
Fx = ma = m
⇒ ν(t) = νi e−t/τ
4.1.9.
donde τ =
mR
B 2 L2
Generadores y motores
En el ejemplo anterior vimos que una potencia mecánica se convierte en una corriente
eléctrica I, que permanece constante mientras la barra se mantenga en movimiento con
~ Tenemos así un generador
una velocidad ν constante, dentro de un campo uniforme B.
lineal de corriente continua, que no es muy práctico porque deja de funcionar cuando el
alambre en movimiento sale de la región del campo magnético.
Una adaptación del mismo circuito ilustra el principio básico de un motor de inducción.
4.1. Ley de inducción de Faraday
199
Figura 4.12: Motor de inducción.[4]
Una batería genera una diferencia de potencial V , haciendo pasar una corriente I en
el sentido horario. La fuerza magnética F~B apunta hacia la derecha, y es equilibrada por
la fuerza peso m~
g, permitiendo que la barra se mueva hacia la derecha con velocidad
constante. De este modo tendremos que
I
I
~
~
~ · n̂dS = BLx
φ=
B · dS =
B
(4.38)
S
S
dφ
dx
⇒ ε=−
= −BL
= −BLν
(4.39)
dt
dt
Como la fem inducida tiene signo contrario a la fem V de la batería, recibe el nombre de
fuerza contra-electromotriz. La intensidad de corriente es entonces:
V − BLν
(4.40)
I=
R
Sin embargo, nos falta determinar la velocidad ν. La fuerza magnética es equilibrada por
la fuerza peso. De este modo,
Z
~ = IBL = V − BLν LB = mg
|F~B | = I |d~l × B|
(4.41)
R
R
R V
mg
⇒ ν=
−
(4.42)
LB R
LB
luego
V − BLν
V
I=
= −
R
R
mg
I=
LB
V
mg
−
R
LB
(4.43)
(4.44)
4.1. Ley de inducción de Faraday
200
La potencia eléctrica generada por la batería para alimentar el motor es V I. Parte de ella
es convertida en energía mecánica, haciendo subir el peso m con velocidad ν, y parte es
disipada en calor por el efecto Joule (I 2 R)
V I = mgν + I 2 R
(4.45)
p. eléctrica = p. mecánica + p. disipada
Este es el balance típico de un motor.
4.1.10.
Generación de corriente alterna
Figura 4.13: Diagrama de un generador de corriente AC.[4]
El cuadro de área S (normal n̂) esta formado de N espiras (N = 2), y gira dentro
~ con velocidad angular constante ω, de modo que el
de un campo magnético uniforme B,
~ y la normal n̂ esta dado por
ángulo θ entre B
θ = ωt
(4.46)
~ ·S
~ = NBS cos θ = NBS cos(ωt)
φ = NB
(4.47)
El flujo a través de las espiras es
La fem inducida es, por lo tanto
ε=−
dφ
= ωNBS sin ωt
dt
(4.48)
4.1. Ley de inducción de Faraday
201
Figura 4.14: Gráfico de fem alterna en función del tiempo.
Si la resistencia externa es R, la corriente I será
I=
4.1.11.
ωNBS
ε
=
sin ωt
R
R
(4.49)
Corrientes de Foucault
Si una espira conductora se suelta y queda libre sobre un imán permanente, la
corriente I inducida creará un dipolo magnético que será repelido por el imán, produciendo
una fuerza F~ de frenado de la espira.
Análogamente, consideremos un péndulo metálico suspendido de un punto P que,
durante sus oscilaciones, penetra en una región donde existe un campo magnético.
202
4.1. Ley de inducción de Faraday
Figura 4.15: Placa conductora que entra al campo en la posición 1, la
corriente de Foucault es contraria a las manecillas del reloj.
Entonces, serán inducidas en el disco metálico corrientes que tienden a oponerse a
la variación de flujo a través de él. Estas corrientes de Foucault equivalen a una fuerza
de roce de un material viscoso. Podemos reducir este efecto cortando una serie de franjas
en el disco del péndulo.
Figura 4.16: Placa del péndulo con ranuras que reducen las corrientes
de Foucault.
4.1. Ley de inducción de Faraday
203
Con estos cortes, reducimos el flujo en las partes metálicas, y al mismo tiempo
obligamos a cada corriente a recorrer un camino más largo, aumentando la resistencia y
disminuyendo las corrientes de Foucault.
Los sistemas de frenado en muchos trenes subterráneos (como por ejemplo el metro
de Santiago) aprovechan la inducción electromagnética y las corrientes de Foucault. Un
electroimán sujeto al tren está colocado cerca de los rieles de acero.
El efecto de frenado se presenta cuando se hace pasar una corriente muy grande por
el electroimán. El movimiento relativo existente entre el imán y los rieles induce en estos
corrientes de Foucault, y la dirección de estas corrientes produce una fuerza de arrastre
sobre el tren en movimiento. Dado que estas corrientes disminuyen uniformemente en
magnitud al disminuir la velocidad del tren, el efecto de frenado es muy suave.
4.1.12.
Inductancia Mutua y Autoinductancia
Una de las experiencias de Faraday consistió en inducir una corriente en una bobina
variando la corriente en otra bobina: el flujo magnético producido actúa sobre la otra
bobina y su variación genera una corriente.
Consideremos dos solenoides coaxiales muy largos, del mismo largo L, uno de radio
R1 y N1 espiras, y el otro de radio R2 > R1 y N2 espiras. Si hacemos pasar una corriente
~ 1 que produce está dado por
I1 estacionaria por el solenoide 1 (de radio R1 ), el campo B

N1


 µ0 L I1 k̂
~1 =
B



0
0 ≤ r ≤ R1
(4.50)
r > R1
~ 1 sobre las N2 espiras del solenoide 2 es
El flujo φ2(1) producido por B
Z
φ2(1) = N2
~ 1 · k̂dS = N2 B1 (πR 2 ) = µ0 N1 N2 (πR 2 )I1
B
1
1
L
S2
φ2(1) ≡ L21 I1 ,
(4.51)
(4.52)
de modo que
L21 = µ0 N1 N2
πR12
L
Inductancia Mutua.
(4.53)
4.1. Ley de inducción de Faraday
204
La unidad de inductancia es el Henry, definido por
1H ≡ 1
Wb
.
A
(4.54)
Análogamente, si hacemos pasar una corriente estacionaria I2 por el solenoide 2,
produciremos un campo

N2


0 ≤ r ≤ R2
 µ0 L I2 k̂
~
B2 =
(4.55)



0
r > R2
y ell flujo φ1(2) de este campo en las N1 espiras del solenoide 1 es
Z
~ 2 · k̂dS = N1 B2 (πR 2 ) = µ0 N1 N2 (πR 2 )I2
φ1(2) = N1
B
1
1
L
S1
φ1(2) ≡ L12 I2 ,
(4.56)
(4.57)
donde
πR12
,
L
donde podemos concluir dadas las ecuaciones (4.58) y (4.53), que
L21 = µ0 N1 N2
L12 = L21 .
(4.58)
(4.59)
Justificando el nombre de inductancia mutua. (Note que L12 no se obtiene sustituyendo
1 por 2 en L21 ).
Además de producir un flujo magnético en el solenoide 2, la corriente I1 también
produce un flujo φ1(1) en el propio solenoide 1
Z
2
~ 1 · k̂dS = N1 B1 (πR 2 ) = µ0 N1 (πR 2 )I1
φ1(1) = N1
B
(4.60)
1
1
L
S1
φ1(1) = L1 I1 ,
donde
L1 ≡ L11 = µ0
(4.61)
N12
(πR12 )
L
Autoinductancia solenoide 1.
(4.62)
Análogamente, la corriente I2 produce un flujo φ2(2) en el solenoide 2 por donde ella
pasa, dado por
Z
2
~ 2 · k̂dS = N2 B2 (πR 2 ) = µ0 N2 (πR 2 )I2
B
φ2(2) = N2
(4.63)
2
2
L
S2
φ2(2) = L2 I2 ,
(4.64)
4.1. Ley de inducción de Faraday
donde
L2 ≡ L22 = µ0
205
N22
(πR22 )
L
Autoinductancia solenoide 2.
(4.65)
Note que las autoinductancias y la inductancia mutua están dadas sólo por factores
geométricos.
Si pasa simultáneamente una corriente I1 por el solenoide 1 y una corriente I2 por el
solenoide 2, los flujos magnéticos correspondientes a través de los dos solenoides serán
φ1 = L1 I1 + L12 I2
(4.66)
φ2 = L2 I2 + L21 I1 .
(4.67)
Como conclusión podemos obtener la siguiente relación
(N1 N2 )2 2
π (R1 R2 )2
L2
p
(N1 N2 )
R2
L1 L2 = µ0
π(R1 R2 ) = L12
L
R1
p
R2
⇒
L1 L2 = L12
R1
L
R
√ 12 = 2 < 1
R1
L1 L2
L1 L2 = µ02
(4.68)
(4.69)
(4.70)
(4.71)
Podemos entonces concluir a partir de la ley de inducción que, si I2 (t) es una corriente
variable en el circuito 2, la fem ε1 inducida por esa variación en el circuito 1 será
ε1 = −
d
dI2 (t)
φ1(2) = −L12
,
dt
dt
(4.72)
donde L12 es la inductancia mutua entre los dos circuito. Análogamente, si I1 (t) es una
corriente variable en 1, la fem inducida ε2 en el circuito 2 es
ε2 = −
dI1 (t)
d
φ2(1) = −L21
.
dt
dt
(4.73)
Análogamente, la variación de I1 con el tiempo produce una fem autoinducida en el
circuito 1 dada por
dI1 (t)
ε1 = −L1
,
(4.74)
dt
y correspondientemente
dI2 (t)
ε2 = −L2
.
(4.75)
dt
4.1. Ley de inducción de Faraday
206
Es importante recordar que una fem es positiva cuando tiene el mismo sentido que
la corriente en el circuito donde actúa. Como la fem de la ley de Faraday se opone a la
variación de la corriente
dI
> 0,
dt
(4.76)
debe implicar que ε < 0; luego, las autoinductancias, como L1 y L2 , son siempre
positivas de acuerdo con esta convención. Para L12 , su signo depende de las convenciones
adoptadas para los signos de I1 e I2 en los circuitos, de forma que L12 puede ser positivo
o negativo.
En el caso en que tengamos corrientes variables en los dos circuitos, las fem inducidas
serán entonces
dI2 (t)
dI1 (t)
− L12
dt
dt
dI1 (t)
dI2 (t)
ε2 = −L21
− L2
.
dt
dt
ε1 = −L1
4.1.12.1.
(4.77)
(4.78)
Ejemplo
Un cable coaxial está constituido por un hilo conductor cilíndrico de radio a envuelto
por una capa cilíndrica conductora de radio b (separados por un aislante, donde podemos
~ como en el vacío). Una corriente de intensidad I es transmitida axialmente a
calcular B
lo largo del conductor interno, y regresa por el externo. Calcule la autoinductancia del
cable coaxial.
4.1. Ley de inducción de Faraday
207
Figura 4.17: Corte seccional de un cable coaxial largo.
Solución
~ son círculos concéntricos, orientados como en
Por simetría, las líneas de fuerza de B
~ es constante a lo largo de esta curva. Así, por la ley de Ampere tendremos,
la figura, y |B|
I
I
~ · d~l = B
B
dl = 2πrB = µ0 I
C
C
⇒ 2πrB = µ0 I
~ = µ0 I φ̂
⇒ B
2πr
donde φ̂ es un vector unitario tangente al circulo. Asumiendo que a b, podemos
~ a través de un rectángulo
despreciar el flujo contenido en el hilo interno. El flujo de B
que une el conductor interno con el externo es
Z
Z b
µ
Il
b
0
~ · φ̂ds = l
φ= B
B(r)dr =
ln
2π
a
a
φ
b
µ0
o sea, el flujo por unidad de longitud es
= LI, donde L =
ln
es la
l
2π
a
4.1. Ley de inducción de Faraday
208
autoinductancia del cable coaxial por unidad de longitud.
4.1.12.2.
Ejemplo
Consideremos una bobina toroidal de N1 espiras; el toroide tiene radio medio a y
radio de sección circular b. Calcule la autoinductancia del toroide.
Solución
La línea de fuerza que pasa por un punto P es un círculo de radio r = PP 0 con
r = a − ρ cos φ, y la ley de Ampere, para este punto es
I
I
~
~
B · dl = B
dl = 2πrB = µ0 N1 I
C
C
donde N1 es el número de espiras de la bobina enrollada en el toroide e I es la intensidad
de corriente que lo atraviesa.
1
~ φ) = µ0 N1 I
n̂
B(ρ,
2π (a − ρ cos φ)
donde n̂ es el vector unitario normal al plano de la sección. El flujo a través de una espira
(sección transversal) es
Z
Z
Z 2π
dφ
µ0 N1 I b
~
φ1 = B · n̂ds =
ρdρ
2π
(a − ρ cos φ)
0
A
!0
Z b
µ0 N1 I
2π
φ1 = ρdρ p
2π
a2 − ρ2
0
Z b
ρ
p
φ1 = µ0 N1 I
dρ
2
a − ρ2
0
p
φ1 = µ0 N1 I(a − a2 − b2 )
Si hubiese una segunda bobina con N2 espiras enrolladas en el toroide, el flujo producido
por la primera en la segunda es entonces N2 φ1 , de modo que
p
L12 = µ0 N1 N2 (a − a2 − b2 )
para la inductancia mutua entre las dos bobinas enrolladas en el mismo toroide.
Análogamente, la autoinductancia de una bobina toroidal de N1 espiras es
p
L = µ0 N12 (a − a2 − b2 )
4.1. Ley de inducción de Faraday
4.1.13.
209
Energía magnética
Acabamos de ver que la fuerza electromotriz inducida ε en un circuito debido a un
campo magnético variable tiende a oponerse a la variación de flujo
ε=−
dφ
.
dt
(4.79)
Si la corriente en un instante considerado es I, la potencia necesaria para eso es
P=
dW
dφ
dI
= −εI =
I = LI ,
dt
dt
dt
(4.80)
donde L es la autoinductancia del circuito. Ignorando la pérdida por efecto Joule
(suponiendo despreciable la resistencia del circuito), la energía total que es necesaria
para hacer pasar una corriente I en un tiempo t es
Z
U=
0
t
dW
dt =
dt
Z
t
LI
0
dI
dt = L
dt
Z
t
IdI =
0
1 2
LI ,
2
(4.81)
que es la energía almacenada en un circuito de autoinductancia L que es atravesado por
una corriente I.
Si tuviésemos dos circuitos, podemos, en principio, producir una corriente I1 en uno
de ellos (en el otro con corriente I = 0), almacenando una energía
U1 =
1 2
L1 I ,
2 1
(4.82)
después podemos aumentar la corriente en el circuito 2 desde I = 0 hasta I = I2 ,
introduciendo una energía
Z
Z
dφ1(2)
dW
dφ2
dt = I2
dt + I1
dt
dt
dt
dt
Z
Z
Z
dW
dL2
dL2
dt = I2 L2
dt + I1 L12
dt
dt
dt
dt
1
⇒ U2 = L2 I22 + L12 I1 I2 ,
2
Z
(4.83)
(4.84)
(4.85)
de modo que la energía total será
U = U1 + U2 =
1 2 1 2
L1 I + L2 I + L12 I1 I2 .
2 1 2 2
(4.86)
4.1. Ley de inducción de Faraday
210
4.1.14.
Densidad de energía magnética
Vimos que la autoinductancia de un solenoide de largo l, área de sección S y con N
espiras es
S
(4.87)
L = µ0 N 2 ,
l
de modo que, cuando tenemos una corriente I, la energía almacenada es
N 2
S
1
1
1
B2
Um = LI 2 = µ0 (NI)2 =
µ0 I sl =
V,
(4.88)
2
2
l
2µ0
l
2µ0
de manera que la densidad de energía magnética es
Um
B2
=
.
V
2µ0
µm ≡
(4.89)
Si tuviésemos al mismo tiempo, una región del espacio con un campo eléctrico y un
campo magnético, la densidad de energía electromagnética total es
µ = µe + µm =
4.1.14.1.
ε0 E 2
B2
+
.
2
2µ0
(4.90)
Ejemplo
Calcule la energía almacenada en un cable axial.
Solución
~ son círculos concéntricos y |B|
~ es constante a
Por simetría, las líneas de fuerza de B
lo largo de la curva C . Así, por la ley de Ampere tendremos
I
I
~
~
B · dl = B
dl = 2πρB = µ0 I
C
C
~ = µ0 I φ̂
B
2πρ
donde
~2
1
|B|
=
µm =
2µ0
2µ0
De esta manera tendremos que
Z b
Z
Z
Z z0 +l
µm dν =
dz
ρdρ
z0
a
0
2π
µ0 I
2πρ
2
µm dφ =
=
µ0 I 2
8π 2 ρ2
µ0 2
I l
4π
Z
b
a
dρ
µ0 2
=
I l ln
ρ
4π
b
a
4.1. Ley de inducción de Faraday
211
de modo que la energía magnética almacenada por unidad de longitud es
U
1 µ0
=
ln
l
2 2π
4.1.15.
b 2 1L 2
I =
I
a
2l
µ0
b
L
=
ln
l
2π
a
Circuitos RL
Si un circuito contiene una bobina, como por ejemplo un solenoide, la autoinductancia
de ésta impide que la corriente en el circuito aumente o disminuya de manera instantánea.
Dado que la inductancia en un inductor resulta en una fuerza contraelectromotriz, un
inductor en un circuito se opone a los cambios en la corriente dentro de dicho circuito.
Por lo tanto, el inductor hace que el circuito tarde en reaccionar a los cambios en el
voltaje.
Figura 4.18: Circuito RL en serie.
Suponga que el interruptor se abre en t < 0 y se cierra después en t = 0. La
corriente en el circuito comienza a aumentar y se induce en el inductor una fuerza
contraelectromotriz que se opone a la corriente en aumento. Usando la ley de mallas de
Kirchhoff tenemos
ε − IR − L
dI
= 0.
dt
(4.91)
4.1. Ley de inducción de Faraday
212
Vamos a realizar el cambio de variable
ε
−I
R
dx
dI
=− ,
dt
dt
x=
(4.92)
(4.93)
de modo que
ε
L dI
−I −
=0
R
R dt
L dI
x+
=0
R dt
Z
Z x
R t
dx
dt
=−
L 0
x0 x
x
R
ln
=− t
x0
L
(4.94)
(4.95)
(4.96)
(4.97)
⇒ x = x0 e−Rt/L .
(4.98)
Debido a que I = 0 en t = 0, entonces x0 = ε/R. En consecuencia
ε
ε
− I = e−Rt/L
R
R
ε
I=
1 − e−Rt/L
R
⇒ I(t) = I0 1 − e−t/τ
(4.99)
(4.100)
donde τ =
L
ε
, I0 = .
R
R
(4.101)
Esta expresión muestra como la corriente es afectada por la presencia del inductor.
Analicemos ahora el siguiente circuito
Figura 4.19: Circuito RL con dos interruptores. Cuando S1 esta cerrad
y S2 esta abierto, la batería forma parte del circuito.
4.1. Ley de inducción de Faraday
213
Suponga que el interruptor S1 se ha colocado cerrado mientras que el interruptor S2
esta abierto durante un tiempo suficiente para permitir que la corriente llegue a su valor
de equilibrio ε/R. Si el interruptor S1 se abre y el S2 se cierra, tenemos un circuito sin
batería. Usando la ley de mallas de Kirchhoff tenemos
dI
=0
dt
dI
R
=− I
dt
L
Z I
Z
Z
1 τ
dI
R t
dt = −
dt
=−
L 0
τ 0
I0 I
I
t
ln
=−
I0
τ
ε
⇒ I(t) = I0 et/τ = e−t/τ .
R
IR + L
(4.102)
(4.103)
(4.104)
(4.105)
(4.106)
Si el circuito no incluyera un inductor, la corriente se reduciría inmediatamente a
cero al eliminar la batería.
4.1.16.
Oscilaciones libres en un circuito LC
Consideremos un circuito idealizado que consiste exclusivamente de un capacitor de
capacitancia C y un inductor de inductancia L.
Figura 4.20: Circuito LC en serie.
Como despreciamos completamente la resistencia, no existe disipación, y la energía
inicialmente almacenada en el sistema se conserva. Podemos considerar, por ejemplo,
que esa energía corresponde a la carga inicial del capacitor. Usando la ley de Kirchhoff
tenemos
Q
dI
+L
= 0,
(4.107)
C
dt
4.1. Ley de inducción de Faraday
214
derivando con respecto al tiempo tenemos
1 dQ
d2 I
+L 2 =0
C dt
dt
d2 I
+ ω02 I = 0,
dt 2
(4.108)
(4.109)
√
donde ω = 1/ LC es la frecuencia angular de las oscilaciones libres en este circuito.
La ecuación anterior es la ecuación de un oscilador harmónico de frecuencia angular ω0 .
√
Usando la notación compleja (i ≡ −1), la solución general es
I(t) = Re(Aeiφ emt ),
(4.110)
donde
m2 + ω02 = 0
m2 = −ω02
√
m = −1ω0 = iω0
, así que
I(t) = Re(Aeiφ emt ) = A cos(ω0 t + φ),
(4.111)
(4.112)
(4.113)
(4.114)
donde A (amplitud real) y φ (fase inicial) son dos constantes reales estacionarias que
satisfacen las dos condiciones iniciales. Integrando con respecto al tiempo tenemos que
Q(t) =
A
sin(ω0 t + φ).
ω0
Vamos ahora a definir las constantes usando
q




A=
I02 + ω02 Q02
I(0) = I0 A cos φ
A
ω0 Q0
−1


Q(0) = Q0
sin φ
 φ = tan
ω0
I0
(4.115)
(4.116)
lo que determina A y φ en función de los valores iniciales Q0 e I0 . Por ejemplo, si
inicialmente I0 = 0, entonces
π A = ω0 Q0
φ=
(4.117)
2
La energía almacenada en el capacitor en un instante t es
UC (t) =
A2
1
Q 2 (t)
=
sin2 (ω0 t + φ) = LA2 sin2 (ω0 t + φ),
2
2C
2
2ω0 C
(4.118)
4.1. Ley de inducción de Faraday
215
y podemos pensar en ella como completamente contenida en el campo eléctrico entre las
placas del condensador. La energía almacenada en el inductor en un instante t es:
UL =
1 2
1
LI (t) = LA2 cos[n2 (ω0 t + φ)]
2
2
(4.119)
~ dentro del inductor. La energía total será:
que es la energía contenida en el campo B
U = UC + UL =
1 2 1 A2
LA =
2
2 ω02 C
(4.120)
y se conserva, dada la ausencia de disipación (R = 0)
Figura 4.21: Gráficas de carga y corriente en función del tiempo.
Para la condición inicial I0 = 0 vemos que la carga con la corriente están desfasadas
en π/2.
4.1.16.1.
Ejemplo
En la figura, el capacitor está inicialmente cargado cuando se abre el interruptor S1
y se cierra el interruptor S2 . Entonces se abre el interruptor S2 , eliminando la batería
4.1. Ley de inducción de Faraday
216
del circuito, y el capacitor permanece cargado. Luego el interruptor S1 se cierra, de modo
que el capacitor queda conectado directamente a las terminales del inductor.
Figura 4.22
(a) Determine la frecuencia de oscilación del circuito.
f=
ω0
1
√
=
= 106 [Hz]
2π
2π LC
(b) Determine la carga y la corriente como funciones del tiempo.
Como I0 = 0 (s), tenemos que
π
y
Q(t) = Q0 sin ω0 t +
2 π
I(t) = ω0 Q0 cos ω0 t +
2
(c) ¿Cuáles son los valores máximos de carga y de corriente en el capacitor y en el
circuito, respectivamente?.
Q0 = C ∆V = 1, 08 · 10−10 [C ]
I0 = ω0 Q0 = 2πf Q0 = 6, 79 · 104 [A]
4.1. Ley de inducción de Faraday
4.1.17.
217
Oscilaciones amortiguadas: Circuito RLC
Consideremos ahora una situación más realista donde tendremos una resistencia R
que siempre existe en un circuito, además de L y C .
Figura 4.23: Circuito RLC en serie.
Usando las reglas de Kirchhoff tenemos
Q
dI
+ RI + L
= 0.
C
dt
(4.121)
Derivando con respecto al tiempo, y dividiendo por L tenemos
d2 I
R dI
1
+
+
I = 0,
2
L dt LC
dt
de modo que
Ï + γİ + ω02 I



ω0



(4.122)
1
=√
LC
donde
(4.123)




 γ
R
1
=
=
L
τ
Reconocemos esta ecuación como una ecuación diferencial de un oscilador harmónico
amortiguado, donde la resistencia actúa como amortiguador. La solución general es
I(t) = Re(Aeiφ ept ),
(4.124)
donde
p2 + γP + ω02 = 0
P± =
(4.125)
q
−γ ± γ 2 − 4ω02
2
=−
γ
±
2
r
γ2
− ω02 .
4
(4.126)
4.1. Ley de inducción de Faraday
218
Amortiguamiento subcrítico
Consideremos el caso en que
r
γ
R
1
L
< ω0 ≡
<√
≡R <2
,
2
2L
C
LC
(4.127)
de donde obtendremos
γ
p± = − ± iω1
2
r
con ω1 ≡
ω02 −
γ2
,
4
(4.128)
donde basta tomar la solución con signo +, ya que tenemos dos constantes
arbitrarias A y φ para satisfacer las condiciones iniciales
γ
γ
I(t) = Re Ae 2 ei(ω1 t+φ) = Ae 2 t cos(ω1 t + φ)
(4.129)
La corriente oscila, pero con amortiguamiento exponencial (envolvente) de constante
de tiempo 2/γ = 2π
Figura 4.24: Carga en función del tiempo para un circuito RLC
amortiguado.
Amortiguamiento débil
Vamos a suponer ahora el caso en que
r
γ
R
1
L
ω0 ≡
√
≡R 2
,
2
2L
C
LC
(4.130)
4.2. Corriente Alterna (AC)
219
de donde obtendremos
p± = −
γ
± iω1
2
con ω1 ≡ ω0 .
(4.131)
En este caso
Z
t
Q(t) =
0
0
Z
iφ pt 0
Re(Ae e ) = Re Ae
I(t )dt =
0
t
pt
iφ ep
,
(4.132)
0
γ
+ iω0 .
2
En el denominador vamos a aproximar P ≈ iω0
iA − γ t i(ω1 t+φ)
A γt
2
Q(t) ≈ Re − e e
≈
e 2 sin(ω1 t + φ).
ω0
ω0
donde p = p+ = −
(4.133)
La energía almacenada en el capacitor en un instante t es
Uc (t) =
Q 2 (t)
A2 −γt 2
LA2 −γ 2
=
e
sin
(ω
t
+
φ)
=
e sin (ω1 t + φ).
1
2C
2
2ω02 C
(4.134)
La energía almacenada en el inductor en un instante t es
UL (t) =
LA2 −γt
LA2 −γ 2
1 2
LI (t) =
e cos2 (ω1 t + φ) =
e sin (ω1 t + φ).
2
2
2
(4.135)
Luego, la energía total almacenada en el circuito en un instante t es
U(t) = Uc (t) + UL (t) =
4.2.
1 2 −γt
LA e .
2
(4.136)
Corriente Alterna (AC)
Corriente alterna ⇒ ν = 60 [ciclos/s]
donde ω = 2πν = 377 [Hz]
Ventaja: Voltaje fácilmente aumentable o disminuible usando transformadores. La
energía eléctrica se transmite en líneas de alto voltaje (corriente baja) para reducir la
pérdida por efecto Joule (P = I 2 R) en los hilos, y se transforma a 220 [V ] al llegar a
destino.
La respuesta del sistema a una corriente alterna es de dos tipos:
4.2. Corriente Alterna (AC)
220
Respuesta Transiente Que mantiene el efecto de las condiciones iniciales y tiende a
desaparecer para t τ, donde τ es una constante de tiempo característica.
La respuesta es la solución de una ecuación diferencial homogénea (sin fuerza
externa), y corresponde a las oscilaciones libres del circuito RLC amortiguadas por
la disipación en la resistencia.
Respuesta Estacionaria Que permanece para t → ∞ y corresponde a las oscilaciones
forzadas, con la misma frecuencia externa que la excitación externa (generador).
Vamos a discutir ahora la solución estacionaria. Como el sistema oscila con la misma
frecuencia ω, es útil el empleo de la notación compleja, cuya dependencia temporal es
de la forma
d
↔ iω.
(4.137)
eiωt →
dt
Vamos a usar la siguiente notación
V (t) = Re[V̂ (t)]
(4.138)
iωt
V̂ (t) = V̄ e
(4.139)
V̄ = Vm eiφ ,
(4.140)
V (t) = Re[Vm ei(ωt+φ) ] = Vm cos(ωt + φ),
(4.141)
de modo que
donde Vm = |V̄ | es el valor máximo de V (t).
Análogamente
4.2.1.
I(t) = Re[Î(t)] = Re[Īeiωt ]
(4.142)
ε(t) = Re[ε̂(t)] = Re[ε̄eiωt ].
(4.143)
Reactancias
En un circuito puramente inductivo tenemos
4.2. Corriente Alterna (AC)
221
Figura 4.25: Bobina de inductances L conectado a un generador de
corriente alterna.
dI
=0
dt
dI
= ε.
L
dt
ε−L
(4.144)
(4.145)
En notación compleja tendremos, tomando en cuenta las ecuaciones (4.138)
L
por otra parte
L
dÎ
= ε̂
dt
ε̂ = ε̄eiωt ,
(4.146)
(4.147)
dÎ
d
= L (Îeiωt ) = iωLÎeiωt
dt
dt
(4.148)
= iωLÎ
ε̄
eiωt
eiωt
(4.149)
entonces
ε̄ = iωLÎ = e
iπ/2
ωLÎ.
Si tomamos que ε̄ = εm implica que ε = Re[εm eiωt ] = εm cos(ωt) entonces
ε̄ i(ωt−π/2)
iωt
e
,
I(t) = Re[Īe ] = Re
ωL
(4.150)
(4.151)
lo que resulta
ε(t) = εm cos(ωt)
εm
I(t) =
sin(ωt).
ωL
(4.152)
(4.153)
4.2. Corriente Alterna (AC)
222
Recordando que LdI/dt dt es también una caída de tensión V a través del inductor,
tenemos entonces
V = Re[V̄ eiωt ]
(4.154)
V̄ = iωLĪ = ωLeiπ/2 Ī
(4.155)
V̄
Ī
= iωL = ωLeiπ/2 ,
(4.156)
de modo que en el inductor, el factor i = eiπ/2 muestra que la corriente en el inductor
esta atrasada π/2 en relación al voltaje
Figura 4.26: Diagrama de fase para un circuito inductivo
En el plano complejo, los vectores V̂ e Î. giran en sentido antihorario con una velocidad
angular ω.
La razón
Vm
= ωL ≡ χL
Im
(4.157)
entre los valores máximos de voltaje y de corriente a través del inductor se llama
reactancia inductiva del inductor. En particular,
χL → 0 para ω → 0 (corriente continua) ⇒ inductor se comporta como corto - circuito.
ω → 0 ⇒ ∞ variaciones rápidas son bloquedas.
Análogamente, si consideramos un circuito puramente capacitivo tendremos
4.2. Corriente Alterna (AC)
223
Figura 4.27: Condensador de capacidad C conectado a un generador
de corriente alterna.
Q
=0
C
Q = CV
ε−
I=
dQ
dV
=C
,
dt
dt
(4.158)
(4.159)
(4.160)
donde tenemos que
Î = Īeiωt = C
dV̂
d
= C (V̄ eiωt ) = iωC V̄ eiωt
dt
dt
⇒ Ī = iωC V̄
⇒
V̄
Ī
=−
1 −iπ/2
i
Ī =
e
,
ωC
ωC
luego la corriente en un capacitor esta adelantada π/2 en relación al voltaje
Figura 4.28: Diagrama de fase para un circuito capacitivo
(4.161)
(4.162)
(4.163)
4.2. Corriente Alterna (AC)
224
La reactancia capacitiva del condensador es
1
Vm
=
≡ χC ,
Im
ωC
(4.164)
en particular
ω → 0, χC → ∞ ⇒ Las placas del condensador están aisladas una de la otra (circuito abierto)
ω → ∞, χC → 0 ⇒ Variaciones rápidas son transmitidas.
4.2.2.
Impedancia
Consideremos ahora un circuito RL
dI
ε − IR − L
=0
dt
dI
V = IR + L
dt
de forma que
d iωt
(Īe )
dt
= (R + iωL)Îeiωt = (R + iωL)Î,
(4.165)
(4.166)
V̂ = V̄ eiωt = R(Îeiωt ) + L
(4.167)
V̂ = V̄ eiωt
(4.168)
V̂
V̄
≡ Z̄ = R + iωL = R + iχL ,
(4.169)
Î
Ī
donde Z̄ se conoce como la impedancia compleja: su parte real es la resistencia R, y su
parte imaginaria es la reactancia inductiva χL = ωL.
=
La relación
V̄ = Z¯I
(4.170)
es una generalización de la Ley de Ohm. Volvamos ahora a la notación real, con V̄ = Vm ,
V (t) = Re[V̂ (t)] = Re[V̄ eiωt ] = Re[Vm eiωt ] = Vm cos(ωt)
" #
Vm eiωt
Vm i(ωt−φL )
V̂
= Re
= Re
e
I(t) = Re[Î(t)] = Re
Z eiφL
Z
Z̄
Vm
Vm
−1 ωL
I(t) =
cos(ωt − φL ) = √
cos ωt − tan
.
Z
R
R 2 + ω 2 L2
(4.171)
(4.172)
(4.173)
La amplitud máxima de corriente es Im = Vm /Z y su fase está atrasada en relación
al voltaje por
−1 ωL
φL = tan
(4.174)
R
4.2. Corriente Alterna (AC)
225
que para R → 0 tiende a π/2 (resultado anterior).
Análogamente, para un circuito RC tenemos
Q
− IR = 0
C
Q̂
= − ÎR
C
Î
dÎ
= iωV̄ = + R
C
dt
1
1
Î,
=
+ iωR Î = iω R +
C
iωC
ε−
(4.175)
V̂
(4.176)
V̂
dt
V̂
dt
(4.177)
(4.178)
de donde tendremos
V̂
Î
V̄
=
Ī
≡ Z̄ = R −
i
= R − iχC ≡ Z e−iφC .
ωC
(4.179)
Volvamos ahora a la notación real, con V̄ = Vm
V (t) = Re[V̂ (t)] = Re[V̄ eiωt ] = Re[Vm eiωt ] = Vm cos(ωt)
"
#
Vm eiωt
V̂ (t)
Vm i(ωt−φC )
= Re
I(t) = Re[Î(t)] = Re
= Re
e
Z eiφC
Z
Z̄
1
Vm
Vm
−1
cos ωt − tan
I(t) =
cos(ωt − φC ) = r
.
Z
ωRC
1
2
R + 2 2
ω C
(4.180)
(4.181)
(4.182)
La fase de la corriente está adelantada en φC con respecto al voltaje. Cuando
R → 0 ⇒ φC → π/2
4.2.3.
Valor eficaz y potencia media
La potencia instantánea disipada en calor por una corriente alterna en una resistencia
R es
dW
2
= [I(t)]2 R = Im
R cos2 (ωt + φ)
(4.183)
dt
donde φ es la fase de la corriente. La potencia oscila periódicamente entre cero y el valor
2 R.
máximo Im
4.2. Corriente Alterna (AC)
226
Figura 4.29: Gráfico de la corriente al cuadrado en una resistencia en
función del tiempo.
En la práctica, estamos interesados en el valor medio de la potencia sobre un periodo
dW
dt
2
= Im
Rhcos2 (ωt + φ)i,
(4.184)
donde los corchetes h i indican el valor medio temporal, definido, para cualquier función
f (t) por
Z
1 t+T 0 0
f (t )dt ,
(4.185)
hf (t)i ≡
T t
de esta manera tenemos que
hcos2 (ωt + φ)i = hsin2 (ωt + φ)i =
E 1
1D 2
cos (ωt + φ) + sin2 (ωt + φ) = ,
2
2
(4.186)
luego
dW
w
= Im
Rhcos2 (ωt + φ)i
dt
1 w
dW
= Im
R ≡ Ie2 R,
dt
2
donde
Im
Ie = √ ∼
= 0, 707Im
2
(4.187)
(4.188)
(4.189)
que se conoce como el valor efectivo o valor eficaz de la corriente. Un resultado análogo
se obtiene para el voltaje
Vm
Ve = √ .
(4.190)
2
Cuando se dice que el voltaje de una linea es de 110 [V ], este es el valor eficaz: el
√
valor máximo correspondiente es de 110 2 ≈ 156 [V ].
4.2. Corriente Alterna (AC)
227
Análogamente, para cualquier circuito de corriente alterna, con una fem que lo
alimenta dada por
ε(t) = V (t) = Vm cos(ωt)
(4.191)
y si la corriente generada en el circuito es
I(t) = Im cos(ωt − φ),
(4.192)
la potencia instantánea en el circuito es
P(t) = ε(t)I(t) = Vm Im cos(ωt) cos(ωt − φ).
(4.193)
Nuevamente, lo que interesa es la potencia media hP(t)i
Como
cos(ωt − φ) = cos(ωt) cos φ + sin(ωt) sin φ,
(4.194)
hP(t)i = Vm Im [cos φhcos(ωt)2 i + sin φhcos φ sin φi],
(4.195)
entonces
de modo que
hP(t)i =
1
Vm Im cos φ
2
(4.196)
donde cos φ se conoce como factor de potencia. Así, por ejemplo, en los circuitos puramente
reactivos (que sólo contienen L o C , sin R), vimos que φ ± π/2, de forma que cos φ = 0 y
hP(t)i. La energía almacenada en el condensador o en la bobina durante una mitad del
ciclo es restituida a la fuente de alimentación durante la otra mitad de ciclo.
Por otro lado, en un circuito puramente resistivo, el voltaje y la corriente están en
fase, es decir, φ = 0. Si R es la resistencia total del circuito
hPi =
1
1 2
1
Vm Im cos φ = Vm Im = Im
R.
2
2
2
Vemos asi una interpretación física y la importancia de la fase φ entre V e I.
(4.197)
4.2. Corriente Alterna (AC)
228
4.2.4.
Resonancia: Circuito RLC
Figura 4.30: Circuito en serie que consiste en un resistor, un inductor
y un condensador conectado a un generador de corriente alterna.
La impedancia de este circuito, con R, L, C en serie es
Z = R + iχL − iχC
1
Z = R + i ωL −
.
ωC
(4.199)
V̂ (t) = Re[V̄ eiωt ] = Re[Vm eiωt ] = Vm cos(ωt)
(4.200)
Z̄ = Z eiφ ,
(4.201)
(4.198)
Si tomamos que
y que
entonces
"
I(t) = Re
V̂
Z̄
#
e
iωt
Vm i(ωt−φ)
Vm
= Re
e
=
cos i(ωt − φ),
Z
Z
(4.202)
de forma que
Im =
Vm
Vm
Vm
=p
=s
2 .
2
2
Z
R + (χL − χC )
1
R 2 + ωL −
ωC
(4.203)
Debido a que la impedancia depende de la frecuencia de la fuente, la corriente en el
circuito RLC también depende de la frecuencia. La frecuencia ω0 a la cual χL − χC = 0
4.2. Corriente Alterna (AC)
229
se conoce como frecuencia de resonancia del circuito
χL = χC
(4.204)
1
ωC
1
⇒ ω2 =
LC
ωL =
(4.205)
(4.206)
1
⇒ ω ≡ ω0 = √ .
LC
(4.207)
Note que esta frecuencia también corresponde a la frecuencia natural de oscilación
de un circuito LC
Vm
Im (ω0 ) =
.
(4.208)
R
Para esta frecuencia la reactancia se anula, y la impedancia equivale a la resistencia
R. Así, la corriente en un circuito RLC alcanza su máximo valor cuando la frecuencia del
voltaje aplicado equivale a la frecuencia natural, que depende sólo de L y C . Además, a
esta frecuencia la corriente está en fase con el voltaje aplicado.
Vamos a estudiar el comportamiento de Im (ω) para ω próximo a ω0 . Para esto, notemos
que
(
2
2 )
ω
1
1
ω
0
R 2 + ωL −
= R2 1 + 2
ω0 L −
(4.209)
ωC
ω0
ωω0 C
R
(
2 )
ω0
ω0 L 2 ω
2
−
=R 1+
(4.210)
R
ω0 ωω02 LC
(
)
ω
1 2
ω0 2
2
2
2
R + ωL −
=R 1+Q
−
,
(4.211)
ωC
ω0
ω
donde Q = ω0 L/R es el factor de calidad de la frecuencia ω0 . Así tenemos que
Vm
Vm
2 = s
2 ,
1
ω
ω
0
R 2 + ωL −
R 1 + Q2
−
ωC
ω0
ω
Im = s
como
Im
→ 0 para
Vm
(
ω → 0
ω → ∞
(4.212)
)
(4.213)
y es máximo para ω = ω0 , entonces tenemos un Peak para ω0 . Para medir el largo de
√
Peak, podemos tomar los valores de ω para los cuales Im cae a 1/ 2 de su valor máximo
4.2. Corriente Alterna (AC)
230
Vm /R, o sea
Im =
Vm
s
R
1
Vm 1
2 = R √2 ,
ω
ω0
1 + Q2
−
ω0
ω
(4.214)
como
ω
ω0 2
Q
−
ω0
ω
ω
ω0
⇒
−
ω0
ω
2
ω − ω02
ωω0
(ω − ω0 )(ω + ω0 )
ωω0
2
=1
1
Q
1
=±
Q
1
=±
Q


ω
1
1  1
ω − ω0
=±
= ±
⇒
ω0 Q ,
ω0
ω + ω0 Q
1+
ω
(4.215)
=±
(4.216)
donde tenemos que


∆ω
1  1 
=±
,
ω0
Q 1 + ω0
ω
donde ∆ω = ω − ω0 es la desviación
(4.217)
En particular, si Q 1 entonces ∆ω/ω0 1
Figura 4.31: Potencia media en función con la frecuencia de un circuito
en serie RLC.
Una aplicación importante de un circuito resonante es como selector de frecuencias.
En un receptor de radio podemos usar este circuito en que C es variable. Cuando la
4.2. Corriente Alterna (AC)
231
frecuencia ω0 definida esta en resonancia con una estación de radio, aparece en el
capacitor un voltaje elevado, para Q elevado, donde las otras estaciones caen fuera del
largo del Peak.
4.2.5.
Transformadores
Un transformador ideal es el ilustrado en la figura, donde las bobinas primaria y
secundaria están enrolladas en torno a un mismo núcleo de hierro.
Figura 4.32: Transformador ideal compuesto de dos bobinas enrolladas
en el mismo núcleo de hierro.
En este caso, el flujo magnético pasa casi completamente a través del hierro,
y entonces, el flujo magnético φ que atraviesa cada espira es (como muy buena
aproximación) el mismo valor en la bobina primaria y secundaria.
Como la bobina primaria tiene N1 espiras y la secundaria N2 , tenemos:
Por la Ley de Mallas (Kirchhoff)
ε1 = N1
dφ
dt
(4.218)
Por la Ley de Inducción (Faraday)
R2 I2 = V2 = −N2
de modo que
V2
N2
=− ,
ε1
N1
dφ
,
dt
(4.219)
(4.220)
4.2. Corriente Alterna (AC)
232
donde el signo sólo indica que la fem inducida se opone a la fem fuente. De manera que
un transformador puede fácilmente aumentar o disminuir el voltaje fuente simplemente
cambiando el número de vueltas de las bobinas.
4.2.5.1.
Ejemplo
Un generador suministra 150 [V ] (efectivos) al devanado primario de un transformador
ideal de 282[vueltas]. El devanado secundario tiene 920[vueltas]. ¿Cuál es el voltaje efectivo
de salida?.
Solución
√
N1
V1m
V1e 2
V
√ = 1e
=
=
N2
V2m
V2e
V2e 2
N2
920
⇒ V2e =
V1e =
(150 [V ]) = 489, 36 [V ]
N1
282
4.2.6.
Filtros
Si consideramos un circuito con C y L, donde ε es la fem asociada a un generador
de corriente alterna, entonces
(4.221)
ε = IZ ,
donde
1
Z̄ = iχL − iχC = i ωL −
ωC
(4.222)
y el voltaje V entre los terminales del capacitor es
Ī
ε
ε
=
=−
1
iωC
iωC Z̄
εC ωL −
ωC
V̄ = IZ c =
⇒ V̄ =
ε
(1 − ω2 LC )
(4.223)
(4.224)
(4.225)
V̄
=
ε
(
1
1−
ω
ω0
2
Vω → 0 = ε
Vω → ∞ = 0
)
(4.226)
El circuito deja pasar señales de baja frecuencia y bloquea señales de alta frecuencia.
4.2. Corriente Alterna (AC)
233
Si intercambiamos los papeles de C y L, Z̄ y Ī no se modifican, pero V aparece ahora
entre los terminales del inductor
V̄ = IZ L = iωLĪ =
⇒ V̄ =
iωLε
Z̄
iωLε
=− 1
i ωL −
ωC
ε
1 − ω2 LC
(4.227)
(4.228)
(4.229)
V̄
=
ε
(
1
1−
ω
ω0
2
Vω → 0 = 0
Vω → ∞ = ε
)
(4.230)
Este circuito deja pasar señales de alta frecuencia y bloquea las de baja frecuencia.
234
4.2. Corriente Alterna (AC)
Ejercicios Propuestos
Inducción Electromagnética.
1. Un solenoide de 2, 5 [cm] de diámetro y 30 [cm] de longitud tiene 300 vueltas y lleva
una intensidad de corriente de 12 [A]. Calcule el flujo a través de la superficie de un
disco de 5 [cm] de radio que está colocado de forma perpendicular y centrado al eje
del solenoide.
2. Una espira circular de alambre de radio R se coloca en un campo magnético uniforme
~ y entonces se impulsa para que gire con una velocidad ω alrededor de un eje a
B
través de su diámetro. Determine el flujo magnético a través de la espira como función
del tiempo si el eje de rotación está:
~
(a) Perpendicular a B.
~
(b) Paralelo a B.
3. Se coloca una espira plana en un campo magnético uniforme cuya dirección es
perpendicular al plano de la espira. Si el área de la espira aumenta a razón de
0, 04 [m2 /s] se induce una fem de 0, 16 [V ], ¿cuál es la magnitud del campo magnético?.
4. Una bobina circular tiene un diámetro de 16, 7 [cm] y 24 vueltas. El campo magnético
es perpendicular al plano de las espiras. Si el campo aumenta linealmente de 2 [µT ] a
8 [µT ] en un tiempo de 0, 6 [s], ¿cuál es la fem inducida?.
5. Un campo magnético uniforme y constante B = 0, 5 [T ] pasa a través de una bobina
plana circular de alambre de 16 vueltas, donde cada una de las espiras tiene un
área de 4, 8 [cm2 ]. Si la bobina gira sobre un eje que pasa por su diámetro con una
236
Ejercicios propuestos Inducción Electromagnética.
velocidad angular ω = 60π [rad/s], calcule la fem inducida como función del tiempo, si
inicialmente en t = 0 [s] el campo magnético es perpendicular al plano de la bobina.
6. Una bobina de N vueltas y área A está situada en el interior de un solenoide
coaxialmente (el eje del solenoide coincide con el de la bobina). El solenoide tiene
n vueltas por metro, y por él circula una corriente variable en el tiempo de acuerdo a
la expresión I = I0 (1 − exp −αt). Calcule la fem inducida en la bobina.
7. Existe un campo magnético a través de una bobina circular de radio R y N vueltas de
alambre; la dirección del campo es perpendicular al plano de la bobina. La magnitud
del campo en el plano de la espira es B = B0 (1 − r/2R) cos(ωt), donde r es medida
desde el centro de la espira. Determine la fem inducida en la espira.
8. Un solenoide largo de radio r y longitud L de N vueltas tiene a su alrededor una espira
de radio R coaxial al solenoide. Con una resistencia variable se hace que la intensidad
de corriente disminuya linealmente de 10 [A] hasta 5, 6 [A] en 1, 5 [s]. Si r = 4, 5 [cm],
L = 2 [m] y N = 4000 vueltas, calcule la fem inducida en la espira circular.
9. Una corriente que varía en el tiempo de acuerdo a la expresión I = 5 exp −0, 4t [A],
donde t está en segundos, circula por un solenoide circular de radio 4 [cm] que tiene
2500 vueltas/metro. Calcule la magnitud del campo eléctrico inducido a una distancia
de 8 [cm] del eje del solenoide en el instante t = 3 [s].
10. Una barra de longitud L se mueve sobre dos rieles con una velocidad constante. Los
rieles están conectados en uno de sus extremos por una resistencia R, como muestra
la figura 4.33, y un campo magnético uniforme de 352 [T ] está dirigido hacia dentro
de la página. Suponiendo que R = 8, 6 [Ω] y L = 120 [cm], ¿con qué velocidad debería
moverse la barra para producir una intensidad de corriente de 0, 5[A] en la resistencia?.
Figura 4.33: (Problema 10).
Ejercicios propuestos Inducción Electromagnética.
237
11. Dos rieles conductores forman un ángulo θ en donde se unen sus extremos. Una barra
conductora en contacto con los rieles y formando un triángulo isósceles con ellos
empieza a moverse en el vértice en el instante t = 0 y se mueve a rapidez contante ν
hacia la derecha, como muestra la figura 4.34. Un campo magnético uniforme B apunta
hacia fuera de la página. Encuentre la fem inducida como función del tiempo.
Figura 4.34: (Problema 11).
12. Una espira rectangular de área A y resistencia R se coloca en una región donde el
campo magnético es perpendicular al plano de la bobina. La magnitud del campo varía
como función del tiempo de acuerdo a la expresión B = B0 exp −t/τ, donde B0 y τ son
constantes positivas. El campo tiene una magnitud de B0 para t ≤ 0.
(a) Encuentre la magnitud y dirección de la intensidad de corriente inducida en la
espira.
(b) Obtenga el valor numérico de la intensidad de corriente para t = 4 [s] cuando
A = 0, 45 [m2 ], R = 0, 4 [Ω], B0 = 659 [mT ] y t = 5 [s].
13. En un campo magnético uniforme B se deja caer una espira rectangular de masa 200[g],
resistencia 1 [Ω] y dimensiones 50 [cm] de base y 2 [m] de altura. Note que las partes
de los lados verticales dentro del campo son de igual longitud. La espira se acelera
hasta alcanzar su velocidad terminal 3 [m/s] (velocidad constante). Calcule la magnitud
de B.
14. Un generador consta de 97 vueltas de alambre formadas en una bobina rectangular de
50 [cm] por 20 [cm], situada por completo dentro de un campo magnético uniforme de
238
Ejercicios propuestos Inducción Electromagnética.
magnitud 3, 5 [mT ]. Calcule el valor máximo de la fem inducida cuando gira la bobina
a razón de 1200 revoluciones por minuto alrededor de un eje perpendicular al campo.
15. Un alambre conductor con una longitud de 60 [m] puede ser enrollado en N vueltas
cuadradas y usado como la armadura de un generador de C A de frecuencia 60 [Hz].
Si se usa un campo magnético de 1, 23 [T ], ¿cuál debe ser la longitud del lado del
cuadrado de la armadura para generar una fem máxima de 155, 56 [V ]?.
16. Un alambre rígido doblado en forma semicircular de radio 4, 4 [cm] gira con una
frecuencia de 120 [Hz], dentro de un campo magnético uniforme de magnitud 2, 5 [T ],
como muestra la figura 4.35. Calcule el valor máximo de la fem inducida en el conductor.
Figura 4.35: (Problema 16).
17. Considere un inductor con núcleo de aire de una longitud de 28 [cm] y 78, 54 [cm2 ] de
área de sección transversal. ¿Cuántas vueltas por metro debe tener el inductor para
tener una inductancia de 77 [µH]?.
18. Una intensidad de corriente de 45 [mA] circula por un solenoide con núcleo de aire de
450 vueltas y 14 [mH]. Calcule el flujo magnético a través del solenoide.
19. Por un solenoide de 1, 53 [mH] pasa una intensidad de corriente que varía con el
tiempo de acuerdo a la expresión I(t) = (2t 3 − 5t 2 + 3t + 6)A, donde t está medido en
segundos.
(a) Calcule la magnitud de la fem inducida en t = 2 [s] y t = 4 [s].
(b) ¿Para qué valor del tiempo la fem será cero?.
Ejercicios propuestos Inducción Electromagnética.
239
20. Tres inductores de 400, 200 y 100 vueltas están conectados en serie y separados por
una gran distancia. Los tres inductores tienen el mismo radio (0, 5 [cm]) y la misma
longitud (6 [cm]). ¿Cuál es la inductancia equivalente de las 700 vueltas cuando los
inductores se conectan en serie?.
21. Dos inductores L1 y L2 están conectados en paralelo y separados por una gran
distancia. Calcule la inductancia equivalente.
22. Un toroide de sección transversal circular, con núcleo de aire, con N vueltas, radio
interior R y radio de la sección transversal r. Si R r, el campo magnético
en el interior del toroide es básicamente igual al de un solenoide muy largo,
el cual ha sido doblado para formar un circulo de radio R. Utilizando el campo
uniforme de un solenoide largo, muestre que la autoinductancia del toroide está dada
(aproximadamente) por L = µ0 N 2 A/2πR.
23. Dos alambres paralelos largos, cada uno de radio a, cuyos centros están separados
por una distancia c, conducen corrientes iguales en dirección contraria. Despreciando
el flujo en los alambres mismo, calcule la inductancia de una longitud l de tal par de
alambres.
24. Un solenoide largo consta de N1 vueltas con un radio R1 . Un segundo solenoide,
con N2 vueltas de radio r2 , tiene la misma longitud que el primero y se encuentra
completamente dentro de este, con sus ejes coincidentes.
(a) Suponiendo que por el solenoide 1 circula una intensidad de corriente I, calcule
la inductancia mutua.
(b) Ahora suponga que por el solenoide 2 circula la misma intensidad de corriente I (y
no circula corriente por el solenoide 1). Calcule la inductancia mutua. ¿Se obtiene
el mismo resultado?.
25. Una intensidad de corriente de 5 [A] circula por un solenoide de 120 vueltas, 7 [cm] de
largo y 1, 5 [cm] de diámetro. Una espira de radio 4 [cm] tiene su centro en el eje del
solenoide; el plano de la espira es perpendicular al eje del solenoide y pasa por el
centro de éste. Calcule la inductancia mutua de los dos, si el plano de la espira pasa
por el centro del solenoide.
26. Dos espiras de alambre circulares con centro común y que están en el mismo plano
tiene radios R y r, con R r.
240
Ejercicios propuestos Inducción Electromagnética.
(a) Encuentre la inductancia mutua.
(b) Calcule la inductancia mutua para r = 1 [cm] y R = 15 [cm].
27. Considere un inductor de núcleo de aire de 5980 vueltas, 8 [mm] de radio y 1, 2 [m] de
longitud. Por el solenoide circula una intensidad de corriente de 3, 43 [A]. Determine
la energía almacenada en el campo magnético.
28. Se tiene un solenoide con núcleo de aire de 1220 vueltas por metro perfectamente
enrollado. Encuentre la densidad de energía magnética cerca del centro si por el
solenoide circula una intensidad de corriente de 5 [A].
29. Un tramo de alambre de cobre recto de diámetro 2, 5 [mm] consume una corriente
de 10 [A], distribuida uniformemente. Calcule la densidad de energía magnética a una
distancia de 5 [cm] del eje del alambre.
30. En un circuito como se muestra en la figura 4.36, con una fem de 36 [V ], L = 5, 98 [H]
y R = 7 [Ω], el interruptor se cierra en t = 0.
(a) Calcule la rapidez con la cual se almacena energía en el inductor después de que
ha transcurrido un tiempo igual a dos veces la constante de tiempo del circuito.
(b) ¿Con qué rapidez se disipa energía en forma de calor por efecto Joule en la resistencia en este tiempo?.
(c) ¿Cual es la energía total almacenada en el inductor en este tiempo?.
Figura 4.36: (Problema 30).
31. Considere el circuito de la figura 4.37 con L = 104 [mH], R = 5, 98 [Ω], ε = 12 [V ].
Ejercicios propuestos Inducción Electromagnética.
241
(a) Si el interruptor se cierra en el punto a (conectando la batería), ¿cuánto tiempo
pasa antes de que la intensidad de corriente alcance los 130 [mA]?.
(b) ¿Cuál es la intensidad de corriente que circula por el inductor 0, 1 [s] después de
que éste se cierra?.
(c) Después de un tiempo considerablemente largo, el interruptor se mueve rápidamente de a a b. ¿Cuánto tiempo debe pasar antes de que la intensidad de corriente
disminuya a 250 [mA]?.
Figura 4.37: (Problema 31).
32. Vamos a usar la figura 4.36 con L = 5 [H], R = 6 [Ω], ε = 12 [V ].
(a) Si en t = 0 se cierra el interruptor, calcule el cociente de la diferencia de potencial a través del resistor a la del inductor cuando la intensidad de corriente en el
circuito es igual a 1, 5 [A].
(b) Calcule el voltaje a través del inductor cuando I = 2 [A].
33. Considere el circuito de la figura 4.38.
(a) ¿Cuál es la intensidad de corriente en el circuito en un tiempo suficientemente
grande después de haber posicionado el interruptor en el punto A?.
242
Ejercicios propuestos Inducción Electromagnética.
(b) Ahora el interruptor se pasa rápido de A a B. Calcule el voltaje a través de cada
resistor y del inductor.
(c) ¿Cuánto tiempo pasará antes de que el voltaje a través del inductor caiga a 12 [V ]?.
Calcule la inductancia.
Figura 4.38: (Problema 33).
34. Un circuito LC en serie, donde C = 5 [µF ], oscila a una frecuencia de 100 [Hz]. Calcule
la inductancia.
35. Un circuito LC en serie, donde L = 119 [mH], C = 12, 5 [µF ], donde el capacitor tiene
una carga inicial de 150 [µC ].
(a) Encuentre la frecuencia (en Hz) de la oscilación resultante.
(b) En el instante t = 1 [ms], encuentre la carga en el capacitor y la intensidad de
corriente en el circuito.
36. En un circuito LC circula una intensidad de corriente que oscila con un periodo T . Si
en t = 0 la carga en el capacitor es máxima, ¿en qué tiempo la energía almacenada
en el campo eléctrico del capacitor será igual a la energía almacenada en el campo
magnético del inductor? (Exprese su respuesta en fracciones de T ).
37. Un inductor de 12, 6 [mH] y un capacitor de 1, 15 [µF ] se conectan en serie con un
resistor. ¿Cuál es el valor máximo del resistor que permitirá al circuito continuar
oscilando?.
38. Considere un circuito RLC en serie que consta de un capacitor de 14, 4 [µF ], conectado
a un inductor de 36 [mH] y a un resistor R. Calcule la frecuencia de las oscilaciones
(en Hz) para los siguientes valores de R:
Ejercicios propuestos Inducción Electromagnética.
243
(a) R = 0 [Ω] (sin amortiguamiento).
(b) R = 20 [Ω] (bajo amortiguamiento).
(c) R = 100 [Ω] (amortiguamiento critico).
(d) R = 200 [Ω] (sobre amortiguamiento).
39. Un inductor tiene una reactancia de 45, 2 [Ω] a 50 [Hz]. ¿Cuál será la corriente Peak si
el inductor se conecta a una fuente de 60 [Hz] que entrega un voltaje de 100 [V ]?.
40. Un inductor de 452 [mH] se conecta a un generador de corriente alterna que tiene un
voltaje Peak de 120 [V ].
(a) ¿Cuál es el valor de la frecuencia del generador para que la reactancia del inductor
sea igual a 38 [Ω]?.
(b) Calcule el valor Peak de la corriente en el circuito a esta frecuencia.
41. La reactancia de un capacitor de 25 [µF ] tiene que ser menor que 377 [Ω].
(a) ¿Cuál es el rango de frecuencias para lograr esto?.
(b) Dentro de este rango de frecuencias, ¿cuál sera la reactancia de un capacitor de
35 [µF ]?.
42. Un circuito de corriente alterna puramente capacitivo con C = 27[µF ], V (t) = Vm sin ωt
con Vm = 91, 3 [V ], f = 100 [Hz], ¿cuál es la intensidad de corriente instantánea en el
circuito a t = 0, 0004 [s]?.
43. Un circuito RLC en serie tiene R = 51, 2 [Ω], L = 980 [mH], C = 1, 93 [µF ] y un
generador con Vm = 313 [V ] que opera a 60 [Hz].
(a) Calcule la reactancia inductiva.
(b) Calcule la reactancia capacitiva.
244
Ejercicios propuestos Inducción Electromagnética.
(c) Calcule la impedancia total del circuito.
(d) Calcule la corriente Peak.
(e) Calcule el ángulo de fase.
44. Un inductor de 19, 3 [mH] y un resistor de 7, 47 [Ω] se conectan en serie a una fuente
de corriente alterna de frecuencia variable. ¿A qué frecuencia el voltaje a través de la
bobina se adelantará a la corriente en 60◦ ?.
45. Un circuito RLC en serie tiene R = 512 [Ω], L = 193 [mH], C = 19, 3 [µF ], con un
generador de corriente alterna a 70 [Hz] que entrega al circuito una corriente Peak de
313 [mA].
(a) Calcule el voltaje Peak requerido Vm.
(b) Determine el ángulo con el cual la corriente en el circuito se adelanta o atrasa
respecto al voltaje aplicado.
46. Un circuito de corriente alterna conectado en serie tiene una resistencia R, un inductor
L, un capacitor C y un generador V (t) = Vm cos(ωt) que opera a una frecuencia ω.
(a) Usando Ley de Kirchhoff, demuestre que la impedancia total del circuito está dada
por
1
.
(4.231)
Z̄ = Z exp iφ = R + i ωL −
ωC
(b) Grafique en el plano complejo la impedancia, especificando R, χL, χC , Z , φ.
(c) Defina el factor de calidad de la frecuencia de resonancia. Demuestre que si
√
tomamos valores de ω para los cuales la corriente máxima cae a 1/ 2 de su
valor máximo, entonces


ω − ω0
1  1 
∆ω
≡
=±
(4.232)
ω0
ω0
Q 1 + ω0
ω
Ejercicios propuestos Inducción Electromagnética.
245
47. Calcule la potencia promedio entregada al circuito RLC en serie descrito en el
problema 43.
48. Un inductor de 17, 2 [mH], un capacitor de 6, 23 [µF ], un resistor de 45, 2 [Ω] y un
generador cuya salida está dada por V (t) = 31, 4 sin(350t) [V ] se colocan en serie.
(a) Encuentre la potencia promedio entregada al circuito por la fuente de poder.
(b) Encuentre la potencia promedio disipada por la resistencia.
49. En un circuito RLC en serie, C = 122 [µF ] y L = 193 [mH]. Calcule su frecuencia de
resonancia.
50. Para sintonizar una estación de radio F M que transmite a 97, 7 [MHz] se utiliza un
circuito RLC en serie. El resistor en este circuito es de 8, 2 [Ω] y el inductor es de
1, 2 [mH]. ¿Qué capacitancia debemos utilizar?.
51. Un resistor de 75 [Ω], un inductor de 120 [mH] y un capacitor de 15 [µF ] se conectan en
serie con un generador de corriente alterna de voltaje máximo 120 [V ] y de frecuencia
variable.
(a) Calcule la frecuencia de resonancia del circuito.
(b) Calcule el factor de calidad del circuito.
52. Un generador suministra 150 [V ] (efectivos) al enrollado primario de un transformador
ideal de 282 vueltas. El enrollado secundario tiene 920 vueltas. ¿Cuál es el voltaje
efectivo de salida?.
53. Considere un transformador ideal con N1 y N2 vueltas en el primario y en el secundario,
respectivamente. Demuestre que un transformador de subida (uno con N2 > N1 ) reduce
la corriente a la salida en un factor N1 /N2 .
54. Un transformador ideal de subida tiene un voltaje a través del secundario de 330 [V ]
(efectivos) cuando el voltaje de entrada es de 100 [V ] (efectivos).
(a) Si la bobina del primario tiene 100 vueltas, ¿cuántas vueltas tiene el secundario?.
(b) Si una resistencia de carga a través del secundario consume una corriente de 10[A],
¿cuál debe ser la corriente en el primario?.
246
Ejercicios propuestos Inducción Electromagnética.
55. En el circuito RC de la figura 4.39 con R = 282 [Ω] y C = 6 [µF ] calcule el cociente
entre Vsalida /Ventrada para:
(a) ω = 30 [rad/s].
(b) ω = 3 × 106 [rad/s].
Figura 4.39: (Problema 55).
56. Considere el circuito de la figura 4.40. Encuentre Vsalida /Ventrada si el voltaje de salida
se toma entre los puntos:
(a) a y b.
(b) b y c.
(c) d y e.
Figura 4.40: (Problema 56).
Ejercicios propuestos Inducción Electromagnética.
247
57. Demuestre que dos filtros RC consecutivos con los mismos valores de R y C como se
muestra en la figura 4.41 entregan la siguiente ganancia:
1
Vsalida
=
Ventrada
1 + (RC ω)2
(4.233)
Figura 4.41: (Problema 57).
58. El fragmento de circuito que se muestra en la figura 4.42 se conoce como divisor de
voltaje.
(a) Si Rload no está conectado al circuito muestre que
R2
Vout = V
R1 + R2
(4.234)
(b) Si R1 = R2 = 10 [kΩ], ¿cuál es el menor valor de Rload que puede ser usado de
manera que el voltaje de salida Vout disminuya menos que un 10 % de su valor sin
Rload ? (Vout es medido con respecto a tierra).
Figura 4.42: (Problema 58).
248
Ejercicios propuestos Inducción Electromagnética.
Capítulo 5
Campos en la Materia
a molécula de agua está polarizada eléctricamente - El átomo de oxígeno atrae más a
los electrones que los átomos de hidrógeno - lo que impone al hielo una estructura de
tipo cristalino (por el juego de atracción y repulsión eléctrica) que tiene menos densidad
que si fuese un sólido amorfo. Si no fuese éste el caso, el hielo se acumularía en el fondo
de los océanos y no en sus superficies.
L
5.1.
Campo eléctrico en la materia
5.1.1.
Dipolo eléctrico
Un dipolo eléctrico es un par de cargas de la misma magnitud y signos opuestos, q y
−q, situadas en puntos diferentes. Así, la carga total del dipolo es cero. Si ~l es el vector
posición de la carga positiva con respecto a la negativa, entonces se define el momento
dipolar eléctrico al vector:
~ = q~l
p
(5.1)
5.1. Campo eléctrico en la materia
250
Figura 5.1: Dipolo eléctrico.
Estamos interesados en calcular el potencial V a distancias mucho mayores que el
brazo l = |~l| del dipolo
q
1
1
V (~r) =
−
(5.2)
4πε0 r 0
r
En el caso donde r l podemos hacer la aproximación r 0 = r − l cos θ, de modo que
1
1
1
l
1 l cos θ
=
1 + cos θ = −
+ ...
(5.3)
≈
0
l
r
r
r
r
r2
r 1 − cos θ
r
Así, el potencial está dado por
q
1
V (~r) =
−
4πε0 r 0
q l cos θ
V (~r) =
4πε0 r 2
1 l cos θ 1
q
=
+
−
4πε0 r
r
r2
~ · r̂
~ · ~r
p cos θ
p
p
=
=
=
,
4πε0 r 2
4πε0 r 2
4πε0 r 3
1
r
(5.4)
(5.5)
~ = (0, 0, p), entonces podemos escribir
como ~r = (x, y, z) y p
V (~r) =
pz
,
4πε0 r 3
(5.6)
~ = −∇V (~r). Como el gradiente es un
además podemos calcular el campo usando E
operador de derivación, entonces
∇(f g) = (∇f )g + f (∇g),
(5.7)
de modo que
∇
z
r3
1
= 3 ∇z + z∇
r
1
r3
=
k̂
3z
k̂
3k̂ · r̂
− 4 r̂ = 3 − 3 r̂
r3
r
r
r
(5.8)
5.1. Campo eléctrico en la materia
251
~ = pk̂, entonces
y como p
~ =−
E
~
p
3(~
p · r̂)
+
r̂.
3
4πε0 r
4πε0 r 3
(5.9)
En particular, para los puntos del plano (x, y) tenemos
~ · r̂ = 0
p
~ y, 0) = −
⇒ E(x,
~
p
.
4πε0 r 3
(5.10)
(5.11)
Por otro lado, para los puntos alineados con el dipolo tenemos r = |z| y r̂ = k̂
~ 0, z) =
E(0,
~
p
,
2πε0 r 3
(5.12)
que tiene el signo opuesto y el doble de magnitud.
5.1.2.
Ejemplos de dipolos en la escala microscópica
En la ausencia de un campo externo, una nube de carga asociada al electrón en un
átomo de hidrógeno está concentrada en el protón (núcleo), y el átomo no tiene momento
dipolar eléctrico permanente.
~ el centro de carga negativo de la nube
Cuando se aplica un campo eléctrico externo E,
~ y aparece un dipolo eléctrico, inducido por
electrónica se mueve en sentido opuesto a E,
el campo eléctrico externo.
Lo mismo ocurre con átomos más complejos y con moléculas no polares (sin momento
dipolar permanente) donde un campo externo produce polarización.
Las moléculas sin centro de simetría pueden tener momentos bipolares permanentes,
los cuales se conocen como moléculas polares.
5.1. Campo eléctrico en la materia
252
Figura 5.2: Molécula de agua h2 o que tiene una polarización
permanente como resultado de su geometría.
5.1.3.
Dipolo en un campo uniforme
~ uniforme, las fuerzas que actúan
Si tenemos un dipolo en un campo eléctrico externo E
sobre sus cargas son
Figura 5.3: Dipolo eléctrico en un campo eléctrico uniforme.
~ = −F~−
F~+ = qE
(5.13)
Este par de fuerzas forma un torque que está dado por
~ =p
~ = pE sin θ
~×E
τ~ = ~l × F~+ = q~l × E
~
que tiende a alinear el dipolo paralelamente a E.
(5.14)
5.1. Campo eléctrico en la materia
5.1.4.
253
Energía potencial
Consideremos ahora la energía potencial del dipolo cuando las cargas están situadas
~ r ) cualquiera.
en los puntos ~r y ~r + ~l de un campo E(~
La energía potencial de una carga q es un punto ~r de un campo electrostático externo
~
E es
U(~r) = qV (~r),
(5.15)
~ Así, la energía potencial de un dipolo en un
donde V (~r) es el potencial asociado a E.
~ cualquiera es
campo externo E
U(~r) = q[V (~r + ~l) − V (~r)].
(5.16)
Vamos a suponer que las dimensiones del dipolo son despreciables, de modo que ~l
puede tratarse como infinitesimal
de manera que
~ (~r),
V (~r + ~l) − V (~r) = ~l · ∇V
(5.17)
~ r)
~ (~r) = −~
U(~r) = q~l · ∇V
p · E(~
(5.18)
y la fuerza resultante sobre el dipolo es
~ r )].
~ r ) = ∇[~
~ p · E(~
F~ = −∇U(~
(5.19)
Podemos comprender ahora porque una peineta atrae pedazos de papel. Por
inducción, la peineta polariza el papel, creando un dipolo que es atraído hacia la región
de campo más intenso en la vecindad de las puntas de la peineta.
5.1.5.
Dieléctricos
Hasta ahora sólo hemos discutido campos eléctricos en el vacío o en la presencia de
~ = 0. ¿Qué ocurre con el campo en la presencia de
conductores, dentro de los cuales E
un material aislante?
Cavendish (1773) y Faraday (1837) descubrieron, independientemente, que la
capacitancia de un condensador aumenta cuando se coloca un aislante entre las placas.
C = κC0
(5.20)
5.1. Campo eléctrico en la materia
254
Sustancia
κ
Ar
1 (atm)
20 (◦ C )
Agua
destilada
20 (◦ C )
Vidrio
Quarzo
Porcelana
Papel
1,00059
80,4
4 a 10
5
6,5 a 7
3,7
Cuadro 5.1: Constantes dieléctricas de varios materiales
¿Por qué razón aumenta C?
Antes de colocar el dieléctrico teníamos que
Q = C0 V =
ε0 A
V,
d
(5.21)
con el dieléctrico, la carga Q de las placas no cambia, pero C0 → C0 κ. Luego, el voltaje
V debe haber caído un factor 1/κ
V0
,
(5.22)
V0 →
κ
de modo que
Q = C V = C0 κ
Z
pero V = −
V0
,
κ
(5.23)
~ · d~l.
E
De este modo, concluimos que el campo dentro del medio es reducido en
~
~ 0 → E0 .
E
κ
(5.24)
En el pequeño intervalo entre el dieléctrico y la placa, el campo aún debe ser
E0 = σ /ε0 , ya que la densidad superficial σ en las placas no ha cambiado. Luego, al
atravesar la superficie del dieléctrico, el campo sufre una discontinuidad
E0
1
κ −1
~
~
n̂12 · (E2 − E2 ) = E0 − E = E0 −
= E0 1 −
=
E0 = (κ − 1)E (5.25)
κ
κ
κ
Tomando una superficie gaussiana cilíndrica, el flujo que entra en la base inferior es
menor que aquél que sale por la base superior. Recordando la Ley de Gauss
I
I
~
~ · n̂ds = Q ,
φ≡
E · d~s =
E
(5.26)
ε0
S
S
5.1. Campo eléctrico en la materia
255
de modo que en nuestro caso en particular
~2 − E
~1 )ds =
n̂12 · (E
dqp
σp ds
=
ε0
ε0
(5.27)
que indica la presencia, sobre la base superior de la lámina, de una densidad superficial
positiva σp dada por
σp = ε0 (E0 − E) = ε0
κ −1
κ
E0 =
κ −1
κ
σ
(5.28)
Figura 5.4: Carga inducida sobre un dieléctrico colocado entre las
placas de un condensador cargado.
Análogamente, en la base inferior de la lámina dieléctrica debe existir una densidad
negativa correspondiente, −σp , para que la lámina, como un todo, sea neutra. Este efecto
es análogo a la inducción electrostática que ocurre en una lámina conductora. En ese caso,
los electrones libres se movían (orientaban), y en el caso de un aislante, los electrones
están ligados y sólo se polarizan.
Cuando aplicamos un campo externo se produce un desplazamiento de las cargas
~ y de las cargas negativas en la
positivas en la dirección del campo eléctrico E,
dirección opuesta. Sin embargo, aún en la escala microscópica, este desplazamiento es
~ aplicados tienen intensidades mucho
extremadamente pequeño, porque los campos E
menores que los campos intra-atómicos.
5.1. Campo eléctrico en la materia
256
En un material con moléculas polares (gas o líquido), el alineamiento en un campo
aplicado también produce una polarización preferencial en la dirección del campo. Un
elemento de superficie d~s = n̂ds dentro del dieléctrico es atravesado por una carga total
dq como consecuencia del desplazamiento.
~ · d~s = P
~ · n̂ds ≡ Pn ds = σp ds
dq = P
(5.29)
~ E
~
donde P//
5.1.6.
Polarización homogénea
Para un elemento de volumen dv totalmente en el interior del dieléctrico, no hay
variación de carga total, ya que la carga que lo atraviesa hacia fuera a través de la base
superior, es compensada por la que entra a través de la base inferior. Sin embargo, esto
no acontece en la superficie del dieléctrico, ya que faltan vecinos de un lado de manera
que no hay compensación.
Figura 5.5: Dieléctrico polarizado, en donde los momentos dipolares
de las moléculas se alinean con el campo eléctrico externo y producen
una superficie con carga negativa inducida y otra con carga positiva
inducida.
dq = Pn ds ≡ σp ds
~
⇒ σp = Pn = n̂ · P.
(5.30)
(5.31)
5.1. Campo eléctrico en la materia
257
Esto explica la aparición de densidades de carga σp , que se conocen como cargas de
polarización.
Consideremos el siguiente cilindro:
Figura 5.6: Aparición de cargas de polarización.
~
d~
p = ẑ(dq)d = ẑσp dsd = Pẑdv = Pdv
p
~ = d~
⇒ P
,
dv
(5.32)
(5.33)
~ es la polarización dieléctrica y representa el momento dipolar por unidad de
donde P
volumen.
~ y el campo eléctrico E?.
~ La
¿Cuál es la relación que existe entre la polarización P
polarización es proporcional al campo y puede escribirse como
~ = χε0 E,
~
P
(5.34)
donde χ es la susceptibilidad dieléctrica, que es una constante numérica característica
del material. Pero habíamos visto que
σP = P = χε0 E = ε0 (κ − 1)E
⇒ κ =1+χ
lo que relaciona la constante dieléctrica con su susceptibilidad.
(5.35)
(5.36)
5.1. Campo eléctrico en la materia
258
5.1.7.
Polarización inhomogénea
Si la polarización varía de un punto a otro dentro del dieléctrico, lo que se conoce
como inhomogéneo, deja de ser verdad que las cargas sólo aparecen en la superficie.
Figura 5.7: Variación de la polarización de un punto a otro dentro del
dieléctrico.
Z
~ · d~s = −
P
∆q = −
Z
∆s
Usando el teorema de Gauss
Z
~ · n̂ds =
P
∆s
tendremos que
~ · n̂ds
P
(5.37)
∆s
Z
~
~ · P)dv
(∇
(5.38)
∆s
Z
~
~ · P)dv
(∇
=
∆q = −
∆s
Z
ρP dv
(5.39)
∆v
lo que equivale a una densidad volumétrica de carga de polarización
~
~ · P.
ρP = −∇
(5.40)
Si además de esto existiesen en el dieléctrico cargas libres de densidad volumétrica
~ es
ρ (por ejemplo, cargas en el aire), la densidad de carga total que genera el campo E
ρT = ρ + ρP ,
(5.41)
5.1. Campo eléctrico en la materia
259
de modo que
~ ~
~ = ρ + ρP = ρ − ∇ · P
~ ·E
∇
ε0
ε0
ε0
~ + P)
~ =∇
~ + ε0 χ E)
~ =∇
~ =∇
~ =∇
~ = ρ,
~ · ε0 (1 + χ)E
~ · ε0 κ E
~ ·D
~ · (ε0 E
~ · (ε0 E
∇
(5.42)
(5.43)
donde hemos definido un nuevo campo (vector desplazamiento eléctrico)
~ = ε0 E
~ +P
~ = ε0 κ E.
~
D
5.1.7.1.
(5.44)
Ejemplo
Consideremos un capacitor de placas paralelas donde la mitad presenta un dieléctrico
(κ > 1), y la otra mitad no (κ = 1). Calcule la capacitancia.
Solución
Las placas metálicas son equipotenciales. Luego su diferencia de potencial V define
un campo uniforme, E = V /d, el mismo en las dos mitades. En la mitad de la placa con
(κ = 1) tenemos que E = σ /ε0 , donde σ es la densidad de superficial de carga (libre). En
la otra mitad tenemos el mismo campo E que resulta de la carga libre y de la polarización.
σp
κσ
= −(κ − 1)E = E − κE = E −
ε0
ε0
σp
κσ
⇒
=E−
ε0
ε0
σp + κσ
⇒ E=
ε0
Así, la carga total de la placa es
Q=
A
A
1
1
1
A
σ + κσ = (κ + 1)σ A = (κ + 1)ε0 AE = (κ + 1)ε0 V
2
2
2
2
2
d
De modo que
C=
Q
1
ε0 A
κC0 C0
= (κ + 1)
=
+
V
2
d
2
2
Lo que es equivalente a la asociación en paralelo de dos capacitores de área A/2, uno
con un dieléctrico y el otro no.
5.2. Magnetismo en la Materia
260
5.1.8.
Energía
La energía almacenada en un capacitor es
U=
1
CV 2
2
donde C = κC0
(5.45)
Es preciso realizar un trabajo mayor para llegar a la misma carga total, porque parte del
trabajo se gasta en polarizar el material dieléctrico, quedando almacenada como energía
interna de las moléculas polarizadas.
5.2.
Magnetismo en la Materia
n el capítulo anterior vimos que ocurre con el campo eléctrico en el interior de un
material dieléctrico. Vimos que el medio dieléctrico queda polarizado y que las
~ se reduzca dentro del medio.
cargas de polarización contribuyen para que E
E
Vamos a estudiar el análogo donde tendremos campos magnéticos en el interior de la
materia. Es importante recordar que no existen cargas magnéticas; las fuentes de campo
magnético son las corrientes.
El uso de la física clásica no indica que no existirán los materiales magnéticos. Es
por ello que una descripción del magnetismo en la escala atómica requiere mecánica
cuántica.
5.2.1.
Corrientes de magnetización
Ampere sugirió que la magnetización de los medios materiales debiera originarse
a partir de corrientes microscópicas. Consideremos una barra cilíndrica uniformemente
magnetizada en la dirección axial. La uniformidad de la distribución de las corrientes
hace que los elementos adyacentes se cancelen de a pares. Sin embargo, esto no ocurre
en la superficie del cilindro, ya que no existen elementos adyacentes exteriores. El efecto
resultante equivale a una corriente superficial, confinada a la superficie del cilindro.
La densidad de corriente superficial se define entonces como
~Jm = di φ̂
dz
(5.46)
5.2. Magnetismo en la Materia
261
Por otro lado, una espira de altura dz recorrida por una intensidad de corriente di
presenta un momento dipolar magnético:
~ = (di)~s = (di)πa2 k̂
dm
~ = |~Jm |(πa2 )dz = |~Jm |dν
|dm|
~
|dm|
⇒ |~Jm | =
dν
(5.47)
(5.48)
(5.49)
~ es, por definición, el momento dipolar magnético por
Por otro lado, la magnetización M
unidad de volumen:
~
~ ≡ dm
(5.50)
M
dν
de modo que
~
|~Jm | = |M|
(5.51)
~ φ̂ = |M|
~ k̂ × ρ̂
⇒ ~Jm = |M|
(5.52)
~ × ρ̂ ≡ M
~ × n̂
⇒ ~Jm = M
(5.53)
donde n̂ es la normal externa a la superficie del cilindro. Concluimos que ~Jm es la densidad
de corriente superficial de magnetización, y el resultado es el análogo a
~ · n̂
σP = P
(5.54)
De la misma forma que una polarización inhomogénea permite la existencia de una
~ =
densidad volumétrica de cargas de polarización, una magnetización inhomogénea M
~ y, z) también permite una densidad volumétrica de corriente de magnetización
M(x,
~
~ ×M
~jm = ∇
(5.55)
Análogo a la densidad volumétrica de cargas
~
~ ·P
σP = −∇
(5.56)
para un dieléctrico con polarización inhomogénea. Las corrientes ~jm también están ligadas
a los átomos.
En particular, un cilindro largo con magnetización homogénea equivale a una
distribución de corriente superficial
~jm = di φ̂ = M φ̂
dz
(5.57)
Como si fuera un solenoide con espiras muy juntas. Además, la unidad de magnetización
es A/m [Ampere/metro].
5.2. Magnetismo en la Materia
262
5.2.2.
~
El campo B
En la presencia de magnetización, la Ley de Ampere queda como:
~ = µ0 (~j + ~jm ) = µ0~j + µ0 ∇
~
~ ×B
~ ×M
∇
~ − µ0 ∇
~ = µ0~j
~ ×B
~ ×M
⇒ ∇
!
~
~ = ~j
~ × B −M
⇒ ∇
µ0
(5.58)
(5.59)
(5.60)
~ = ~j
~ ×H
⇒ ∇
(5.61)
~ dado por
donde hemos definido un nuevo campo H
~
~ ≡ B −M
~
H
µ0
~ 0 (H
~ + M)
~
⇒ Bµ
(5.62)
(5.63)
Estos resultados son análogos a los dieléctricos, donde
~ =ρ
~ ·D
∇
(5.64)
~ = ε0 E
~ +P
~
D
(5.65)
~ son las mismas que las de la magnetización M,
~ es decir, A/m. Tenemos,
Las unidades de H
por otro lado, que
!
~
B
~ =∇
~ = 1∇
~ −∇
~
~ ·H
~ ·
~ ·B
~ ·M
∇
−M
(5.66)
µ0
µ0
~ = −∇
~
~ ·H
~ ·M
⇒ ∇
5.2.3.
(5.67)
Ecuación constitutiva
Para medios dieléctricos lineales, homogéneos e isotrópicos tenemos la siguiente
relación constitutiva,
~ = ε0 χ E
~
P
(5.68)
~ = ε0 E
~ +P
~ = ε0 (1 + χ)E
~ = ε0 κ E
~ = εE
~
⇒ D
(5.69)
donde κ es la constante dieléctrica, ε es la permitividad del dieléctrico y χ es la
susceptibilidad dieléctrica. Análogamente, si tuviésemos un medio magnético lineal,
5.2. Magnetismo en la Materia
263
~ es proporcional al campo B
~ ó H
~ en el
homogéneo e isotrópico, la magnetización M
interior del medio:
~
~ = χm H
M
(5.70)
~ ≡ µH
~
~ = µ0 (H
~ + M)
~ = µ0 (1 + χm )H
~ = µ0 κm H
B
(5.71)
de modo que
donde κm es la permeabilidad magnética relativa, µ es la permeabilidad magnética del
medio y µ0 es la permeabilidad magnética del vacío.
Unidades:
N
Wb
= 2
A·m
m
N
[µ] = 2
A
A
[H] =
m
A
[M] =
m
[B] =
(5.72)
(5.73)
(5.74)
(5.75)
Los materiales magnéticos lineales son de dos tipos, diamagnéticos µ < µ0 , χm < 0 y
paramagnéticos µ > µ0 , χm > 0. En ambos casos tenemos que |χm | 1, lo que significa
que
µ ≈ µ0 ⇒ B ≈ µ0 H
(5.76)
Efectos más intensos se obtienen en materiales ferromagnéticos, que son no lineales, lo
~
que equivale a decir que χm y µ varían con el campo B.
5.2.4.
La razón giromagnética
Las corrientes microscópicas postuladas por Ampere son corrientes en la escala
atómica. A pesar de que no existe un átomo clásico, podemos considerar un modelo
híbrido, el átomo de Bohr.
5.2. Magnetismo en la Materia
264
Figura 5.8: Electron moviéndose en una orbita circular de radio r,
momento angular L y momento magnético µ.
Si τ es el periodo de la orbita, la intensidad de corriente asociada al movimiento de
la partícula es
q
(5.77)
i=
τ
y el momento dipolar magnético asociado a la órbita es
I
1
~ = i~s = i
~r × d~r
m
(5.78)
2 C
I
~r × d~r = 2~s.
donde
C
Como d~r = ν~ dt (donde ν~ es la velocidad instantánea de la carga),
I
q
~ =
~r × ν~ dt
m
2τ C
(5.79)
~ = M ν~ es el momento lineal, y entonces
Pero si M es la masa de la partícula, p
~r × ν~ =
~
1
~= l
~r × P
M
M
(5.80)
donde ~l es el momento angular de la carga en relación al centro, el que se conserva por
tratarse de un movimiento sobre la acción de fuerzas centrales.
I
q ~1
~ =
m
l
dt
(5.81)
2M τ C
I
pero
dt = τ es el periodo de la orbita.
C
5.2. Magnetismo en la Materia
265
Finalmente tendremos que
q
~ = γ~l ⇒ γ =
m
(razón giromagnética clásica)
2M
e
⇒ γe = −
2Me
(5.82)
(5.83)
~
~ y ~l son aditivos, la misma relación se aplica al momento magnético total M
Como m
asociado a las órbitas de los diferentes electrones del átomo:
~ = γe L~
M
(5.84)
donde L~ es el momento angular orbital resultante de un conjunto de electrones. Sin
embargo, experimentos realizados sobre materiales ferromagnéticos encontraron que
γ = 2γe = −
e
me
(5.85)
O sea, la razón giromagnética experimental es el doble de la razón giromagnética clásica.
El descubrimiento del espín del electrón dio una explicación a este resultado. Además
del momento angular orbital que dice relación con el núcleo atómico, el electrón tiene
un momento angular intrínseco, el espín.
El momento angular total ~J de los electrones de un átomo es la suma de sus momentos
angulares orbitales y de espín,
e ~
~ = gγe~J = −q
m
J
2me
(5.86)
donde g es el factor de Landée, y puede ser calculado con ayuda de la mecánica cuántica
(para el espín de un electrón aislado, (g = 2).
En materiales diamagnéticos, ~J = 0, de manera que los átomos no poseen momento
dipolar magnético permanente (intrínsico). El momento es inducido por el campo externo.
Por su parte, los materiales paramagnéticos tienen ~J 6= 0, por lo que presentan momento
~ es orientar esos momentos.
magnético intrínseco, y el efecto principal del campo B
5.2.5.
Diamagnetismo
Veremos que acontece con el movimiento de los electrones en un átomo cuando es
~ Vamos a suponer un campo de la forma
sometido a un campo externo B.
~ = B(t)k̂
B
(5.87)
5.2. Magnetismo en la Materia
266
Figura 5.9: Movimiento de un electron cuando es sometido a un campo
~
externo B
Por la Ley de Inducción de Faraday tenemos que
I
~ · d~l = − dφ = − d
E
dt
dt
C
dB(t)
2πρhEφ i = −πρ2
dt
ρ dB(t)
hEφ i = −
2 dt
Z
~ · dA
~ = −A dB
B
dt
(5.88)
(5.89)
(5.90)
~ a lo largo de la curva
donde hEφ i es el valor medio de la componente tangencial de E
C . El torque correspondiente sobre el electrón, con relación al centro O, es
hτz i = (−e)hEφ iρ =
1 2 dB
ρ e
2
dt
(5.91)
y por la Ley Fundamental de la Dinámica de las Rotaciones, este torque corresponde a
la tasa media de variación temporal del momento angular orbital lz
dl
dt
=
1 2 dB
ρ e
2
dt
(5.92)
Integrando como función del tiempo tenemos
~
~l1 = 1 ρ2 eB;
2
~ = bk̂, ρ2 = x 2 + y2 )
(B
(5.93)
de modo que el momento magnético dipolar asociado es
e ~
e2 2 ~
~ 1 = γe~l1 = −
m
l1 = −
ρ B
2me
4me
(5.94)
5.2. Magnetismo en la Materia
267
Para un átomo con Z electrones (Z = número atómico), tenemos que sumar sobre todos
ellos, sustituyendo ρ2 por su valor medio. Esperamos que el átomo tenga simetría esférica
en la ausencia de un campo externo, de modo que
hx 2 i = hy2 i = hz 2 i =
1 2
hr i
3
r 2 = x 2 + y2 + z 2
hρ2 i = hx 2 + y2 i =
(5.95)
(5.96)
2 2
hr i
3
(5.97)
y entonces,
~1 = −
m
Z e2 2 ~
hr iB
6me
(5.98)
~ es el momento magnético total del átomo inducido por el campo. Vemos que m
~
donde m
~
~
es antiparalelo a B, en conformidad con la Ley de Lenz. La magnetización M (momento
~ por el número N de átomos
magnético por unidad de volumen) se obtiene multiplicando m
por unidad de volumen.
Ze 2 ~
~ = Nm
~ = −N
M
hr iB
6me
2
(5.99)
~ = χm H
~ yB
~ = µ0 (H
~ + M)
~ tenemos que
Como M
~ = µ0 (1 + χm )H
~ = µH
~
B
(5.100)
~ ≈ µ0 H.
~ De este modo
pero como χm 1 entonces B
~
~ = −µ0 N Z e hr 2 iH
M
6me
Z e2 2
hr i
χm = −µ0 N
6me
2
(5.101)
Fórmula de Langevin
Algunos ejemplos de materiales diamagnéticos son dados en la tabla siguiente:
(5.102)
5.2. Magnetismo en la Materia
268
Materiales
Diamagnéticos
χ
Materiales
Paramagnética
χ
Bismuto
−1, 66 · 10−5
Aluminio
2, 3 · 10−5
cobre
−9, 8 · 10−6
Calcio
1, 9 · 10−5
Diamante
−2, 2 · 10−5
Cloro
2, 7 · 10−4
Oro
−3, 6 · 10−5
Litio
2, 1 · 10−5
Plomo
−1, 7 · 10−5
Magnesio
1, 2 · 10−5
Mercurio
−2, 9 · 10−5
Niobio
2, 6 · 10−4
Nitrógeno
−5, 0 · 10−9
Oxígeno
2, 1 · 10−6
Plata
−2, 6 · 10−5
Platino
2, 9 · 10−4
Silicona
−4, 2 · 10−6
Tungsteno
6, 8 · 10−5
Cuadro 5.2: Susceptibilidades magnéticas para algunas sustancias
diamagnéticas y paramagnéticas a 300 K
5.2.6.
Paramagnetismo
Consideremos una sustancia paramagnética, cuyos átomos o moléculas tienen un
~ 0 |. En la ausencia de un campo magnético externo, los
momento magnético intrínseco |m
~ 0 están orientados aleatoriamente, y la magnetización resultante (valor medio)
dipolos m
es cero.
~ externo tiende a alinear los dipolos, obteniendo una magnetización
Un campo B
~ 6= 0. En este caso, U = −m
~ de modo que se favorecen energéticamente
~ 0 · B,
M
~ de forma que la
orientaciones paralelas de los dipolos con respecto al campo B,
susceptibilidad magnética es χm > 0.
La probabilidad de encontrar una partícula (átomo ó molécula) con energía potencial
U en un campo de fuerzas, a temperatura T , es proporcional al factor de Boltzmann,
= = expU/kB T
(5.103)
donde kB = 1, 38 · 10−23 [J/K ] es la constante de Boltzmann. Para un dipolo magnético
~ la energía potencial es
~ 0 en un campo externo B,
m
~ = −m0 B cos θ
~0 · B
U = −m
(5.104)
5.2. Magnetismo en la Materia
269
~
~ 0 en un campo externo B.
Figura 5.10: dipolo magnético m
Luego, = = expU/kB T = expm0 B cos θ/kB T . El número de partículas por unidad de volumen
~ 0 cae dentro de un ángulo sólido dΩ = sin θdθdφ (coordenadas
en que la dirección de m
esféricas) es
m0 B
cos θ
dn = A=dΩ = A exp kB T
sin θdθdφ
(5.105)
Z
donde A es una constante tal que dn = n es el número total de partículas por unidad
de volumen
Z
A
2π
0
Z
dφ
π
= sin θdθ = n
(5.106)
0
Para los valores usuales de B y T , la energía magnética es mucho menor que la energía
térmica,
m0 B
1
(5.107)
kB T
de modo que
m0 B
cos θ
m0 B
= = exp kB T
≈1+
cos θ + . . .
(5.108)
kB T
de este modo
Z π
m0 B
n = 2πA
1+
cos θ sin θdθ = 4πA
(5.109)
kB T
0
n
⇒ A=
(5.110)
4π
o sea que
n
dn =
4π
m0 B
1+
cos θ sin θdθdφ
kB T
(5.111)
~ basta con considerar
Para calcular la contribución de los átomos a la magnetización M,
~ m0 cos θ, ya que las componentes perpendicular al
la componente en la dirección de B,
5.2. Magnetismo en la Materia
270
campo se cancelan. De esta forma,
Z
Z π
nm0 2π
m0 B
M ≡ m0 cos θdn =
dφ
1+
cos θ cos θ sin θdθ
4π 0
kB T
0
Z
nm20 B π
cos2 θ sin θdθ
M=
2kB T 0
nm20
M=
B
3kB T
Z
(5.112)
(5.113)
(5.114)
Si nuevamente usamos que B ≈ µ0 H, entonces
χm =
nµ0 m20
C
=
3kB T
T
(5.115)
donde C es la constante de Curie. Para algunos ejemplos de materiales paramagnéticos,
dirigirse a la tabla anterior.
5.2.7.
Ferromagnetismo
Las sustancias ferromagnéticas más importantes son el hierro (Fe), níquel (Ni) y el
cobalto (Co)
(a)
(b)
Figura 5.11: Curvas de histéresis.
5.2. Magnetismo en la Materia
271
La figura anterior muestra la curva de histéresis para (a) un material ferromagnético
duro y (b) un material ferromagnético suave.
~ es varios órdenes de magnitud
En un material ferromagnético, la magnetización M
~ versus H
~ es
mayor que en materiales diamagnéticos o paramagnéticos, y la relación M
no lineal. La razón χm = dM/dH define una susceptibilidad entre 102 y 103 .
Figura 5.12: Curva de histéresis para un material ferromagnético.
El punto a corresponde a la magnetización de saturación Ms . El punto b corresponde
a la magnetización remanente Mr , y el punto c corresponde al campo coercitivo o
coercividad, Hc . Como la curva de magnetización depende de la historia, se conoce como
ciclo de histéresis.
Los resultados descritos son válidos para temperaturas menores que una temperatura
característica TC urie del material, conocida como punto de Curie.
5.2. Magnetismo en la Materia
272
Figura 5.13: Magnetización en función de la temperatura absoluta para
una sustancia ferromagnética.
Fe → TC urie = 1043 (K )
(5.116)
Co → TC urie = 1388 (K )
(5.117)
Ni → TC urie = 627 (K )
(5.118)
para T > TC urie , el material se vuelve paramagnético, y su susceptibilidad magnética χm ,
obedece la Ley de Curie-Weiss
χm =
C
,
T − TC urie
T > TC urie
(5.119)
~ ef f que actúa sobre el átomo debe
Pierre Weiss en 1907 propuso que el campo efectivo H
considerar la interacción con los momentos magnéticos de los otros átomos
~ ef f = H
~ + WM
~
H
(5.120)
Aplicando la Ley de Curie (T > TC urie ) tenemos
C~
C ~
~
Hef f = (H
+ W M)
T
T
C~
H
T
C
~
~ =
⇒ M
H,
TC urie = C W
T − TC urie
~ =
M
CW
~
M 1−
=
T
(5.121)
(5.122)
Ley de Curie-Weiss
(5.123)
La naturaleza del campo interno W sólo fue clarificada por la Teoría Cuántica: su
explicación fue propuesta en 1927 por Heisenberg. El ferromagnetismo se origina en
5.2. Magnetismo en la Materia
273
el traslape de las funciones de onda de los electrones. (espín) Como conclusión tenemos
que:
T < TC urie → dipolos alineados
(5.124)
T > TC urie → dipolos desordenados
(5.125)
¿Como se explica entonces que el hierro (TC urie = 1388 K ) esté desmagnetizado a
~ externo para magnetizarlo?.
temperatura ambiente, y se tenga que aplicar un campo B
5.2.8.
Los dominios de Weiss
Una muestra macroscópica de hierro está formada de numerosos microcristales; la
estructura cristalina es cúbica, pero los ejes de los microcristales están orientados
aleatoriamente. La anisotropía de un monocristal implica que existen direcciones
~ las direcciones de fácil
preferenciales de orientación para la magnetización M,
magnetización.
Pierre Weiss postuló en 1907 la existencia de dominios, cada uno de los cuales está
orientado (T < TC urie ) en una dirección de fácil magnetización.
Figura 5.14: Momentos magnéticos polares orientados a al azar en
una sustancia no magnetizada y alineados con el campo magnetizando
la muestra.
Los dominios se forman para reducir su energía en las superficies, pero aumentan su
energía debido a la formación de paredes de Bloch.
paramagnetico
5.2. Magnetismo en la Materia
274
5.2.9.
Circuitos magnéticos
Entre las aplicaciones más importantes del ferromagnetismo, se destaca el uso de
núcleos de materiales ferromagnéticos en bobinas y transformadores, y la aplicación en
electroimanes e imanes permanentes.
Consideremos una bobina toroidal enrollada sobre un núcleo ferromagnético, recorrida
por una corriente i. (Anillo de Rowland)
Figura 5.15: bobina toroidal utilizada para medir las propiedades
magnéticas de un material. El núcleo se hace del material en estudio.
~ las únicas fuentes son corrientes libres, de modo que
Como vimos para H,
~ = ~J
~ ×H
∇
(5.126)
~ · d~l = I
H
(5.127)
2πrH = Ni
(5.128)
~ = Ni φ̂
⇒ H
2πr
(5.129)
I
⇒
C
~ a través de las N espiras es
Por otro lado, el flujo del campo B
Z
~ · d~s = NBS,
φ=N B
(5.130)
5.2. Magnetismo en la Materia
275
~ = µ H,
~ de modo que
pero B
N 2S
i,
2πr
pero l ≡ 2πr es la densidad de vueltas en un toroide, de modo que
φ = NµHS = µ
φ=µ
N 2S
i,
l
(5.131)
(5.132)
Como φ = Li, donde L es la autoinductancia de la bobina, entonces
L
µ
= ,
L0
µ0
(5.133)
donde L0 es la autoinductancia para una bobina sin núcleo de hierro. Así, el núcleo
ferromagnético aumenta la inductancia L, lo que permite reducir las dimensiones de la
bobina y la cantidad de hilos necesarios (disminuyendo la pérdida ohmica). Si i está
variando con el tiempo, entonces
ε=−
dB
dφ
= −NS
.
dt
dt
(5.134)
La potencia necesaria para producir esa variación temporal de la corriente i es
dB
Ni dB
dU
= −εi = NSi
=
sl
,
dt
dt
l
dt
(5.135)
donde l = 2πr, ν = Sl y H = Ni/l entonces
dU = (HdB)ν,
(5.136)
así la variación de densidad de energía µm es
~ · dB.
~
dµm = H
(5.137)
~ = µ0 H,
~ de modo que
En el vacío, B
1 ~
~
B · dB
µ0
B2
⇒ µm =
.
2µ0
dµm =
Volvamos ahora a la expresión del flujo, donde
I
~ · d~l = M Fuerza Magnetomotriz.
Ni = 2πrH =
H
C
(5.138)
(5.139)
(5.140)
5.2. Magnetismo en la Materia
276
~ a través de una espira es
Habíamos visto que el flujo de B
Z
φ = Nφ1 = N
2
~ · d~s = µ N S i
B
l
S
φ1 = µ M
l
(5.141)
(5.142)
y definidos, tenemos entonces que
M = <φ1
con < =
1
µS
Reluctncia.
(5.143)
Ejercicios Propuestos
Campos en la materia.
1. Un dipolo eléctrico es un par de cargas de la misma magnitud y signos opuestos,
situadas en puntos diferentes. Así, la carga total del dipolo es cero.
(a) Demuestre que el potencial eléctrico medido a distancias mucho mayores que el
brazo l está dado por:
~ · ~r
p
(5.144)
V (~r) = k 3
r
(b) Demuestre, usando el gradiente, que el campo eléctrico está dado por:
~
(~
p · ~r)
~ r ) = −k p
+ 3k 3 r̂
E(~
2
r
r
(5.145)
(c) Suponiendo que las dimensiones del dipolo son despreciables, demuestre que la
energía potencial puede escribirse como
~ r)
U(~r) = −~
p · E(~
(5.146)
2. Un dipolo eléctrico está formado por dos cargas de igual magnitud, pero de signo
contrario, separadas por una distancia 2a. Determine el campo eléctrico en el punto
P debido al dipolo eléctrico mostrado en la figura 5.16.
Ejercicios propuestos campos en la materia.
278
Figura 5.16: (Problema 02).
3. Suponga que una molécula de agua (H2 O) tiene un momento bipolar eléctrico igual
~ = 6, 3 × 10−30 (ı̂ + ̂) [C m]. Si colocamos la molécula en la presencia de un
dado por P
~ = 2, 5 × 105 ı̂ [N/C ], encuentre:
campo eléctrico dado por E
(a) El torque ejercido sobre la molécula de agua,
(b) La energía potencial,
(c) La fuerza resultante sobre el dipolo.
4. Suponga un dieléctrico como el de la figura 5.17, el que está polarizado uniformemente
~ Encuentre la densidad superficial de polarización sobre las caras
con polarización P.
1, 2 y 3.
Figura 5.17: (Problema 04).
~ y, z) = (5x 2 + z)ı̂ + 20y̂ − 10k̂.
5. Suponga una polarización inhomogénea dada por P(x,
Ejercicios propuestos campos en la materia.
279
Calcule la densidad volumétrica de carga de polarización ρP (x, y, z). Evalúe en el punto
(x, y, z) = (2, 0, 3).
6. A un capacitor de placas paralelas se le introduce una placa conductora de espesor
s y área A, si las placas del capacitor tienen la misma área A y una separación d
entre ellas, como se muestra en la figura 5.18. ¿Cuál es el valor de la capacitancia del
sistema?.
Figura 5.18: (Problema 06).
7. Un capacitor con placas paralelas cuya área es 200 [cm2 ] tiene un relleno de caucho
(neopreno con κ = 6, 7 y Emax = 13 × 106 [V /m]) que tiene 12 [mm] de espesor.
(a) Calcule la capacitancia.
(b) Calcule el voltaje máximo.
8. Un capacitor tiene placas paralelas cuya área es 0, 12 [cm2 ]. Cuando las placas están
en el aire, la capacitancia es de 16 [pF ].
(a) Calcule el valor de la capacitancia si el espacio entre las placas se llena con mica
de rubí (κ = 5, 4 y la rigidez dieléctrica es Emax = 160 × 106 [V /m]).
(b) ¿Cuál es la máxima diferencia de potencial que se puede aplicar a las placas sin
causar la ruptura eléctrica? (sin dieléctrico).
9. Un capacitor cilíndrico relleno de teflón (κ = 2, 1) tiene una capacitancia por unidad
de longitud de 60 [pF /m]. Si el diámetro interior del conductor exterior es de 2 [cm],
¿cuál es el diámetro del conductor interior?.
10. Un capacitor de placas paralelas y dieléctrico de aire (κ = 1, 0 y la rigidez dieléctrica
es Emax = 3 × 106 [V /m]) puede almacenar una energía máxima Ua. ¿Cuál es la
máxima energía que puede almacenar el capacitor si el espacio se llena con vidrio
pyrex (κ = 5, 6 y la rigidez dieléctrica es Emax = 14 × 106 [V /m])?.
Ejercicios propuestos campos en la materia.
280
11. Un capacitor con placas paralelas y dieléctrico de aire (κ = 1, 0 y la rigidez dieléctrica
es Emax = 3 × 106 [V /m]) se puede cargar hasta Q0 sin que ocurra una descarga
eléctrica. Al introducir una placa de vidrio pyrex (κ = 5, 6 y la rigidez dieléctrica es
Emax = 14 × 106 [V /m]), la carga máxima es Q sin que ocurra una descarga. ¿Cuál es
la razón Q/Q0 ?.
12. Un capacitor con placas paralelas se llena con dos materiales dieléctricos diferentes
del mismo espesor, como se ilustra en la figura 5.19. Calcular su capacitancia.
Figura 5.19: (Problema 12).
13. A un capacitor con placas paralelas, de separación d y capacitancia C0 , se le introduce
una placa dieléctrica de espesor s(s < d). Encuentre la expresión de la nueva
capacitancia. Evalúe la expresión para d = 0, 5 [mm], C0 = 16 [pF ], κ = 6, 9 y
s = 0, 2 [mm].
14. Un condensador de placas paralelas es construido usando un dieléctrico cuya
constante varía con la posición. Las placas tienen un área A. La placa inferior está
en y = 0 y la placa superior está en y = y0. La constante dieléctrica es una función
de la posición y de acuerdo a
3
y
(5.147)
κ =1+
y0
(a) ¿Cuál es la capacitancia?
(b) Use la ley de Gauss para encontrar la densidad de carga volumétrica inducida
ρ(y) dentro del dieléctrico.
15. Determine la fuerza con que se repelen dos cargas positivas puntuales q1 y q2 que se
encuentran sumergidas en el interior de un dieléctrico de permitividad ε.
Ejercicios propuestos campos en la materia.
281
16. Consideremos un ión esférico de carga Q sumergido en un líquido dieléctrico lineal,
homogéneo e isotrópico, siendo ε la permitividad del medio. Calcule el valor del campo
eléctrico a una distancia r del centro del ión.
17. Considerando el átomo de Bohr, demuestre que le momento magnético está dado por
~ = γ~ , donde γ es la razón giromagnética clásica.
m
18. Defina materiales diamagnéticos, paramagnéticos y ferromagnéticos. Identifique
algunos ejemplos para cada tipo de material, diferencias con respecto a los otros
y grafique esquemáticamente magnetización versus campo.
19. Identifique en la curva de histéresis de un material ferromagnético:
(a) La magnetización de saturación.
(b) La magnetización remanente.
(c) El campo coercitivo o coercividad.
(d) Comente que significa cada uno de los valores identificados.
20. Un imán está constituido por una barra cilíndrica de 15 [cm] de largo. Podemos
obtener un solenoide equivalente enrollando sobre un cilindro de cartón, de las mismas
dimensiones, 150 espiras y haciendo pasar por ellas una intensidad de corriente de
3 [A]. Determine la magnetización M del imán.
21. Por un hilo conductor recto y muy largo circula una corriente de 10 [A]. Calcule la
inducción magnética B, la intensidad del campo magnético H y la magnetización M
en un punto que se encuentra a 20 [cm] de él, según se encuentre sumergido:
(a) En el vacío.
(b) En un medio con permeabilidad magnética m.
22. Un anillo de Rowland de 8 [cm] de radio medio está constituido por un enrollado de
800 vueltas de un hilo conductor sobre un núcleo de permeabilidad relativa 1000. Si
se hace pasar una corriente de 5 [A],
(a) Calcule el valor de la inducción magnética B en su interior.
(b) Calcule el valor de la intensidad de campo magnético H en su interior.
(c) Calcule la magnetización M del anillo.
282
Ejercicios propuestos campos en la materia.
Capítulo 6
Ecuaciones de Maxwell
as ecuaciones de Maxwell son un conjunto de cuatro ecuaciones que describen por
completo los fenómenos electromagnéticos. La gran contribución de James Clerk
Maxwell fue reunir en estas ecuaciones largos años de resultados experimentales, debidos
a Coulomb, Gauss, Ampere, Faraday y otros, introduciendo los conceptos de campo y
corriente de desplazamiento, y unificando los campos eléctricos y magnéticos en un solo
concepto: el campo electromagnético.
L
6.1.
Ecuaciones de Maxwell
6.1.1.
Revisión de las leyes generales
Todos los fenómenos electromagnéticos descritos hasta aquí son parte de un
conjunto de ecuaciones básicas que definen el campo electromagnético. Vimos que estas
ecuaciones pueden ser formuladas en forma integral y en forma diferencial usando análisis
vectorial.
Teorema de la divergencia
I
S
~ · d~s =
A
Z
~
~ · Adν
∇
(6.1)
~ · n̂ds
~ ×A
∇
(6.2)
V
Teorema del rotacional
I
C
~ · d~l =
A
Z
S
6.1. Ecuaciones de Maxwell
284
Las ecuaciones básicas para campos electromagnéticos en el vacío son:
Ley de Gauss
I
~ · d~s = q
E
ε0
Z
Z S
1
~
~
ρdν
∇ · Edν =
ε0 V
V
~= ρ
~ ·E
⇒ ∇
ε0
(6.3)
(6.4)
(6.5)
Ausencia de monopolos magnéticos
I
~ · d~s = 0
B
(6.6)
~
~ · Bdν
∇
=0
(6.7)
~ =0
~ ·B
⇒ ∇
(6.8)
S
Z
V
Ley de Ampere
I
~ · d~l = µ0 I
B
Z
Z
~
~
∇ × B · n̂ds = µ0 ~J · n̂ds
C
S
s
~ = µ0~J
~ ×B
→ ∇
(6.9)
(6.10)
(6.11)
Ley de inducción de Faraday
Z
d
~ · n̂ds
~
~
B
E · dl = −
dt s
C
Z
Z ~
∂B
~
~
∇ × E · n̂ds = −
· n̂ds
S
s ∂t
~
~ = − ∂B
~ ×E
⇒ ∇
∂t
I
(6.12)
(6.13)
(6.14)
Además, encontramos la fuerza de Lorentz, dada por
~ + ν~ × B)
~
F~ = q(E
(6.15)
6.1. Ecuaciones de Maxwell
285
~ debido al desplazamiento de las
Vimos también que, en un dieléctrico, con polarización P,
cargas ligadas bajo la acción de un campo, hay una densidad de carga de polarización
ρP dada por
~
~ ·P
ρP = −∇
(6.16)
y aparece una corriente de polarización, de densidad dada por
~
~JP = ∂P
∂t
(6.17)
que satisface la ecuación de continuidad,
~
~ · ~JP = ∇
~ · ∂P = − ∂ρP
∇
∂t
∂t
(6.18)
Como la carga de polarización también produce un campo eléctrico, entonces
~ ~
~ = ρ + ρP = ρ − ∇ · P
~ ·E
∇
ε0
ε0
ε0
~ + P)
~ =ρ
~ · (ε0 E
∇
~ =ρ
~ ·D
⇒ ∇
6.1.2.
Ley de Gauss en un dieléctrico
(6.19)
(6.20)
(6.21)
Corriente de desplazamiento
James Clerk Maxwell nació en Escocia en 1831. En sus trabajos, Maxwell formuló
~ y ∇×,
~
sus resultados como función de los operadores vectoriales ∇·
que habían sido
empleados anteriormente por Stokes.
Una de sus observaciones fue que, de la misma forma que las cargas de polarización
en un dieléctrico producen un campo eléctrico, la corriente de polarización debe producir
un campo magnético. Así, la Ley de Ampere en un dieléctrico debe ser reformulada:
~
~ = µ0 (~J + ~JP ) = µ0~J + µ0 ∂P
~ ×B
∇
∂t
o en forma integral,
I
~ · d~l = µ0~J + µ0 ∂
B
∂
C
Z
S
~ · n̂ds
P
(6.22)
(6.23)
Para ver de qué forma se podría manifestar la corriente de polarización, vamos a
considerar que ocurre durante la carga o descarga de un capacitor con un dieléctrico
entre las placas.
6.1. Ecuaciones de Maxwell
286
Figura 6.1: la corriente de conducción pasa a través de S1 , pero no a
través de S2 . Sólo el desplazamiento
En la ausencia de un dieléctrico tendremos
~ = µ0~J
~ ×B
∇
~ = µ0 ∇ · ~J = 0
~ ×B
∇·∇
⇒ ∇ · ~J = 0
(6.24)
(6.25)
(6.26)
pero las cargas sobre las placas (cargas libres) están variando con el tempo. Luego,
deberíamos tener (contradiciendo el último resultado) que
~ · ~J = − ∂ρ
∇
∂t
para que sea consistente con la conservación de la carga. Por otro lado,
~= ρ
~ ·E
∇
ε0
.
~
~
∂/∂t
⇒ ρ = ε0 ∇ · E
!
~
∂ρ
∂ ~ ~
∂
E
~ · ε0
= ε0 ∇ · E = ∇
∂t
∂t
∂t
De modo que la ecuación de continuidad puede ser escrita como
!
~
∂
E
~ · ~J = ∇
~ · ε0
∇
∂t
!
~
~ · ~J + ε0 ∂E = 0
∇
∂t
(6.27)
(6.28)
(6.29)
(6.30)
(6.31)
(6.32)
6.2. Ondas electromagnéticas
287
Luego, para satisfacer la conservación de la carga, tendremos (en el vacío)
!
~
~
∂E
∂
E
~ = µ0 ~J + ε0
~ ×B
= µ0~J + µ0 ε0
∇
∂t
∂t
(6.33)
~
y en la presencia de un dieléctrico con polarización P
!
~
~
∂ ~ ~
∂
E
∂
P
~ = µ0 ~J + ε0
~ ×B
= µ0~J + µ0
∇
+
ε0 E + P
∂t
∂t
∂t
(6.34)
~
~ = µ0~J + µ0 ∂D
~ ×B
⇒ ∇
∂t
Finalmente, las ecuaciones de Maxwell generales son las siguientes:

~ 
∂
D

~ = ~J +
~ ×H

∇

∂t 

(


~ =ρ
~ = ε0 E
~ +P
~
~ ·D
∇
D
~
~ = µ0 (H
~ + M)
~

B

~ = − ∂B
~ ×E

∇


∂t



~ =0
~ ·B
∇
6.2.
Ondas electromagnéticas
6.2.1.
La ecuación de ondas
(6.35)
(6.36)
Consideremos las ecuaciones de Maxwell en el vacío, en una región en ausencia de
cargas y corrientes
~
~ = µ0 ε0 ∂E
~ ×B
∇
∂t
~
~
∇·E =0
(6.37)
~
~ = − ∂B
~ ×E
∇
∂t
~ = 0.
~ ·B
∇
(6.39)
(6.38)
(6.40)
Vamos a suponer el caso más simple donde
~ = E(z,
~ t)
E
(6.41)
~ = B(z,
~ t).
B
(6.42)
6.2. Ondas electromagnéticas
288
Para un vector que sólo depende de z y t, tenemos
~ = ∂Az
~ ·A
∇
∂z
~ = − ∂Ay ı̂ + ∂Ax ̂,
~ ×A
∇
∂z
∂z
(6.43)
(6.44)
entonces tenemos
(1)
∂By
∂Bx
−
ı̂ +
̂ = µ0 ε0
∂z
∂z
(2)
−
∂Ey
∂Ex
∂Ez
ı̂ +
̂ +
k̂
∂t
∂t
∂t
∂By
∂Ey
∂Ex
∂Bx
∂Bz
ı̂ +
̂ = −
ı̂ −
̂ −
k̂
∂z
∂z
∂t
∂t
∂t
(3)
(4)
(6.45)
(6.46)
∂Ez
=0
∂z
(6.47)
∂Bz
=0
∂z
(6.48)
.
Las ecuaciones anteriores dan
∂Ez
∂Ez
∂Bz
∂Bz
=
=0=
=
∂t
∂z
∂t
∂z
(6.49)
de forma que Ez y Bz son constantes. Por simplicidad tomaremos que
Ez = Bz = 0.
(6.50)
Las demás componentes se comportan como dos sistemas independientes
∂By
∂Ex
= −µ0 ε0
∂z
∂t
∂By
∂Ex
=−
∂z
∂t
∂Ey
∂Bx
= µ0 ε0
∂z
∂t
∂Ey
∂Bx
=−
∂z
∂t
(6.51)
El segundo par de ecuaciones sólo difiere del primero por las sustituciones siguientes
Ex → Ey
(6.52)
By → −Bx
(6.53)
6.2. Ondas electromagnéticas
289
de forma que sólo vamos a resolver el primer par

∂2 By
∂By
∂Ex
∂2 Ex



= −µ0 ε0
⇒
=
−µ
ε
0
0

 ∂z
∂t
∂t∂z
∂z 2




 ∂Ex = − ∂By
∂z
∂t
por otro lado

∂By
∂Ex



= −µ0 ε0

 ∂z
∂t




 ∂Ex = − ∂By
∂z
∂t






⇒
∂2 By
∂2 Ex
=− 2
∂z∂t
∂t





⇒
∂2 By
∂2 Ex
= −µ0 ε0 2
∂z∂t
∂t






⇒
∂2 By
∂2 Ex
=
−
∂t∂z
∂z 2





⇒
∂2 By
∂2 B y
−
µ
ε
= 0 (6.54)
0 0
∂z 2
∂t 2
⇒
∂2 Ex
∂2 Ex2
−
µ
ε
= 0, (6.55)
0 0
∂z 2
∂t 2
luego tanto Ex como By satisfacen la ecuación
1 ∂2 f
∂2 f
−
=0
∂z 2 ν 2 ∂t 2
(6.56)
y lo mismo ocurre para Ex y By en el segundo sistema de ecuaciones. De este modo,
todas las componentes de los campos electromagnéticos satisfacen la ecuación de ondas
unidimensional, con una velocidad de propagación
1
ν=√
µ0 ε0
(6.57)
como
10−9
F
y
4π · 8, 98755 m
H
−7
entonces
µ0 = 4π · 10
m
m
ν∼
=c
= 2, 99792 · 108
s
ε0 ∼
=
donde c es la velocidad de la luz.
Así, concluimos que la luz es una onda electromagnética.
6.2.2.
Ondas electromagnéticas planas
La solución general de la ecuación de ondas unidimensional
∂2 f
1 ∂2 f
−
=0
∂z 2 ν 2 ∂t 2
(6.58)
6.2. Ondas electromagnéticas
290
es
f (z, t) = F (z − νt) + G(z + νt)
(6.59)
donde F y G son funciones arbitrarias. Físicamente, F representa un perfil cualquiera de
onda propagándose en el sentido de z − positivo (onda progresiva) y G es una onda en
sentido opuesto (onda regresiva).
Vamos a considerar una solución para el primer sistema que se propaga en un solo
sentido, por ejemplo, en el sentido positivo del eje z
Ex (z, t) = Ex (z − ct)
(6.60)

∂By
∂Ex
1 ∂Bx


= −µ0 ε0
= 2

 ∂z
∂t
c ∂t
(6.61)



 ∂Ex = − ∂By
∂z
∂t
realizando el cambio de variables ζ ≡ z − ct tenemos
∂
d
→
∂z
dζ
∂
d
→ −c
∂t
dζ
de modo que
dBy
1 dEx
=
dζ
c dζ







dBy 
dEx



=c
dζ
dζ
By (z, t) =
(6.62)
(6.63)
1
Ex (z − ct),
c
(6.64)
por lo tanto
~ = Ex (z − ct)ı̂
E
(6.65)
~ = 1 Ex (z − ct)̂ = 1 k̂ × E.
~
B
c
c
(6.66)
En general, las ondas son transversales a la dirección de propagación k̂, y tenemos
~
~ = 1 k̂ × E
B
c
(6.67)
6.2. Ondas electromagnéticas
6.2.3.
291
Ondas planas monocromáticas
Hasta ahora no hemos especificado la dependencia de la variable z − ct. La forma
más simple de onda es aquella para la cual esta dependencia es oscilatoria, con una
frecuencia angular ω en el tiempo
~ = A cos(kz − ωt + δ)ı̂,
E
(6.68)
donde k = ω/c es el número de onda y A es la amplitud de la onda. A partir de este
resultado tenemos que
~ = A cos(kz − ωt + δ)̂.
B
(6.69)
c
Este tipo de onda recibe el nombre de harmónica o monocromática. Estas ondas cumplen
que
2π
ω
1
ν=
T
2π
λ=
= cT
k
φ ≡ kz − ωt + δ
δ
T =
periodo temporal
frecuencia
(6.70)
periodo espacial; longitud de onda
fase de la onda
constante de fase
Figura 6.2: Onda electromagnética linealmente polarizada en el plano
en la dirección x positiva con una velocidad c.
6.2. Ondas electromagnéticas
292
Además de ser transversal a la dirección de propagación, el campo eléctrico
permanece siempre en un mismo plano. Es por esto que se dice que la onda es linealmente
polarizada.
En el caso general de una onda electromagnética plana monocromática propagándose
en una dirección arbitraria µ y linealmente polarizada en una dirección ε̂ es
~ r −ωt+δ)
~ = Re[Aei(k·~
E
]ε̂,
k~ = k µ̂
~ = 1 µ̂ × E
~
B
c
6.2.4.
(6.71)
(6.72)
Energía y vector de Poynting
La densidad de energía electromagnética en el vacío es
U=
1
1 B2
ε0 E 2 +
= UE + UM .
2
2 µ0
(6.73)
La tasa de variación temporal de U es, por lo tanto
~
~
∂U
~ · ∂E + 1 B
~ · ∂B .
= ε0 E
∂t
∂t
µ0
∂t
(6.74)
Para calcular el segundo término, vamos a usar las ecuaciones de Maxwell. Usando la
Ley de Ampere tendremos
~
~ = µ0~J + µ0 ε0 ∂E
~ ×B
∇
∂t
~
∂E
~ − µ0~J
~ ×B
µ0 ε0
=∇
∂t
~
~
~
~ · ∂E = E
~ · ∇ × B − ~J · E,
~
ε0 E
∂t
µ0
(6.75)
(6.76)
(6.77)
por otro lado, usando la Ley de inducción de Faraday tendremos
~
~ = − ∂B
~ ×E
∇
∂t
~
∂B
~
~ ×E
= −∇
∂t
~ ∂B
~
~
B
B
~
~ × E,
·
=− ·∇
µ0 ∂t
µ0
(6.78)
(6.79)
(6.80)
6.2. Ondas electromagnéticas
293
de modo que
~
~
∂U
~ · ∂E + 1 B
~ · ∂B
= ε0 E
∂t
∂t
µ0
∂t
∂U ~ ~
1 ~ ~
~ −E
~ · (∇
~
~ × B)],
−
= J · E + [B
· (∇ × E)
∂t
µ0
(6.81)
(6.82)
pero conociendo la siguiente igualdad
~ · (∇
~ −E
~ · (∇
~ =∇
~ × B),
~
~ · (E
~ × E)
~ × B)
B
(6.83)
de modo que
∂U ~ ~
~
~ · S,
=J ·E +∇
∂t
~ como
donde definimos el vector de Poynting S
−
~ ×B
~
~= 1E
S
µ0
(6.84)
(6.85)
que representa la densidad de corriente de energía electromagnética. En particular, en
la ausencia de cargas y corrientes tendremos
~ + ∂U = 0
~ ·S
∇
∂t
que es la Ley de Conservación de la energía electromagnética.
(6.86)
294
6.2. Ondas electromagnéticas
Ejercicios Propuestos
Ecuaciones de Maxwel.
1. Escriba las ecuaciones de Maxwell generales (considerando un material dieléctrico y
magnético) en su forma integral y diferencial. Explique el procedimiento que le permite
pasar de su forma integral a su forma diferencial señalando los teoremas que utiliza.
Defina cada una de las ecuaciones de Maxwell (nombre y significado).
2. Una onda electromagnética sinusoidal con una frecuencia de 40 [mHz] se desplaza en
el espacio libre en la dirección de las x.
(a) Determine la longitud y periodo de la onda.
(b) En algún punto y en algún momento, el campo eléctrico tiene su valor máximo,
750 [N/C ], y está orientado a lo largo del eje de las y. Calcule la magnitud y dirección del campo magnético en este punto y momento.
(c) Escriba expresiones para la variación espacio-tiempo de las componentes de los
campos eléctrico y magnético para esta onda.
3. Demuestre que el siguiente campo electromagnético satisface las ecuaciones de
Maxwell:
Ex
= Ey = By = 0
Ez = cos(y − ct)
1
cos(y − ct)
Bx =
c
(6.87)
(6.88)
(6.89)
296
Ejercicios propuestos ecuaciones de Maxwel.
4. Una onda electromagnética plana monocromática se propaga en el vacío en la dirección
positiva del eje z. La onda se mueve en una región donde no hay cargas, es decir, ρ = 0
y donde no hay materiales conductores, es decir, ~J = 0. Si el campo magnético de dicha
onda viene descrito por la expresión:
~ t) = −b sin(kz − ωt)ı̂ + b cos(kz − ωt)̂
B(z,
(6.90)
~ t) de la onda.
(a) Encuentre el campo eléctrico E(z,
~ t) y B(z,
~ t), respectivamente y
(b) Encuentre los módulos E0 y B0 de los vectores E(z,
encuentre la relación entre ellos.
~ t).
(c) Encuentre el vector de Poynting S(z,
~ t), B(z,
~ t) y S(z,
~ t), y señale la
(d) Dibuje esquemáticamente los tres vectores E(z,
relación entre ellos.
5. Consideremos una onda monocromática plana que se propaga en el vacío a lo largo
del eje x y que viene descrita por el campo eléctrico en la forma:
~ t) = E0y sin(kx − ωt)̂ + E0z cos(kx − ωt)k̂
E(x,
(6.91)
~ t).
(a) Encuentre el campo magnético B(x,
~ t) y B(x,
~ t), y el ángulo que
(b) Calcule el ángulo que hacen entre sí los campos E(x,
hace cada campo con la dirección de propagación ı̂.
(c) Exprese el campo magnético como función del campo eléctrico.
~ t) y B(x,
~ t), respectivamente y
(d) Encuentre los módulos E0 y B0 de los vectores E(x,
encuentre la relación entre ellos.
~ t).
(e) Encuentre el vector de Poynting S(x,
Anexos
297
Anexo A
Prefijos y letras griegas
Alfabeto Griego
Alpha
Beta
Gamma
Delta
Épsilon
Zeta
Eta
Teta
A
B
Γ
∆
E
Z
H
Θ
α
β
γ
δ
ε
ζ
η
θ
Iota
Kappa
Lambda
Mu
Nu
Xi
Ómicron
Pi
I
K
Λ
M
N
Ξ
O
Π
ι
κ
λ
µ
ν
ξ
o
π
Ro
Sigma
Tau
Úpsilon
Fi
Ji
Psi
Omega
P
Σ
T
Υ
Φ
X
Ψ
Ω
ρ
σ
τ
υ
φ
χ
ψ
ω
Prefijos para las potencias de diez
factor
101
102
103
106
109
1012
1015
1018
1021
1024
prefijo
deca
hecto
kilo
mega
giga
tera
peta
exa
zetta
yotta
símbolo
d
h
k
M
G
T
P
E
Z
Y
factor
10−1
10−2
10−3
10−6
10−9
10−12
10−15
10−18
10−21
10−24
prefijo
deci
centi
mili
micro
nano
pico
femto
atto
zepto
yocto
símbolo
d
c
m
µ
n
p
f
a
z
y
300
Anexo B
Derivadas vectoriales
Coordenadas cartesianas (x, y, z)
~ = Ax âx + Ay ây + Az âz
A
∂V
∂V
∂V
âx +
ây +
âz
∂x
∂y
∂z
~ = ∂Ax + ∂Ay + ∂Az
∇·A
∂x
∂y
∂z


âx ây âz
∂
∂ ∂V 

~=
∇×A


 ∂x ∂y ∂z 
~x A
~y A
~z
A
∂Ay
∂Ay ∂Ax
∂Ax
∂Az
∂Az
−
âx +
−
ây +
+
âz
=
∂y
∂z
∂z
∂x
∂x
∂y
∇V =
∇2 V =
∂2 V
∂2 V
∂2 V
+
+
∂x 2
∂y2
∂z 2
302
Coordenadas cilíndricas (ρ, φ, z)
~ = Aρ âρ + Aφ âφ + Az âz
A
∂V
1 ∂V
∂V
âρ +
âφ +
âz
∂ρ
ρ ∂φ
∂z
~ = 1 ∂ (ρAρ ) + 1 ∂Aφ + ∂Az
∇·A
ρ ∂ρ
ρ ∂φ
∂z


âρ ρâφ âz
 ∂
∂
∂V 
1

~= 
∇×A


ρ  ∂ρ ∂φ ∂z 
~z
~ ρ ρA
~φ A
A
∂Aφ
∂Aρ
∂Aρ
1 ∂Az
∂Az
1 ∂
=
−
âρ +
−
âφ +
(ρAφ ) −
âz
ρ ∂φ
∂z
∂z
∂ρ
ρ ∂ρ
∂φ
1 ∂
∂2 V
∂V
1 ∂2 V
2
∇ V =
+
ρ
+ 2
ρ ∂ρ
∂ρ
ρ ∂φ2
∂z 2
∇V =
Coordenadas esféricas (r, θ, φ)
~ = Ar âr + Aθ âθ + Aφ âφ
A
∇V =
~=
∇·A
~=
∇×A
=
∇2 V =
1 ∂V
1 ∂V
∂V
âr +
âθ +
âφ
∂r
r ∂θ
r sin θ ∂φ
1 ∂ 2
1
∂
1 ∂Aφ
(r Ar ) +
(Aθ sin θ ) +
2
r sin θ ∂θ
r sin θ ∂φ
r ∂r


âr r âθ (r sin θ)âφ
∂

∂
∂V
1




2
∂φ

r sin θ  ∂r ∂θ
~r rA
~ θ (r sin θ)A
~φ
A
1
∂
∂Aθ
1
1 ∂Ar
∂
1 ∂
∂Ar
(Aφ sin θ) −
âr +
− (rAφ ) âθ +
(rAθ ) −
âφ
r sin θ ∂θ
∂φ
r sin θ ∂φ
∂r
r ∂r
∂θ
1 ∂
∂2 V
∂V
1
∂
∂V
1
r2
+ 2
sin θ
+
2
2
∂r
∂θ
r ∂r
r sin θ ∂θ
r 2 sin θ ∂φ2
Anexo C
Constantes Físicas
Constantes Físicas[2]
Cantidad (Unidad)
Símbolo
Valor1
Masa del electrón
me
9, 10938188(72) × 1031 [kg]
5, 485799110(12) × 10−4 [u]
0, 510998902(21) [MeV /c 2 ]
Masa del protón
mp
1, 67262158(13) × 10−27 [kg]
1, 00727646688(13) [u]
938, 271998(38) [MeV /c 2 ]
Masa del neutrón
mn
1, 67492716(13) × 10−27 [kg]
1, 00866491578(55) [u]
939, 565330(38) [MeV /c 2 ]
Número de Avogadro
NA
6, 02214199(47) × 1023 [particulas/mol]
Unidad de masa atómomica
u
1, 66053886(28) × 10−27 [kg]
Magnetón de Bohr
µB =
Radio de Bohr
a0 =
Constante de Coulomb
Ke =
Carga elemental
e
1, 60217653(14) × 10−19 [C ]
Electrón volt
eV
1, 60217653(14) × 10−19 [J]
Cuanto de flujo magnético
Φ0 =
Permeabilidad del espacio libre
µ0
Permitividad del espacio libre
ε0 =
Rapidez de la luz en el vacío
c
e~
2m
~2
me e2 ke
1
1πε0
h
2e
1
µ0 c 2
9, 27400949(80) × 10−24 [J/T ]
5, 2917772108(18) × 10−11 [m]
8, 987551788 . . . × 109 [N · m2 /C 2 ]
2, 06783372(18) × 10−15 [T · m2 ]
4π × 10−7 [T · m/A]
8, 854187817 . . . × 10−12 [C 2 /N · m2 ]
2, 99792458 × 108 [m/s]
304
Anexo D
Premios Nobel de Física
The Nobel Prize in Physics has been awarded 104 times to 189 Nobel Laureates
between 1901 and 2010. John Bardeen is the only Nobel Laureate who has been awarded
the Nobel Prize in Physics twice, in 1956 and 1972. This means that a total of 188
individuals have received the Nobel Prize in Physics.[3]
2011 Saul Perlmutter, Brian P. Schmidt, Adam G. Riess
2010 Andre Geim, Konstantin Novoselov
2009 Charles Kuen Kao, Willard S. Boyle, George E. Smith
2008 Yoichiro Nambu, Makoto Kobayashi, Toshihide Maskawa
2007 Albert Fert, Peter Grünberg
2006 John C. Mather, George F. Smoot
2005 Roy J. Glauber, John L. Hall, Theodor W. Hänsch
2004 David J. Gross, H. David Politzer, Frank Wilczek
2003 Alexei A. Abrikosov, Vitaly L. Ginzburg, Anthony J. Leggett
2002 Raymond Davis Jr., Masatoshi Koshiba, Riccardo Giacconi
2001 Eric A. Cornell, Wolfgang Ketterle, Carl E. Wieman
2000 Zhores I. Alferov, Herbert Kroemer, Jack S. Kilby
306
1999 Gerardus ’t Hooft, Martinus J.G. Veltman
1998 Robert B. Laughlin, Horst L. Störmer, Daniel C. Tsui
1997 Steven Chu, Claude Cohen-Tannoudji, William D. Phillips
1996 David M. Lee, Douglas D. Osheroff, Robert C. Richardson
1995 Martin L. Perl, Frederick Reines
1994 Bertram N. Brockhouse, Clifford G. Shull
1993 Russell A. Hulse, Joseph H. Taylor Jr.
1992 Georges Charpak
1991 Pierre-Gilles de Gennes
1990 Jerome I. Friedman, Henry W. Kendall, Richard E. Taylor
1989 Norman F. Ramsey, Hans G. Dehmelt, Wolfgang Paul
1988 Leon M. Lederman, Melvin Schwartz, Jack Steinberger
1987 J. Georg Bednorz, K. Alexander Müller
1986 Ernst Ruska, Gerd Binnig, Heinrich Rohrer
1985 Klaus von Klitzing
1984 Carlo Rubbia, Simon van der Meer
1983 Subramanyan Chandrasekhar, William Alfred Fowler
1982 Kenneth G. Wilson
1981 Nicolaas Bloembergen, Arthur Leonard Schawlow, Kai M. Siegbahn
1980 James Watson Cronin, Val Logsdon Fitch
1979 Sheldon Lee Glashow, Abdus Salam, Steven Weinberg
1978 Pyotr Leonidovich Kapitsa, Arno Allan Penzias, Robert Woodrow Wilson
1977 Philip Warren Anderson, Sir Nevill Francis Mott, John Hasbrouck van Vleck
307
1976 Burton Richter, Samuel Chao Chung Ting
1975 Aage Niels Bohr, Ben Roy Mottelson, Leo James Rainwater
1974 Sir Martin Ryle, Antony Hewish
1973 Leo Esaki, Ivar Giaever, Brian David Josephson
1972 John Bardeen, Leon Neil Cooper, John Robert Schrieffer
1971 Dennis Gabor
1970 Hannes Olof Gösta Alfvén, Louis Eugène Félix Néel
1969 Murray Gell-Mann
1968 Luis Walter Alvarez
1967 Hans Albrecht Bethe
1966 Alfred Kastler
1965 Sin-Itiro Tomonaga, Julian Schwinger, Richard P. Feynman
1964 Charles Hard Townes, Nicolay Gennadiyevich Basov, Aleksandr Mikhailovich
Prokhorov
1963 Eugene Paul Wigner, Maria Goeppert-Mayer, J. Hans D. Jensen
1962 Lev Davidovich Landau
1961 Robert Hofstadter, Rudolf Ludwig Mössbauer
1960 Donald Arthur Glaser
1959 Emilio Gino Segrè, Owen Chamberlain
1958 Pavel Alekseyevich Cherenkov, Il´ja Mikhailovich Frank, Igor Yevgenyevich
Tamm
1957 Chen Ning Yang, Tsung-Dao (T.D.) Lee
1956 William Bradford Shockley, John Bardeen, Walter Houser Brattain
1955 Willis Eugene Lamb, Polykarp Kusch
308
1954 Max Born, Walther Bothe
1953 Frits (Frederik) Zernike
1952 Felix Bloch, Edward Mills Purcell
1951 Sir John Douglas Cockcroft, Ernest Thomas Sinton Walton
1950 Cecil Frank Powell
1949 Hideki Yukawa
1948 Patrick Maynard Stuart Blackett
1947 Sir Edward Victor Appleton
1946 Percy Williams Bridgman
1945 Wolfgang Pauli
1944 Isidor Isaac Rabi
1943 Otto Stern
1942 No Nobel Prize was awarded this year.
1941 No Nobel Prize was awarded this year.
1940 No Nobel Prize was awarded this year.
1939 Ernest Orlando Lawrence
1938 Enrico Fermi
1937 Clinton Joseph Davisson, George Paget Thomson
1936 Victor Franz Hess, Carl David Anderson
1935 James Chadwick
1934 No Nobel Prize was awarded this year.
1933 Erwin Schrödinger, Paul Adrien Maurice Dirac
1932 Werner Karl Heisenberg
309
1931 No Nobel Prize was awarded this year.
1930 Sir Chandrasekhara Venkata Raman
1929 Prince Louis-Victor Pierre Raymond de Broglie
1928 Owen Willans Richardson
1927 Arthur Holly Compton, Charles Thomson Rees Wilson
1926 Jean Baptiste Perrin
1925 James Franck, Gustav Ludwig Hertz
1924 Karl Manne Georg Siegbahn
1923 Robert Andrews Millikan
1922 Niels Henrik David Bohr
1921 Albert Einstein
1920 Charles Edouard Guillaume
1919 Johannes Stark
1918 Max Karl Ernst Ludwig Planck
1917 Charles Glover Barkla
1916 No Nobel Prize was awarded this year.
1915 Sir William Henry Bragg, William Lawrence Bragg
1914 Max von Laue
1913 Heike Kamerlingh Onnes
1912 Nils Gustaf Dalén
1911 Wilhelm Wien
1910 Johannes Diderik van der Waals
1909 Guglielmo Marconi, Karl Ferdinand Braun
310
1908 Gabriel Lippmann
1907 Albert Abraham Michelson
1906 Joseph John Thomson
1905 Philipp Eduard Anton von Lenard
1904 Lord Rayleigh (John William Strutt)
1903 Antoine Henri Becquerel, Pierre Curie, Marie Curie, née Sklodowska
1902 Hendrik Antoon Lorentz, Pieter Zeeman
1901 Wilhelm Conrad Röntgen
Bibliografía
[1] http://www.pickatrail.com/jupiter/location/europe/greece/magnesia.html.
[2] CODATA. http://physics.nist.gov/cuu/constants/index.html. Estas constantes son los
valores recomendados en 1998 por CODATA, sobre la base de un ajuste por mínimos
cuadrados de los datos de diferentes medidas. Para obtener una lista más completa,
vea PJ Mohr y Taylor BN, Rev. mod. Phys.. 72:351, 2000.
[3] The Nobel Organizations. http://nobelprize.org/nobel_prizes/physics/laureates/index.html.
Fecha de acceso: 01 de abril, 2011.
[4] Raymond A. Serway. Electricidad y Magnetismo. McGRAW-HILL, tercera edicion
edition.
311