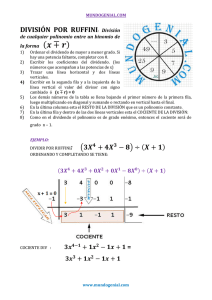
LA DIVISION es una operación que tiene por objeto, dado el

LA DIVISION es una operación que tiene por objeto, dado el producto de dos factores
(dividendo) y uno de los factores (divisor), hallar el otro factor (cuociente)
LEY DE LOS SIGNOS es la misma que la de la multiplicación
Signos iguale = +
y signos diferentes = -
Ejemplo + ab 4 x 3 : ab2 x
b2 x2
Como Ud. Ve se aplican las reglas de las potencias a los exponentes
DIVISION DE MONOMIOS.
EJEMPLO : 4a 5 b 2 x : 2a 4 b 2
4a 5 b 2 x
2a 4 b 2
2ax
-20m x a 2 y 4a 3 : 5mxa 3 y 2a 2
4xy 2a 1
DIVISION DE POLINOMIO POR MONOMIO: Se divide cada término del
polinomio por el monomio.
Ejemplo :
(3a 3
6a 2 b 9ab2 ) : 3a
3a 3
6a 2 b 9ab2
3a
3a 3
3a
6a 2 b
3a
9ab2
3a
a2
2ab 3b 2
DIVISION DE DOS POLINOMIOS.
1.- se ordena el dividendo y el divisor en relación a una letra y a la potencia.
2.- Se divide el primer termino del dividendo entre el primer termino del divisor lo que
da el primer termino del cociente.
3.- Se multiplica este primer término del cociente por el divisor y el resultado se resta
del polinomio dividendo. Con este último resultado obtenido se continúa el proceso.
Ejemplo: 3x 2
2x 8
x 2
EJERCICIOS PROPUESTOS:
1.3.-
5m 2 n : m 2 n
15m 2 n 4 x : 3m 2 n
2.- 8a 2 x 3 : 8a 2 x 3
4.- 16m 6 n 4 : 5m 2 n 3
5.-
2m 2 n 6 : 3m 2 n 6
6.-
7.-
7 x m 3 y m 1 : 8x 2 y 2
8.- a m n b x
9.- x 2n 3 y 3n 1 : x 3n 3 y 2n
11.-
1
3 3
4 2
a b:
ab
5
5
15.-
2a x 4 b m 3 :
a
: a mb a
10.- 12x 2n 3 y 2n 1 : 16x 3n 3 y 2n
1 2 2
x :
2
3
13.-
3a x b m : ab2
1 4 m
a b
2
3
12.-
3 3
4 2
a b:
a b
5
5
14.-
1 x3 m5 2 3 x4 m
a b c : a b
15
5
16.-
1
1
3 m n
3 3
a b :
b
4
2
Polinomio por monomio.
1.- (a 2
ab) : a
3.- (3a 3
5ab2
5.- (4x 8 10x 6
2.- (3x 2 y 3
6a 2b3 ) : 2a
4.- ( x 3
5x 4 ) : 2 x 3
6.- (6m3 8m 2 n 20mn2 ) : 2m
7.- (8m9 n 2 10m7 n 4
8.- (2a m 3a m
10.- ( x m
2
2
5x m
6x m
3
2
x) : x
4
3
1
14.- ( m 4
4
2 3
m n
3
1
1 x
a
4
1
4x 2
x) : x
20m5 n 6 12m3 n8 ) : 2m2
6m m 4 ) : 3a 3
1
12.- ( x 2
2
2
16.- ( a x
3
5a 2 x 4 ) : 3x 2
1
9.- (a x
xm 1) : xm
2
am 1) : a2
11.- (12a x
1
13.- ( a 3
3
3 2 2 1 2
m n ): m
8
4
2 x 1 x
a ): a
5
6
2
2
15. ( x 4 y 3
3
1
16a x 3 ) : 4a x
3 2
a
5
1 3 4
x y
5
5
1
3
a) :
4
5
1 2 5
x y
4
xy 6 ) :
1 3
xy
5
17.- (
3 n1 m
a x
4
1 n m
a x
8
2
2 n1 m
2 3 2
a x ):
a x
3
5
1
División de polinomios.
1.- (a 2
2a 3) : (a 3)
2.- (a 2
3.- ( x 2
20 x) : ( x 5)
4.- (m 2 11m 30) : (m 6)
2a 3) : (a 1)
5.- ( x 2 15 8x) : (3 x)
6.- (6 a 2
5a) : (a 2)
7.- (6 x 2
8.- ( 15x 2
8y 2
xy 2 y 2 ) : ( y 2 x)
9.- (a 4
a2
2a 1) : (a 2
10.- ( x 5 12x 2 15x) : ( x 2
a 1)
11.- (m5
5m 4 n 20m 2 n 3 16mn4 ) : (m 2
12.- ( x 4
x2
14.- (24x 5
2 x 1) : ( x 2
x 1)
52x 4 y 38x 3 y 2
8x 7 y 4
16.- ( x 3
3xyz) : ( x 2
y3
17.- (m2a
18.- ( x 2a
2
2
19.- (a 2n b3
20.- (a m
x
z3
m 2a
x 2a
1
3
6x 5 y 6
4m2a
4x 2a
a 2n 1b 4
4
2m2a
a mb x
a xbm
1
21.- ( a 2
6
5
ab
36
1 2
1
b ):( a
6
3
3
23.- ( m 4
5
1 3
17 2 2
m n
m n
10
60
3
24.- ( x 5
8
21 4
x
40
47 3
x
120
26xy 4
1
z2
2a 2n 4b 7
7x 2
3x 2
4 y 5 ) : (8x 3 12x 2 y 6xy 2
y3 )
2
3
2x 3 y 2
yz)
m 2 a 3 ) : (m a
xa
1
3xy 4 )
3
ma
1
ma 2 )
xa 2 )
a 2n 5 ) : (a n b a a 1b 2
2a a 2b3
a n 3b 4 )
bx )
1
b)
2
1
22.- ( x 2
3
7
mn 3
6
79 2
x
120
2x 5
3xy10 ) : ( x 5
2m2a
b m x ) : (a x
4x 6) : ( x 4
xy xz
x 2a 7 ) : ( x a
a 2n 2 b 5
6a 3
5x 3 y 8
y2
2x 5)
2mn 8n 2 )
13. ( x 6
33x 2 y 3
15.- ( x11 5x 9 y 2
22xy) : (2 y 3x)
7
xy
10
1 2
y ) : (x
3
3
n4 ) : ( m2
2
2n 2
mn )
1
1
1
x
):(
10
10
2
1 2
x
3
1 1 3
x x )
4 4
2
y)
5
2)