Derivada de una función constante f(x) = k, entonces f´(x)

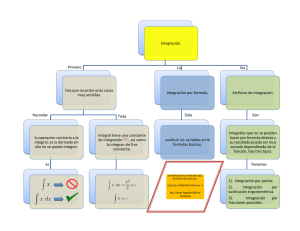
REGLAS DE DERIVACIÓN
Formula:
f(x) = k, entonces f´(x)=0.
Derivada
de
una
función
constante
Descripción
Si f(x) = k, donde k es cualquier numero real, entonces f´(x)=0. Es decir, la
derivada de una función constante es cero.
Ejemplo
Formula:
f(x)=x, entonces f´(x)=1.
Derivada de la
función
identidad
Descripción
Si f(x)=x, entonces f´(x)=1. Es decir, la derivada de una función identidad es
uno.
Ejemplo
Formula:
f(x) = xn, entonces f´(x) = nxn-1
Derivada
de
una potencia
Descripción
Si f(x) = xn, con n
entonces f´(x) = nxn-1
Ejemplo:
Formula:
f(x) = kg(x), entonces f´(x)=kg´(x)
Derivada
del
múltiplo
constante
Descripción:
Si f(x) = kg(x), con k
y g una función derivable, entonces f´(x)=kg´(x)
Ejemplo
f(x) = 3x
f´(x) = 3
=3*1=3
Formula
t(x)=f(x) g(x), entonces, t´(x)=f´(x) g´(x).
Derivada de la
suma/resta de
funciones
Descripción
Si f y g son dos funciones derivables, y t(x)=f(x) g(x), entonces,
t´(x)=f´(x) g´(x).
Ejemplo
Formula
(f(x)*g(x)) = f´(x)*g(x) + f(x)*g´(x)
Derivada
del
producto
de
dos funciones
Descripción
Si f y g son dos funciones derivables, entonces:
(f(x)*g(x)) = f´(x)*g(x) + f(x)*g´(x)
Ejemplo
*
Formula
(
)
Deriva
del
cociente
de
funciones
Descripción
Si f y g son dos funciones derivables y g(x)
(
Ejemplo
*
)
entonces:
Formula
[
] [
]
(
)
Derivada
de
funciones
compuestas:
(regla de la
cadena)
Descripción
La derivada de una función compuesta es igual al producto de la derivada de la
función externa calculada en la función interna, por la derivada de la función
interna. Si y = f(u) y u = g(x), tal que g es derivable en x y f es derivable en u, en
la notación de Leibniz se simboliza la regla de la cadena como:
Ejemplo
Formula
f(x) =
, entonces f´(x)=
Derivada de la
f(x) = ln x, entonces f´(x) =
función
logarítmica
y= g(x) y f(x)=
, entonces f´(x)=
Descripción
*
Sea f una función logarítmica se cumple que:
Si f(x) =
,a>0 ya
, entonces f´(x)=
Si f(x) = ln x, entonces f´(x) =
Si y= g(x) y f(x)=
, entonces f´(x)=
*
Ejemplo
*
Formula
Derivada de las
funciones
exponenciales
Descripción
Ejemplo
f(X) = ax, entonces f´(x) = ax * ln a
f(x) = ah(x), entonces f´(x) = ah(x) * ln a * h´(x)
f(x) = x, entonces f´(x) = x
Sea f una función exponencial se cumple que:
Si f(X) = ax, entonces f´(x) = ax * ln a
Si f(x) = x, entonces f´(x) = x
Si f(x) = ah(x), entonces f´(x) = ah(x) * ln a * h´(x)
*
Formula
Derivada de las
funciones
trigonométricas
Descripción
Ejemplo
Formula
Derivadas de
las funciones
trigonométricas
inversas
f(x) =sen x, entonces f´(x)= cos x
f(x) =cos x, entonces f´(x)= -sen x
f(x) =tan x, entonces f´(x)= sec2 x
f(x) =cot x, entonces f´(x)= -csc2 x
f(x) =sec x, entonces f´(x)= sec x * tan x
f(x) =csc x, entonces f´(x)= -csc x * cot x
f(x) =sen 4x f´(x)= 4 cos 4x
f(x) =cos 23x f´(x)= -23 sen 23x
f(x) =tan 2.03x f´(x)= 2.03sec2 2.03x
f(x) =cot 75x f´(x)= -75 csc2 75x
f(x) =sec 3.1x f´(x)= 3.1 sec 3.1x * tan 3.1x
f(x) =csc 46x f´(x)= -46 csc 46x * cot46 x
Descripción
f(x) =sen -1x, entonces f´(x)=
√
-1
f(x) =cos x, entonces f´(x)=
f(x) =tan -1x, entonces f´(x)=
f(x) =cot -1x, entonces f´(x)=
f(x) =sec -1x, entonces f´(x)=
f(x) =csc -1x, entonces f´(x)=
Ejemplo
 Derivar los términos de la ecuación con respecto a x.
 Aplicar las reglas de la derivada y la regla de la cadena.
 Despejar la derivada.
Formula
Derivación
implícita
Ejemplo
*