Diagramas de Bode de magnitud y fase

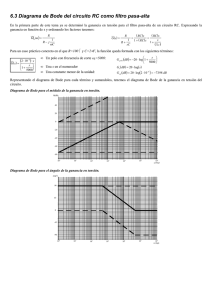
Diagramas de Bode de magnitud y fase
Diagramas de Bode de magnitud y fase de una constante
Dada la función circuital F(j~) = K, podemos expresarla en la forma:
F (j~) = )
K e j0 K > 0
K e jr K < 0
La magnitud en decibelios es FdB(~) = 20 log K . El diagrama de Bode de magnitud consiste de una recta horizontal que
puede estar por encima del eje de frecuencias, sobre el eje de frecuencias o por debajo del mismo, dependiendo de K .
Si K < 1, la recta está por debajo.
Si K > 1, la recta está por encima.
En cuanto a la fase, el diagrama de Bode correspondiente es una recta horizontal que es igual a cero si K > 0 y es igual a r si
K < 0.
Diagramas de Bode de magnitud y fase de un derivador
s
Un circuito derivador presenta una función de transferencia de la forma F (s) =
. En adelante se hará el siguiente cambio
~p
s
de variable S =
, con lo cual obtenemos el derivador normalizado F(S) = S; si hacemos la sustitución S = jX, obtene~p
mos:
F (jX) = jX = jXe j 2 .
r
La magnitud en decibelios de la función está dada por FdB (X) = 20 log X. El diagrama de Bode de magnitud es una recta
que pasa por la frecuencia característica y tiene una pendiente de 20 decibelios por década. La figura 1 ilustra el diagrama
de Bode de magnitud para un derivador.
En cuanto a la fase, el diagrama de Bode será la recta horizontal H (~) =
r
.
2
40
20
FdB (~)
0
-20
-40
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
Figura 1
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::
Diagramas de Bode de magnitud y fase de un circuito integrador
Un circuito integrador se caracteriza por la función de transferencia F (s) =
F (S) =
~p
,
s
1
.
S
Puede mostrarse que la magnitud de la función en decibelios está dada por:
FdB (~) =- 20 log `
~j
.
~p
Claramente se observa que el diagrama correspondiente es una recta que pasa por y tiene una pendiente de -20 decibelios
por década.
Es pertinente anotar que el integrador es el inverso multiplicativo del derivador y, en consecuencia, el diagrama de Bode del
integrador es el inverso aditivo del diagrama de Bode del derivador.
r
En cuanto a la fase, el diagrama de Bode correspondiente es la recta horizontal H (~) =- . La figura 2 muestra el diagra2
ma de Bode de magnitud para el integrador.
40
20
FdB (~)
0
-20
-40
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
Figura 2
Diagrama de Bode de magnitud de una función lineal
s
Una función circuital lineal presenta la forma F (s) = 1 +
& F (S) = 1 + S. Al efectuar la sustitución S = X, se obtiene
~p
F = (jX) = 1 + jX.
La magnitud en decibelios está dada por FdB (X) = 10 log 61 + X2 @ .
Para representar el diagrama de Bode correspondiente es necesario dibujar dos asíntotas y el punto de la gráfica correspondiente a la frecuencia característica, el cual denominaremos como la “corrección”.
Las asíntotas del diagrama de Bode de magnitud son las rectas que se obtienen para frecuencias por debajo y por encima
de la frecuencia característica, así:
1. Para frecuencias menores que ~p, obtenemos FdB(Ω < 1) = 0.
2. Para frecuencias mayores que ~p, obtenemos FdB(Ω > 1) = 20 log (Ω).
3. Para la frecuencia ~p, obtenemos FdB(Ω = 1) =3.
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::
La figura 3 ilustra el diagrama de Bode asintótico de magnitud para la función lineal.
La fase de la función lineal está dada por H (X) = a tan (X) .
Para dibujar el diagrama de Bode de fase es necesario trazar tres asíntotas, las cuales se deducen al analizar la expresión
matemática, así:
i. En el intervalo 0 < ~ < 0.1~p, la fase es prácticamente cero y en consecuencia obtenemos la asíntota H (X) = 0.
r r
ii. En el intervalo 0.1 ~p < ~ < 10 ~p, la fase es prácticamente lineal en escala logarítmica, así: H (X) = + log (X) .
4
4
r
Se puede notar que H (0.1~ p) = 0 y H (10~ p) = .
2
iii.En el intervalo ~ > 10~p, la fase es prácticamente de noventa grados, esto es, la asíntota es la recta horizontal
H (X ) = r 2 .
La figura 4 ilustra el diagrama asintótico de fase de la función.
40
20
FdB (~)
0
-20
-40
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
~0
10 ~0
100 ~0
Figura 3
r
H(~)
r/4
0
0.01 ~0
0.1~0
Figura 4
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::
Diagramas de Bode de magnitud y fase para el inverso multiplicativo de una función lineal
En este caso la función de transferencia es de la forma F(S) = (1+S)-1.
El estudiante puede verificar que:
1. Para frecuencias menores que ~p, obtenemos FdB(~ < ~p) = 0.
2. Para frecuencias mayores que ~p, obtenemos FdB(~ < ~p) = -20 log (X).
3. Para la frecuencia ~p, obtenemos FdB(~ = ~p) = -3.
Observe que la figura 5 correspondiente es el inverso aditivo del diagrama de Bode de magnitud de la función lineal. La figura 6
muestra el correspondiente diagrama de Bode asintótico de fase.
40
20
FdB (~)
0
-20
-40
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
Figura 5
0
H(~) -r/4
-r/2
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
Figura 6
Diagramas de Bode de magnitud y fase para una función cuadrática
Una función cuadrática presenta la forma:
F(S) = 1+2zS + S2.
La cantidad z es el coeficiente de amortiguamiento y es responsable de la corrección del diagrama de Bode. Al efectuar la
sustitución S = jΩ, se encuentra que la función circuital se puede expresar como:
F(j~) = 1 - Ω2 + j(2zΩ).
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::
Consecuentemente, la magnitud y la fase estan dadas por:
fdB (X) = 10 log 6(1 - X 2) 2 + (2zX 2) @,
2z X
E.
H (X) = a tan ;
1 - X2
Al igual que en el caso lineal, el diagrama de Bode de magnitud presenta dos asíntotas y una corrección a la frecuencia
característica, así:
1. Para frecuencias menores que ~p, obtenemos FdB(~ < ~p) = 0.
2. Para frecuencias mayores que ~p, obtenemos FdB(~ > ~p) = 40 log (Ω).
3. Para la frecuencia ~p, obtenemos FdB(~ = ~p) = 20 log (2z).
La corrección estará por encima del eje de frecuencias si se verifica que 2z > 1.
La corrección estará por debajo del eje de frecuencias si se verifica que 2z < 1.
La figura 7 ilustra el diagrama de Bode asintótico de magnitud correspondiente a la función cuadrática.
Para hacer la gráfica corregida a la frecuencia ~p, es conveniente usar un paquete graficador. La figura 8 ilustra el diagrama
de Bode para dos valores del coeficiente de amortiguamiento, usando el paquete Mathcad. La línea punteada corresponde
a z = 1 y la línea sólida corresponde a z = 0.1.
En cuanto al diagrama de Bode de fase, se procede de manera similar a la función lineal. Si hacemos el cambio de variable
~
, tenemos:
X=
~p
2zX m
H (X) = a tan c
.
1 - X2
Primero calculamos las tres asíntotas del diagrama, así:
1. En el intervalo 0 < ~ < 0.1~p, la asíntota es H(X) = 0.
2. En el intervalo ~ > 10~p, la asíntota es H(X) = r.
3. En el intervalo 0.1~p < ~ < 10~p , la asíntota es H (X) =
r+r
log (X) .
2
2
En la figura 9 se ilustra el diagrama asintótico de fase para la función cuadrática.
80
40
FdB (~)
0
-40
-80
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
Figura 7
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::
80
60
40
20
0
-20
-40
0.01
0.1
1
10
100
Figura 8
r
H(~)
r/2
0
0.01 ~0
0.1~0
~0
10 ~0
100 ~0
Figura 9
Supongamos que el coeficiente de amortiguamiento es mayor que la unidad; en tal caso, la función está dada por:
F (s) = 1 + 2z
s + ` s j2
.
~p
~p
s
Si hacemos el cambio de variable S =
, se tiene F(S) = 1 + 2zS + S2. Si z $ 1, la función se puede expresar como el
~p
producto de dos funciones lineales, así:
S
S
F (s) = (1 + aS) (1 + ), donde a + = 2z.
a
a
La fase de la función será la suma de las fases individuales, así:
H (X) = a tan (aX) + a tan c
Xm
.
a
Se hizo la sustitución S = jX. El valor de a está dado por a = z + z 2 - 1 ; en consecuencia, para z $ 1 la expresión
matemática para la fase es:
H (X) = a tan ^z + z2 - 1 h X + a tan ^z - z2 - 1 h X.
Evidentemente la fase es una función continua para todos los valores de la variable.
Teniendo en cuenta la identidad trigonométrica tan ^a + b h =
tan (a) + tan (b)
, se puede escribir:
1 - tan (a) tan (b)
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::
aX
H (X) = a tan >
+X
a H = a tan ; 2zX E .
1 X2
1 - X2
Se puede concluir que la expresión de arriba es continua en X = 1, al menos para z $ 1.
Veremos que si z < 1, la función deberá ser continua.
Supongamos ahora que el coeficiente de amortiguamiento es menor que la unidad z < 1. En este caso podemos expresar la
función circuital en la forma:
F(s) = 1 + 2zS + S2 = 1 + 2zS + z2S2 + (1 - z2)S2 = (1 + zS)2 + (1 - z2)S2.
En forma factorizada, queda (1 + zS + j 1 - z 2 S) (1 + zS - j 1 - z 2 S) . Haciendo el cambio de variable S = jX , resulta:
F (jX) = (1 1 - z 2 X + jzX) (1 + 1 - z 2 X + jzX) .
La fase correspondiente está dada por:
H (X) = a tan c
zX
zX
m + a tan c
m.
2
+
1
1 z X
1
1 - z2 X
A partir de la expresión anterior se llega al mismo resultado que se obtuvo para z > 1. Para evitarnos un doble trabajo en la
gráfica de la fase, usaremos la siguiente expresión que es válida para cualquier valor de z:
Z
]] a tan c 2zX 2 m
X#1
1-X
H (X) = [
]] r + a tan c 2zX 2 m X 2 1
1-X
\
La figura 10 muestra el diagrama corregido de fase para dos valores del coeficiente de amortiguamiento, usando el mismo
paquete. La línea punteada corresponde a z = 1 y la línea sólida corresponde a z = 0.1.
3.14
2.36
1.57
0.79
0
0.01
0.1
0.1
10
100
Figura 10
:: Circuitos eléctricos II — Programa de Educación Virtual —Ude@— Para ser, saber y saber hacer ::