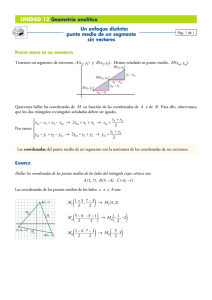
Ejercicio 1 Encuentra las coordenadas de un punto P perteneciente

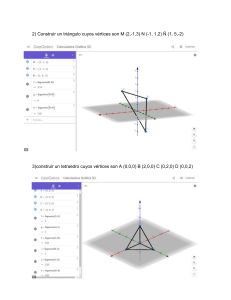
Repartido 7 - Matemática II
Liceo Nº35 - IAVA
abril 2016
Ejercicio 1
Encuentra las coordenadas de un punto P perteneciente al segmento de extremos A = (1, 5, 0) y B =
(1, −4, 9) de manera tal que AP = 49 AB.
Ejercicio 2
Encuentra las coordenadas de un punto P perteneciente al segmento de extremos A , B, C y D que
dividen al segmento de extemos P = (1, 2, 3) y Q = (6, −3, 8) en cinco partes iguales.
Ejercicio 3
Encuentra las coordenadas del baricentro del tetraedro de vértices A = (4, 6, 2), B = (2, 7, 3), C =
(3, 0, 2) y D = (−1, −1, 1).
Ejercicio 4
Sean A, B y M tres puntos diferentes del espacio que verifican la relación AB = −2AM. Sabiendo que
A = (3, −5, 1) y B = (−5, 7, 3) calcula
a) Las coordenadas del punto M.
b) El valor de k ∈ R para el que vale que MA = k.MB.
Ejercicio 5
Tres antenas A, B y C están alineadas de manera que la distancia entre B y C es el doble de la distancia
entre A y B. Conociendo las coordenadas de A = (1, 0, −2) y B = (3, 2, 1) en un cierto referencial,
halla las posibles coordenadas de C en dicho referencial.
Ejercicio 6
¿Es posible que los puntos A = (5, 1, 1), B = (3, 4, 4), C = (0, 1, 1), D = (−2, 4, 4) y E = ( 32 , 72 , 32 )
sean vértices de una pirámide? Justifica tu respuesta.
Ejercicio 7
Continuando con el ejercicio 6, halla el simétrico del punto A con respecto al punto D y el simétrico
del punto E con respecto al centro de la base de la pirámide.
Ejercicio 8
Demuestra que u + v y u − v son ortogonales sii |u| = |v|.
Ejercicio 9
Sean los vectores u = (1, 2, 3), v = (0, 3, −2) y w = (1, 1, 0).
Halla, si es posible, todos los vectores de la forma w +αu +β v que sean ortogonales simultáneamente
a u y a v.
Ejercicio 10
Prueba que si |u + v| = |u| + |v| entonces u y v son l.d.. ¿Vale el recíproco?
Diego Charbonnier
1