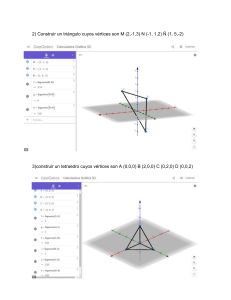
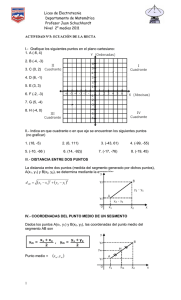
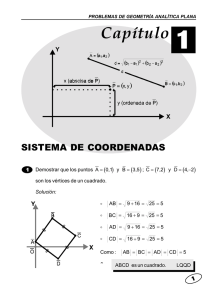
Un enfoque distinto: punto medio de un segmento sin vectores
Anuncio
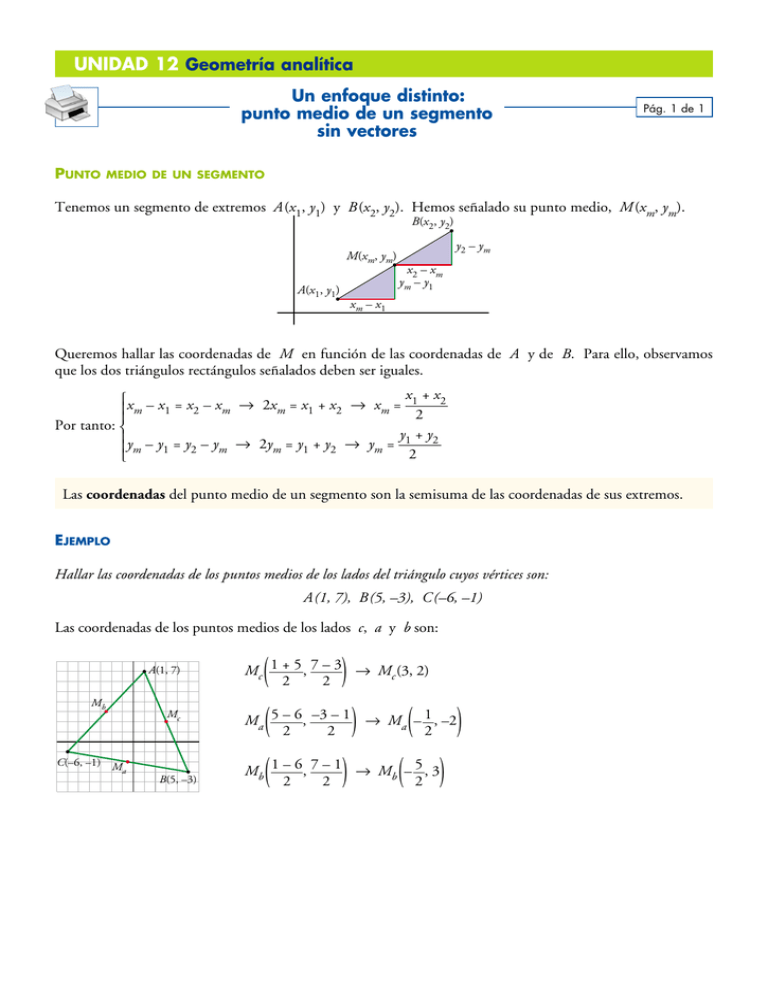
UNIDAD 12 Geometría analítica Un enfoque distinto: punto medio de un segmento sin vectores Punto Pág. 1 de 1 medio de un segmento Tenemos un segmento de extremos A (x1, y1) y B(x2, y2). Hemos señalado su punto medio, M(xm, ym). B(x2, y2) M(xm, ym) A(x1, y1) y2 – ym x2 – xm ym – y1 x m – x1 Queremos hallar las coordenadas de M en función de las coordenadas de A y de B. Para ello, observamos que los dos triángulos rectángulos señalados deben ser iguales. x1 + x2 °x – x = x – x 8 2x = x + x 8 x = — § m 1 2 m m 1 2 m 2 Por tanto: §¢ y1 + y2 §y – y = y – y 8 2y = y + y 8 y = — § m 1 2 m m 1 2 m 2 £ Las coordenadas del punto medio de un segmento son la semisuma de las coordenadas de sus extremos. Ejemplo Hallar las coordenadas de los puntos medios de los lados del triángulo cuyos vértices son: A(1, 7), B(5, –3), C(–6, –1) Las coordenadas de los puntos medios de los lados c, a y b son: A(1, 7) Mb C(–6, –1) M a Mc B(5, –3) ( ( ( ) Mc 1 + 5 , 7 – 3 8 Mc (3, 2) 2 2 ) ( ) Ma 5 – 6 , –3 – 1 8 Ma – 1 , –2 2 2 2 ) ( ) Mb 1 – 6 , 7 – 1 8 Mb – 5 , 3 2 2 2