2 - ies maestro juan maría leonet

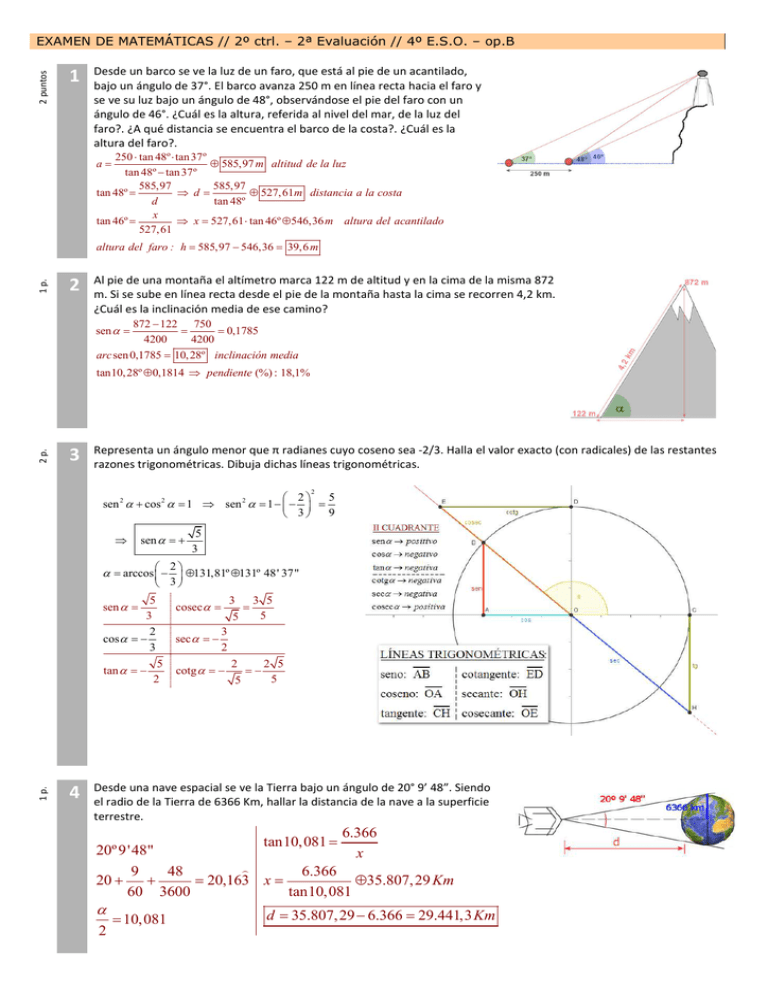
2 puntos
EXAMEN DE MATEMÁTICAS // 2º ctrl. – 2ª Evaluación // 4º E.S.O. – op.B
1
Desde un barco se ve la luz de un faro, que está al pie de un acantilado,
bajo un ángulo de 37°. El barco avanza 250 m en línea recta hacia el faro y
se ve su luz bajo un ángulo de 48°, observándose el pie del faro con un
ángulo de 46°. ¿Cuál es la altura, referida al nivel del mar, de la luz del
faro?. ¿A qué distancia se encuentra el barco de la costa?. ¿Cuál es la
altura del faro?.
250 ⋅ tan 48º ⋅ tan 37º
≈ 585,97 m altitud de la luz
tan 48º − tan 37º
585,97
585,97
tan 48º =
⇒ d=
≈ 527,61 m distancia a la costa
d
tan 48º
x
tan 46º =
⇒ x = 527,61 ⋅ tan 46º ≈ 546,36 m altura del acantilado
527,61
a=
1 p.
altura del faro : h = 585,97 − 546,36 = 39,6 m
2
Al pie de una montaña el altímetro marca 122 m de altitud y en la cima de la misma 872
m. Si se sube en línea recta desde el pie de la montaña hasta la cima se recorren 4,2 km.
¿Cuál es la inclinación media de ese camino?
872 − 122 750
=
= 0,1785
4200
4200
arc sen 0,1785 = 10, 28º inclinación media
sen α =
2 p.
tan10,28º ≈ 0,1814 ⇒ pendiente (%) : 18,1%
3
Representa un ángulo menor que π radianes cuyo coseno sea -2/3. Halla el valor exacto (con radicales) de las restantes
razones trigonométricas. Dibuja dichas líneas trigonométricas.
2
5
 2
sen 2 α + cos 2 α = 1 ⇒ sen 2 α = 1 −  −  =
9
 3
⇒
sen α = +
5
3
 2


α = arccos  −  ≈ 131,81º ≈ 131º 48' 37"
3
5
3
2
cos α = −
3
sen α =
1 p.
tan α = −
4
5
2
3 3 5
=
5
5
cosec α =
sec α = −
3
2
cotg α = −
2
2 5
=−
5
5
Desde una nave espacial se ve la Tierra bajo un ángulo de 20° 9’ 48”. Siendo
el radio de la Tierra de 6366 Km, hallar la distancia de la nave a la superficie
terrestre.
tan10,081 =
6.366
x
20º 9'48"
⌢
9
48
6.366
20 +
+
= 20,163 x =
≈ 35.807,29 Km
60 3600
tan10,081
α
2
= 10,081
d = 35.807,29 − 6.366 = 29.441,3 Km
2 p.
5
Un hombre que está situado al oeste de la antena de una emisora de radio observa
que su ángulo de elevación es de 45°. Camina 50 m hacia el sur y observa que el
ángulo de elevación es ahora de 30°. Hallar la altura de la antena.
tan 30º =
h
d
h
tan 30º
d =h 3
1 p.
d=
6
(h 3)
h2 = 1250
h = 25 2 m ≈ 35,35 m
Calcular la hipotenusa de un triángulo rectángulo, siendo el cateto b = 75 cm y la bisectriz
del ángulo agudo C = 94 cm.
75
94
cos α = 0,7978
→ α ≃ 37,07º
= 2α = 74,14º
C
1 p.
= 502 + h 2
3h 2 = 2500 + h 2
cos α =
7
2
cos74,14º =
a=
75
a
75
= 274,43 m
cos 74,14º
Calcular la altura de una torre situada en terreno horizontal, sabiendo
que con un aparato de medida colocado a 85,24 m de ella, y con una
altura de 1,15 m, se ha medido el ángulo que forma con el horizonte la
visual dirigida al punto más elevado, obteniendo un valor de 44° 26'.
⌢
26
x
= 44,43º ; tan 44, 43º =
60
85, 24
x = 85,24 ⋅ tan 44,43º ; x = 83,56
44º 26' → 44 +
h = 83,56 + 1,15 = 84,71 m