trabajo sobre cofunciones y angulos de elevacion y depresion

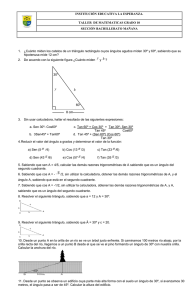
I. E. ATANASIO GIRARDOT
Matemáticas
Trabajo sobre aplicaciones de las razones trigonométricas
Grado 10° - 2015
Profesor: DIEGO JARAMILLO
Lea con atención a cada uno de los siguientes enunciados y desarrolle lo que se le pide. Debe tener en cuenta
que hay que entregar un trabajo escrito en hojas, bien ordenado y grupos de 3 personas, máximo, además es
la base para la evaluación sobre este tema
I.
Utilice las identidades fundamentales para encontrar los valores de las razones trigonométricas
que faltan para 
11
1
, Sen  
12
12
2
3
c) Sen  
, Cot  
3
13
a) Cos  
II.
Escribe la cofunción que le corresponde a cada expresión dada:
a) Cos 35 
b) Sec 65 
c) Tan 43 
d) Cot 2315'25' ' 
III.
1
11
, Sen  
12
12
1
3
d) Cos  
, Tan  
3
10
b) Cos  
e) Csc 4030' 
f) Sen 17 
Según las situaciones planteadas, realice lo que se le pide
1. Una palma proyecta una sombra de 18 m de largo. Si el ángulo que se forma desde la punta de
la sombra hasta el punto más alto de la palma es de 48°, ¿cuál es la altura de la palma?
2. Una banda transportadora de 9 metros de largo puede bajar o subir hidráulicamente para
descargar pasajeros de las aeronaves. Encuentre el ángulo que hay que levantar para llegar a
una puerta de un avión que está a 4 metros arriba de la plataforma que la sostiene.
3. Un salvavidas se encuentra en una torre a 20 m del nivel del mar, descubre que una persona
necesita de su ayuda a un ángulo de depresión de 35°. ¿A qué distancia de la base de la torre
se encuentra la persona?
4. Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del
pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste.
5. Una persona que mide 1,75 m está parada en el extremo de un muelle que sobresale 4,5 m por
encima del agua, está observando una lancha con un ángulo de depresión de 15°. ¿Cuál es la
distancia que separa la lancha de la base del muelle?
6. Un turista observa la parte más alta de un edificio de 15 m de altura, con un ángulo de
elevación de 24. Si realiza la observación con unos binoculares que sostiene a 1,75 m del
suelo, calcule la distancia aproximada entre el turista y la parte más alta del edificio.
7. Un puente levadizo mide 7.5 m de orilla a orilla, y forma un ángulo de depresión desde la
orilla, hasta un punto en la superficie del agua, de 27° (Véase fig. a). Cuando el puente está
completamente abierto forma un ángulo de 43° con la horizontal (Véase fig. b). Cuando el
puente se abre completamente, cuál es la distancia d entre el punto más alto y el agua que hay
debajo?