Cálculo del campo eléctrico debido a un segmento de línea cargada

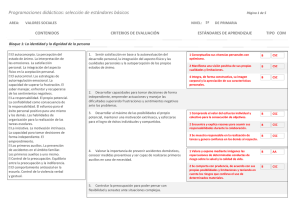
Cálculo del campo eléctrico debido a un segmento de línea cargada.
FMPR.
La figura muestra un segmento de línea con distribución líneal uniforme de carga λ y un
punto cualquiera A separado una distancia “a”del eje del segmento.
Imaginemos el segmento dividido en pequeños segmentos infinitesimales dx. La carga dq
de un segmento dx está dada por dq= λdx. La distancia “r” de un segmento en la posición x
r
hasta el punto A es r = x 2 + a 2 . La contribución dE al campo en A, debido a este
segmento está dado por:
v
r F
dq ⋅ q0
λ ⋅ dx
dq
x
a
dE =
r̂ = k
r̂ = k 2 r̂ = k 2 r̂ Como rˆ = + iˆ + ˆj
2
q0
r
r
q0 ⋅ r
r
r
r
λ ⋅ dx ⎛ x
a ⎞
dE = k 2 ⎜ + î + ˆj ⎟
r ⎠
r ⎝ r
r ⎛ k ⋅ λ ⋅ x ⋅ dx
k ⋅ λ ⋅ a ⋅ dx ˆ ⎞
dE = ⎜
î +
j⎟
3
r
r3
⎝
⎠
r
dE = +dE x î + dE y ĵ
v
Integrando E = ∫ dE x ⋅ î + ∫ dE y ⋅ ˆj
Para hallar el campo total en el punto A necesitamos sumar (integrar) las contribuciones de
todos los segmentos.
Integrando primero la componente en x.
x2
x2
x 2 x ⋅ dx
λ ⋅ x ⋅ dx
E x = ∫ dE x = ∫ k
= k ⋅ λ∫
3
x1
x1
x1
r
r3
(
Como r = x 2 + a 2
)
1/ 2
(
; r3 = x2 + a 2
Sustituyendo E x = k ⋅ λ ∫
x2
(x
)
3/ 2
;
x ⋅ dx
)
3/ 2
+ a2
Realizando un cambio de variable u = x 2 + a 2 ; du = 2 x ⋅ dx
x1
2
Por lo tanto
x2
E x = kλ ∫
x2
x1
Ex = k
⎡
⎤
λ x 2 −3 / 2
λ ⎢ u −1 / 2 ⎥
Ex = k ∫ u
⋅ du = k ⎢
⎥
2 x1
2⎢ 1 ⎥
−
⎣⎢ 2 ⎦⎥ x1
du 1
;
⋅
2 u3/ 2
[
λ
− 2u −1 / 2
2
]
x2
x1
x2
⎡ 1 ⎤
= kλ ⎢ − 1 / 2 ⎥ ;
⎣ u ⎦ x1
⎡
⎤ a
1
1
E x = kλ ⎢ 2
−
⎥×
2 1/ 2
(x 22 + a 2 )1 / 2 ⎦⎥ a
⎣⎢ ( x 1 + a )
λ
E X = k [senθ1 − senθ 2 ]
a
Integrando la componente en y
x2
x2
λ ⋅ a ⋅ dx
E y = ∫ dE y = ∫ k
x1
x1
r3
x2
x 2 a ⋅ dx
dx
E y = k ⋅ λ∫
= k ⋅ λ ⋅ a∫
3
x1
x1
r
(x 2 + a 2 )3 / 2
x
ctgθ = ; x = a ⋅ ctgθ ; dx = − a csc 2 θ ⋅ dθ
a
2
x 2 − a ⋅ csc θ ⋅ dθ
E y = k ⋅ λ ⋅ a∫
3/ 2
x1
a 2 ctg 2 θ + a 2
(
x2
E y = k ⋅ λ ⋅ a∫ −
x1
)
a ⋅ csc 2 θ ⋅ dθ
(
)
a 3 ctg 2 θ + 1
3/ 2
Recordando que (sen 2 θ + cos 2 θ = 1)(
1
);
sen 2 θ
sen 2 θ cos 2 θ
1
+
=
; 1 + cot 2 θ = csc 2 θ;
2
2
2
sen θ sen θ sen θ
x2
a ⋅ csc 2 θ ⋅ dθ
E y = k ⋅ λ ⋅ a∫ −
3/ 2
x1
a 3 csc 2 θ
(
x2
E y = k ⋅ λ ⋅ a∫ −
x1
Ey = k ⋅λ ⋅
a
a2
∫
x2
x1
)
x2
csc θ ⋅ dθ
dθ
=k ⋅ λ ⋅ a ∫ − 2
2
3
x1
a (csc θ)
a (csc θ)
2
− senθ ⋅ dθ
1
λ x2
x
− senθ ⋅ dθ = k ⋅ λ ⋅ [cos θ]x12
∫
a x1
a
1
E Y = k ⋅ λ ⋅ [cos θ 2 − cos θ1 ]
a
Ey = k ⋅