x xxx f ∫ ff fff ∫ ∫− fh h fh h ∫− ∫ xfhfff

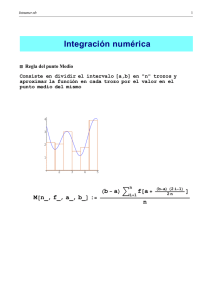
Integracion Numerica
1
Integración numérica
∫
La evaluación de una integral definida
b
a
f ( x)dx en forma explicita es a veces muy difícil; o
particularmente imposible. En tales casos puede hacerse una aproximación numérica tal como las que se
mencionan a continuación:
Regla de trapecios.
Una posible forma de resolver el problema es aproximando localmente la funcion f(x) por otra g(x) mas
simple de integrar.
La regla de los trapecios se aproxima a f(x)con segmentos de recta y entonces:
∫
x1
x0
f ( x)dx ≅
[
1
( − ) f ( x0) + f ( x1)
2 x1 x0
]
Esta aproximación puede generalizarse para un intervalo [x0, xh]. Considerando abscisas con
espaciamiento uniforme, Xi = Xi-1 + h para las que se tiene valores de la función fi=f(xi), puede hacerse
interpolaciones lineales en cada sub-intervalo [Xi, Xi+1 ] para obtener:
∫
xn
x0
f ( x)dx =
h
2
(f
0
+2
f
1
+2
f
2
+ ... + 2
f
n −1
+
f
n
)
el error de truncamiento puede estimarse mas fácilmente considerando primero un sub-intervalo,
v..g. int[-h/2, h/2], para el cual siendo h pequeño:
f(x) = f(0) + xf’(0) + ½ x² f”(0) + 1/6 x3 f”’(0) + 1/24 x4 fiv(0)+….+
∫
h/2
−h / 2
f ( x)dx =hf (0) + h
2
4
f " ( 0) + h f
24
1920
iv
(0) + ...
y tambien: f(±h/2) = f0 ± h/2 f’(0) ± h/8 f”(0) ± h/48 f’”(0) ± h/384 fiv(0) ±...
por lo tanto,
3
∫
h/2
−h / 2
4
h
f ( x)dx = [ f (h / 2) + f (− h / 2)] − h f ' ' ' (0) − h
2
12
480
f
iv
( 0)
Si h es pequeño el error local de truncamiento es de O(h3). Sin embargo para integrar etre limites a y b se
requiere (b-a)/h subintervalos (este numero es inversamente proporcional a h) y el error global es entonces
del O(h²).
Regla de Simpson.
La aproximación local se hace interpolando parabolas de 2do grado, considerando puntos con abscisas
uniformemente espaciadas:
∫
x2
x0
h
f ( x)dx =
3
(f
f ) − h90 f ( x ) + ...
5
0
+4
f
1
+
iv
2
1
y en general considerando un numero par de subintervalos:
Integracion Numerica
∫
xn
x0
f ( x)dx =
h
3
(f
0
2
+4
f
1
+2
f
2
+4
f
3
+ ... + 2
f
n−2
+4
f
n −1
+
f
) + O (h )
n
n
Esta formula es exacta cuando f(x) es un polinomio de grado 3.
Las formulas de los trapecios y de Simpson corresponden al grupo de formulas de Newton-Cotes de
intervalo cerrado. Algunas formulas de este grupo son:
x 3 f ( x )dx = 3h ( + 3 + 3 + ) + O( 3 ) (Regla de Simpson de los 3/8)
f
f1 f 2 f 3
h
0
8 0
∫x
4
x 4 f ( x )dx = 2h (
+ 32 f 1 + 12 f 2 + 32 f 3 + 7 f 4 ) + O(h ) (Bode)
7
f
0
0
45
∫x
También pueden obtenerse fórmulas que utilizan puntos uniformemente espaciados pero no
incluyen valores de la funcion en uno o dos limites de la integral. Estas son formulas de NewtonCotes de intervalo abierto:
x 3 f ( x )dx = 3h ( + ) + O( 3 )
f f
h
0
2 1 2
∫x
x 4f ( x )dx = 4h (2 − + 2 ) + O( 5 )
f1 f 2 f 3
h
0
3
∫x
Extrapolación de Richarson y el método de Romberg
b
∫a f ( x )dx
Si T(h) es la aproximación de
obtenida de la aplicación de la regla de trapezoidal con
intervalo “h”, puede escribirse:
b
2
4
6
T(h) = ∫a f ( x )dx + a1h + a2 h + a3 h + ...
b
2
4
6
T(2h) = ∫a f ( x )dx + a1(2h) + a2 (2 h) + a3 (2 h) + ... y entonces:
b
4T(h) − T(2h)
4
6
= ∫a f ( x )dx + b2 h + b3 h
3
es decir que 1/3(4T(h)-T(2h)) es una aproximación a
b
∫a f ( x )dx con un error de truncamiento de O(h )
4
menor que T(h) ó T(2h). En forma simila, para la regla de Simpson:
b
4
6
8
S(h) = ∫a f ( x )dx + b2 h + b3 h + b4 h + ...
b
4
6
8
s(2h) = ∫a f ( x )dx + b2 (2h) + b3 (2 h) + b4 (2 h) + ... y entonces:
4
2
S(h) − S(2h)
4
2
−1
b
6
8
= ∫a f ( x )dx + c 3 h + c 4 h
Es una mejor aproximación a la integral, con un error global de O(h6)