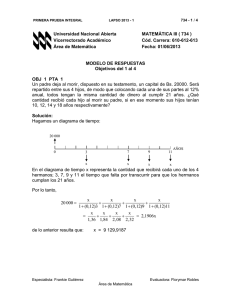
Demuestre que a.- div(λ r) = 3λ λ IR, r (x,y,z) ∈ = r r b

Segunda Parcial
Lapso 2010-2
751-758 – 1/4
Universidad Nacional Abierta
Cálculo III (751)- Cálculo Vectorial(758)
Vicerrectorado Académico
Cód. Carrera: 508 - 126
Área De Matemática
Fecha 22/01/11
MODELO DE RESPUESTAS
Objetivos 5, 6, 7 y 8.
OBJ 5 PTA 1
Demuestre que
r
r
a.- div(λ r) = 3λ λ ∈ IR, r = (x, y, z)
r
r
r
b.- div(r n r) = (n + 3) r n r = (x, y, z), r = | r |
r
r
c.- div( ϕ(r) r) = 3 ϕ(r) + r ϕ′(r) donde ϕ es campo escalar, r = (x, y, z),
r
r =|r|
Solución:
Ver Ejercicio propuesto n° 4 de la sección 86 del libro Matemática IV (735), tomo I.
OBJ 6 PTA 2
r
Sea F :U⊂ IR3 →IR3 un campo vectorial definido por
r
⎛
⎞
x2
x2
F(x, y, z) = ⎜ 2 x ln( y z) − 5 y e x ,
− 5e x ,
+ 2z⎟
y
z
⎝
⎠
3
donde U = {x, y, z)∈IR / x > 0, y > 0, z > 0}. Sea C una curva que une los puntos A = (2, 2, 1) y
r
B = (3, 1, e). Calcule ∫ F ⋅ dr .
C
Solución:
Veamos si el campo es conservativo. En efecto
rot( F ) =
y
i
j
k
∂
∂x
∂
∂y
⎛ ∂R ∂Q ∂P ∂R ∂Q ∂P ⎞
∂
=⎜
−
,
−
,
−
⎟
∂z
⎝ ∂y ∂z ∂z ∂x ∂x ∂y ⎠
P
Q
R
∂P
∂Q
= − 5e x + 2x =
y ∂x
∂y
∂ P 2x
∂R
=
=
z
∂z
∂x
∂Q
∂R
=0=
∂z
∂y
Elaborado por: Belkys Escobar
Área de Matemática
Segunda Parcial
Lapso 2010-2
751-758 – 2/4
r
r
Como U es un conjunto abierto y convexo y rot F = 0, entonces F es conservativo.
Luego, podemos calcular la integral de línea usando un camino C′ que una los puntos A y B o también
podemos calcular una función potencial f y usar el teorema fundamental para integrales de línea. En
este caso vamos a calcular la integral usando la función potencial f.
Como ∇f = F entonces fx = P, fy = Q, y fz = R
f x = 2 x ln(y z) − 5 y e x
fy =
x2
− 5e x
y
fz =
x2
+ 2z
z
f x = 2 x ln(y z) − 5 y e x ⇒ f (x, y, z) = ∫ (2x ln( yz) − 5ye x )dx = x 2 ln( yz) − 5ye x + K(y, z)
derivando la expresión anterior respecto de la variable y e igualando a la segunda ecuación, resulta:
∂ K( y, z)
x2
∂ K( y, z)
x2
=0
− 5e x +
=
− 5e x ⇒
y
y
∂y
∂y
con lo que K solo podría ser una función de z, K = K(z). Por lo tanto
f (x, y, z) = x 2 ln( yz) − 5ye x + K(z)
Para determinar K derivamos respecto de la variable z e igualando a la tercera ecuación, resulta:
x2
x2
+ 2 z ⇒ K ′(z) = 2z
+ K ′(z) =
z
z
con lo cual K(z) = z2 + k1. Finalmente
f (x, y, z) = x 2 ln(yz) − 5ye x + z 2 + k1
luego
r
3
2
F
∫ ⋅ dr = f(B) − f(A) = 8 − 5e + 11e − 4ln(2) ≈ − 13,9207.
C
OBJ 7 PTA 3
Sea el sólido Q determinado por las desigualdades 1 ≤ z ≤ 5 − x2 − y2 ; 1 ≤ x2 + y2 ≤ 2, suponiendo que
la densidad en el punto P(x, y, z) es tres veces la distancia de P al plano XY, encuentre la masa de Q.
Solución:
La masa del solido viene dada por
M = ∫∫∫ f (x, y, z) dx dy dz
Q
donde f es la función densidad que según el enunciado del problema estaría definido por
f(x, y, z) = 3| z |
Elaborado por: Belkys Escobar
Área de Matemática
Segunda Parcial
Lapso 2010-2
751-758 – 3/4
pero z ≥ 1 lo que implica que
f(x, y, z) = 3z
Usando coordenadas cilíndricas x = rcos(θ), y = rsen(θ), z = z, el sólido Q puede ser descrito por
1 ≤ z ≤ 5 − r2 ; 0 ≤ θ ≤ 2π ; 1 ≤ r ≤ 2
luego
2 π 2 5 − r2
M = ∫∫∫ f (x, y, z) dx dy dz =
∫∫ ∫
Q
3
=
2
2π 2
∫∫
0 1
0 1
3z r d z d r d θ
1
3
(24 r − 10 r + r ) d r d θ =
2
3
5
2π
∫ 9d θ = 27 π
0
por lo tanto la masa de Q es de 27π (unidades de masa).
OBJ 8 PTA 4
Sean u, v : IR2 →IR dos campos esclares continuamente diferenciable, D = {(x,y)∈IR2 / x2 + y2 ≤ 1}.
Calcule el valor de la integral doble
⎡⎛ ∂ u ∂ u ⎞
⎛∂v ∂v⎞ ⎤
v
−
+
−
⎢
⎜
⎟
⎜
⎟ u⎥ d x d y
∫∫D ⎣⎝ ∂ x ∂ y ⎠
⎝∂x ∂y⎠ ⎦
si se sabe que sobre la frontera de D se tiene que u(x,y) = 2 y v(x,y) = x
Solución:
Observemos que
⎛∂u ∂u ⎞
⎛∂v ∂v⎞
∂ (u v) ∂ (u v)
−
−
−
⎜
⎟v + ⎜
⎟u =
∂x
∂y
⎝∂x ∂y⎠
⎝∂x ∂y⎠
de aquí que podemos definir las funciones P y Q como
P(x, y) = Q(x, y) = u v
Estas funciones así definidas son continuas con primera derivas parciales continuas en un conjunto
abierto U⊂ IR2.
Sea C la frontera de D, es decir, C = { (x,y)∈IR2 / x2 + y2 = 1}, la cual es una curva regular a trozos
cerrada y simple.
Entonces por lo anteriormente expuesto podemos aplicar el teorema de Green-Riemann, esto es
⎛ ∂Q
∂P⎞
∫ P d x + Q d y = ∫∫ ⎝⎜ ∂ x − ∂ y ⎠⎟
C
D
Luego
∫∫
D
⎡⎛ ∂ u ∂ u ⎞
⎛∂v ∂v⎞ ⎤
−
−
⎢⎜
⎟v + ⎜
⎟ u⎥ d x d y =
⎝∂x ∂y⎠ ⎦
⎣⎝ ∂ x ∂ y ⎠
∫ Pd x + Qd y
C
Pero C es la frontera de D, en consecuencia u(x,y) = 2 y v(x,y) = x para todo (x, y) ∈C.
Así
∫ P d x + Q d y = ∫ 2x d x + 2x d y
C
C
Elaborado por: Belkys Escobar
Área de Matemática
Segunda Parcial
Lapso 2010-2
751-758 – 4/4
Ahora, parametricemos la curva C como sigue
x = cos(t) , y = sen(t) con 0 ≤ t ≤ 2π
entonces
∫ 2x d x + 2x d y =
C
2π
∫ [2 cos(t)( −sen(t) + 2cos(t) cos(t)] d t = 2π
0
en conclusión
∫∫
D
⎡⎛ ∂ u ∂ u ⎞
⎛∂v ∂v⎞ ⎤
−
−
⎢⎜
⎟v + ⎜
⎟ u ⎥ d x d y = 2π.
⎝∂x ∂y⎠ ⎦
⎣⎝ ∂ x ∂ y ⎠
FIN DEL MODELO
Elaborado por: Belkys Escobar
Área de Matemática