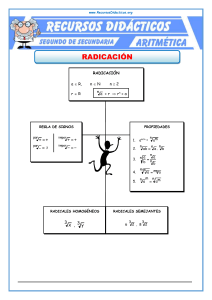
mente. respectiva 10- x,2 7 5, es subradical y 3,4,2 índices de

Universidad de Concepción
Facultad de Ciencias Veterinaria
Nivelación de Competencias en Matemática (2012)
Unidad-4: Radicales
(*)
n
Radical. Es una expresión de la forma: b que representa la raíz enésima principal de b.
El entero positivo n es el índice u orden del radical, b es el subradical.
5, 4 7 x 3  2 y 2 ,
3
x - 10 , son radicales de índices 3,4,2
y subradical es 5, 7 x 3  2 y 2 , x - 10 respectiva mente.
Propiedades de los Radicales. Son las mismas que corresponden a las potencias, ya que
n
1
n
a  a . A continuación se exponen las propiedades utilizadas con más frecuencia
Propiedades
Ejemplos
( b)  b
n
ab  n a n b
n
a
a
n
n
b0
b
b
m
n
a  (n a ) m
n
a)
b)
c)
d)
m n
e)
n
a  mn a
(3 6 ) 3  6
3
54  3 27  2  3 27  3 2  33 2
5
5
5
5
5
5
5

32
2
32
3
27 4  (3 27 ) 4  34
4
3
2  12 2
Estas propiedades las utilizaremos para simplificar radicales y para efectuar con ellas las
diversas operaciones algebraicas. No se debe olvidar que si m y n son números pares, los
subradicales a y b deben ser números NO NEGATIVOS.
Si observas con atención las propiedades anteriores no existe ninguna que permita
justificar la siguiente expresión:
n
a n  a, ¿Qué sucede si a  -3 y n  4?.
n
1) Simplificación. Se dice que el radical simple a esta simplificado cuando
satisface las siguientes condiciones:
a) El radical no contiene factores afectados de exponentes
mayores que el
índice n del radical. Ejemplo
3
8a 5  3 2 3 a 3 a 2 Propd. de las potencias
 3 2 3 a 3  3 a 2 Propiedad (b)
 2a 3 a 2
b) El subradical no contiene fracciones. Ejemplo:
27
27
32  3


2
2
2
3 3
2 3



6
2
2
2
(*) En nuestra cultura por lo general utilizamos el símbolo √ , para simbolizar
números reales que no podemos representarlos por nuestros dígitos (0 al 9), así
es un número real que podemos representarlo de manera
√
APROXIMADA con nuestros dígitos al decimal(racional) 5.73205081
1
El índice del radical es el menor posible. Ejemplo:
27  3  3
3
6
6
3
6
1
2
3  3
2) Adición y Sustracción: Se dice que dos radicales son SEMEJANTES si después de
que han sido simplificados constan del mismo subradical y el mismo índice.
Por ejemplo, 3 7 y - 2 7 son radicales semejantes. La suma de radicales
semejantes se efectúa como la de términos semejantes.
4
4
4 2  2 18  3 32  50 
 4 2  2 2  9  3 16  2  25  2 
 4 2  6 2  12 2  5 2  5 2
3) Multiplicación y división. Para multiplicar dos radicales primero se reducen al
mismo índice, en caso de que sea necesario, y luego se aplica la propiedad (b).
Ejemplo
(a) Al multiplicar
3
2 por , 3, se busca el M.C.M. de los índices 3 y 2, que es 6 por lo
que se convertirá cada radical al índice 6. Así resulta :
1
3
2
6
22 2 6 4
3
3
6
1
2
3  3  3  6 27
3
2  2  6 4  6 27
 6 4  27  6 108
(b) Multiplicación de expresiones, con dos o más términos se efectúa igual que
con expresiones algebraicas. Ejemplo:
(3 x  2 y )  (2 x  3 y ) 
 6 x  4 xy  9 xy  6 y 
 6 x  5 xy  6 y
(c) Para dividir un radical por otro se reducen, si es necesario, al mismo índice
y luego se aplica la propiedad c.
Ejemplo 1
Ejemplo 2
10
10

 5
2
2
3
3 6 27 6

 3
3 6 9
4) Racionalización del denominador: En general racionalizar el denominador de una
fracción dada significa TRANSFORMAR esa fracción en otra equivalente cuyo
denominador posee raíces exactas.
a) Racionalizar un monomio
Ejemplo:
3
3
2
3 2
3




2
2
2
2
2
2 ( 2)
(recuerda que ( 2 ) 2  2
2
En general Racionalizar un monomio con
Debemos amplificar por
Ejemplo:
n
n
(....) , n  2
(....) n 1
4
4 3 2 2 43 4 4 3 4
 3 3 2  3 3 
 23 4
3
2
2
2
2
2
b) Racionalizar un Binomio.
Ejemplo:
6
13  10
En este caso la complicaci ón está en el binomio
13  10 , que al ser multiplica do por 13  10
tenemos ( 13  10 )  ( 13  10 )  ( 13 ) 2  ( 10 ) 2 
 13  10  3
luego
6
6
13  10 6( 13  10 )




3
13  10
13  10
13  10
 2( 13  10 )
3
EJERCICIOS
Encuentre la longitud del lado de un cuadrado de área 6.25 cm2.
Si el área de un cuadrado se duplica, ¿Se duplica la longitud del lado?.
Para duplicar la longitud del lado de un cuadrado, ¿cuánto debe aumentar su área?
Una mesa de cubierta rectangular con dimensiones 90 y 160 cm se quiere transformar
en otra de cubierta cuadrada,¿Cuánto deberán variarse sus dimensiones para mantener
constante su superficie?.
5) Dado el cubo:
1)
2)
3)
4)
a) Calcule la longitud de la arista si su volumen es 2700
b) Calcule el área de una cara si su volumen es:
i)
12 cm3.
ii)
V cm3.
cm3.
c)
Encuentre la longitud de la arista si su volumen es igual
depósito rectangular de dimensiones 24, 25 y 45 cm.
al de un
6.- Para pintar un estanque de forma cúbica, cuya capacidad es de 24000 lt se ocuparon 3,5
lt de pintura. ¿Cuánta pintura se necesitará para pintar otro estanque con la misma forma
cuya capacidad es de 48000 lt?.
7.- ¿Cuál de los siguientes procedimientos permite(n) construir con regla y compás el
número
5 ?.
I) Como la hipotenusa de un triángulo rectángulo de catetos 2 y 1.
II) Como la media proporcional geométrica entre 5 y 1.
III) Como el cateto de un triángulo rectángulo de hipotenusa 3 y
cateto conocido 2.
8.- Establezca el orden creciente entre los números
9.- Si
10.-
(x 3 )
2
3
22
12
a  2, b  3 2, c 
4.
 64
=?
11.- Reduzca a una expresión radical más simple:
a ) (7 3 4ab )
b) 64 x 7 y  6
c ) n a n b 2 n c 3 n 1 c m  2
d)
x  25
x 5
e) 2a a 2  6a  9
4
12.- Racionalizar el denominador de las siguientes expresiones
2
3
3
b) 3
6
a)
y
)
2x
a-b
d)
ab
4 xy 2
e)
3
2 xy 2
c) 3x( 4
13.- Suma y resta radicales semejantes
a) 18  50  72
b) 4 75  3
4
 2 48
3
c) 3  3 81  27  53 3
d ) 3  3 81  27  5 3
e) 2a 3 27 x 3 y  3b3 8 x 3 y  6c 3  x 3 y
14.- ¿ Explique la diferencia entre
x2  9 y x  9 .
2
2
b) A=( B ) y C= B ?.
a)
5