Ecuaciones de Curvas en Coordenadas Polares

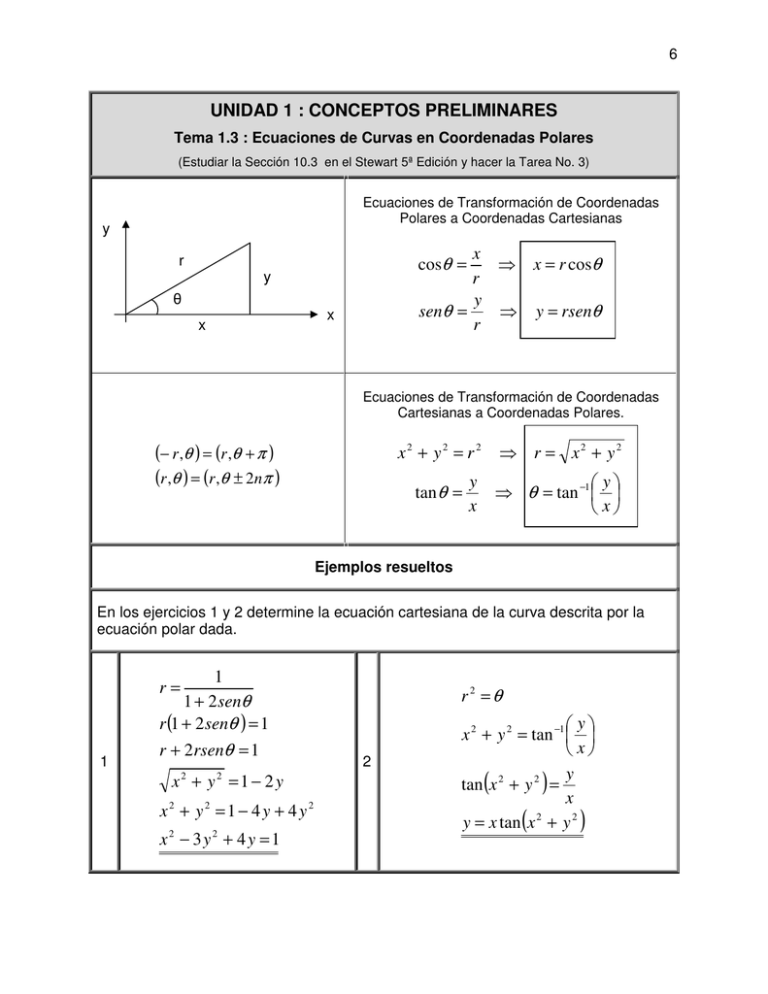
6
UNIDAD 1 : CONCEPTOS PRELIMINARES
Tema 1.3 : Ecuaciones de Curvas en Coordenadas Polares
(Estudiar la Sección 10.3 en el Stewart 5ª Edición y hacer la Tarea No. 3)
Ecuaciones de Transformación de Coordenadas
Polares a Coordenadas Cartesianas
y
x
⇒ x = r cosθ
r
y
senθ =
⇒ y = rsenθ
r
r
cosθ =
y
θ
x
x
Ecuaciones de Transformación de Coordenadas
Cartesianas a Coordenadas Polares.
(− r ,θ ) = (r ,θ + π )
(r ,θ ) = (r ,θ ± 2nπ )
x2 + y2 = r 2
⇒ r = x2 + y2
y
x
 y
⇒ θ = tan −1  
 x
tan θ =
Ejemplos resueltos
En los ejercicios 1 y 2 determine la ecuación cartesiana de la curva descrita por la
ecuación polar dada.
1
1 + 2 senθ
r (1 + 2 senθ ) = 1
r=
1
r + 2rsenθ = 1
2
2
x + y =1 − 2y
x2 + y2 = 1 − 4 y + 4 y2
x2 − 3y2 + 4 y = 1
r2 =θ
2
 y
x 2 + y 2 = tan −1  
 x
y
tan (x 2 + y 2 ) =
x
2
y = x tan (x + y 2 )
7
En los ejercicios 3 y 4, determine una ecuación polar de la curva representada por la
ecuación cartesiana dada.
y = 2x − 1
rsenθ = 2r cosθ − 1
x2 = 4 y
2r cosθ − rsenθ = 1
r 2 cos 2 θ = 4rsenθ
4 senθ
r=
cos 2 θ
r (2 cosθ − senθ ) = 1
r=
3
1
2 cosθ − senθ
4
1
cosθ
r=
2 cosθ − senθ
cosθ
secθ
r=
2 − tanθ
r=4
senθ 1
cosθ cosθ
r = 4 tanθ secθ
En los ejercicios 5 y 6 determine la ecuación cartesiana y dibújela
r = 2 senθ + 2 cosθ
r = 4 cosθ
 y x
r = 2 + 
r r
r 2 = 2( x + y )
5
r 2 = 4r cosθ
x2 + y 2 = 4x
x 2 + y 2 = 2x + 2 y
6
x 2 − 2x + 1 + y 2 − 2 y + 1 = 2
x2 − 4x + 4 + y 2 = 4
(x − 2)2 + y 2 = 4
(x − 1)2 + ( y − 1)2 = 2
en un círculo con centro
en C (1,1) y radio r =
2
en un círculo con centro
en C (2,0 ) y radio r = 2
8
Resumen de Ecuaciones de Curvas en Coordenadas Polares
Coordenadas Polares (Stewart 5ª Ed Secciones 10.3 y 10.4)
Ecuaciones de
Transformación de
Coordenadas
r = x2 + y2
x = r cos(θ )
y = rsen(θ )
 y
 x
θ = tan −1  
 dy 
dr
 
(
)
(
)
θ
θ
r
sen
cos
+
θ
d
  (r0 ,θ0 )
 dy 
dθ
=
=
 
dr
 dx  ( x0 , y0 )  dx 
− rsen(θ ) + cos(θ )
 
dθ
 dθ  (r0 ,θ0 )
Pendiente en
un punto (x0,y0)
Area debajo de un
segmento de la curva
r = f (θ )
∫
θ2
A = dA =
θ1
∫
θ2
θ1
1 2
r dθ =
2
∫
θ2
θ1
1
[ f (θ )]2 dθ
2
x = r cos(θ ) = f (θ ) cos(θ ); y = rsen(θ ) = f (θ )sen(θ )
dx dr
dy dr
cos(θ ) − rsen(θ );
=
=
sen(θ ) + r cos(θ )
dθ dθ
dθ dθ
2
Diferencial de Arco
2
 dx   dy 

 +
 =
 dθ   dθ 
2
2
2
 dx   dy 
ds = 
 +
 ⋅ dθ
 dθ   dθ 
dr
 dr 
2
cos(θ )sen(θ ) + r 2 sen 2 (θ ) +

 cos (θ ) − 2r
dθ
 dθ 
2
dr
 dr 
2
cos(θ )sen(θ ) + r 2 cos 2 (θ )

 sen (θ ) + 2r
dθ
 dθ 
2
 dr 
2
=
 +r
 dθ 
2
 dr 
2
∴ ds = 
 + r ⋅ dθ
 dθ 
Longitud de Arco de un
segmento de la curva
θ1 ≤ θ ≤ θ 2
s=
∫
θ2
θ1
2
 dr 
2

 + r ⋅ dθ
 dθ 
9
Ma-817 : MATEMÁTICAS III PARA INGENIERIA
Tarea No. 3 : Coordenadas Polares
En los problemas 1 y 2, dibuje la región en el plano formada por los puntos cuyas
coordenadas polares satisfacen las condiciones dadas.
1
0≤r ≤2 ;
π
2
≤θ ≤ π
2≤r ≤3 ;
2
5π
7π
≤θ ≤
3
3
En los problemas 3 y 4 determine la ecuación cartesiana de la curva descrita por la
ecuación polar dada.
3
r = 3senθ
r 2 = sen(2θ )
4
En los problemas 5 y 6, determine una ecuación polar de la curva representada por la
ecuación cartesiana dada.
5
x 2 + y 2 = 25
2 xy = 1
6
En los problemas 7 y 8 determine la ecuación cartesiana y dibújela
7
r = −2 senθ
r = cscθ
8
2
3  3

R3 : x +  y −  =  
2  2

2
(
R4 : x 2 + y 2
R5 : r = 5
)
2
= 2 xy
R6 : r 2 = csc(2θ )
R7 : x 2 + ( y + 1)2 = 1
R8 : y = 1
2