Pruebas para una media con muestra grande

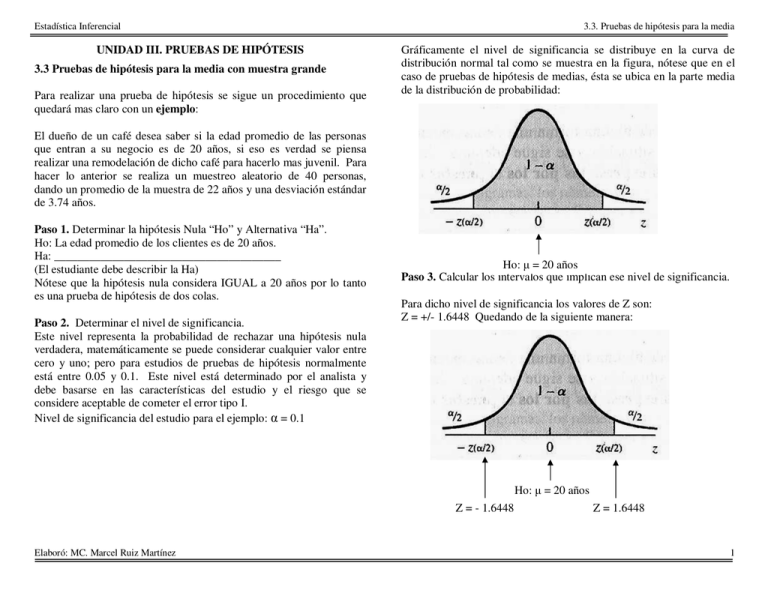
Estadística Inferencial
UNIDAD III. PRUEBAS DE HIPÓTESIS
3.3 Pruebas de hipótesis para la media con muestra grande
Para realizar una prueba de hipótesis se sigue un procedimiento que
quedará mas claro con un ejemplo:
3.3. Pruebas de hipótesis para la media
Gráficamente el nivel de significancia se distribuye en la curva de
distribución normal tal como se muestra en la figura, nótese que en el
caso de pruebas de hipótesis de medias, ésta se ubica en la parte media
de la distribución de probabilidad:
El dueño de un café desea saber si la edad promedio de las personas
que entran a su negocio es de 20 años, si eso es verdad se piensa
realizar una remodelación de dicho café para hacerlo mas juvenil. Para
hacer lo anterior se realiza un muestreo aleatorio de 40 personas,
dando un promedio de la muestra de 22 años y una desviación estándar
de 3.74 años.
Paso 1. Determinar la hipótesis Nula “Ho” y Alternativa “Ha”.
Ho: La edad promedio de los clientes es de 20 años.
Ha: _______________________________________
(El estudiante debe describir la Ha)
Nótese que la hipótesis nula considera IGUAL a 20 años por lo tanto
es una prueba de hipótesis de dos colas.
Paso 2. Determinar el nivel de significancia.
Este nivel representa la probabilidad de rechazar una hipótesis nula
verdadera, matemáticamente se puede considerar cualquier valor entre
cero y uno; pero para estudios de pruebas de hipótesis normalmente
está entre 0.05 y 0.1. Este nivel está determinado por el analista y
debe basarse en las características del estudio y el riesgo que se
considere aceptable de cometer el error tipo I.
Nivel de significancia del estudio para el ejemplo: α = 0.1
Ho: µ = 20 años
Paso 3. Calcular los intervalos que implican ese nivel de significancia.
Para dicho nivel de significancia los valores de Z son:
Z = +/- 1.6448 Quedando de la siguiente manera:
Ho: µ = 20 años
Z = - 1.6448
Elaboró: MC. Marcel Ruiz Martínez
Z = 1.6448
1
Estadística Inferencial
Paso 4. Calcular el “estadístico” de la prueba.
3.3. Pruebas de hipótesis para la media
Paso 5. Determinar si el estadístico cae dentro de la región que hace la
Hipótesis nula verdadera.
El estadístico Z se calcula de la siguiente manera:
σx =
z=
σ
n
x−µ
Z = 3.38
Se calcula la siguiente desviación estándar
Se calcula el valor de Z tipificado
σx
µ
Promedio considerado por la hipótesis nula.
x
Media de la muestra tomada.
Desviación estándar de la muestra.
Número de elementos muestreados.
Desviación estándar tipificada.
Valor de Z tipificado
σ
n
σx
z
σx =
z=
σ
n
x−µ
σx
=
3.74
= 0.5913
40
=
22 − 20
= 3.38
0.5913
Ho: µ = 20 años
Z = - 1.6448
Z = 1.6448
Como podrá notarse, el estadístico esta fuera de la región que hace
verdadera la hipótesis nula.
Paso 6. Aceptar o rechazar la hipótesis nula.
En este caso como el estadístico de la prueba cae fuera de la región que
hace verdadera la hipótesis nula, se rechaza y se toma como verdadera
la hipótesis alternativa:
Ho: La edad promedio de los clientes es de 20 años. (FALSO)
Ha: La edad promedio de los clientes No es de 20 años (VERDAD)
Elaboró: MC. Marcel Ruiz Martínez
2
Estadística Inferencial
Pruebas de una cola.
Para realizar pruebas de una cola auto estudie las páginas de la 300 a la
304 de la referencia:
Walpole, R. E. (1999). Probabilidad y estadística para ingenieros .
Mexico DF: Prentice Hall.
Disponible en la siguiente liga:
http://books.google.com.mx/books?id=Melpe80mYOIC&lpg=PP1&pg=PR2#v=onepage&q=&f=false
Realice ahora el siguiente ejercicio:
3.3. Pruebas de hipótesis para la media
Proveedor de focos. Una empresa de fabricación de focos desea
venderle al gobierno del estado; y para concursar con el resto de las
compañías asegura que la vida media es de al menos 500 horas; si se
toma una muestra de 50 focos y se les mide su vida media, siendo ésta
de 480 horas; si la desviación estándar en la prueba fue de 4 horas;
¿será cierta la afirmación del proveedor dados los datos indicados en la
prueba? determine lo siguiente:
a) Defina la hipótesis nula y alternativa
b) Realice la prueba de hipótesis con un nivel de significancia de
alfa = 0.1
Dueño de un café. El dueño de un café desea saber si la edad
promedio de las personas que entran a su negocio es menor o igual a
20 años, si eso es verdad se piensa realizar una remodelación de dicho
café para hacerlo mas juvenil. Para hacer lo anterior se realiza un
muestreo aleatorio de 40 personas, dando un promedio de la muestra
de 22 años y una desviación estándar de 3.74 años.
Realice la prueba de hipótesis para determinar si las personas que
entran al negocio tienen una edad igual o menor a 20 años con un nivel
de significancia de: alfa = 0.1
Elaboró: MC. Marcel Ruiz Martínez
3
Estadística Inferencial
Actividad 3.2. Problemas de hipótesis para la media.
Problema 1. Se está estudiando colocar un negocio en una zona
turística, dicho local tendrá éxito si el promedio de compras diario es
de $1,000 pesos o más.
Se decide abrir el negocio en un periodo de prueba por 40 días, en los
cuales se tienen ingresos diarios de $950 pesos con una desviación
estándar de $9 pesos. (Suponga que el producto no es estacional y se
puede muestrear de forma representativa 40 días seguidos).
Se pide lo siguiente:
a) Redacte la hipótesis nula y alternativa ¿Será correcto analizar
el problema como una o como dos colas?
b) Con un nivel de significancia de 0.1 determine la veracidad
para la hipótesis nula Ho: El promedio diario de ventas del
negocio es de $1000.
3.3. Pruebas de hipótesis para la media
Elabore una PRÁCTICA DE EJERCICIOS de este trabajo (INDIVIDUAL),
las
rúbricas
se
indican
en
la
liga
siguiente:
http://marcelrzm.comxa.com/Rubricas/Rubricas.htm
SIN EL PROCEDIMIENTO LA ACTIVIDAD NO ES VÁLIDA
Puede enviar el documento final por correo electrónico a las siguientes
direcciones:
[email protected];
[email protected];
[email protected] y [email protected]
No olvide enviarse copia a sí mismo del correo que envía, si usa Outlook
solicite confirmación de entrega y de lectura.
Problema 2. La cantidad de huéspedes que debe a un hotel para que
éste sea rentable debe ser en promedio de 200 al mes (o más). Se
estudiaron hoteles similares en la zona, registrando los 365 días del
año se detectó que tienen una demanda promedio de 195 personas al
mes aproximadamente, con una desviación estándar de 5 personas.
Se pide lo siguiente:
a) Redacte la hipótesis nula y alternativa ¿Será correcto analizar
el problema como una o como dos colas?
b) Con un nivel de significancia de 0.02 determine la veracidad
para la hipótesis nula Ho: El promedio diario de personas que
se hospedarán en el hotel es de 200 al mes.
Problema 3. Una empresa contratista asegura que la duración promedio de
los indicadores luminosos en la carretera es de 40 meses; si una prueba previa
demostró que dichos indicadores duran 38 meses, con una desviación
estándar de 1 mes; determine:
a) Como deben proponerse las hipótesis nula y alternativa.
b) Con la información estadística indicada y un nivel de significancia de
alfa = 0.05 ¿la empresa estará diciendo la verdad?
Elaboró: MC. Marcel Ruiz Martínez
4