Prueba de Hipótesis y Chi Cuadrada
Anuncio

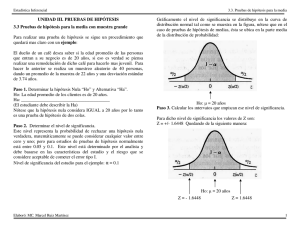
Ing. Rubén Darío Estrella, MBA Cavaliere dell’ordine al Merito della Repubblica Italiana (2003) Ingeniero de Sistemas (UNIBE 1993), Administrador (PUCMM 2000), Matemático (PUCMM 2007), Teólogo (UNEV 2002) y Maestro (Salomé Uneña 1985) [email protected] / [email protected] www.atalayadecristo.org Las hipótesis indican lo que estamos buscando o tratando de probar y pueden definirse como explicaciones tentativas del fenómeno investigado formuladas a manera de proposiciones. Las hipótesis no necesariamente son verdaderas, pueden o no serlo, pueden o no comprobarse con hechos. Son explicaciones tentativas, no los hechos en sí. Dentro de la investigación científica, las hipótesis son proposiciones tentativas acerca de las relaciones entre dos o más variables y se apoyan en conocimientos organizados y sistematizados. Sampieri H., Roberto. "Metodología de la Investigación". McGraw Hill: Segunda Edición. 1998 BEST SELLER INTERNACIONAL. Hipótesis nulas son, en cierto modo, el reverso de las hipótesis de investigación. También constituyen proposiciones acerca de la relación entre variables; que sirven solo para refutar o negar lo que afirma la hipótesis de investigación. Hipótesis alternativas, como su nombre lo indica, son posibilidades "alternas" ante las hipótesis de investigación y nula: Ofrece otra descripción o explicación distintas a las que proporcionan estos tipos de hipótesis. Si la hipótesis de investigación establece: "esta silla es roja", y podrían formularse una o más hipótesis alternativas: ""esta silla es azul", "esta silla es verde", "esta silla es amarilla", etcétera. Hipótesis estadísticas son las transformaciones de las hipótesis de investigación, nulas y alternativas en símbolos estadísticos. Se pueden formular solo cuando los datos del estudio que se van a recolectar y analizar para probar o rechazar las hipótesis son cuantitativos (números, porcentajes, promedios). Es decir, el investigador traduce su hipótesis de investigación y su hipótesis nula (y cuando se formulan hipótesis alternativas, también estas) en términos estadísticos. En estadística, una hipótesis es una afirmación o declaración que se hace acerca de una propiedad de una población. Componentes de una Prueba de Hipótesis. Hipótesis nula (denotada por Ho) es una declaración acerca del valor de un parámetro de población (como la media) y debe contener la condición de igualdad escrita con el símbolo =, o . (Al efectuar realmente la prueba, operaremos bajo el supuesto de que el parámetro es igual a algún valor especifico.) En el caso de la media, la hipótesis nula se expresara en una de estas tres posibles formas: Ho: = algún valor Ho: algún valor Ho: algún valor Por ejemplo, la hipótesis nula que corresponde a la creencia común de que la temperatura corporal media es 98.6ºF se expresa como Ho:=98.6. Probamos la hipótesis nula directamente en el sentido de que suponemos que es verdad y llegamos a una conclusión que puede ser rechazar Ho o bien en no rechazar Ho. Nunca se puede aceptar la hipótesis nula como verdadera. El no rechazo de la hipótesis nula solamente significa que la evidencia muestral no es lo suficientemente fuerte como para llegar a su rechazo. Antes que se rechace la hipótesis nula, la media muestral debe diferir significativamente de la media poblacional planteada como hipótesis. Es decir, que la evidencia debe ser muy convincente y concluyente. Una conclusión con base en un rechazo de la hipótesis nula es más significativa que una que termine en una decisión de no rechazo. Diferencia estadísticamente insignificante En la diferencia entre el valor de la media poblacional bajo la hipótesis y el valor de la media muestral que es lo suficientemente pequeña como para atribuirla a un error de muestreo. Hipótesis Alternativa (denotada por Ha) es la declaración que debe ser verdad si la hipótesis nula es falsa. En el caso de la media, la hipótesis alternativa se expresara en una de tres posibles formas: Ha: algún valor Ha: > algún valor Ha: < algún valor Obsérvese que Ha es lo contrario de Ho. Por ejemplo, si Ho se da como =98.6, se sigue que la hipótesis alternativa esta dada por Ha: 98.6. Errores Tipo I y Tipo II. Al probar una hipótesis nula, llegamos a una conclusión de rechazarla o no rechazarla. Tales conclusiones a veces son correctas y a veces equivocadas. Hay dos tipos de errores que podemos cometer. Error Tipo I. El error de rechazar la hipótesis nula, dado que es verdadera. La probabilidad de cometer un error tipo I es igual al nivel de significancia, o valor en el que se prueba la hipótesis. Error Tipo II. Es no rechazar una hipótesis nula que es falsa. Usamos el símbolo para representar la probabilidad de error tipo II. Como controlar los errores tipo I y tipo II. practicas que podrían ser pertinentes: Consideraciones 1. Para cualquier fija, un aumento en el tamaño de muestra n hace que disminuya. Es decir, una muestra más grande reduce la posibilidad de cometer el error de no rechazar la hipótesis nula, dado que en realidad es falsa. 2. Para cualquier tamaño de muestra fijo n, una disminución de causara un incremento en . Por otra parte, un incremento en causara una disminución en . 3. Si queremos reducir tanto como , deberemos aumentar el tamaño de muestra. Estadística de Prueba. Una estadística de muestra o un valor basado en los datos de una muestra. Se utiliza una estadística de prueba para tomar la decisión de rechazar o no la hipótesis nula. Z = (X' - )/(/n) Z = (X' - )/(s/n) Región critica. El conjunto de todos los valores de la estadística de prueba que nos harían rechazar la hipótesis nula. Valor critico. El valor o valores que separan la región critica de los valores de la estadística de prueba que no nos harían rechazar la hipótesis nula. Los valores críticos dependen de la naturaleza de la hipótesis nula, la distribución de muestreo pertinente y el nivel de significancia . Las colas de una distribución son las regiones extremas delimitadas por valores críticos. Rechazamos la hipótesis nula Ho si nuestra estadística de prueba esta en la región critica o área de rechazo porque eso indica una discrepancia significativa entre la hipótesis nula y los datos de la muestra. Algunas pruebas son de cola izquierda, con la región critica situada en la región de extrema izquierda de la curva; otras podrían ser de cola derecha, con la región critica en la región de la extrema derecha bajo la curva. En las pruebas de dos colas, el nivel de significancia se divide equitativamente entre las dos colas que constituyen la región critica o área de rechazo. En las pruebas de cola derecha o izquierda, el área de la región critica es . Si examinamos la hipótesis nula Ho, deberemos poder deducir si una prueba es de cola derecha, de cola izquierda o de dos colas. La cola corresponderá a la región critica que contenga los valores que podrían contradecir significativamente la hipótesis nula. Vale la pena destacar que tanto en la prueba de cola a la izquierda como a la derecha el signo igual se coloca en la hipótesis nula. Esto es porque la hipótesis nula se esta probando a un valor especifico (como 5%) y el signo igual da a la hipótesis nula un valor especifico para probarla. Una prueba de cola a la izquierda tiene una zona de rechazo solo en la cola izquierda y se da bajo la condición de: Ho: algún valor Ha: < algún valor Una prueba de cola a la derecha tiene una zona de rechazo solo en la cola derecha y se da bajo la condición de: Ho: algún valor Ha: > algún valor Prueba de dos colas para Hay cuatro pasos involucrados prueba: Paso 1: Plantear las hipótesis Ho y Ha. en una Paso 2: Con base en los resultados de la muestra, calcular el valor del estadístico de prueba Z, t, F, X². Paso 3: Determinar la regla de decisión con baseen los valores críticos de Z, t, F, X². Paso 4: Interpretación y conclusiones. Caso I. Como gerente de compras de una gran empresa de seguros usted debe decidir si actualizar o no los computadores de la oficina. A usted se le ha dicho que el costo promedio de los computadores es de US$2,100. Una muestra de 64 minoristas revela un precio promedio de US$2,251, con una desviación estándar de US$812. ¿A un nivel de significancia del 5% parece que su información es correcta? Datos: Ho: =US$2,100 n=64 minoristas X'=US$2,251 precio promedio (de los computadores) de la muestra s=US$812 =5%=0.05 (nivel de significancia) Paso 1: Plantear las hipótesis. El gerente de compra desea probar la hipótesis de que la media poblacional es =US$2,100 bajo un nivel de significancia =5%=0.05. Debido a que se plantea la hipótesis de que =US$2,100, la hipótesis nula y la alternativa son: Ho: = 2,100 Ha: 2,100 Paso 2: Con base en los resultados de la muestra, calcular el valor del estadístico de prueba Z. Para probar la hipótesis, se calcula el estadístico de prueba Z, y se compara con los valores críticos de Z. Z = (X' - H)/(/n) Z = (X' - H)/(s/n) en donde X' es la media muestral H es el valor de la media poblacional bajo hipótesis nula s/n es el error estándar de la distribución muestral Ho: = 2,100 n=64 minoristas X'=US$2,251 s=US$812 Z = (2,251 - 2,100)/(812/8) Z = (151)/(101.5) Z = 1.49 Paso 3: Determinar la regla de decisión con base en los valores críticos de Z. El nivel de significancia del 5% se divide en dos colas. El 95% restante se divide por 2 para hallar el área de 0.4750. En la tabla Z esta área de 0.4750 da los valores críticos de Z de 1.96. La Regla de Decisión es: "No se rechaza la hipótesis nula sí -1.96 Z 1.96. Se rechaza sí Z < -1.96 o Z > 1.96. Vale la pena destacar que las zonas de rechazo están en ambas colas. Si Z < -1.96 o Z > 1.96, se rechaza la hipótesis nula. Paso 4: Interpretación y conclusiones. El paso final en la prueba de hipótesis es donde cae el valor del estadístico para la muestra y determinar si la hipótesis nula debería rechazarse o no. El valor del estadístico para la muestra es X'=US$2,251 produce una Z=1.49 ==> 1.49<1.96 y cae dentro de la zona de no rechazo. Interpretación: La diferencia entre el valor de la media poblacional bajo la hipótesis nula de = 2,100 y el valor de la media muestral de X'=US$2,251 es estadísticamente insignificante. Podría resultar simplemente del error de muestreo. De hecho sí =2,100; el 95% de todas las muestras de tamaño n=64 producirán valores de Z entre 1.96. Caso II. Un contrato de manejo laboral exige una producción diaria de 50 unidades. Una muestra de 150 días revela una media de 47.3, con una desviación estándar de 5.7 unidades. Fije =5% y determine si se cumple con la disposición del contrato. Caso III. Un gerente de una empresa considera que los empleados gastan un promedio de 50 minutos para llegar al trabajo. Se toma una muestra de 70 empleados que se toman en promedio 47.2 minutos con una desviación estándar de 18.9 minutos. Fije en 1% y pruebe la hipótesis. TAREA: Ejercicios 1 al 16 Págs. 204-205. Para entregar en la próxima clase. Caso I. Baskin-Robbins, la franquicia de helados, afirma que el numero de tiendas que se abre se ha incrementado por encima del promedio semanal de 10.4 experimentado en tiempo de escasez (The Wall Street Journal, febrero de 1997). ¿Existe alguna evidencia para sustentar esta afirmación si 50 semanas muestran una media de 12.5 y una desviación estándar de 0.66 tiendas? La gerencia esta dispuesta a aceptar una probabilidad del 4% de rechazo de la hipótesis nula si esta es cierta. Datos: N =50 semanas X‘ =12.5 tiendas de la muestra S =0.66 tiendas =4%=0.04 (nivel de significancia) Caso I. Baskin-Robbins, la franquicia de helados, afirma que el numero de tiendas que se abre se ha incrementado por encima del promedio semanal de 10.4 experimentado en tiempo de escasez (The Wall Street Journal, febrero de 1997). ¿Existe alguna evidencia para sustentar esta afirmación si 50 semanas muestran una media de 12.5 y una desviación estándar de 0.66 tiendas? La gerencia esta dispuesta a aceptar una probabilidad del 4% de rechazo de la hipótesis nula si esta es cierta. Paso 1: Plantear las hipótesis. La afirmación de que el incremento es por encima del promedio semanal de 10.4 sirve como hipótesis alternativa debido a que >10.4 no contiene el signo igual. Una prueba de cola a la derecha tiene una zona de rechazo solo en la cola derecha y se da bajo la condición de: Ho: algún valor Ha: > algún valor Ha: > 10.4 tiendas semanal Ho: 10.4 tiendas semanal Caso I. Baskin-Robbins, la franquicia de helados, afirma que el numero de tiendas que se abre se ha incrementado por encima del promedio semanal de 10.4 experimentado en tiempo de escasez (The Wall Street Journal, febrero de 1997). ¿Existe alguna evidencia para sustentar esta afirmación si 50 semanas muestran una media de 12.5 y una desviación estándar de 0.66 tiendas? La gerencia esta dispuesta a aceptar una probabilidad del 4% de rechazo de la hipótesis nula si esta es cierta. Paso 2: Con base en los resultados de la muestra, calcular el valor del estadístico de prueba Z. Para probar la hipótesis, se calcula el estadístico de prueba Z, y se compara con los valores críticos de Z. Z = (X' - H)/(/n) Z = (X' - H)/(s/n) en donde X' es la media muestral H es el valor de la media poblacional bajo hipótesis nula /n es el error estándar de la distribución muestral = (12.5 - 10.4)/(0.66/50) = 2.1/0.093 = 22.5 Caso I. Baskin-Robbins, la franquicia de helados, afirma que el numero de tiendas que se abre se ha incrementado por encima del promedio semanal de 10.4 experimentado en tiempo de escasez (The Wall Street Journal, febrero de 1997). ¿Existe alguna evidencia para sustentar esta afirmación si 50 semanas muestran una media de 12.5 y una desviación estándar de 0.66 tiendas? La gerencia esta dispuesta a aceptar una probabilidad del 4% de rechazo de la hipótesis nula si esta es cierta. Paso 3: Determinar la regla de decisión con base en los valores críticos de Z. El nivel de significancia del 4%. El 50% se resta de 4% para hallar el área de 0.46. En la tabla Z esta área de 0.46 da el valor critico de Z de 1.75. La Regla de Decisión es: "No se rechaza la hipótesis nula sí Z rechaza sí Z>1.75”. 1.75. Se Caso I. Baskin-Robbins, la franquicia de helados, afirma que el numero de tiendas que se abre se ha incrementado por encima del promedio semanal de 10.4 experimentado en tiempo de escasez (The Wall Street Journal, febrero de 1997). ¿Existe alguna evidencia para sustentar esta afirmación si 50 semanas muestran una media de 12.5 y una desviación estándar de 0.66 tiendas? La gerencia esta dispuesta a aceptar una probabilidad del 4% de rechazo de la hipótesis nula si esta es cierta. Paso 4: Interpretación y conclusiones. El paso final en la prueba de hipótesis es donde cae el valor del estadístico para la muestra y determinar si la hipótesis nula debería rechazarse o no. El valor del estadístico para la muestra produce una Z=22.5 ==> 22.5>1.75 y cae dentro de la zona de rechazo o región critica. Interpretación: La hipótesis nula se rechaza ya que en tiempo de escasez se abren mas de 10.4 tiendas semanal Caso II. Según Wall Street Journal (mayo 12 de 1997) muchas compañías de ropa deportiva están tratando de comercializar sus productos entre los mas jóvenes. El articulo sugirió que la edad promedio de los consumidores había caído por debajo de la media de 34.4 años que caracterizo los comienzo de la década. Si una muestra de 1000 clientes reporta una media de 33.2 años y una desviación de 9.4, ¿qué se concluye a un nivel de significancia de 4%? Caso III Un distribuidor de bebidas plantea la hipótesis de que las ventas por mes promedian US$12,000. Diez meses seleccionados como muestra reportan una media de US$11,277 y una desviación estándar de US$3,772. Si se utiliza un valor del 5%. ¿Que puede concluir acerca de la impresión que tienen el distribuidor sobre las condiciones del negocio? Ejercicios 33 al 40 Págs. 215-216. El Método de valor P para probar hipótesis. Dado una hipótesis nula y datos de muestra, el valor p refleja la verosimilitud de obtener los valores de muestra en cuestión suponiendo que la hipótesis nula realmente es verdad. Valor P (o valor de probabilidad) es la probabilidad de obtener un valor de la estadística de prueba que será al menos tan extremo como se obtiene a partir de los datos de muestra, suponiendo que la hipótesis es verdad. Valor P es el nivel más bajo de significancia (valor mínimo) al cual se puede rechazar la hipótesis nula. Es el área en la cola que está más allá del valor del estadístico para la muestra. El Método de valor P para probar hipótesis. Algunos criterios de decisión basados exclusivamente en el valor P: - Rechazar la hipótesis nula si el valor P es menor que el nivel de significancia, o igual a él. - No rechazar la hipótesis nula si el valor P es mayor que el nivel de significancia. Caso I. A comienzo de los años 90 Sony Corporation introdujo su Play Station de 32 bits en el mercado de los juegos de video. La gerencia esperaba que el nuevo producto incrementara las ventas mensuales en Estados Unidos por encima de los US$283,000,000 que Sony había experimentado en la década anterior. Una muestra de 40 meses reporto una media de US$297,000,000. Se asume una desviación estándar de US$97,000,000. Pruebe la hipótesis nula a un nivel de significancia del 1%. Calcule e interprete el valor p. Datos: n=40 meses X'=US$297,000,000 ventas de la muestra s=US$97,000,000 α=1%=0.01 (nivel de significancia) Caso I. A comienzo de los años 90 Sony Corporation introdujo su Play Station de 32 bits en el mercado de los juegos de video. La gerencia esperaba que el nuevo producto incrementara las ventas mensuales en Estados Unidos por encima de los US$283,000,000 que Sony había experimentado en la década anterior. Una muestra de 40 meses reporto una media de US$297,000,000. Se asume una desviación estándar de US$97,000,000. Pruebe la hipótesis nula a un nivel de significancia del 1%. Calcule e interprete el valor p. Paso 1: Plantear las hipótesis. La afirmación de que el nuevo producto incrementara las ventas por encima de US$283,000,000 sirve como hipótesis alternativa debido a que µ > US$283,000,000 no contiene el signo igual. Una prueba de cola a la derecha tiene una zona de rechazo solo en la cola derecha y se da bajo la condición de: Ho: µ ≤ algún valor Ha: µ > algún valor Ha: µ > US$283,000,000 (ventas mensuales) Ho: µ ≤ US$283,000,000 (ventas mensuales) Caso I. A comienzo de los años 90 Sony Corporation introdujo su Play Station de 32 bits en el mercado de los juegos de video. La gerencia esperaba que el nuevo producto incrementara las ventas mensuales en Estados Unidos por encima de los US$283,000,000 que Sony había experimentado en la década anterior. Una muestra de 40 meses reporto una media de US$297,000,000. Se asume una desviación estándar de US$97,000,000. Pruebe la hipótesis nula a un nivel de significancia del 1%. Calcule e interprete el valor p. Paso 2: Con base en los resultados de la muestra, calcular el valor del estadístico de prueba Z. Para probar la hipótesis, se calcula el estadístico de prueba Z, y se compara con los valores críticos de Z. Z = (X' - µ H)/(σ/√n) Z = (X' - µ H)/(s/√n) Ho: US$283,000,000 (ventas mensuales) n=40 meses X'=US$297,000,000 ventas de la muestra s=US$97,000,000 α =1%=0.01 (nivel de significancia) Z = (297,000,000 283,000,000)/(97,000,000/40) Z = 14,000,000/15,337,047.42 = 0.91 Caso I. A comienzo de los años 90 Sony Corporation introdujo su Play Station de 32 bits en el mercado de los juegos de video. La gerencia esperaba que el nuevo producto incrementara las ventas mensuales en Estados Unidos por encima de los US$283,000,000 que Sony había experimentado en la década anterior. Una muestra de 40 meses reporto una media de US$297,000,000. Se asume una desviación estándar de US$97,000,000. Pruebe la hipótesis nula a un nivel de significancia del 1%. Calcule e interprete el valor p. El valor Z para el nivel de insignificancia de 1% se obtiene en la tabla después de restar 0.5-0.01= 0.49, el cual corresponde a 2.33 Paso 3: Determinar la regla de decisión con base en los valores críticos de Z. En la tabla Z el valor Z de 0.91 tiene el área de 0.3186. Por lo tanto el: valor P = 0.5 - 0.3186 = 0.1814 La Regla de Decisión es: - Rechazar la hipótesis nula si el valor P es menor que el nivel de significancia, o igual a él. - No rechazar la hipótesis nula si el valor P es mayor que el nivel de significancia. Caso I. A comienzo de los años 90 Sony Corporation introdujo su Play Station de 32 bits en el mercado de los juegos de video. La gerencia esperaba que el nuevo producto incrementara las ventas mensuales en Estados Unidos por encima de los US$283,000,000 que Sony había experimentado en la década anterior. Una muestra de 40 meses reporto una media de US$297,000,000. Se asume una desviación estándar de US$97,000,000. Pruebe la hipótesis nula a un nivel de significancia del 1%. Calcule e interprete el valor p. Paso 4: Interpretación y conclusiones. El paso final en la prueba de hipótesis es donde cae el valor del estadístico para la muestra y determinar si la hipótesis nula debería rechazarse o no. Como el valor de significancia es menor que 0.1814 para la muestra de Z=0.91 cae en la zona de no rechazo. Interpretación: La hipótesis nula no se rechaza. Caso II. En el verano de 1997, el Congreso de USA aprobó un presupuesto federal que contenía varias partidas para reducciones de impuestos. Los analistas afirmaron que ahorraría al contribuyente promedio US$800.00 dólares. Una muestra de 500 contribuyentes demostró una reducción promedio en los impuestos de US$785.10 con una desviación estándar de US$277.70. Pruebe la hipótesis a un nivel de significancia del 5%. Calcule e Interprete el valor p. Datos: n= 500 contribuyentes X'=US$785.10 s=US$277.70 α =5%=0.05 (nivel de significancia) Paso 1: Plantear las hipótesis. Ho: µ = US$800.00 Ha: µ US$800.00 Caso II. En el verano de 1997, el Congreso de USA aprobó un presupuesto federal que contenía varias partidas para reducciones de impuestos. Los analistas afirmaron que ahorraría al contribuyente promedio US$800.00 dólares. Una muestra de 500 contribuyentes demostró una reducción promedio en los impuestos de US$785.10 con una desviación estándar de US$277.70. Pruebe la hipótesis a un nivel de significancia del 5%. Calcule e Interprete el valor p. Paso 2: Con base en los resultados de la muestra, calcular el valor del estadístico de prueba Z. Z = (X' - µ H)/(σ/√n) Z = (X' - µ H)/(s/√n) = (785.10 – 800.00)/(277.70/500) = -14.9/12.42 = - 1.20 Caso II. En el verano de 1997, el Congreso de USA aprobó un presupuesto federal que contenía varias partidas para reducciones de impuestos. Los analistas afirmaron que ahorraría al contribuyente promedio US$800.00 dólares. Una muestra de 500 contribuyentes demostró una reducción promedio en los impuestos de US$785.10 con una desviación estándar de US$277.70. Pruebe la hipótesis a un nivel de significancia del 5%. Calcule e Interprete el valor p. El valor Z para el nivel de insignificancia de 5% se divide entre dos. Se obtiene en la tabla el valor de Z = 1.96. Paso 3: Determinar la regla de decisión con base en los valores críticos de Z. En la tabla Z, el valor Z de 1.20 tiene el área de 0.3849. Por lo tanto el: 0.5 - 0.3849 = 0.1151 valor P = 2 * 0.1151 = 0.2302 La Regla de Decisión es: - Rechazar la hipótesis nula si el valor P es menor que el nivel de significancia, o igual a él. - No rechazar la hipótesis nula si el valor P es mayor que el nivel de significancia. Caso II. En el verano de 1997, el Congreso de USA aprobó un presupuesto federal que contenía varias partidas para reducciones de impuestos. Los analistas afirmaron que ahorraría al contribuyente promedio US$800.00 dólares. Una muestra de 500 contribuyentes demostró una reducción promedio en los impuestos de US$785.10 con una desviación estándar de US$277.70. Pruebe la hipótesis a un nivel de significancia del 5%. Calcule e Interprete el valor p. Paso 4: Interpretación y conclusiones. El paso final en la prueba de hipótesis es donde cae el valor del estadístico para la muestra y determinar si la hipótesis nula debería rechazarse o no. Como el valor de significancia es menor que 0.2302 para la muestra de Z = -1.20 cae en la zona de no rechazo. Interpretación: La hipótesis nula no se rechaza. En secciones anteriores determinamos (1) el estimado puntual, (2) intervalo de confianza y (3) determinamos el tamaño de la muestra para medias y proporciones, en esta sección los aplicaremos a la varianza de población ² o desviación estándar de población . Muchas situaciones reales, como el control de calidad en un proceso de fabricación, requiere estimar valores de varianzas o desviaciones estándar de población. Además de fabricar productos cuyas mediciones producen una media deseada, el fabricante debe elaborar productos con una calidad uniforme que no abarquen toda la gama desde extremadamente buenos hasta extremadamente deficientes. Dado que tal uniformidad a menudo se puede medir por la varianza o la desviación estándar, estas se convierten en estadísticas vitales para mantener la calidad de los productos. En una población distribuida normalmente con varianza ², seleccionamos aleatoriamente muestras independientes de tamaño n y calculamos la varianza de muestras s² para cada muestra. La estadística de muestra ²=(n-1)s²/² tiene una distribución llamada distribución Chi cuadrada. ²=(n-1)s²/² n = tamaño de muestra s²= varianza de muestra ²= varianza de población La distribución Chi cuadrada esta determinada por el numero de grados de libertad, por el momento usaremos n-1 grados de libertad. Propiedades de la Distribución de la estadística Chi cuadrada. 1.- La Distribución Chi cuadrada no es simétrica, a diferencia de las distribuciones normal y t Student (A medida que aumenta el número de grados de libertad, la distribución se vuelve más simétrica). 2.- Los valores de Chi cuadrada pueden ser cero o positivos, pero no pueden ser negativos. 3.- La distribución Chi cuadrada es diferente para cada número de grados de libertad, que es gl=n-1. A medida que aumenta el numero de grados de libertad, la distribución Chi cuadrada se acerca a una distribución normal. Caso I. Usando la tabla H Distribución Chi-cuadrado. Encuentre los valores críticos de ² que determinan regiones críticas que contienen un área de 0.025 en cada cola. Suponga que el tamaño de muestra pertinente es de 10, de modo que el número de grados de libertad es 10-1=9 Solución: El valor crítico de la derecha (²=19.023) se obtiene directamente localizando 9 en la columna de grados de libertad de la izquierda y 0.025 en la fila superior. El valor crítico de ²=2.700 de la izquierda también corresponde a 9 en la columna de grados de libertad, pero es preciso localizar 0.975 (que se obtiene de restar 0.025 a 1) en la fila superior porque los valores de esa fila siempre son áreas a la derecha del valor critico. Al obtener valores críticos de Chi cuadrada de la Tabla H Distribución Chi-cuadrado, obsérvese que los números de grados de libertad son enteros consecutivos del 1 al 30, seguidos de 40, 50, 60, 70, 80, 90 y 100. Si no se encuentra en la tabla un número de grados de libertad (digamos 52), por lo regular puede usarse el valor crítico más cercano. Por ejemplo, si el número de grados de libertad es 52, remítase a la tabla y use 50 grados de libertad. (Si el número de grados de libertad esta exactamente a la mitad entre dos valores de la tabla, como 55, simplemente calcule la media de los dos valores de ².) Para números de grados de libertad mayores que 100, use la ecuación siguiente: ²=1/2 [Z+(2k-1)]² donde k es el numero de grados de libertad. Caso II. Encuentre los valores críticos ²L y ²R que corresponden al grado de confianza y tamaño de muestra dados. 1. 95%; n=26 3. 90%; n=60 2. 99%; n=17 4. 95%; n=50 Estimadores de ². Dado que las varianzas de muestras s² (que se obtienen con la formula s²=[(x-x')²]/(n-1)) tienden a centrarse alrededor del valor de la varianza de la población ², decimos que s² es un estimador no predispuesto de ². Es decir, las varianzas de muestras s² no tienden a sobreestimar sistemáticamente ²; en vez de ello, tienden a centrarse en el valor de ² mismo. Además, los valores s² tienden a producir errores más pequeños al estar mas cerca de ² que otras medidas de variación. Por estas razones, el valor s² es el mejor valor individual (o estimado puntual) de las diversas estadísticas que podríamos usar para estimar ². La varianza de muestra s² es el mejor estimado puntual de la variación de la población ². Dado que s² es el mejor estimado puntual de ², sería natural esperar que s sea el mejor estimado puntual de , pero no sucede así, porque s es un estimador predispuesto de . Por otra parte, si el tamaño de muestra es grande, la predisposición es tan pequeña que podemos usar s como un estimado razonablemente bueno de . Aunque s² es el mejor estimado puntual de ², no tenemos una indicación de lo bueno que es realmente. Para compensar esta deficiencia, deducimos un estimado de intervalo (o intervalo de confianza) que es más revelador. Intervalo de confianza (o estimado de intervalo) para la varianza de población ². Despeje: El intervalo de confianza es: ²=(n-1)s²/² ²=(n-1)s²/² (n-1)s²/²R < ² < (n-1)s²/²L El intervalo de confianza para la desviación estándar se obtiene calculando la raíz cuadrada de cada componente anterior: [(n-1)s²/²R] < < [(n-1)s²/²L] Con un área total de dividida equitativamente entre las dos colas de una distribución Chi cuadrada, ²L denota el valor critico de cola izquierda y ²R denota el valor critico de cola derecha. Los limites de intervalos de confianza para ² y se deben redondear aplicando la regla de redondeo siguiente: 1. Si usa el conjunto de datos original para construir un intervalo de confianza, redondee los limites del intervalo de confianza a una posición decimal más que las empleadas en el conjunto de datos original. 2. Si desconoce el conjunto de datos original y sólo usa las estadísticas resumidas (n,s), redondee los limites del intervalo de confianza al mismo número de posiciones decimales que se usan para la desviación estándar o varianza de muestra. Caso I. La Panificadora Pepin produce bizcochos que se empacan en cajas cuyos rótulos dicen contienen 12 bizcochos con un total de 42 onzas. Si la variación entre los bizcochos es demasiado grande, algunas cajas pesaran menos de lo debido (engañando a los clientes) y otras pesaran más (reduciendo las utilidades). El supervisor de control de calidad determino que puede evitar problemas si los bizcochos tienen una media de 3.50 onzas y una desviación estándar de 0.06 onzas o menos. Se seleccionan aleatoriamente doce bizcochos de la línea de producción y se pesan, con los resultados que se dan aquí (en onzas). Construya un intervalo de confianza del 95% para ² y un intervalo de confianza del 95% para , y luego determine si el supervisor de control de calidad está en problemas. 3.43 3.37 3.58 3.50 3.68 3.61 3.42 3.52 3.66 3.50 3.36 3.42 s²=[(x-x')²]/(n-1)) X X-X' 3.43 -0.074 3.37 -0.134 3.58 0.076 3.5 -0.004 3.68 0.176 3.61 0.106 3.42 -0.084 3.52 0.016 3.66 0.156 3.5 -0.004 3.36 -0.144 3.42 -0.084 42.05 MEDIA VARIANZA 3.504 DESVIACION (X-X')^2 0.005 0.018 0.006 0.000 0.031 0.011 0.007 0.000 0.024 0.000 0.021 0.007 0.131 0.012 0.109 Descriptive statistics X count 12 mean 3.5042 sample variance 0.0119 sample standard deviation 0.1091 f(Chisq) 0 1 Chisq 2 3 4 5 6 7 8 9 10 11 12 13 14 3.82 Chi-square distribution df = 11 P(lower) P(upper) Chi-square .9750 .0250 21.92 .0250 .9750 3.82 15 16 17 18 19 20 21 22 21.92 23 24 25 Solución: Con base en los datos de muestra, la media de X'=3.504 parece excelente porque esta muy cerca del valor deseado. Los puntajes dados tienen una desviación estándar de s=0.109, que podría parecer mayor que el valor deseado de 0.06 o menos. Procedamos a obtener el intervalo de confianza para ². Con una muestra de 12 puntajes tenemos 11 grados de libertad. Con un grado de confianza del 95%, dividimos =0.05 equitativamente entre las dos colas de la distribución ² y nos remitimos a los valores de 0.975 y 0.025 en la fila superior. Los valores críticos de ² son ²L=3.816 y ²R=21.920. Utilizando estos valores críticos junto con la desviación estándar de muestra s=0.109 y el tamaño de muestra de 12 construimos el intervalo de confianza del 95% evaluando lo siguiente: (n-1)s²/²R < ² < (n-1)s²/²L (12-1)(0.109)²/21.920 < ² < (12-1)(0.109)²/(3.816) 0.006 < ² < 0.034 Si sacamos la raíz cuadrada de cada parte (antes de redondear) obtenemos: 0.077 < < 0.185 Con base en el intervalo de confianza del 95% para , parece que la desviación estándar es mayor que el valor deseado de 0.06 o menos, así que el supervisor de control de calidad está en problemas y deberá tomar medidas correctivas para hacer que el peso de los bizcochos sea más uniforme. El intervalo de confianza de 0.077 < < 0.185 también puede expresarse como (0.077,0.185), pero el formato de =sE no puede usarse porque el intervalo de confianza no tiene a s en su centro. Caso II. Un recipiente anticongelante para automóvil supuestamente contiene 3,785 ml del liquido. Consciente de que las fluctuaciones son inevitables, la gerente de control de calidad quiere estar muy segura de que la desviación estándar sea de menos de 30 ml; De lo contrario, algunos recipientes se desbordaran, mientras que otros no tendrán suficiente anticongelantes. Ella selecciona aleatoriamente una muestra, con los resultados que se dan aquí. Utilice estos resultados para construir el intervalo de confianza del 99% para el verdadero valor de . ¿Sugiere este intervalo de confianza que las fluctuaciones están en un nivel aceptable? 3,761 3,861 3,769 3,772 3,675 3,861 3,888 3,819 3,788 3,800 3,720 3,748 3,753 3,821 3,811 3,740 3,740 3,839 N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 MEDIA X X-X' (X-X')^2 3,761.00 -26.00 676.00 3,861.00 74.00 5,476.00 3,769.00 -18.00 324.00 3,772.00 -15.00 225.00 3,675.00 -112.00 12,544.00 3,861.00 74.00 5,476.00 3,888.00 101.00 10,201.00 3,819.00 32.00 1,024.00 3,788.00 1.00 1.00 3,800.00 13.00 169.00 3,720.00 -67.00 4,489.00 3,748.00 -39.00 1,521.00 3,753.00 -34.00 1,156.00 3,821.00 34.00 1,156.00 3,811.00 24.00 576.00 3,740.00 -47.00 2,209.00 3,740.00 -47.00 2,209.00 3,839.00 52.00 2,704.00 3,787.00 VARIANZA 3,066.82 DESVIACION 55.38 Descriptive statistics X count 18 mean 3,787.0000 sample variance 3,066.8235 sample standard55.3789 deviation minimum 3675 maximum 3888 range 213 Con una muestra de 18 puntajes tenemos 17 grados de libertad. Con un grado de confianza del 99%, dividimos =0.01 equitativamente entre las dos colas de la distribución ² y nos remitimos a los valores de 0.995 y 0.005 en la fila superior. Los valores críticos de ² son ²L=5.697 y ²R=35.718. Utilizando estos valores críticos junto con la desviación estándar de muestra s=55.38 y el tamaño de muestra de 18 construimos el intervalo de confianza del 99% evaluando lo siguiente: (n-1)s²/²R < ² < (n-1)s²/²L (18-1)(55.38)²/35.718 < ² < (18-1)(55.38)²/(5.697) 1,459.66 < ² < 9,151.48 Si sacamos la raíz cuadrada de cada parte (antes de redondear) obtenemos: 38.21 < < 95.6 Con base en el intervalo de confianza del 99% para , parece que la desviación estándar es mayor que el valor deseado de 30 ml, y algunos recipientes se desbordaran, así que el supervisor de control de calidad está en problemas y deberá tomar medidas correctivas. Caso III. a) Los valores que se listan son tiempos de espera (en minutos) de clientes del BHD, donde los clientes se forman en una sola fila que alimenta tres ventanillas. Construya un intervalo de confianza del 95% para la desviación estándar de la población . 6.5 6.6. 6.7 6.8 7.1 7.3 7.4 7.7 7.7 7.7 b) Los valores que se listan son tiempos de espera (en minuto) de clientes del Banco Popular, donde los clientes pueden formarse en cualquiera de tres filas distintas que se han formado frente a tres ventanillas distintas. Construya un intervalo de confianza del 95% para y compare los resultados con el intervalo de confianza para los datos del Banco BHD. ¿Sugieren los intervalos de confianza alguna diferencia en la variación de los tiempos de espera de cada banco? ¿Cuál sistema parece mejor: el de fila única o el de múltiples filas? 4.2 5.4 5.8 6.2 6.7 7.7 7.7 8.5 9.3 10.0 Caso IV. Se espera que un proceso estandarizado produzca arandelas con una desviación muy pequeña en su espesor. Suponga que se tomaron 10 de estas arandelas y sus espesores, en pulgadas fueron: 0.123 0.124 0.126 0.120 0.130 0.133 0.125 0.128 0.124 0.126 ¿Cuál es un intervalo de confianza de 90 por ciento para la desviación estándar del espesor de una arandela producida mediante este proceso? Determinación del tamaño de muestra. Los procedimientos para encontrar el tamaño de muestra necesario para estimar σ² son muchos más complejos que los procedimientos que se dieron antes para las medias y proporciones. En lugar de aplicar procedimientos muy complicados, usaremos la tabla 6-2. Caso I. Con una confianza del 95%, queremos estimar σ dentro de un margen de error del 10%. ¿Qué tamaño deberá tener la muestra? Supongamos que la población está distribuida normalmente. Solución: En la tabla 6-2 vemos que una confianza del 95% y un error del 10% para corresponde a un tamaño de muestra de 191. Deberemos seleccionar aleatoriamente 191 valores de la población. Caso II. Determine el tamaño de muestra mínimo necesario para tener una confianza del 95% en que la desviación estándar de la muestra s estará a menos del 30% de σ. Caso III. Determine el tamaño de muestra mínimo necesario para tener una confianza del 99% en que la desviación estándar de la muestra s estará a menos del 20% de σ. Caso IV. Determine el tamaño de muestra mínimo necesario para tener una confianza del 99% en que la varianza de la muestra estará a menos del 30% de la varianza de la población. Caso V. Determine el tamaño de muestra mínimo necesario para tener una confianza del 95% en que la varianza de la muestra estará a menos del 40% de la varianza de la población.