Uso de las distribuciones binomial, multinomial y Poisson con R

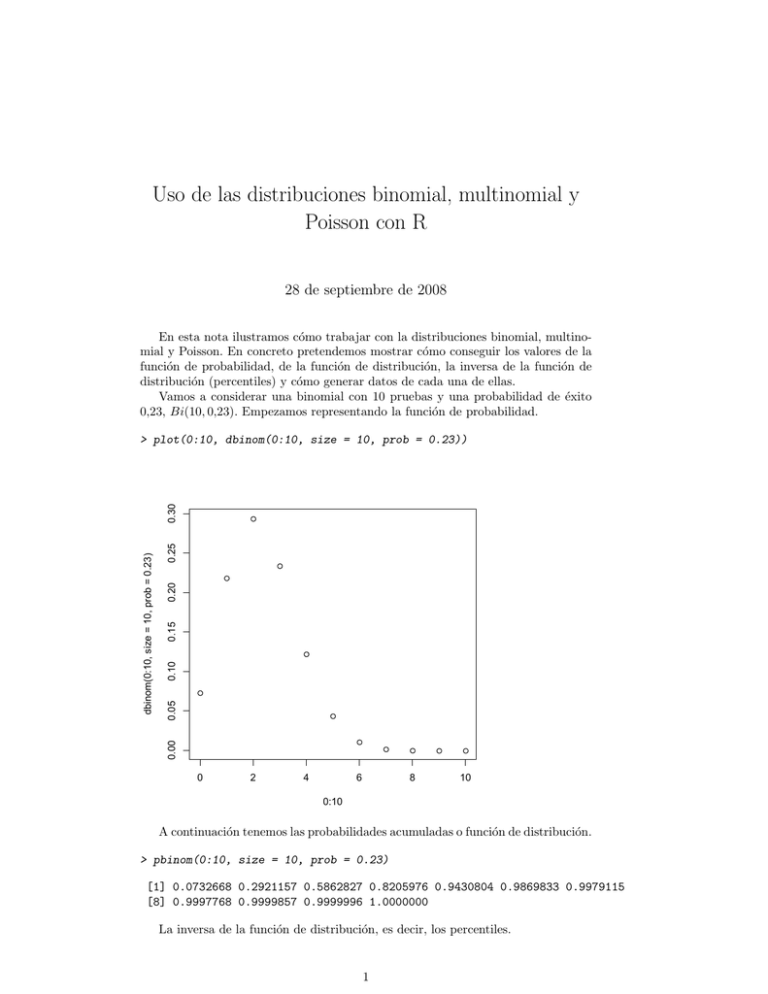
Uso de las distribuciones binomial, multinomial y
Poisson con R
28 de septiembre de 2008
En esta nota ilustramos cómo trabajar con la distribuciones binomial, multinomial y Poisson. En concreto pretendemos mostrar cómo conseguir los valores de la
función de probabilidad, de la función de distribución, la inversa de la función de
distribución (percentiles) y cómo generar datos de cada una de ellas.
Vamos a considerar una binomial con 10 pruebas y una probabilidad de éxito
0,23, Bi(10, 0,23). Empezamos representando la función de probabilidad.
0.25
●
●
0.15
0.20
●
0.10
●
0.05
●
●
●
0.00
dbinom(0:10, size = 10, prob = 0.23)
0.30
> plot(0:10, dbinom(0:10, size = 10, prob = 0.23))
●
0
2
4
6
●
8
●
●
10
0:10
A continuación tenemos las probabilidades acumuladas o función de distribución.
> pbinom(0:10, size = 10, prob = 0.23)
[1] 0.0732668 0.2921157 0.5862827 0.8205976 0.9430804 0.9869833 0.9979115
[8] 0.9997768 0.9999857 0.9999996 1.0000000
La inversa de la función de distribución, es decir, los percentiles.
1
> qbinom(0.3, size = 10, prob = 0.23)
[1] 2
Los valores binomiales los generamos del siguiente modo.
> rbinom(100, size = 10, prob = 0.23)
[1] 4 2 1 3 3 0 4 3 1 2 5 1 3 2 2 2 2 2 4 2 1 4 0 0 2 3 5 3 5 4 1 2 3 2 3 1 2
[38] 2 0 1 2 2 3 2 2 2 1 0 3 0 3 2 5 3 1 2 1 0 1 2 2 4 2 2 0 1 1 0 2 2 3 2 2 1
[75] 2 3 4 4 3 2 2 1 3 4 4 4 1 4 4 3 3 0 2 2 1 4 6 1 0 1
En lo anterior hemos visto que la función de probabilidad viene precedida de
la letra d, la función de distribución de la letra p, los percentiles de la letra q
y finalmente generamos con la función que empieza por r. Esto es ası́ en R para
cualquier distribución de probabilidad.
Siguiendo esta convención podemos generar para la multinomial
> rmultinom(10, size = 12, prob = c(0.1, 0.2, 0.8))
[1,]
[2,]
[3,]
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
0
1
4
2
0
1
1
1
0
0
3
2
1
2
3
3
3
3
4
2
9
9
7
8
9
8
8
8
8
10
O bien calcular la probabilidad conjunta del vector (3, 7, 2) o del vector (1, 2, 8).
> dmultinom(c(3, 7, 2), prob = c(0.1, 0.2, 0.8))
[1] 2.067297e-05
> dmultinom(c(1, 2, 8), prob = c(0.1, 0.2, 0.8))
[1] 0.1164302
Y acabamos mostrando las funciones de probabilidad, distribución, percentiles
y generación de la variable de Poisson.
> dpois(0:30, lambda = 12)
[1]
[6]
[11]
[16]
[21]
[26]
[31]
6.144212e-06
1.274064e-02
1.048373e-01
7.239112e-02
9.682032e-03
3.778781e-04
5.498491e-06
7.373055e-05
2.548128e-02
1.143679e-01
5.429334e-02
5.532590e-03
1.744053e-04
4.423833e-04
4.368219e-02
1.143679e-01
3.832471e-02
3.017776e-03
7.751345e-05
1.769533e-03
6.552328e-02
1.055704e-01
2.554981e-02
1.574492e-03
3.322005e-05
5.308599e-03
8.736438e-02
9.048890e-02
1.613672e-02
7.872460e-04
1.374623e-05
> ppois(10:20, lambda = 12)
[1] 0.3472294 0.4615973 0.5759652 0.6815356 0.7720245 0.8444157 0.8987090
[8] 0.9370337 0.9625835 0.9787202 0.9884023
> qpois(seq(0.1, 0.9, 0.1), lambda = 12)
[1]
8
9 10 11 12 13 14 15 17
> rpois(50, lambda = 12)
[1] 18 11 15 14 16 10 16
[26] 18 15 16 10 7 14 8
5 16 8 9 10 12 10 12 17 12 7 10 14 12 8 11 13 12
7 13 10 14 9 16 12 7 12 14 13 8 8 9 16 19 9 15
2