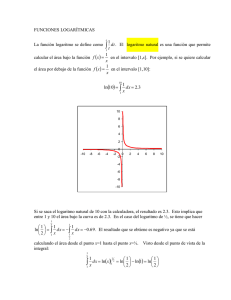
a ( )= log

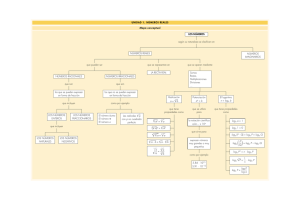
UNIDAD 9 Derivadas. Técnicas de derivación
4. Repaso teórico: propiedades de los logaritmos
Pág. 1 de 1
LOGARITMOS. PROPIEDADES
Si a > 0 y a ≠ 1, se llama logaritmo en base a de P, y se designa loga P, al exponente al que hay que elevar la
base a para obtener P.
loga P = x ï ax = P
Por ejemplo:
log2 8 = 3 porque 8 = 23,
log2
1
1
1
= –3 porque
= 3 = 2–3
8
8
2
log5 25 = 2 porque 25 = 52,
log5
1
1
1
= –2 porque
= 2 = 5–2
25
25
5
log10 10 000 = 4 porque 10 000 = 104
log10 0,0001 = – 4 porque 0,0001 = 10–4
Te hacemos observar que los números que son potencias exactas de la base tienen logaritmos enteros. Los demás, tienen logaritmos con parte decimal.
Por ejemplo:
8
…
log2
11
…
log2
3
16
log2
3,…
4
El log2 11 es un número decimal cuya parte entera es 3.
Propiedades de los logaritmos
1 Dos números distintos tienen logaritmos distintos. Es decir:
Si P ≠ Q, entonces loga P ≠ loga Q.
Además, si a > 1 y P < Q, loga P < loga Q.
2 El logaritmo de la base es 1: loga a = 1, porque a1 = a
3 El logaritmo de 1 es 0, cualquiera que sea la base: loga 1 = 0, porque a0 = 1
4 El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
loga (P · Q ) = loga P + loga Q
5 El logaritmo de un cociente es igual al logaritmo del numerador menos el del denominador:
loga
( )
P
= loga P – loga Q
Q
6 El logaritmo de una potencia es igual al exponente por el logaritmo de la base de la potencia:
loga P n = n log a P
7 El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice:
n
loga √P =
loga P
n
8 Cambio de base. El logaritmo en base a de un número se puede obtener a partir de logaritmos en otra base:
loga P =
logb P
logb a