Pendientes 1º Bº.Números 1y2

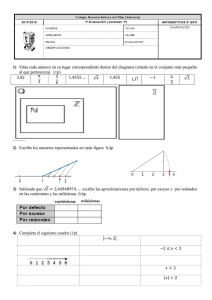
Números 1: Radicales. Intervalos.
1.
1º Bachillerato C yT
Realiza las operaciones indicadas:
1
a)
6
5
c) 5 2 + 3 8 –
3
16
6a  25a
2
4
3
d) 4 12 –
18
4
2á 3á 4
e)
3a 
b)
f)
g) (3 2  2 3)(3 3  2 2)
h)
3
48 –
2
2
8
3
27 +
3
75
5
a á4 2a ÊÊ
aá a á3 a á4 a Ê
2. Simplificar las siguientes expresiones, operando con las raices:
a)
2 3 4
b)
7
3 1
7
7
c)
2· 2· 8
3
d) 3
2 2
a
b
a
b
3. Racionaliza y simplifica las siguientes expresiones:
a)
5
b)
3 6
3–
2 2+
2
3
c)
2y
2–
d)
y
7
5
e)
2
7
1–
7
4. Realiza las siguientes operaciones:
(
a) 3 +
d)
2
2
2
 1

b) 
 3 Ê
 3

)
(3 8  50  72)á 2
3
24
e)
2
2

3 2
2 1

c) (
1
5
 10)á(
1
5
 10)
1
4
f)
2 2
1
1
2
1
2
5. Representa como intervalos los conjuntos de números que verifican:
a) x   2
b) x-2 7
c) x  3
d) 2x+4   10
e) x+1 > 7
f) x - 3  1
g) [-3, 8)  (-5, 2]
h) (- , 5)  (-2, 7)
k) 3x + 4  5
l) 5 > 3x 
i) (-, -2)  (-4, -3)
j) (3, 8]  (-5, +)
6. Comprueba las siguientes igualdades:
a)
42 3 
42 3 2
b)
2 1
2 1

2 1
2 1
2
Números 2: Logaritmos. Errores. Notación científica
1º Bachillerato CyT
1. ¿Cuáles de las siguientes igualdades son válidas?:
a) log 35 = (log 7)(log 5)
b) log 49 = 2 log 7
c) ln 75 = ln 70 + ln 5
d) log2 10 = log 2
2. Sabiendo que loga 2 = 0´4 y loga 3 = 0´6 calcula:
a) loga 6 b) loga 9
c) loga 64
d) loga 24
e) loga
3
f) b) loga (2/3)5
36
3. Calcula el valor de x en las siguientes expresiones:
a) loga x = 0
b) log7 x = 2
e) logx 10 = 1/4
f) log2
1
16
c) log6
=x
i) loga x = loga 9 - loga 4
3
36 = x
g) log8 x =
d) log2 64 = x
1
3
h) logx 10 = 0
j) loga x = 3( loga 5 + 4 loga 2 - loga 3)
4. Se han medido la longitud y la anchura de un muro con una cinta métrica de 50 metros, obteniéndose 40
m para la primera y 40 cm para la segunda. Al rebobinar la cinta, se dan cuenta de que faltaban los dos
primeros centímetros. Estudia el error absoluto y relativo cometido en ambas medidas.
5. Se quiere cercar un terreno en forma de triángulo rectángulo siendo los catetos de 1km y 2km
a) ¿Qué longitud de valla se necesita?
b) ¿Con qué aproximación has tomado
5
? Repite el cálculo con un decimal más.
c) ¿Cuántos metros de terreno quedarían sin cercar si tomamos
d) Y si tomamos
5
5
como 2'23 ?
como 2'24 ¿sobrará o faltará valla?¿cuántos metros?
6. a) Si quisiéramos cambiar el cristal roto de una ventana, con qué precisión darías las medidas al
cristalero? ¿Por qué?
b) Si quisiéramos dar la distancia de Zaragoza a Barcelona, ¿con qué precisión la tendríamos que dar?
7. ¿Dónde hemos cometido más error? diciendo que un lápiz de 0’14 m mide 0’15 m, o diciendo que una
pared de 2’73 m mide 2’76 m?¿Por qué?
12
8. La distancia de la Tierra a Sirius es 81' 78 x 10
km. Si disponemos de una nave espacial, capaz de
viajar a 1.000 km/s. ¿Cuánto tardaríamos en llegar?
-18
9. El ser vivo más pequeño es un virus que pesa del orden de 10
g y el más grande es la ballena azul, que
pesa, aproximadamente, 138 t. ¿Cuántos virus serían necesarios para conseguir el peso de una ballena?
10. La distancia media de Neptuno al Sol es, aproximadamente, 30 veces la de la Tierra al Sol (150 millones
de km). Expresa en notación científica la distancia máxima y la distancia mínima entre la Tierra y
Neptuno.
11. En 22'4 litros de cualquier gas hay 6'02 x 10
250 cc ?
23
moléculas. ¿Cuántas moléculas habrá en una botella de
12. Efectúa las siguientes operaciones, con tu calculadora:
3
a)
4
5.102.345 x 0'000456
-3
234'35
;
b)

-2
4

0'00038
2'5x105 x
4 
13'904 
