1) Sitúa cada número en su lugar correspondiente dentro del

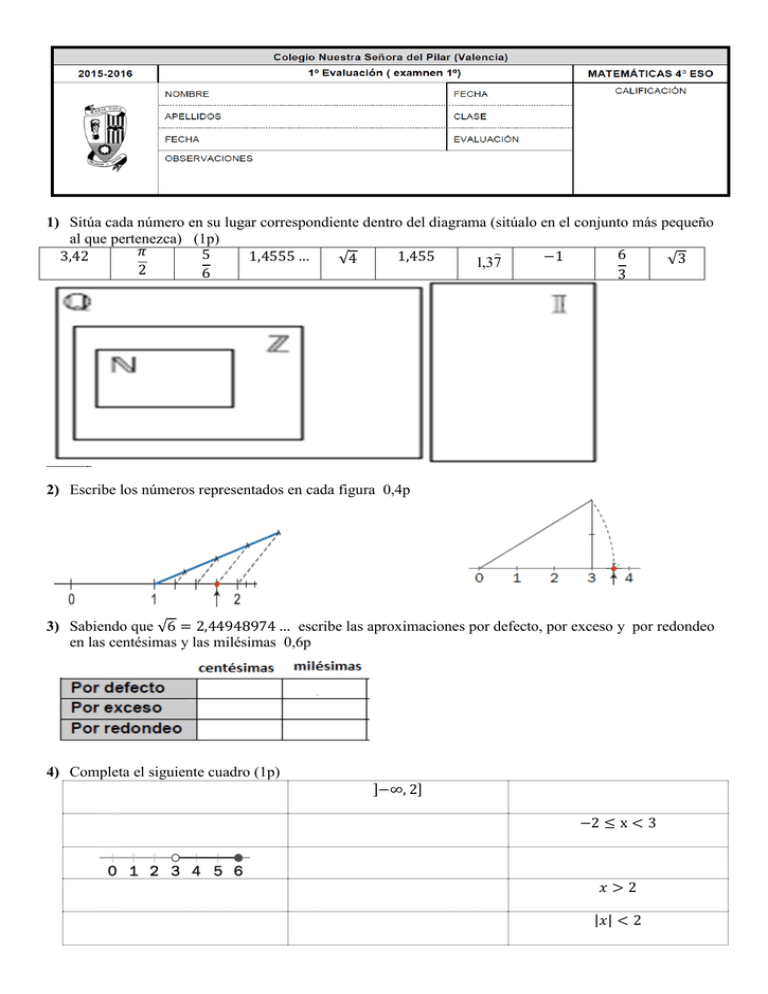
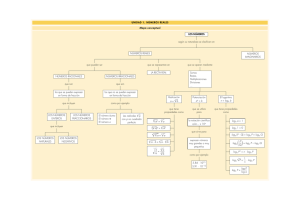
1) Sitúa cada número en su lugar correspondiente dentro del diagrama (sitúalo en el conjunto más pequeño
al que pertenezca) (1p)

𝜋
5
6
3,42
1,4555 …
1,455
−1
√4
√3
1,37
2
6
3
2) Escribe los números representados en cada figura 0,4p
3) Sabiendo que √6 = 2,44948974 … escribe las aproximaciones por defecto, por exceso y por redondeo
en las centésimas y las milésimas 0,6p
4) Completa el siguiente cuadro (1p)
]−∞, 2]
−2 ≤ x < 3
𝑥>2
|𝑥| < 2
5) Escribe los siguientes números en notación científica (0,6p)
5000 =
0,0057 =
0,35 ∙ 104 =
23 ∙ 10−5 =
6) Aplicando las propiedades de las potencias, simplifica las expresiones paso a paso y exprésalo como
una única potencia. (0,4p)
  5
25  5 
5 2  5 2
3
2 2
4

7) Racionaliza y simplifica al máximo (1,75p)
5
3
√25
=
√3 − √6
√3 + √6
=
8) Opera y simplifica 0,5p
3√20 − 2√80 − √45 =
9) Utilizando la definición del logaritmo, halla el valor de X ( indicando todos los pasos de forma
razonada) 1,5p
log x 16  4
log 2 x  2
3
log
2
1
x
4
10) Determinar si las siguientes igualdades son ciertas o falsas. Si son falsas escribir correctamente: 0,5p
a.
b.
c.
d.
e.
loga A
b
loga (A  B)  loga A  loga B
log2  100
loga A
A
loga   
 B  loga B
loga A  loga B  loga ( A  B)
loga b A 
11) Utilizando las propiedades de los logaritmos despeja la incógnita A de las siguientes expresiones
logarítmicas: ( paso a paso) (0,5 p)
log d  1  3 log x  log y
12) Utilizando las propiedades de los logaritmos, pasa a forma logarítmica la siguiente expresión algebraica.
(Paso a paso) (0, 5p)
𝐴=
𝑥2𝑦
𝑧𝑡 3
13) Sabiendo que
𝑙𝑜𝑔80 =
𝒍𝒐𝒈𝟖 ≅ 𝟎, 𝟗𝟎𝟑
calcula (aplicando las propiedades de los logaritmos, paso a paso) (0,75p)
3
𝑙𝑜𝑔64=
𝑙𝑜𝑔 √800 =
1.-Sitúa cada número en su lugar correspondiente dentro del diagrama (sitúalo en el conjunto más pequeño al que
pertenezca) (1p)
3,42̂
𝜋
2
5
6
1,455
1,4545 …
√4
1,37
−1
6
3
√3
2.- Escribe los números representados en cada figura 0,4p
3.- Sabiendo que √5 = 2,2360679 … escribe las aproximaciones por defecto, por exceso y por redondeo en las
centésimas y las milésimas 0,6p
4.- Completa el siguiente cuadro (1p)
]−1,2]
−2 < x ≤ 3
𝑥<2
|𝑥| < 1
5.- Escribe los siguientes números en notación científica (0,6p)
500 =
0,057 =
0,35 ∙ 105 =
23 ∙ 10−4 =
6.- Aplicando las propiedades de las potencias, simplifica las expresiones paso a paso y exprésalo como una única
potencia. (0,4p)
 
2
5 1  5 2  55

25  5
7.- Racionaliza y simplifica al máximo (1,75p)
3
3
√9
=
√3 + √6
√3 − √6
=
8.- Opera y simplifica 0,5p
√12 − 4√27 + 3√75 =
9.- Utilizando la definición del logaritmo, halla el valor de X ( indicando todos los pasos de forma razonada) 1,5p
log x 16  4
log 2 x  2
log
3
2
1
x
4
10.-Determinar si las siguientes igualdades son ciertas o falsas. Si son falsas escribir correctamente: 0,5p
a.
b.
c.
d.
e.
loga A
b
loga (A  B)  loga A  loga B
log2  100
loga A
A
loga   
 B  loga B
loga A  loga B  loga ( A  B)
loga b A 
11.-Utilizando las propiedades de los logaritmos despeja la incógnita A de las siguientes expresiones logarítmicas:
(paso a paso) (0,5 p)
log d  3 log x  log y  2
12.- Utilizando las propiedades de los logaritmos, pasa a forma logarítmica la siguiente expresión algebraica:
(paso a paso) (0, 5p)
𝐴=
𝑥 2 √𝑦
𝑧
13.- Sabiendo que
𝑙𝑜𝑔800 =
𝒍𝒐𝒈𝟖 ≅ 𝟎, 𝟗𝟎𝟑
calcula (aplicando las propiedades de los logaritmos, paso a paso) (0,75p)
𝑙𝑜𝑔640=
3
𝑙𝑜𝑔 √0,8 =