1. Función Compuesta Para que sea posible hallar GoF, se debe

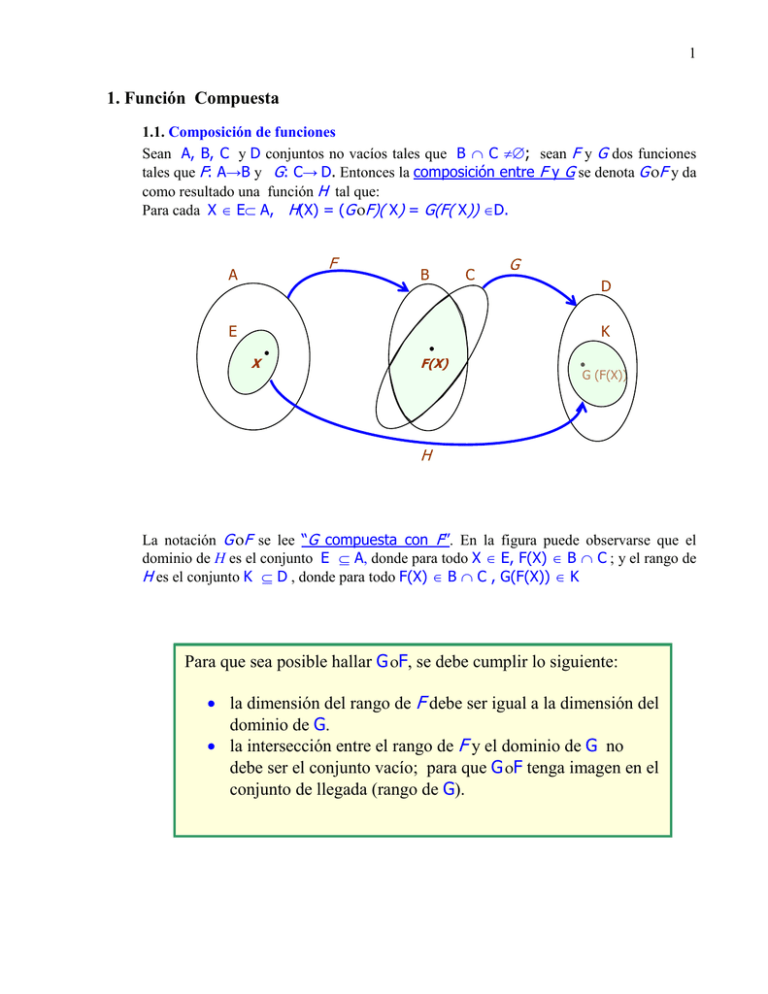
1
1. Función Compuesta
1.1. Composición de funciones
Sean A, B, C y D conjuntos no vacíos tales que B  C ; sean F y G dos funciones
tales que F: A→B y G: C→ D. Entonces la composición entre F y G se denota G F y da
como resultado una función H tal que:
Para cada X  E A, H(X) = (G F)( X) = G(F( X)) D.
F
A
B
C
G
D
K
E
X
F(X)
G (F(X))
H
La notación G F se lee “G compuesta con F”. En la figura puede observarse que el
dominio de H es el conjunto E  A, donde para todo X  E, F(X)  B  C ; y el rango de
H es el conjunto K  D , donde para todo F(X)  B  C , G(F(X))  K
Para que sea posible hallar G F, se debe cumplir lo siguiente:
 la dimensión del rango de F debe ser igual a la dimensión del
dominio de G.
 la intersección entre el rango de F y el dominio de G no
debe ser el conjunto vacío; para que G F tenga imagen en el
conjunto de llegada (rango de G).
2
La composición de funciones no cumple con la propiedad conmutativa.
No obstante, si cumple con la propiedad asociativa:
(H (G F)) (X) = H(G F(X))
= H(G(F(X)))
((H G) F))(X) = (H G)( F(X)) = H(G(F(X))),
y
(H (G F)) (X) = ((H G) F))(X) = (H G F)(X).
1.2. Continuidad de una función compuesta
Sea F: A→B una función continua en X0  A , y sea G : C→D tal que B C  una
función continua en F(X0)  B C . Sea H = G F.
F
A
G
B
D
C
E
G(F(X0))
F(X0)
X0



H
Como F es continua en X0 entonces
>0
existe un
lim F(X)  F(X 0 ) ,
X X0
lo que indica que dado un
 > 0 tal que:
F( X )  F( X 0 )  
Cuando
X  X0   .
3
Así mismo, Como G es continua en F(X0) entonces:
lim
F ( X )F ( X 0 )
G(F(X))  G( F(X 0 )) ,
lo que indica que dado un  > 0 existe un  > 0 tal que :
G( F( X ))  G( F( X 0 ))   Cuando F( X )  F( X 0 )   .
De donde G( F( X ))  G( F( X 0 ))   cuando X  X 0   , lo que es equivalente a
decir que
lim G(F(X))  G( F(X 0 ))
X X 0
Y permite afirmar que la función H = G F es continua en X0.
De la composición de dos funciones continuas en X0, resulta otra
función que también es continua en X0.
1.3. Teorema de la función compuesta
Sean F y G dos funciones tales que F: n → p es diferenciable en el elemento X0 y
G: p → m es diferenciable en el elemento F(X0). Entonces la función G ○ F: n → m
es diferenciable en el elemento X0 y se cumple que:
4
En caso que se tenga la compuesta de tres o más funciones que cumplan las condiciones del
teorema de la función compuesta el mismo puede aplicarse en forma reiterada. Por ejemplo,
si F: n → p es diferenciable en X0, G:p → q es diferenciable en F(X0) y H: q → m
es diferenciable en G(F(X0)) entonces, sobre la base de la propiedad asociativa de la
composición de funciones y el teorema de la función compuesta, para H G F: n → m
se tiene que:
Siendo
una matriz de “m” filas con “n” columnas.
1.4. Derivadas de orden superior de una función compuesta
Sea z = z(x,y) una función donde x = x(u,v) e y = y(u,v). Aplicando la regla de la cadena:
z z x z y


u x u y u
z
z
Donde
y
son funciones que dependen de x e y. Dado que x e y dependen de u y v,
x
y
z
z
entonces
y
son dependientes de x e y. Luego:
x
y
2z
  z    z x z y    z x    z y 





 

 
2
u  u  u  x u y u  u  x u  u  y u 
u
Sobre la base de las propiedades de las derivadas parciales:
 z 
 y 
 z 
 x 
 
 
 
 
  z x 
 x   x    u   z  ,   z y    y   y    u   z 
 


 
 
u  u 
u  y 
u  x u 
u  u 
u  x  u  y u 
z
z
Como
y
dependen de u y v, entonces:
x
y
 z 
 z 
 z 
   
 
2
2
 x    x  x   x  y   z x   z y
u
x u
y u x 2 u yx u
 z 
 z 
 z 
   
 
2
2
 y    y  x   y  y   z x   z y
u
x u
y u xy u y 2 u
5

Y en virtud que
u
2
  y   2 y
 x   x
, entonces:
  2 ,
 
u  u  u 2
 u  u
  z x    2 z x  2 z y  x    2 x  z 
   
 



u  x u   x 2 u yx u  u   u 2  x 
  z y    2 z x  2 z y  y    2 y  z 
   
 



u  y u   xy u y 2 u  u   u 2  y 
Al sustituir estas derivadas parciales en
2z
queda:
u 2
 2 z   2 z x  2 z y  x   2 x  z   2 z x  2 z y  y   2 y  z
 
 
 




u 2  x 2 u yx u  u  u 2  x  xy u y 2 u  u  u 2  y
Desarrollando y simplificando, se obtiene que:
 2 z  2 z  x 
 2 z y x  2 x z  2 z  y 
 2 z x y   2 y  z





  
  
yx u u u 2 x y 2  u 
xy u u  u 2  y
u 2 x 2  u 
2
2
En forma similar se obtiene el resto de las derivadas de segundo orden de z = z(x, y). Y
determinadas las derivadas de segundo orden puede determinarse, mediante el
procedimiento descrito, las derivadas de tercer orden y así sucesivamente. Todo lo expuesto
aquí es valido para una función de n en  .
Tomado de la guía “Diferenciación de Funciones Vectoriales”
Prof. Jesús Jiménez- Prof. E. Flores.