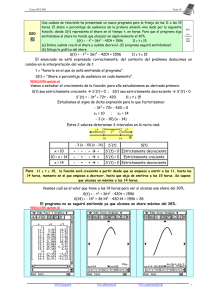
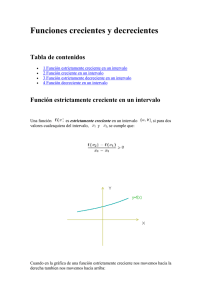
se dice que es estrictamente creciente cuando verifica que f`(x) > 0 y

Curso ON LINE
008
Tema 10
Dada la función f(x) = x3 - 81x2, calcula:
(a) Intervalos de crecimiento y decrecimiento.
(b) Puntos máximos y mínimos.
(c) Haz un esbozo de la gráfica de la función.
BH2
**
PAU
OVIEDO
Junio
1994
RESOLUCIÓN apartado a
Una función f(x) se dice que es estrictamente creciente cuando verifica que
estrictamente decreciente cuando verifica f'(x) < 0
f'(x) > 0 y
y' = 3x2 - 162x
Estudiamos el signo de esta nueva función derivada, para lo que factorizaremos el polinomio:
3x·(x - 54)
Comprobamos los valores que nos hacen cero cada uno de los factores:
x = 0
x = 54
Estos 2 valores determinan 3 intervalos en la recta real:
¿?
¿?
¿?
0
ℜ
54
3x·(x - 54)
y'
y
x<0
-·- → +
y' > 0
Estrictamente creciente
0 < x < 54
+·- → -
y' < 0
Estrictamente decreciente
x > 54
+·+ → +
y' > 0
Estrictamente creciente
La función es estrictamente decreciente para x < 0 ∨ x > 44
para 0 < x < 54
y estrictamente decreciente
RESOLUCIÓN apartado b
La función "y" alcanzará un máximo o un mínimo cuando y'= 0
y' = 3x2 - 162x = 3x·(x - 54) = 0
x1 = 0 ¿máximo o mínimo?
x1 = 54 ¿máximo o mínimo?
Para averiguarlo estudiamos la derivada segunda:
y'' = 6x - 162
y''(0) = 6 · 0 - 162 < 0 Máximo. (0, y)
y''(54) = 6 · 54 - 162 > 0 Mínimo. (54, y)
x = 0 Æ y = x3 - 81x2 = Æ y = 03 - 81·02 = 0
3
2
3
2
x = 54 Æ y = x - 81x = Æ y = 54 - 81·54 = - 78732
Æ (0, 0) Máximo
Æ (0, - 78732) Mínimo
RESOLUCIÓN apartado c
www.classpad.tk
www.abelmartin.tk
www.aulamatematica.tk
1