Conceptos Básicos de Funciones

Conceptos Básicos de Funciones
Definición.
Una función es una relación entre un conjunto de salida llamado dominio y un
conjunto de llegada llamado codominio, tal relación debe cumplir que cada
elemento del dominio se debe relacionar una vez con algún elemento del
codominio.
Ejemplos.
La relación anterior de nombre f es
una función, pues cumple que
todos los elementos del dominio se
están relacionando una vez con
algún elemento del codominio.
“g” es una función, pues cumple
que todos los elementos del
dominio se están relacionando una
vez con algún elemento del
codominio. A cada elemento del
dominio se le llama preimagen y a
cada elemento del codominio que
se relacione se le llama imagen.
El conjunto de las imágenes recibe el nombre de ámbito o rango de la función.
Si representamos el dominio de la función “g” con Dg, entonces
Dg = {1,2,3}
De forma similar Cg = {7,8,4,10,9} y Ag = {7,8}.
Prof. Jonathan Brenes.
Página 1
La relación “h” no es una función,
pues el 3 es un elemento del
conjunto de salida que no se está
relacionando. No es de importancia
que el 4 del conjunto de llegada no
se relacione, pues en éste conjunto
pueden
sobrar
elementos
sin
relacionarse.
La relación “f” no es una función, pues
el 2 debió relacionarse una sola vez.
La forma de relacionar los elementos en una función está dada por una regla
llamada criterio de la función.
Ejemplo:
Observe que cada elemento del
dominio se relaciona con su doble; el
doble de 0 es 0, el de 1 es 2, etc. Si “x”
representa el valor de un elemento del
dominio entonces “x” se relaciona con
el número “2x” en el codominio.
Lo cual se escribe
, y significa
que en la función
cada vez que se
toma un valor
del
se relacionará
con
en el .
A cada elemento del ámbito se le suele
representar con la letra “ .
Prof. Jonathan Brenes.
Página 2
Una definición más formal de una función es la siguiente.
Definición: Se define una función
.
como
con la condición
Otras definiciones.
Par ordenado: Un par ordenado es una expresión de la forma
e
.
Gráfico: Es el conjunto de pares ordenados, se representa con
anterior el gráfico es.
donde
, en la función
Gráfica: Es la representación del gráfico en un plano cartesiano.
Un plano cartesiano es la intersección perpendicular de un eje
cada uno con una métrica.
Prof. Jonathan Brenes.
con un eje ,
Página 3
Gráfica de la función anterior.
Sin embargo hay funciones que están conformadas por infinitos puntos unos tras
otros, por ejemplo.
No todas las gráficas corresponden a funciones, en la gráfica siguiente el
se está relacionando dos veces, con el y con el
del eje .
Prof. Jonathan Brenes.
del eje
Página 4
Observe lo anterior en un diagrama de Venn
Análisis de gráficas.
Dominio: Para determinar el dominio de una función desde su gráfica se debe
observar cuáles números del eje abarca la gráfica.
Ejemplo:
El dominio de la función son todos
los números desde el -4 hasta el 1.
El dominio siempre se lee en el eje
de izquierda a derecha.
Prof. Jonathan Brenes.
Página 5
Ámbito: Para determinar el ámbito se debe observar cuáles números del eje
abarca la función.
En la función anterior
El ámbito siempre se lee de abajo hacia arriba en el eje .
Otros ejemplos.
El corchete abierto es
porque
el
“punto
abierto” (4,1) no es
parte del gráfico de la
función.
La flecha indica que la
gráfica no tiene un
origen. Los “infinitos”
llevan siempre los
corchetes abiertos.
Prof. Jonathan Brenes.
Página 6
El intervalo
equivale a todos los
números reales.
La gráfica de ésta función está compuesta por dos segmentos disjuntos, observe
que los números del eje que están entre -1 y 3 no se están relacionando.
Prof. Jonathan Brenes.
Página 7
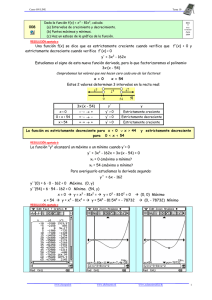
Intervalos de Monotonía.
Consiste en determinar los intervalos del eje donde la función es estrictamente
decreciente, constante o estrictamente creciente.
La monotonía se lee en el eje x de izquierda a derecha, suponga entonces que la
función anterior representa un camino para una persona que camina de izquierda
a derecha.
La parte que es de subida toma en cuenta los valores del eje x que van de -5
hasta el -2, y es donde la función es estrictamente creciente; la parte llana toma en
cuenta los valores de -2 hasta el 3, y corresponde a la parte donde la función es
constante; la parte de bajada va desde el 3 hasta el 5, y es donde la función es
estrictamente decreciente.
Prof. Jonathan Brenes.
Página 8
Por lo que la función
Es estrictamente creciente en
Es constante en
Es estrictamente decreciente en
También se dice que la función es creciente en el intervalo donde no es
estrictamente decreciente, y es decreciente donde la función no es estrictamente
creciente.
Con lo que tenemos





es estrictamente creciente en
es creciente en
es constante en
es estrictamente decreciente en
es deciente en
Observe que los corchetes en la monotonía se utilizan siempre abiertos.
Ejemplos
es estrictamente creciente en
no es constante ni estrictamente decreciente, por lo que se dice que
estrictamente creciente en todo su dominio.
Prof. Jonathan Brenes.
es
Página 9