ANÁLISIS MATEMÁTICO I Trabajo Práctico Nº 5: Derivadas 1
Anuncio
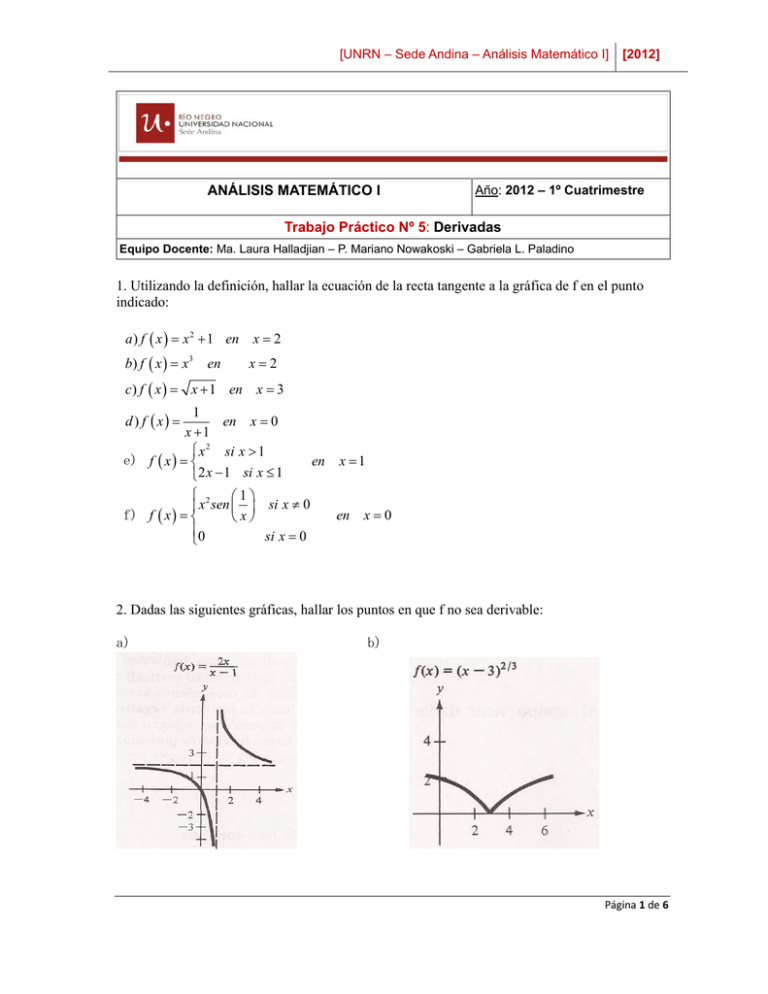
[UNRN – Sede Andina – Análisis Matemático I] ANÁLISIS MATEMÁTICO I [2012] Año: 2012 – 1º Cuatrimestre Trabajo Práctico Nº 5: Derivadas Equipo Docente: Ma. Laura Halladjian – P. Mariano Nowakoski – Gabriela L. Paladino 1. Utilizando la definición, hallar la ecuación de la recta tangente a la gráfica de f en el punto indicado: a ) f ( x ) = x 2 + 1 en x = 2 b) f ( x ) = x 3 en x=2 c) f ( x ) = x + 1 en x = 3 1 en x = 0 x +1 ⎧ x 2 si x > 1 e) f ( x ) = ⎨ ⎩2 x − 1 si x ≤ 1 d ) f ( x) = ⎧ 2 ⎛1⎞ ⎪ x sen ⎜ ⎟ si x ≠ 0 f) f ( x ) = ⎨ ⎝x⎠ ⎪0 si x = 0 ⎩ en x =1 en x=0 2. Dadas las siguientes gráficas, hallar los puntos en que f no sea derivable: a) b) Página 1 de 6 [UNRN – Sede Andina – Análisis Matemático I] c) [2012] d) 3. Hallar la ecuación de una recta que sea tangente a la gráfica de y = x2 y sea paralela a la recta 3x – y + 1 = 0. 4. Hallar la ecuación de una recta que sea tangente a la gráfica y = 1 x y sea paralela a la recta x + 2y – 6 = 0. 5. ¿En qué puntos de la gráfica de la función f ( x ) = x 2 − 6 x + 8 la recta tangente es paralela al eje de las x? 6. Utilizando las técnicas de derivación, hallar la derivada de la función dada: a) f ( x ) = 3 i ) f ( x ) = x 2 ln x b) f ( x ) = x + 3 f ) f ( x) = xe x sin x − cos x sin x + cos x e x + e− x k ) f ( x ) = cosh x = 2 x e − e− x l ) f ( x ) = sinh x = 2 x e + x m) f ( x ) = 2 x2 + 1 n) f ( x ) = ( ln x ) e x ( x + 1) g ) f ( x ) = ( x 2 + 1) .ln x o) f ( x ) = c) f ( x ) = x 2 + 4 d ) f ( x ) = 5 x3 − 3 x 2 + 14 e) f ( x ) = cos x − sin x h) f ( x ) = xe x x2 + 2 j) f ( x ) = 1 3 − x x2 p ) f ( x ) = tan x Página 2 de 6 [UNRN – Sede Andina – Análisis Matemático I] [2012] 7. Calcular la derivada de cada una de las siguientes funciones en el punto dado: 1⎞ 1 1 7 ⎛ a) f ( x) = (0; 1) b) f ( x) = − + x 2 ⎜ 0;− ⎟ 2⎠ x 2 5 ⎝ 2⎞ 3 ⎛3 ⎞ ⎛ d) f ( x) = 3x⎜ x 2 − ⎟ (2;18) c) f (t ) = 3 − ⎜ ;2 ⎟ x⎠ 5t ⎝ 5 ⎠ ⎝ e) f (x) = (2x + 1)2 (0; 1) f) f (x) = 3(5 – x)2 (5; 0) g) f ( ϑ ) = 4senϑ − ϑ (0; 0) h) g (t) = 2 + 3cost (π; -1) 8. Hallar f’ (x): a) f ( x) = x 2 − 4 x b) f (x) = x2 – 3x – 3x-2 + 5x-3 2 c) f ( x) = x − 3 x − 4 x e) f (x) = x(x2 + 1) x 3 − 3x 2 + 4 d) f ( x) = x2 4/5 f) f (x) = x g) f ( x) = 3 x + 5 x h) f ( x) = 4 x + 3 cos x i) f (x) = 2senx + 3cosx 1 k) f ( x) = 3 x2 x +1 m) f ( x) = x 3 o) h( x) = x x + 3 j) f (x) = (x2 + 2x)(x + 1) 3t − 2 l) h(t ) = 2t − 3 3 ( q) f ( x) = ) x +c x2 − c2 2 2 2 ⎞ ⎛ n) f (t ) = t 4 ⎜1 − ⎟ ⎝ t +1⎠ p) f (x) = (3x3 + 4x)(x – 5)(x + 1) r) h(t ) = t (t 2 − 1) t +3 9. Para cada una de las siguientes funciones, hallar los puntos (si los hay) en los que la función propuesta tiene tangente horizontal: 1 a) y = x4 – 3x2 + 2 b) y = x + sen x 0 ≤ x < 2π c) y = 2 x 10. Para cada una de las siguientes funciones, hallar f’ (x) y f’ (c) para el valor de c indicado. 1 5 − 6x 2 a) f ( x) = (2 x 3 − 4) , c = 0 , c=1 b) f ( x) = 3 7 c) f (x) = 5x-2(x + 3) , c = 1 d) f (x) = (x2 – 2x + 1)(x3 – 1) , c = 1 1 f) f ( x) = x 2 − 3x 2 , c = -1 e) f (x) = (x3 – 3x)(2x2 + 3x + 5) , c = 0 x x +1 , c=2 g) f ( x) = x −1 ( ) Página 3 de 6 [UNRN – Sede Andina – Análisis Matemático I] [2012] 11. Hallar la derivada de las siguientes funciones aplicando la regla de la cadena: 3 f ( x) = (2 + x) f ( x) = (2 + x) 200 f ( x) = (2 + x) n f ( x ) = e x +3 f ( x ) = 1 + tan 2 x f ( x ) = cos ( 3 x ) f ( x ) = 3sin 4 ( x ) f ( x ) = ln ( 3 x + 1) f ( x ) = ln (1 + cos x ) f ( x ) = ( 4 sen 2 x ) − ( sin x ) −1 −1 f ( x ) = sin 2 x + cos 2 x ( 2 x + 5) f ( x) = ln ( x + 1) 2 3 2 f ( x ) = esin x − cos3 x 2 f ( x ) = ln ( 5 x ) − ln ( 3 x ) f ( x ) = esin x − cos3 x 2 ( f ( x ) = ln ( x 2 + 1) ) 1 2 12. Hallar dy/dx : a ) x 2 + y 2 = 16 b) xy = 4 1 1 x2 − 9 x2 + 9 f ) x3 y 3 − y = x e) y 2 = c) x 2 + y 2 = 9 g ) ( x − y ) = x3 − y 3 d ) x3 − xy − y 2 = 9 h) xy = x − 2 y 3 Página 4 de 6 [UNRN – Sede Andina – Análisis Matemático I] [2012] 13. Calcular la derivada de las siguientes funciones: a) f ( x ) = x x d ) f ( x) = xx b) f ( x ) = x 4 x + a x c) f ( x ) = ( sen x ) 3 e) f ( x ) = (1 + senx ) a>0 1⎞ ⎛ f ) f ( x) = ⎜ x + ⎟ x⎠ ⎝ ln x cos x x 14. Sean f y g funciones tales que f ( x ) = 1 + x 2 , g `( x ) = sen 2 ( sen (1 + 3 x ) ) ; g `( 0 ) = 4; h ( x ) = g (1 + 2 x ) . Calcular ( f o g )´( 0 ) y ( h o f )´( 0 ) . 15. Para cada una de las siguientes funciones: a) Realizar un gráfico, b) Estudiar la continuidad y la derivabilidad en el punto indicado. c) Para aquellas que resulten derivables, hallar la ecuación de la recta tangente en el punto indicado. a) f ( x ) = x − 1 en x = 1 ⎧0 si x < 2 b) f ( x ) = ⎨ en x = 2 ⎩ x − 2 si x ≥ 2 ⎧ ⎛1⎞ ⎪ xsen ⎜ ⎟ si x ≠ 0 c) f ( x ) = ⎨ en x = 0 ⎝ x⎠ ⎪0 si x = 0 ⎩ ⎧ 2 ⎛1⎞ ⎪ x sen ⎜ ⎟ si x ≠ 0 d) f ( x ) = ⎨ ⎝ x⎠ ⎪0 si x = 0 ⎩ 16. Sea f : → en x = 0 / f ( x ) = 6e x +3 x , 3 a) mostrar que f ´( x ) > 0 para todo x, b) Utilizando el Teorema de la función inversa, analice la existencia de ( f −1 )´( 5 ) y, calcule su valor. 17. Sea f : [ −1; +∞ ) → / f ( x) = −x − x +1 a) Analizar el signo de f ´( x ) para todo x, b) Utilizando el Teorema de la función inversa, analice la existencia de ( f −1 )´( 5 ) y, calcule su Página 5 de 6 [UNRN – Sede Andina – Análisis Matemático I] [2012] valor. 18. Sea f : / f ( x ) = sinh x = → a) mostrar que f ´( x ) > 0 para todo x, e x − e− x , 2 b) Utilizando el Teorema de la función inversa, analice la existencia de ( f −1 )´( x ) . Calcule ( f )´( 0 ) = ( sinh ) ( 0 ) . −1 −1 19. La ley de movimiento de un punto a lo largo de una recta es s ( t ) = 6t − 2t 2 . Hallar la velocidad de movimiento del punto para t=0, t=1; t=2. 20. Un objeto circular va aumentando su tamaño con el tiempo. El radio r, en centímetros viene dado por r = 9t + 6, donde t representa el tiempo en minutos. a) ¿Cuál es la velocidad de crecimiento del radio? b) ¿Cuál es la velocidad de variación del área? 21. El área de un triángulo equilátero disminuye a razón de 4cm2 /min. Encuentre la razón de cambio de la longitud de sus lados en el momento en que el área del triángulo es de 200cm 2 . Página 6 de 6