UNRN-AM I 2012 - TP 2 Funciones

[UNRN – Sede Andina – Análisis Matemático I]
ANÁLISIS MATEMÁTICO I
[2012]
Año: 2012 – 1º Cuatrimestre
Trabajo Práctico Nº 2: Funciones
Equipo Docente: Ma. Laura Halladjian – P. Mariano Nowakoski – Gabriela L. Paladino
1.
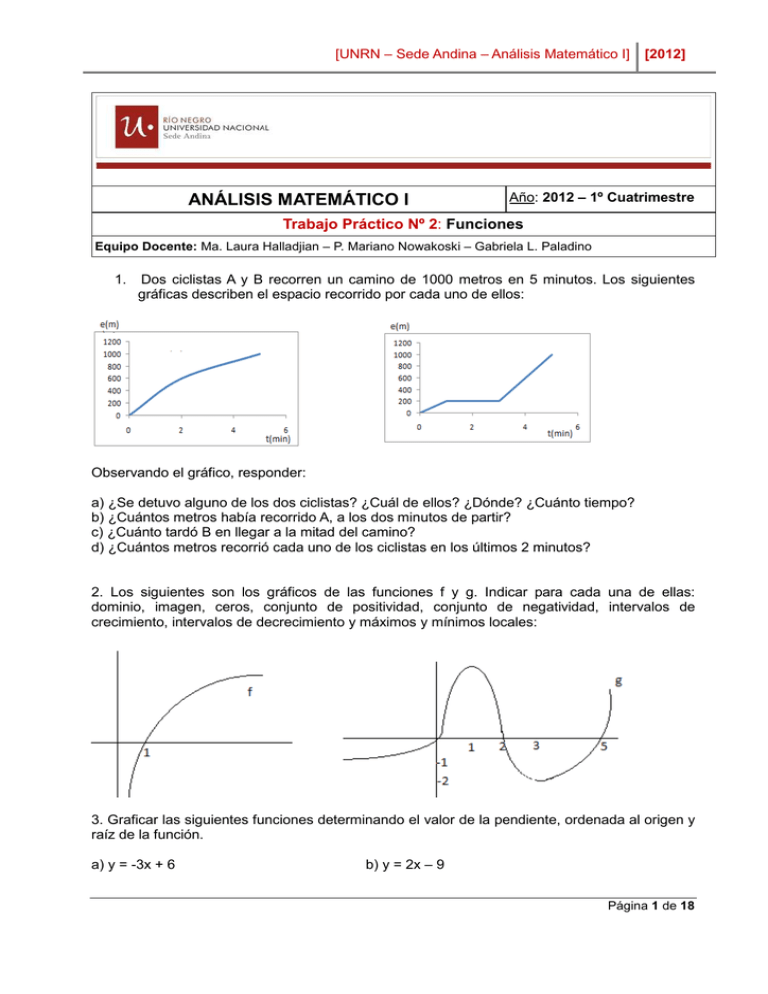
Dos ciclistas A y B recorren un camino de 1000 metros en 5 minutos. Los siguientes
gráficas describen el espacio recorrido por cada uno de ellos:
Observando el gráfico, responder:
a) ¿Se detuvo alguno de los dos ciclistas? ¿Cuál de ellos? ¿Dónde? ¿Cuánto tiempo?
b) ¿Cuántos metros había recorrido A, a los dos minutos de partir?
c) ¿Cuánto tardó B en llegar a la mitad del camino?
d) ¿Cuántos metros recorrió cada uno de los ciclistas en los últimos 2 minutos?
2. Los siguientes son los gráficos de las funciones f y g. Indicar para cada una de ellas:
dominio, imagen, ceros, conjunto de positividad, conjunto de negatividad, intervalos de
crecimiento, intervalos de decrecimiento y máximos y mínimos locales:
3. Graficar las siguientes funciones determinando el valor de la pendiente, ordenada al origen y
raíz de la función.
a) y = -3x + 6
b) y = 2x – 9
Página 1 de 18
[UNRN – Sede Andina – Análisis Matemático I]
c) y = – 4
e) y =
d) y = -3x – 8
1
x–5
2
f) y = 0
4. Indicar si los siguientes puntos pertenecen a la recta y =
(0;0)
[2012]
(3;0)
(-1/2; 1/6)
1
x–1
3
(3/2; 2)
5. Dado el siguiente gráfico:
a) ¿Cuánto vale la función cuando x = 0?
b) ¿Para qué valor de x la función vale 0?
c) Determinar la ecuación de la recta graficada.
6. Para cada una de las siguientes rectas, determinar el valor de la pendiente y el de la
ordenada al origen:
7. Si una recta pasa por los puntos (0;3) y (1; 6), ¿cuánto vale su ordenada al origen? ¿Cuál es
el valor de la pendiente? Determinar la ecuación de la recta.
8. Graficar la recta cuya pendiente vale 5 y cuya raíz vale –2. Encontrar su ecuación.
9. Encontrar la ecuación de una recta sabiendo que su pendiente vale –4 y pasa por el punto
(2; -5).
10. Encontrar la ecuación de una recta sabiendo que pasa por el punto (-2; 6) y su ordenada al
origen vale –3.
Página 2 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
11. Los siguientes gráficos representan el espacio recorrido por móviles que se desplazan con
movimiento rectilíneo uniforme en función del tiempo:
a) ¿Cuáles de ellos tienen velocidad positiva y cuáles velocidad negativa?
b) ¿Cuál es el más veloz de los que avanzan y cuál es el más veloz de los que retroceden?
c) ¿Qué le sucede al móvil 4?
12. Si r ( t ) = 2t + 3 describe, en función del tiempo, el espacio recorrido por un móvil que se
desplaza con movimientos rectilíneo uniforme, expresar y representar en un sistema de
coordenadas
a) El espacio recorrido por otro móvil que se desplaza a igual velocidad y que está tres
unidades de distancia adelantado.
b) El espacio recorrido por oto móvil que se desplaza al doble de velocidad y en el instante
t = 0 se encuentra en el mismo punto que el primero.
c) El espacio recorrido por otro móvil que se desplaza con la misma velocidad pero en sentido
contrario y parte en t = 0 del mismo punto que el primero.
2
13. Trazar el gráfico de las siguientes funciones cuadráticas a partir de f ( x ) = x indicando
cómo se modificó la curva original:
2
a) f ( x ) = 2 x
e) f ( x ) = ( x − 1)
2
b) f ( x ) = −2 x
2
2
g) f ( x ) = x − 1
1 2
x
2
2
h) f ( x ) = x + 1
c) f ( x ) =
−1 2
x
2
2
i) f ( x ) = ( x + 1)
d) f ( x ) =
Determinar en cada caso el conjunto imagen, las raíces, los intervalos de crecimiento y
decrecimiento.
14. Graficar las siguientes funciones indicando en cada caso intervalos de crecimiento, de
decrecimiento, conjuntos de ceros, positividad y negatividad.
a) f ( x ) = 2 x ( x − 1)
2
e) f ( x ) = x − 5 x + 6
b) f ( x ) = −2 x ( x + 3)
c) f ( x ) = 2 ( x + 3)( x − 1)
2
d) f ( x ) = x + 2 x + 1
Página 3 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
15.- Una función cuadrática tiene una expresión de la forma y = x² + ax + a y pasa por el punto
(1, 9). Calcular el valor de a.
16. Se sabe que la función cuadrática de ecuación y = ax² + bx + c pasa por los puntos (1,1),
(0, 0) y (-1,1). Calcular a, b y c.
17. Una parábola tiene su vértice en el punto V(1, 1) y pasa por el punto (0, 2). Halla su
ecuación.
18. El conjunto de ceros de la función f es
{−3; 4} y el conjunto imagen es
Im f = [ −2; +∞ ) .
Hallar la fórmula de f.
19. Indicar cuál de las funciones siguientes corresponde a cada uno de los gráficos:
2
a) f1 ( x ) = x − 4 x + 4
c) f3 ( x ) = − x 2 + 3 x − 3
1 2 2
x − x−2
3
3
2
d) f 4 ( x ) = −2 x + 12 x − 2
b) f 2 ( x ) =
Página 4 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
20. Hallar, analítica y gráficamente los puntos de intersección de las siguientes funciones:
a) f ( x ) = 2 x − 7 x − 15
2
b) f ( x ) = 3x + 5 x − 7
2
c) f ( x ) = −3x + 5 x − 9
2
;
g ( x ) = 3x + 1
g ( x ) = −7 x + 8
;
;
g ( x ) = 2x + 9
21. A continuación se indica cuántas unidades y en qué dirección debe trasladarse la siguiente
gráfica:
i) dos hacia arriba, 2 a la izquierda.
ii) 3 hacia abajo
a) Dar la ecuación para la gráfica trasladada y graficar la misma en el gráfico de referencia.
b) Indicar si la función de referencia y la trasladada es par, impar o ninguna de las dos.
22. Un proyectil se dispara verticalmente hacia arriba. Su altura (en metros) sobre el suelo está
2
dada por h ( t ) = −5t + 10t .
a) ¿Para qué valores de t el proyectil asciende? ¿Para cuáles desciende?
b) Hallar el instante en que el proyectil alcanza la altura máxima y calcularla.
c) Hallar el tiempo que demora el proyectil en llegar al suelo.
d) Si otro proyectil es disparado en iguales condiciones, pero a 50 metros del suelo, hallar su
altura sobre el suelo t segundos después del disparo. Resolver a), b) y c) para este caso.
23. Encontrar el punto perteneciente a la recta de ecuación y = 3 x − 1 más cercano al punto
P = ( 4;1) .
24. Dos fabricantes de cierto artículo con una producción x (en miles de unidades) obtienen
respectivamente una ganancia (en miles de pesos) de:
p1 ( x ) = − x 2 + 4 x − 3
y
p2 ( x ) = x − 13 .
Página 5 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
a) Graficar ambas funciones de ganancia.
b) ¿Cuántas unidades deben producir ambos fabricantes para obtener la misma ganancia?
c) ¿Para qué producción las ganancias obtenidas por el primer fabricante cuadruplican las
del segundo?
25. Un constructor debe hacer una ventana rectangular. Para el marco dispone de 6,40 metros
de varilla metálica. Hallar las dimensiones de modo que el área de abertura sea máxima.
26. Representar gráficamente las siguientes funciones a partir de la función
f ( x ) = x3
analizando el crecimiento en cada caso:
a) f ( x ) = − x
b) f ( x ) = x − 1
3
3
c) f ( x ) = x + 1
3
d) f ( x ) = ( x − 1) .
3
27. A continuación se indica cuántas unidades y en qué dirección debe trasladarse la siguiente
gráfica:
i) 4 hacia arriba, 4 a la izquierda.
ii) 4 hacia abajo, 2 a la derecha.
a) Dar la ecuación para la gráfica trasladada y graficar la misma en el gráfico de referencia.
b) Indicar si la función de referencia y la trasladada es par, impar o ninguna de las dos.
4
3
2
28. Dada la función g ( x ) = 4 x + 2 x − 30 x − 36 x , encontrar todos los puntos donde g corta al
eje x sabiendo que x=3 es una raíz de g.
29. Indicar la función que corresponde a cada gráfica:
a) y = ln (x – 1) + 2
d) y =
1
(x + 1)2
+2
g) y = (x + 1)2 – 2
b) y = x − 1 - 2
c) y = (x – 2)2 + 3
e) y = 1 + cos x
f) y = 1 – sen x
h) y = ln (x + 2) – 3
i) y =
x − 2 +1
Página 6 de 18
[UNRN – Sede Andina – Análisis Matemático I]
j) y =
1
−1
( x − 2) 2
k) x + 2 + 3
l)
[2012]
x + 2 −1
Página 7 de 18
[UNRN – Sede Andina – Análisis Matemático I]
30. Hallar una función polinómica h de grado 3 cuyas raíces sean x=3, x=-1 y x=
[2012]
−1
.
2
31. Graficar las siguientes funciones. Indicar dominio, imagen, intervalos de crecimiento,
paridad e imparidad:
a) f (x) = -x2 + 6x – 7
c) f (x) =
−2
+4
x −1
e) f (x) = x - x
x
x
g) f 8x) =
i) f (x) =
k) f (x) =
m)
x2 −1
x −1
3
x + 2 −1
b) f (x) =
d) f (x) =
6 − 2x
−4
+1
( x + 1) 2
f) f (x) = 2 x − 3
h) f (x) = x 2 − 1
j) f (x) = -(x – 1)3 + 2
l) f (x) = x − 2
n)
Página 8 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
32. Sea f una función polinómica tal que sus únicas raíces son x-1, x=2 y x=4. Además se
sabe que f ( 0 ) = 1, f ( −2 ) = −12, f ( 3) = 0,5, f ( 5) = −12. Hallar los intervalos de positividad y
negatividad de f.
33.
Un meteorólogo halló que la temperatura (en ºC) durante cierto día estaba dada por
C (t ) =
1
( t − 12 )( t − 24 ) t donde t es el tiempo medido en horas, a partir de las 6 de la
200
mañana:
a)¿Cuándo se registraron temperaturas por encima de de 0º C?
b)¿Cuándo se registraron temperaturas por debajo de de 0º C?
c)¿En algún momento del día se registro una temperatura de 32º C? ¿Cuándo?
34. Graficar las siguientes funciones indicando previamente el dominio de cada una de ellas.
En cada caso indicar ecuaciones de las asíntotas, ceros, intervalos de crecimiento y de
decrecimiento y conjunto imagen:
a) f ( x ) =
2
x
b) f ( x ) = −
e) f ( x ) =
x −3
2x +1
f) f ( x ) =
35. Dadas las funciones
2
x
c) f ( x ) =
2
x −1
d) f ( x ) =
2
+3
x −1
2x − 3
3x + 4
f ( x) =
1
x −1 ,
2
g ( x ) = x2 − 1 y
h( x) =
1
+ 2 , calcular
−1 + x
f o g , g o f , f o h, h o f , g o g , g o h. y el dominio de cada una de las composiciones.
36. Sean f ( x ) = 2 x − 3 y g ( x ) =
3
+ 2 hallar las funciones f o g , g o f , el dominio de
x−2
ambas composiciones y en caso de existir, las ecuaciones de las asíntotas de cada
composición.
37. Dadas las funciones f ( x ) = ax − 2 y g ( x ) =
g o f ( 2) = 0
38. Dada la función
x −3
hallar el valor de a para que
2x −1
f, calcular su dominio, calcular f −1 y su dominio y verificar que
f o f −1 = f −1 o f = x.
a) f ( x ) = 2 x − 3
3
x−2
x −3
c) f ( x ) =
4x − 2
b) f ( x ) =
Página 9 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
39. La relación funcional entre grados Celsius y grados Kelvin es lineal. Sabiendo
que
0o C = 273o K y que 27o C = 300o K , encontrar la función f que da la temperatura en grados
Celsius conocida la misma en grados Kelvin.
40. La función g ( x ) = 1,8 x + 32 expresa la temperatura en grados Fahrenheit, conocida la
misma en grados Celsius; encontrar la expresión de la temperatura en grados Fahrenheit en
función de la temperatura en grados Kelvin. ¿Es lineal?
41. La función g ( x ) = 1,8 x + 32 expresa la temperatura en grados Fahrenheit, conocida la
misma en grados Celsius. Encontrar la función que permite, dada una temperatura en grados
Fahrenheit, obtener la misma en grados Celsius.
42. Determinen si son verdaderas o falsas las siguientes afirmaciones. Justificar las
respuestas. En todos los casos, a es un número real positivo.
a) a ⋅ a = a
n
) a −n =
n +1
b) a ⋅ a = a
n
1
a −n
n
g) a − n =
p
q
c) a =
2
( a)
q
p
d) a n : a = a n −1
e) a −1 =
1
f
a
1
an
43. Completar la siguiente tabla:
X
y=2
4
3
2
1
0
-1
-2
-3
-4
x
a) Graficar
b) Indicar el dominio, la imagen y la asíntota. Decir si la función es creciente o decreciente.
Justificar.
44. Completar la siguiente tabla:
X
4
1
y= 
2
3
2
1
0
-1
-2
-3
-4
x
a) Graficar la función en el mismo sistema de coordenadas que la función del ejercicio anterior.
¿Cómo resultan sus gráficas?
b) Indicar el dominio, la imagen y la asíntota. Decir si la función es creciente o decreciente.
Justificar.
45. Construir la tabla de valores y graficar:
i) y = 5 x
1
ii ) y =  
4
x
a) Indicar la ecuación de la función simétrica respecto al eje y.
b) Indicar la imagen y la asíntota de cada una. Decir si las funciones son crecientes o
decrecientes. Justificar.
Página 10 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
46. Completar la siguiente tabla y graficar:
x
4
y=2
3
2
1
0
-1
-2
-3
-4
x
y = 3⋅ 2 x
a) Indicar la imagen y la asíntota. Decir si la función es creciente o decreciente. Justificar.
b) Construir la tabla de valores para cada una de las siguientes funciones y graficarlas en el
mismo sistema de coordenadas.
i) y =
1 x
⋅3
3
1
iii ) y = − ⋅ 3 x
3
ii ) y = -3 ⋅ 3 x
iv) y = 3 ⋅ 3 x
c) Indicar la imagen y la asíntota de cada función. Decir si las funciones son crecientes o
decrecientes. Justificar.
47. Completar la siguiente tabla y graficar:
X
4
y=2
3
2
1
0
-1
-2
-3
-4
x
y = 1+ 2 x
a) Indicar la imagen y la asíntota. Decir si la función es creciente o decreciente. Justificar.
b) Construir la tabla de valores y graficar en los mismos ejes:
i ) y = −1 + 2
x
1
ii ) y = −3 +  
2
x
iii ) y = 2 + 2 x
d) Indicar la imagen y la asíntota de cada una. Decir si las funciones son crecientes o
decrecientes. Justificar.
48. Graficar las siguientes funciones:
1
i ) y = −2 + ⋅ 3 x
3
1
ii ) y = − ⋅ 2 x + 3
4
1
iii ) y =  
 10 
x
a) Indicar la imagen y la asíntota de cada función. Decir si las funciones son crecientes o
decrecientes. Justificar.
49. Para cada una de las siguientes funciones:
i) f (x) = 2.3x – 5
ii) f (x) = 4 – 2.4x
1
2
x
iii) f (x) = 3 +  
determinar:
a) La asíntota.
b) El dominio.
c) El crecimiento o decrecimiento.
d) El punto donde corta al eje de las y.
Página 11 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
50. Hallar la fórmula de la función exponencial del tipo f (x) = k.ax, que verifique las condiciones
pedidas en cada caso:
a) Su base es 2/3 y su coeficiente es 40.
b) Pasa por el punto (3; 64/25) y corta al eje de las y en 5.
c) Pasa por el punto (-1; 3/2) y k = 2.
d) a = 0,5 y corta al eje de las y en 4.
51. Considerar las funciones f (x) = 30.(1/3)x y g (x) = 0,2.4x.
a) Hallar f (-2) y g (3/2).
b) Indicar, si es posible, para que valores de x se cumple que:
i) f (x) = 10
ii) f (x) = -10
iii) g (x) = 0
iv) g (x) = 16/5
52. El aire de una fábrica es filtrado de tal modo que la cantidad de contaminantes decrece de
acuerdo a P = P0 e-kt donde t representa el tiempo en horas. Si el 10% de los contaminantes es
removido en las primeras 5 horas:
a) ¿Qué porcentaje de contaminantes hay después de 10 horas?
b) ¿En qué tiempo los contaminantes se reducirán 50%?
53. Hallar una fórmula que describa el crecimiento exponencial de una población que aumenta
el 12% cada 5 años, considerando una cantidad inicial de 55 millones de habitantes.
54. Un procedimiento para averiguar la edad de un fósil consiste en analizar la proporción que
este posee de carbono-12 y carbono-14. Cuando un organismo muere, el carbono-12 perdura
casi inalterable, mientras que el carbono-14 se desintegra con el paso del tiempo por ser
radiactivo.
La variación de la masa de cierta cantidad de carbono-14 a través del tiempo puede calcularse,
aproximadamente, a través de la fórmula:
M = M0.0,886t
Donde M0 es la masa inicial (en gramos), t es el tiempo en miles de años y M es la masa de
carbono que queda (en gramos).
a) Calcular el porcentaje aproximado de la masa de carbono-14 que se conserva al cabo de
11460 años en un fragmento de un fósil de un organismo que, en vida, contenía 250g.
b) Repetir el cálculo para una masa inicial de 820g.
c) Suponiendo que la variación de la masa de una sustancia radiactiva se produce según la
función:
M = M0.0,5t
Indicar si su desintegración es más rápida o más lenta que la del carbono-14.
Página 12 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
55. Dada la función y = log 3 x
a) Completar la siguiente tabla de valores:
x
27
y = log 3 x
9
3
1
1/3
1/9
1/27
b) Graficar.
c) Determinar el dominio de la función.
d) Determinar la asíntota de la función.
e) Determinar si la función es creciente o decreciente.
f) ¿En qué punto la curva corta al eje x?
56. Dada y = log 1/3 x
a) Construir una tabla de valores conveniente.
b) Graficar la función.
c) Determinar su crecimiento o decrecimiento.
d) ¿En qué punto la curva corta al eje x?
57. Dada y = log 4 x
a) Construir una tabla de valores conveniente.
b) Graficar la función.
c) Determinar su crecimiento o decrecimiento.
d) ¿En qué punto la curva corta al eje x?
58. Dadas las funciones:
i) y = 2. log 3 x ii) y = -2. log 3 x
iii) y = 3. log 2 x
iv) y = - log 2 x
a) Graficarlas
b) Determinar el crecimiento o decrecimiento de cada una. Extraer conclusiones.
c) Determinar la asíntota de cada función.
59. Dadas las funciones:
i) y = log 2 (x – 1)
ii) y = log 2 (x + 2)
iii) y = log 3 (x – 3)
iv) y = log 3(x + 4)
a) Construir una tabla de valores conveniente para cada función.
b) Graficarlas.
c) Determinar el dominio de cada una.
d) Determinar la asíntota de cada una.
e) ¿En qué punto cada curva corta al eje x?
60. Teniendo la función y = log 2 (x + 6), determinar sin graficar:
a) Su asíntota.
b) Su dominio.
c) El crecimiento o decrecimiento de la función.
d) El punto donde la curva va a cortar al eje x.
Página 13 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
61. Teniendo la función y = log 4 (x – 7), determinar sin graficar:
a) Su asíntota.
b) Su dominio.
c) El crecimiento o decrecimiento de la función.
d) El punto donde la curva va a cortar al eje x.
62- La escala de Richter, utilizada para medir la intensidad de los terremotos, es una escala
logarítmica de base 10.
La magnitud de un terremoto en esa escala está dada por la fórmula:
M = log p
Donde M es el grado en la escala de Richter y p es la potencia que indica cuántas veces mayor
fue la onda sísmica del terremoto en comparación con una onda de referencia correspondiente
a la situación normal.
En 1906, un terremoto en la ciudad de San Francisco tuvo una magnitud de 8,2 en la escala de
Richter. En 1989 hubo otro, que fue 19,95 veces más potente que el de 1906.
a) Hallar el grado en la escala de Richter del terremoto de 1989.
63. Utilizando la circunferencia trigonométrica, completar la siguiente tabla:
X
0 π/6
π/4
π/3
π/2
2
5
π - π
3
6
5
π
2
11
π
3
5
π
4
17
π
π −
6
3
7
π
6
Sen x
Cos x
64. Para cada una de las siguientes funciones en el intervalo indicado, hallar todos los ceros y
los conjuntos de positividad y negatividad:
a) f (x) = 1 + 2senx
en [0;2π]
b) f (x) = 3 – 4cos2 x
en [π; 2π]
c) f (x) = cos (x – π/4) en [0; 5π]
d) f (x) = sen (2x – π/4) en [0; 3π]
e) f (x) = 1 – 2cos(4x – π) en [-π; π]
f) f (x) = 2sen(x/4 + π) -
65. Sea g (x) = 2 -
2
en [0; 5π]
2 sen(2x). Hallar {x ∈ [0; 2π] / g (x) = 1}
66. Indicar cuál de las siguientes funciones pertenece a cada gráfica de la figura:
y = 2cos(t – π/2)
y = 2cos(t)
y = 2cos(t + π/2)
Página 14 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
67. Sea f (x) = -2cos (2x – π) + b. Determinar el valor de b para que Im (f) = [1; 5]. Con el valor
de b hallado, encontrar un x0 tal que f (x0) = 1 y un x1 tal que f (x1) = 5.
68. Resolver las siguientes ecuaciones trigonométricas:
a)
1 − sen 2 ( x) − sen( x). sec( x) = 1 +
1
cot g ( x)
 x
 x
2
2
2
1
sen (2 x
c) 1 −
=
2
4(cos(2 x) + sen ( x)) 2
en [0; 2π]
b) 2 1 − cos 2   . cos  + cos( x).tg ( x) = sen( x)


d) − 1 + 2 cos 2  x +
π
π
2
 = 1 − sen  x + 
2
2

en [-π; π]
en [π; 3π]
en [0;2π]
69. El péndulo de un reloj se mueve periódicamente, separándose s cm de la vertical. La
ecuación que describe el movimiento es
s (t) = 5sen(4πt).
Donde: s (t) representa la distancia de la pesa a la vertical.
a) Representar s (t).
b) Decidir a qué distancia de la vertical, y de qué lado de la misma, estará la pesa:
i) a los 4/3 seg.
ii) a los 2 seg.
iii) a los 17/8 seg.
c) ¿Qué distancia máxima alcanza?
d) ¿En qué instante alcanza la distancia máxima?
e) Indicar el período.
70. El proceso rítmico de la respiración consiste de períodos alternados de inhalación y
exhalación. Cada 4 seg se lleva a cabo un ciclo completo.
Si F representa el flujo de aire en el tiempo t (en 1/seg), y la máxima intensidad de flujo es 0,6
Página 15 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
1/seg, obtener una fórmula para F:
F (t) = a.sen(bt)
71. La tensión V de un toma corrientes en una casa está dada, como función del tiempo t (en
segundos), por V (t) = V0 cos(120πt).
a) ¿Cuál es el período de la oscilación?
b) ¿Qué representa Vv?
72. Las funciones trigonométricas de la forma y = a + b sen ω(t – t0) en donde a, b, ω y t0 son
constantes reales, se usan con frecuencia para simular la variación en la temperatura. Suponer
que F (t) = 60 + 10sen π/2(t – 8), con 0 ≤ t ≤ 24, da la temperatura Fahrenheit F a las t horas
después de la medianoche de cierto día.
a) ¿Cuál es la temperatura de las 8:00 am? ¿Y a las 12:00 del medio día?
b) ¿En qué momento F (t) = 60?
c) Encontrar las temperaturas máximas y mínimas y los tiempos en que se dan.
73. Si el voltaje dado por V = V0 sen (ωt + α) se imprime en un circuito en serie, se produce
una corriente alterna. Si V = 110 voltios, ω = 120π radianes por segundo, y α = -π/6, ¿cuándo
será el voltaje igual a cero?
74.La atenuación de un haz de fotones al atravesar un medio sigue una ley exponencial de la
 µ
forma N = N o exp −
 ρ

ρt  donde No es el número inicial de fotones; µ/ρ es el coeficiente de

atenuación expresado en [cm2/g]; ρ es la densidad del medio atravesado en [g/cm3] y t [cm], el
espesor de material requerido para disminuir el número de fotones incidentes al valor deseado.
a) Determine el espesor t [mm] de plomo y de concreto necesario para reducir el número
de fotones incidentes a la cuarta parte de su valor original.
b) Realice una gráfica de N (número de fotones) en función del espesor de material t.
Datos:
-Densidad del hormigón: 2,3 g/cm3.
-Coeficiente de atenuación del hormigón (E = 0,5 MeV): 8,915x10-3 m2/kg.
-Densidad del plomo: 11350 kg/m3.
-Coeficiente de atenuación del plomo (E = 0,5 MeV): 1,614x10-1.
75. Los constructores del oleoducto Trans-Alaska usaron forro aislante para evitar que el calor
del petróleo caliente del ducto derritiera el suelo permanentemente congelado debajo de él.
Para diseñar los forros fue necesario considerar la variación en la temperatura del aire a lo
largo del año. La siguiente figura muestra cómo se puede usar una función seno para
representar los datos de temperatura. Los puntos de la gráfica representan la temperatura
media del aire en Fairbanks, Alaska, con base en los registros del Servicio Nacional del Clima,
de 1941 a 1970. La función seno usada para ajustar los datos es:
 2π
(x − 101) + 25
f ( x ) = 37 sin 
 365

Página 16 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
donde f es la temperatura en grados Fahrenheit y x es el número del día contado desde el inicio
del año. Encuentrar:
i.
ii.
iii.
iv.
la amplitud;
el período,
el desplazamiento horizontal,
el desplazamiento vertical.
76. Aplicando las leyes de Kirchhoff se pueden determinar las corrientes I1, I2 e I3 de un circuito
como el de la figura.
Luego de usar la primera y segunda regla de Kirchhoff las relaciones establecidas son las
siguientes:
I1 + I2 = I3
10V – (6Ω)·I1 – (2 Ω)·I3 = 0
10 = (8 Ω )·I1 + (2 Ω)·I2
Encuentre los valores de I1, I2 e I3 por el método de sustitución o de igualación.
77.a- Para determinar la carga de un capacitor que se está cargando como función del tiempo,
se puede usar la siguiente expresión:
q(t) = Q[1 – exp(-t/RC)]
Determine la carga para t = 0, t → ∞. ¿Cuánto tiempo tarda el capacitor en llegar al 63% de la
carga máxima? Suponga Q = 60 µC, R = 800 kΩ, C = 5 µF. Grafique.
78.b- Para determinar la carga de un capacitor que se está descargando en función del tiempo,
Página 17 de 18
[UNRN – Sede Andina – Análisis Matemático I]
[2012]
se puede usar la siguiente expresión:
q(t) = Q·exp(-t/RC)
Determine la carga para t = 0, t → ∞. ¿Cuánto tiempo tarda el capacitor en llegar al 50% de su
carga máxima? Suponga Q = 60 µC, R = 800 kΩ, C = 5 µF. Grafique.
79. Si suponemos una eficiencia de colección de fotoelectrones casi total, la ganancia de un
tubo fotomultiplicador se puede obtener aplicando la siguiente relación:
G = αδN
donde:
G = ganancia del tubo fotomultiplicador.
α=1
δ = factor de multiplicación
N = número de etapas.
a) ¿Cuántas etapas se necesitan para obtener una ganancia de 1010?
b) ¿Qué ganancia se obtendría con 5 etapas?
Realice un gráfico semilogarítmico para representar la ganancia G en función del número N de
etapas.
80. La figura muestra un circuito que consta de un resistor, un inductor y un capacitor
conectados en serie a través de una fuente AC de voltaje. Se supone que el voltaje varía
senoidalmente con el tiempo, es decir, v = Vmsin(ωt). Analizando el circuito, se establece que la
caída instantánea de voltaje de los tres elementos puede expresarse como:
vR(t) = VR·sin(ωt)
vL(t) = VL· cos(ωt)
vC(t) = -VC·cos(ωt)
a) Grafique las funciones trigonométricas anteriores y analice qué ocurre con el
desplazamiento horizontal o desfasaje entre ellas.
Página 18 de 18