Plan Nuevo Segundo Parcial 2001 (Brea)
Anuncio
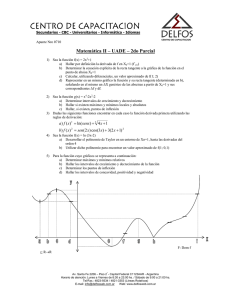
Secundarios - CBC - Universitarios - Informática - Idiomas CENTRO DE CAPACITACION Apunte Nº 184 UADE - Matemática I (Plan Nuevo) – Cát. Brea – Año 2001 – Modelo 2º parcial 1- Hallar la ecuación de la recta tangente a la función extremo de la misma. F ( x) = − x + 4. x + 1 en un 2- Desarrollar según un polinomio de Taylor de orden 2 en Xo=1 3- Derivar [ F ( x) = ] F ( x) = cos 3 (ln x ) + 2 x − 2 1 1 − 2.x 4- Dado el gráfico de F(x), hallar: dominio, imagen, raíces, intervalos de crecimiento y decrecimiento, intervalos de concavidad positiva y negativa, máximos y mínimos (absolutos y relativos, puntos de inflexión y asíntotas. 3 1 -10 -8 -7 -3 -3 -6 2 5- Dada F(x)= -1/2.x +2.x+3/2 en Xo=1 a) Hallar el diferencial. b) Calcular en forma aproximada el valor de F(0,5) c) Trazar la recta tangente por el punto X0=1, y hallar ∆x ; dF e incremento sobre la grafica. 6- Determinar intervalos de crecimiento y concavidad de F(x), siendo Desarrollar por Taylor hasta orden máximo en X0=2. F ( x) = ( F ' ( x) = ) 5 x + 2 + x2 Av. Santa Fe 2206 – Piso 2º - Capital Federal C1123AAR - Argentina Horario de atención: Lunes a Viernes de 8:30 a 23:00 hs. / Sábado de 9:00 a 21:00 hs. Tel/Fax.: 4823-9334 / 4821-3353 (Líneas Rotativas) Web: www.delfosweb.com.ar E-mail: [email protected] x +1 x2 +1





![[a=b o a.b = 2]. Decidir si es equivalencia.... Ù R](http://s2.studylib.es/store/data/001072818_1-5e24d2625d4b0c34ccd187502a7e8112-300x300.png)




