17. DOMINIO FRECUENCIA – CRITERIO DE BODE

327
17. DOMINIO FRECUENCIA – CRITERIO DE BODE
17.1 INTRODUCCION
Las técnicas para analizar la respuesta de un sistema en el dominio de la frecuencia
son las más populares para el análisis y diseño del control de sistemas lineales. Se
fundamentan en que cuando un sistema es perturbado con una entrada sinusoidal, la
respuesta del sistema alcanza una estabilidad también sinusoidal con igual
frecuencia pero diferente amplitud y existiendo una fase entre ellas. A continuación
se introducen algunos conceptos derivados de la respuesta seno de un sistema lineal
de primer orden y posteriormente se generalizan a otras dinámicas
Respuesta sinusoidal de un sistema de primer orden
Si la variable de entrada de un sistema con atraso de primer orden es perturbada con
un cambio sinusoidal de la forma
x (t ) = X o sin wt
(17.1)
La respuesta del sistema en el dominio del tiempo corresponde a la siguiente
expresión
Y (t ) =
Siendo
KX o wτ −t / τ
KX o
e
+
sin(wt + θ )
2 2
1 + w 2τ 2
1+ w τ
θ = tan −1 (− wτ ) = − tan −1 ( wτ )
(17.2)
(17.3)
Para un sistema de primer orden con ganancia 5 y constante de tiempo uno, con
perturbación sinusoidal en la variable de entrada de amplitud 3 y frecuencia igual a 2
rad/sec se obtiene una respuesta como la que se observa en la Figura 17.1.
Después de un tiempo la contribución a la respuesta del término exponencial se
anula y la respuesta se mantiene en una estabilidad oscilatoria de tipo sinusoidal
correspondiente al segundo término de la ecuación (17.2), es decir,
328
Figura 17.1. Respuesta Seno de un sistema de primer orden
Y ( t ) t muy
grande
=
KX
sin( wt + θ )
o
1 + w 2τ
2
(17.4)
La amplitud de esta señal de salida corresponde a la expresión factor del término
sinusoidal, es decir,
Yo =
KX
o
1 + w 2τ
2
(17.5)
La “Relación entre las amplitudes” o AR, entre las señales de salida y entrada es un
factor de la amplitud de la señal de entrada que permite calcular la amplitud de la
señal de salida. Para un sistema de primer orden, la relación de amplitudes se
expresa como
AR =
Mach
Yo
K
=
Xo
1 + w 2τ 2
(17.6)
329
La “Relación de magnitudes” o MR es la relación entre las amplitudes dividida por
la ganancia en estado estacionario, es decir,
MR =
AR
K
(17.7)
El “Angulo fase” es la cantidad de radianes o grados de atraso o adelanto de la señal
de salida con respecto a la señal de entrada. Cuando el ángulo fase es positivo
expresa un adelanto mientras que cuando es negativo corresponde a un atraso. El
ángulo fase se calcula con la ecuación (17.3)
Las ecuaciones (17.3), (17.6) y (17.7) muestran que los tres términos, AR, MR y θ,
son funciones de la frecuencia de la señal de entrada y dependen de la dinámica del
sistema
17.2 DINAMICA DE UN SISTEMA - DOMINIO FRECUENCIA
El análisis dinámico de un sistema en el dominio de la frecuencia consiste
esencialmente en el estudio de la variación del AR o MR y θ con el cambio en la
frecuencia en la señal de entrada
Mediante la evaluación de la función de transferencia de un sistema para s = jw , se
pueden demostrar las siguientes ecuaciones para AR y θ.
Yo
= G ( jw )
Xo
θ = ∠ G ( jw )
AR =
(17.8)
(17.9)
Siendo G ( jw) , la expresión compleja que resulta al evaluar la función de
transferencia del sistema para s = jw y que se denomina la Función de
Transferencia Sinusoidal del sistema. Las ecuaciones (17.8) y (17.9) expresan que la
magnitud de la función de transferencia sinusoidal es igual al AR y su argumento es
igual a θ
La Tabla 17.1 muestra, para algunas dinámicas de sistemas su función de
transferencia y las ecuaciones que calculan sus respectivas razones de amplitudes y
ángulos fase
Mach
330
Tabla 17.1 Relación de Amplitudes y Fase para Sistemas
Sistema
Ganancia Pura
Atraso de Primer Orden
G (s )
AR
θ
K
1
0
K
τs + 1
K
1+ w τ
2
tan −1 (− wτ )
2
Atraso de Segundo Orden
K
τ s + 2τζ s + 1
(1 − w 2τ 2 ) 2 + ( 2τζ w ) 2
 2τζ w 
− tan 
2 2 
1 − w τ 
Adelanto de Primer Orden
K (1 + τ s )
K 1 + w2τ 2
θ = tan(wτ )
e−to s
1
θ = −t o w
1
w
θ =−
Sistema Tiempo Muerto
Sistema Integrador
Controlador PI
Controlador PID
2
2
K
1
s
 τ s +1

Kc  I
 τIs 
 τ Iτ D s 2 + τ I s + 1 

Kc 
τ
s
I


Kc 1 +
Kc
2
 −1
tan −1 
 wτ I
1
(τ I w) 2

1 

1 + τ D w −
τ I w 

π
2

 < 0


1 

tan −1  τ D w −
w τ I 

331
Algunas anotaciones sobre los diferentes sistemas son:
Sistema de segundo orden: La respuesta de un sistema de segundo orden en el
dominio de la frecuencia depende de la constante de tiempo y del factor de
amortiguamiento del sistema, además de la frecuencia de la función sinusoidal de
entrada
Sistema adelanto de primer orden: Para este sistema, el signo de la ecuación para
la fase confirma el adelanto del sistema y la ecuación para la relación de amplitudes
explica el por qué no pueden existir sistemas de solo adelantos puros. Se deduce de
dicha ecuación que la relación de amplitudes aumenta con la frecuencia de la señal
de entrada lo que significa que un ruido de alta frecuencia, que está siempre presente
en las señales naturales, sería amplificado infinitamente
Sistema de tiempo muerto puro: Para este sistema, es importante observar que la
fase aumenta negativamente con el aumento en la frecuencia. La rapidez de
disminución de θ depende de to, a mayor tiempo muerto mas rápido disminuye la
fase. Este hecho es importante en el análisis de sistemas de control. La relación entre
las amplitudes y la relación de magnitudes son independientes de la frecuencia
cuando la función de transferencia es un tiempo muerto puro.
Sistema integrador: En un sistema integrador, la relación entre las amplitudes es
inversamente proporcional a la frecuencia mientras que el ángulo fase se mantiene
constante a -90°. Es decir, el integrador suministra un atraso de fase constante
Controlador PID: En este sistema, el valor de θ puede ser positivo (adelanto de
fase) o negativo (atraso de fase) dependiendo de los valores τD, τI y w
Ecuaciones generales para el AR y el θ de un sistema
Para un sistema con función de transferencia OLTF de la forma
m
OLTF =
K ∏ (τ i s + 1)e −to s
i =1
s
k
∏ (τ
n
j s + 1)
,
(n + k) > m
i =1
Las ecuaciones para AR y θ son las siguientes,
(17.10)
332
m
AR =
K ∏ (τ i w) + 1
i =1
n
2
wk ∏ (τ j w) + 1
2
(17.11)
i=1
θ = ∑tan−1 (τ i w) − to w − ∑tan−1 ((τ j w) − k(π )
m
n
i=1
j =1
(17.12)
El análisis dinámico de sistemas en el dominio de la frecuencia se realiza valiéndose
de las características que se derivan de las variaciones de sus relaciones de
amplitudes y fases con el cambio en la frecuencia. Son varios los recursos o criterios
establecidos y entre ellos encontramos el de Bode, Nyquist y Nichols. A
continuación se explican los denominados Diagramas de Bode para los sistemas
incluidos en la Tabla 17.1 y seguidamente el Criterio de Bode que define la
estabilidad de un sistema.
17.3 DIAGRAMAS DE BODE
Los diagramas de Bode son gráficos de AR o MR y θ en función de la frecuencia.
Una representación de Bode consiste de dos gráficos: (1) log AR (o log MR) vs. Log
w y (2) θ vs. Log w. Frecuentemente, el término 20 Log AR se expresa en decibeles
y se grafica en vez de Log AR
Gráficos de Bode de un elemento de ganancia pura
Los gráficos de Bode correspondientes a un elemento de ganancia pura se observan
en la Figura 17.2. El valor de AR es constante e igual al valor de la ganancia y el
ángulo fase es constante e igual a 0°
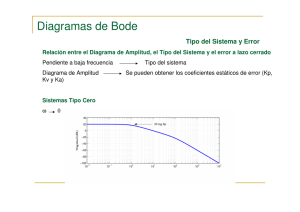
Gráficos de Bode de un sistema con atraso de primer orden
Los gráficos de Bode correspondientes a un sistema con atraso de primer orden se
observan en la Figura 17.3. El gráfico de AR vs w se caracteriza por mostrar una
asíntota de baja frecuencia de pendiente cero y una asíntota de alta frecuencia de
pendiente menos uno. La frecuencia de esquina, es decir la intersección entre las dos
asíntotas se localiza en 1/ τ . En el gráfico del ángulo fase se nota que a bajas
Mach
333
frecuencias la fase es 0°, mientras que a altas frecuencias se aproxima a -90°. En la
frecuencia de esquina, el ángulo fase es de -45°.
Figura 17.2. Gráficos de Bode para un sistema de Ganancia Pura
( ( K = 10)
Figura 17.3. Gráficos de Bode de un sistema con atraso de primer orden
( K = 5, τ = 1)
Mach
334
Gráficos de Bode de un sistema de segundo orden
Los gráficos de Bode para un sistema de segundo orden dependen del valor del
factor de amortiguamiento y se observan en la Figura 17.4. En el gráfico de AR se
nota una asíntota de baja frecuencia de pendiente cero y una asíntota de alta
frecuencia de pendiente -2. La frecuencia de esquina se localiza en 1/ τ . La
transición del AR desde baja a alta frecuencia depende del valor de ζ . A bajas
frecuencias el ángulo fase se aproxima a 0°, mientras que a altas frecuencias se
aproxima a -180°. En la frecuencia de esquina, el ángulo fase es de -90°.
Figura 17.4. Gráficos de Bode para un sistema de segundo orden
( K = 1, τ = 1)
Gráficos de Bode de un sistema adelanto de primer orden
Los gráficos de Bode correspondientes a un sistema adelanto de primer orden se
observan en la Figura 17.5. El gráfico de AR vs w se caracteriza por mostrar una
asíntota de baja frecuencia de pendiente cero y una asíntota de alta frecuencia de
pendiente +1. En el gráfico del ángulo fase se nota que a bajas frecuencias la fase es
0°, mientras que a altas frecuencias se aproxima a +90°. En la frecuencia de esquina,
Mach
335
el ángulo fase es de +45°. Por lo tanto, un sistema con adelanto de primer orden
proporciona un adelanto de fase.
Figura 17.5. Diagramas de Bode de un sistema con adelanto de primer orden
( K = 5, τ = 1)
Gráficos de Bode de un sistema de tiempo muerto puro
Los gráficos de Bode correspondientes a un sistema de tiempo muerto puro se
observan en la Figura 17.6. Cuando la frecuencia aumenta, el ángulo fase se hace
más negativo. Entre mayor es el valor del tiempo muerto, mas rápido disminuye el
ángulo fase (se vuelve mas rápidamente negativo) sin límite
Gráficos de Bode de un sistema integrador
Los gráficos de Bode correspondientes a un sistema integrador se observan en la
Figura 17.7. Se observa un gráfico de AR o MR que es una línea recta con pendiente
-1 y se cumple que a una frecuencia de 1 radian/unidad de tiempo, la AR o MR es
igual a uno
Mach
336
Figura 17.6. Diagramas de Bode de un sistema de tiempo muerto puro
(t o = 0.1)
Figura 17.7. Gráficos de Bode para un sistema integrador
( K = 1, τ = 1)
Mach
337
Gráfico de Bode de un controlador PI
Los gráficos de Bode correspondientes a un controlador proporcional integral se
observan en la Figura 17.8. Se nota un gráfico de AR o MR que es una línea recta
con pendiente El gráfico de AR versus w, para un controlador PI, se caracteriza por
mostrar una asíntota de baja frecuencia de pendiente -1 y una asíntota de alta
frecuencia de pendiente cero en el valor de AR/Kc = 1.0. La frecuencia de esquina,
es decir la intersección entre las dos asíntotas se localiza en wτ I . En el gráfico del
ángulo fase se nota que a bajas frecuencias la fase es -90°, mientras que a altas
frecuencias se aproxima a 0°. En la frecuencia de esquina, el ángulo fase es de -45°.
Figura 17.8. Diagrama de Bode – Controlador PI
( K = 5,τ = 2)
Gráfico de Bode de un controlador PID
Los gráficos de Bode correspondientes a un controlador proporcional integral
derivativo se observan en la Figura 17.9. El gráfico de AR versus w, muestra una
asíntota de baja frecuencia de pendiente -1, otra de alta frecuencia de pendiente 1 y
otra entre las dos de pendiente cero para una ordenada de AR/Kc igual a uno. . Se
observan dos frecuencias de esquina localizadas en 1/τI y en 1/τD
Mach
338
Figura 17.9. Diagrama de Bode – Controlador PID
( K = 5,τ I = 10,τ D = 2)
Gráficos de Bode de sistemas complejos
Las ecuaciones (17.11) y (17.12) permiten la construcción de los gráficos de Bode
para sistemas complejos con funciones de transferencia que incluyen tiempo muerto,
además de zeros y polos como la siguiente:
G(s) =
10(s + 1)e − s
s(2s + 1)(3s + 1)
Los comandos disponibles en Matlab permiten la construcción del diagrama de
Bode con mucha facilidad y que se muestra en la Figura 17.10. A bajas frecuencias,
w < 0.33, la pendiente es -1 a causa del término integrador. A una frecuencia w =
0.33, uno de los atrasos de primer orden comienza a contribuir al gráfico y, por lo
tanto, la pendiente de la gráfica cambia a -2 a esta frecuencia. A una frecuencia w =
0.5, el otro atraso de primer orden comienza a contribuir cambiando la pendiente de
la asíntota a -3. Finalmente, a una frecuencia w = 1, el adelanto de primer orden
entra con una pendiente de +1 y la pendiente de la asíntota cambia nuevamente a -2.
Mach
339
En forma similar, el gráfico del ángulo fase se obtiene mediante la suma algebraica
de los ángulos individuales.
Figura 17.10. Gráficos de Bode para un sistema complejo
17.4 DIAGRAMAS DE BODE – CONSTRUCCION CON MATLAB
Matlab dispone del comando “bode” para calcular las magnitudes y los ángulos de
fase de la respuesta de un sistema en el dominio de la frecuencia en tiempo continuo,
lineal e invariante con el tiempo. Cuando se introduce el comando sin argumentos en
el lado izquierdo, se producen las representaciones de Bode en la pantalla definiendo
el numerador y el denominador de la función de transferencia ya sea previamente o
directamente como argumentos, es decir en la forma de
bode(num, den)
Si se define la función de transferencia en el sistema LTI con un nombre, por
ejemplo, sys, entonces el comando ”bode” solo incluye como argumento el nombre
de la función de transferencia, es decir
Mach
340
bode(sys)
En forma similar a lo anterior, también se puede introducir la función de
transferencia en el sistema LTI directamente como argumento del comando.
Con el comando “bode” se representan repuestas de varios sistemas LTI sobre una
misma figura. Todos los sistemas deben tener el mismo número de entradas y
salidas. La sintaxis es de la forma
bode(sys1, sys2,…, sysN)
Se pueden especificar los estilos de las representaciones para cada uno de los
sistemas con la siguiente sintaxis
bode(sys1,’PlotStyle’,…, sysN, ‘PlotStyleN’)
Cuando se invoca el comando “bode” con argumentos en el lado izquierdo en la
forma
[mag, fase, w] = bode(sys, w)
Matlab retorna la respuesta del sistema en el dominio de la frecuencia en las
matrices mag, fase y w. No aparece una gráfica en la pantalla. Las matrices mag y
fase contienen las magnitudes y los ángulos de fase de respuesta del sistema en el
dominio de la frecuencia evaluado en los puntos de frecuencia especificados por el
usuario, w = {wmin, wmax}. El ángulo de fase se retorna en grados. La magnitud se
convierte en decibeles con el enunciado
magdb = 20 Log10(mag)
17.5. CASOS DE ESTUDIO
Construya los diagramas de Bode para las siguientes funciones de transferencia
Mach
341
a. G ( s ) =
b. G ( s ) =
K
( s + 1)(2 s + 1)(10 s + 1)
K ( 3 s + 1)
( s + 1) (2 s + 1)(10 s + 1)
Ke − s
c. G ( s ) =
( s + 1) (2 s + 1 )(10 s + 1)
K ( 3 s + 1) e − s
d. G ( s ) =
( s + 1) (2 s + 1)(10 s + 1)
17.6 CRITERIO DE ESTABILIDAD DE BODE
El criterio de estabilidad de Bode para la respuesta de un sistema en el dominio de la
frecuencia, puede determinar los límites de estabilidad para lazos de control por
retroalimentación aún cuando se incluya un tiempo muerto en el lazo. El criterio
consiste en determinar la frecuencia a la cual el ángulo fase de la función de
transferencia de lazo abierto es -180° (-π radianes) y la Relación entre las
Amplitudes para dicha frecuencia. El criterio de estabilidad de Bode determinado
sobre la base de la respuesta de un sistema en el dominio de la frecuencia se puede
establecer de la siguiente manera:
Para que un sistema sea estable, la Relación entre las Amplitudes debe ser menor
que la unidad cuando el ángulo fase es -180° (-π radianes). Es decir,
Si AR < 1 a un θ = - 180°, el sistema es estable
Si AR > 1 a un θ = - 180°, el sistema es inestable
Para un AR = 1 a un θ = - 180°, los diagramas de Bode de una lazo de control por
retroalimentación permiten determinar la ganancia última del controlador, Kcu. La
frecuencia a la que se alcanza esta condición es la frecuencia última, ωn. El período
último se puede calcular a partir de esta frecuencia, mediante la fórmula Tu = 2π/ωn
Mach
342
Análisis de estabilidad de un lazo de control proporcional mediante el
Diagrama de Bode
Considere un lazo de control con las siguientes funciones de transferencia para cada
uno de sus elementos.
Controlador:
Gc ( s) = K c
Válvula de control:
Gc ( s ) =
0.016
3s + 1
(17.14)
Proceso:
Gc ( s ) =
50
30 s + 1
(17.15)
Sensor/Transmisor:
Gc ( s ) =
1
10s + 1
(17.16)
(17.13)
La función de transferencia en lazo abierto (OLTF) es por lo tanto:
OLTF =
0 .8 K c
(10 s + 1)(30 s + 1)(3s + 1)
(17.17)
El diagrama de bode correspondiente a la función de transferencia de lazo abierto
(17.17) se muestra en la Figura 17.11
Construya el diagrama de bode de la Figura 17.11 y haga un clic izquierdo en la
intersección de la gráfica inferior con la línea correspondiente a una fase de -180°
y en el cuadro desplegado observe la correspondiente frecuencia. A continuación
haga un clic izquierdo sobre el gráfico superior para determinar la magnitud o
Relación de magnitudes a la frecuencia obtenida anteriormente. Observe los valores
encontrados en la Figura 17.11
¿Cuánto es el valor de la ganancia última? _________________________________
¿Cuánto es el valor del período último? ___________________________________
Mach
343
Figura 17.11. Diagrama de bode para el lazo de control proporcional
Para observar la respuesta paso unitario del lazo cerrado de control con diferentes
valores asignados a la ganancia del controlador, construya el siguiente archivo con
nombre bodeultimo.m
% Respuesta paso unitario de un lazo cerrado de control
Kc = input('Ganancia del controlador, Kc = ');
% Funciones de Transferencia
hc = Kc;
% Controlador
hv = tf([0.016],[3 1]);
% Válvula de Control
hp = tf([50],[30 1]);
% Proceso
ht = tf([1],[10 1]);
% Sensor/Transmisor
h1 = hc*hv*hp;
% Serie controlador – válvula - proceso
hf = feedback(h1,ht);
% Lazo de retroalimentación negativo
step(hf)
% Respuesta paso unitario
Ejecute el archivo asignando un valor para la ganancia del controlador igual al
determinado como ganancia última. Observe la inestabilidad de la respuesta.
Repita la observación anterior, ejecutando el archivo para ganancias menores que
la última. ¿Qué observa en la respuesta obtenida para una ganancia con un valor
Mach
344
de la mitad del valor último?. La respuesta obtenida para una ganancia de 11.9 se
observa en la Figura 17.12
Figura 17.12. Respuesta paso unitario para el lazo cerrado de control proporcional
Análisis del efecto del tiempo muerto en la estabilidad de un lazo de
control proporcional mediante el Diagrama de Bode
Agréguele un tiempo muerto de 2 segundos al lazo de control con la OLTF de la
ecuación (17.17) y construya el diagrama de Bode correspondiente como se
muestra en la Figura 17.13
¿Cuánto es el valor de la nueva ganancia última? ____________________________
¿Cuánto es el valor del nuevo período último? ______________________________
¿Qué significan estas disminuciones con respecto a la inestabilidad del proceso y la
rapidez de la respuesta del lazo cerrado?
Mach
345
Figura 17.13. Diagrama de Bode para lazo de control proporcional con tiempo
muerto
Análisis del efecto de la acción integral en la estabilidad de un lazo de
control proporcional – integral mediante el Diagrama de Bode
Considere que el controlador del lazo considerado en la OLTF de la ecuación
(17.17) es de acciones proporcional e integral y no incluye tiempo muerto. La Figura
17.14 muestra el diagrama de Bode para un controlador proporcional – integral con
un tiempo integral de 1 segundo
Construya el diagrama de bode de la Figura 17.14 (Tiempo integral = 1 segundo) y
determine la frecuencia y la relación de magnitudes para una fase de -180°.
¿Cuánto es el valor de la nueva ganancia última? ____________________________
¿Cuánto es el valor del nuevo período último? ______________________________
¿Qué significan estas disminuciones con respecto a la inestabilidad del proceso y la
rapidez de la respuesta del lazo cerrado con controlador proporcional?
Mach
346
Sobre la misma Figura 17.14, construya otro diagrama de Bode cambiando el
tiempo integral a 10 segundos.
¿Qué efecto se observa al aumentar considerablemente el tiempo integral?
Figura 17.14. Diagrama de Bode para el lazo de control proporcional – integral
Análisis del efecto de la acción derivativa en la estabilidad de un lazo de
control proporcional – derivativo mediante el Diagrama de Bode
Considere que el controlador del lazo considerado en la OLTF de la ecuación
(17.17) es de acciones proporcional – derivativa y no incluye tiempo muerto. La
Figura 17.15 muestra el diagrama de Bode para un controlador proporcional –
derivado con un tiempo derivativo de 15 segundos y una función de transferencia
dada por la siguiente expresión:
 1 + 15s 
Gc (s) = K c 

 1 + 1.5s 
Mach
(17.18)
347
Figura 17.15. Diagrama de Bode para el lazo de control proporcional – derivativo
Construya el diagrama de bode de la Figura 17.15 y determine la frecuencia y la
relación de magnitudes para una fase de -180°.
¿Cuánto es el valor de la nueva ganancia última? ____________________________
¿Cuánto es el valor del nuevo período último? ______________________________
¿Qué significan estos aumentos con respecto a la inestabilidad del proceso y la
rapidez de la respuesta del lazo cerrado con controlador proporcional?
17.7 DESEMPEÑO DE UN CONTROLADOR – CRITERIO DE BODE
La respuesta de un sistema en el dominio de la frecuencia constituye un
procedimiento para obtener la ganancia última y la frecuencia última de un lazo de
control. Después de estimadas estas dos especificaciones se pueden aplicar las
ecuaciones de Ziegler-Nichols para ajustar los parámetros de acción del controlador.
Las técnicas basadas en la respuesta en el dominio de la frecuencia incluyen otras
Mach
348
tres especificaciones para la sintonización de controladores como son: el margen de
ganancia, el margen de fase y la respuesta en lazo cerrado.
Respuesta en Lazo Abierto
El margen de ganancia y el margen de fase se basan en la respuesta en el dominio de
la frecuencia de la función de transferencia de lazo abierto, mientras que la respuesta
en lazo cerrado se basa en la respuesta en el dominio de la frecuencia de la función
de transferencia del lazo cerrado
Margen de ganancia
El margen de ganancia, GM, es una especificación típica del desempeño de un
controlador asociada con la técnica en el dominio de la frecuencia. El margen de
ganancia representa el factor mediante el cual la ganancia total del lazo debe
aumentarse para hacer que el sistema se vuelva inestable. La ganancia del
controlador que produce un margen de ganancia determinado se calcula de la
siguiente manera:
Kc =
K cu
K cu
=
GM
K ( GM ) MR |θ = − 180 °
(17.19)
Siendo K, el producto de las ganancias de todos los otros elementos en el lazo. Una
especificación típica es que GM ≥ 2 . Obsérvese que la sintonización de un
controlador proporcional con GM = 2 es la misma regla de sintonización de ZieglerNichols para una razón de decaimiento de un cuarto
Margen de fase
El margen de fase, PM, es otra especificación comúnmente asociada con el
procedimiento de la respuesta de un sistema en el dominio de la frecuencia. El
margen de fase es la diferencia entre – 180° y el ángulo fase a la frecuencia a la cual
la Relación entre las amplitudes, AR, es uno. Es decir,
PM = 180 + θ | AR=1
Mach
(17.20)
349
PM representa la cantidad adicional requerida de atraso de fase para hacer que el
sistema sea inestable. Una especificación típica es PM > 45°.
Determinación de Margen de Ganancia y de Fase: Matlab
El comando “margin” calcula el margen de ganancia (Gm), el margen de fase (Pm)
y las correspondientes frecuencias de cruce (Wcg, Wcp) de sistemas SISO en lazo
abierto.
Cuando se introduce el comando “margin” a la computadora (sin argumentos en el
lado izquierdo), Matlab produce las representaciones de Bode con los márgenes de
ganancia y de fase marcados con lineas verticales. Los argumentos requeridos para
el comando “margin” son el numerador y denominador de la función de
transferencia, es decir en la forma de
margin(num, den)
Si se define la función de transferencia en el sistema LTI con un nombre, por
ejemplo, sys, entonces el comando ”margin” solo incluye como argumento el
nombre de la función de transferencia, es decir
margin(sys)
Cuando se invoca el comando “margin” con argumentos en el lado izquierdo en la
forma
[Gm, Pm. Wcg, Wcp] = margin (sys)
Matlab calcula el margen de ganancia, el margen de fase y las correspondientes
frecuencias de cruce para el sistema SISO de nombre “sys” de lazo abierto.
La Figura 17.16 muestra el Diagrama de Bode para la función de transferencia de
lazo abierto correspondiente a la ecuación (17.17), para un controlador proporcional
con una ganancia de 10
Mach
350
Utilice el comando “margin” para la función de transferencia de la ecuación
(17.17) con ganancia de 10 y verifique los valores que se observan en la Figura
17.16 para el margen de ganancia, el margen de fase y las correspondientes
frecuencias de cruce
Utilice las funciones de transferencia utilizadas anteriormente para los
controladores proporcional – integral y proporcional – integral – derivativo,
asígneles ganancias menores que la última y determine los valores correspondientes
a sus márgenes de ganancia, márgenes de fase y frecuencias de cruce. Trate de
conseguir, en lo posible, los valores recomendados para los márgenes de ganancia
y de fase
Figura 17.16. Diagrama de Bode con márgenes de ganancia y de fase y frecuencias
de cruce
Respuesta en lazo cerrado
La respuesta en lazo cerrado, CLR, es otra especificación del desempeño de un
controlador asociada con las técnicas de la respuesta en el dominio de la frecuencia
y se basa en la función de transferencia de lazo cerrado.
Mach
351
Considere la siguiente función de transferencia de lazo cerrado con respecto al valor
deseado de la variable de proceso
0 .8 K c
T (s)
=
set
3
2
T ( s ) 900 s + 420 s + 43 s + (1 + 0 .8 K c )
(17.21)
El diagrama de Bode correspondiente a la función de transferencia (17.21) para
diferentes valores de Kc se muestra en la Figura 17.17.
Figura 17.17. Diagrama de Bode de la función de transferencia de lazo cerrado
(17.21)
Lo más significativo que muestra la figura es que cuando Kc aumenta la frecuencia
de esquina se desplaza a la derecha y también aumenta la altura del pico. Al igual
que para la función de transferencia de lazo abierto, la frecuencia de esquina para la
función de transferencia de lazo cerrado, ω cCL , es el inverso de la constante de
tiempo del lazo cerrado, τ CL . Por lo tanto, el desplazamiento a la derecha de ω cCL es
Mach
352
deseable porque a mayor valor de ω cCL menor es el valor del τ CL y, en consecuencia,
más rápida es la respuesta del proceso en lazo cerrado
Sin embargo, cuando Kc aumenta, la altura del pico también aumenta. Este pico,
denominado Pico de Resonancia, se relaciona con la razón de amortiguamiento del
lazo cerrado, ζ CL . Entre mayor es el pico mas pequeño es la razón de
amortiguamiento y, por consiguiente, mas subamortiguada (oscilatoria) es la
respuesta en lazo cerrado. Esta razón de amortiguamiento es equivalente a la razón
de amortiguamiento de lazo abierto de un sistema de segundo orden. Por lo tanto,
cuando Kc aumenta, resultan dos efectos conflictivos porque el proceso controlado
es más rápido pero más oscilatorio
Una especificación común para CLR es la de sintonizar el controlador para obtener
una Altura de pico máxima, MPH, de 1.26, que corresponde a una razón de
amortiguamiento, ζ CL de aproximadamente 0.4
Determinación del Pico y Frecuencia de Resonancia: Matlab
El pico de resonancia es el valor máximo de la magnitud (en decibeles) de la
respuesta en frecuencia en lazo cerrado. La frecuencia de resonancia es la frecuencia
a la cual se encuentra la máxima magnitud. Las órdenes de Matlab que se pueden
utilizar para obtener el pico de resonancia y la frecuencia de resonancia se muestran
en el siguiente archivo de nombre picoderesonancia.m. Mediante este archivo se
contruye el Diagrama de Bode para el sistema en lazo cerrado con una ganancia con
un valor de 15 para el controlador:
% Pico de resonancia y Frecuencia resonante
w = logspace(-1,1);
h = tf([12],[900 420 43 13]);
bode(h,w)
[mag,phase,w] = bode(h,w);
frecuencia
[Mp,k] = max(mag);
pico_resonante = Mp
frecuencia_resonante = w(k)
% Limites del eje de las frecuencias
% Función de transferencia
% Diagrama de Bode
% Datos de la respuesta en
% Magnitud máxima
% Pico resonante
% Frecuencia resonante
Al ejecutar el archivo en la ventana de Matlab se observan las siguientes respuestas:
Mach
353
pico_resonante =
4.4917e+000
frecuencia_resonante =
1.7575e-001
Los anteriores resultados se pueden verificar en el diagrama de bode obtenido con el
mismo archivo y que se observa en la Figura 17.18
Figura 17.18. Diagrama de Bode en lazo cerrado
17.8
CASOS DE ESTUDIO
1. Construya el Diagrama de Bode para la siguiente función de transferencia en
lazo abierto
G (s) =
Mach
25
s ( s + 1)( s + 10)
354
Determine el margen de fase y el margen de ganancia
2. Construya el Diagrama de Bode para la siguiente función de transferencia en
lazo abierto
G (s) =
20( s + 1)
s ( s + 2 s + 10)( s + 5)
2
Determine el margen de fase y el margen de ganancia
Mach