05-analisis de respuesta frecuencial 1

7(0$$QiOLVLVGHODUHVSXHVWD
HQIUHFXHQFLD
1.
2.
3.
4.
Fases de diseño del controlador
Respuesta en frecuencia
Representación de la respuesta en frecuencia
Análisis de estabilidad en el dominio de la
frecuencia
5. Especificaciones de comportamiento en el dominio
de la frecuencia
“Ingeniería de control moderna”, K. Ogata, Prentice Hall, 5ª Ed., 2008. Cap. 8-9.
“Sistemas de control moderno”, R.C. Dorf y R.H. Bishop,Prentice Hall, 10ª Ed., 2005.
Cap. 8-9.
Tema 5: Análisis de respuesta en frecuencia
1
)DVHVGHGLVHxRGHOFRQWURODGRU
Determinar especificaciones de la planta
(establecer: objetivos, variables a controlar y especificaciones)
Modelado de la planta
(crear un modelo matemático de la planta)
Diseño del controlador
(analizar el modelo matemático de la planta y sintetizar un controlador)
Simulación del sistema dinámico
(validación del controlador en el modelo de la planta)
Implantación del controlador
(validación del controlador en la planta real)
Tema 5: Análisis de respuesta en frecuencia
2
5HVSXHVWDHQIUHFXHQFLDL
z
z
z
El término respuesta en frecuencia hace referencia a la respuesta (salida)
de un sistema a entradas sinusoidales cuya frecuencia se varía en un cierto
rango.
La respuesta de un sistema lineal a una entrada sinusoidal es:
•
una señal sinusoidal de la misma frecuencia que la entrada.
•
la magnitud y la fase de la señal de salida difieren de las de la señal de entrada,
siendo dicha diferencia función de la frecuencia de entrada.
La respuesta en frecuencia puede expresarse como la diferencia en
magnitud y fase entre las sinusoides de entrada y salida del sistema.
Tema 5: Análisis de respuesta en frecuencia
3
5HVSXHVWDHQIUHFXHQFLDLL
z
La función de transferencia de un sistema G(s) en el dominio de la
frecuencia, se expresa como:
u
z
G(s)
y
Y (s )
= G(s ) = G( jω) = M ( ω) ⋅ e j ⋅φ( ω ) = M ∠φ
U (s )
•
M (magnitud), expresa el cociente de amplitud de las señales sinusoidales de
salida y entrada en función de la frecuencia ω.
•
φ (fase), expresa el desplazamiento de fase entre ambas señales en función de la
frecuencia ω.
Sistema de fase mínima, aquel que tiene todos los ceros y polos de su
función de transferencia en el semiplano izquierdo del plano s.
Tema 5: Análisis de respuesta en frecuencia
4
5HVSXHVWDHQIUHFXHQFLDLLL
z
z
La magnitud M y la fase φ de un sistema dependen de los valores de los polos,
ceros y de la ganancia del sistema.
La respuesta en frecuencia de un sistema puede utilizarse para:
•
•
•
Localizar los polos y ceros del sistema.
Predecir el comportamiento del sistema en lazo cerrado.
Diseñar un controlador que mejore ciertas regiones de la respuesta en
frecuencia del sistema.
Tema 5: Análisis de respuesta en frecuencia
5
5HSUHVHQWDFLyQGHODUHVSXHVWDHQ
IUHFXHQFLD
'LDJUDPDGH%RGHL
z
z
z
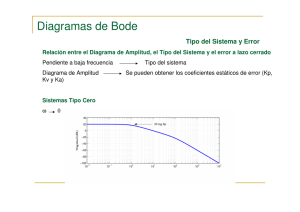
Diagrama de Bode o logarítmico, representación gráfica del logaritmo de la
magnitud M y la fase φ de una función de transferencia G(jω) frente al
logaritmo de la frecuencia ω.
Magnitud y fase se dibujan en dos gráficas separadas :
•
Logaritmo de la magnitud M (en decibelios) en función de la frecuencia ω (escala
de frecuencia logarítmica).
•
Ángulo de fase φ (generalmente en grados) en función de la frecuencia ω (escala
de frecuencia logarítmica).
El diagrama de bode permite evaluar la estabilidad relativa de un sistema
en lazo cerrado dada la respuesta en frecuencia del sistema en lazo
abierto.
Tema 5: Análisis de respuesta en frecuencia
6
5HSUHVHQWDFLyQGHODUHVSXHVWDHQ
IUHFXHQFLD
'LDJUDPDGH%RGHLL
Tema 5: Análisis de respuesta en frecuencia
7
5HSUHVHQWDFLyQGHODUHVSXHVWDHQ
IUHFXHQFLD
'LDJUDPDGH1\TXLVW RSRODUL
z
z
Diagrama de Nyquist o polar, representación gráfica:
•
de la parte real de la respuesta frecuencial de G(jω) Re{G(jω)} frente a la
parte imaginaria Imag{G(jω)}.
•
o de la magnitud M de la función de transferencia G(jω) con respecto al
ángulo de fase φ de G(jω) en coordenadas polares cuando la frecuencia
ω varía de cero a infinito.
Se consideran ángulos positivos si se miden en sentido antihorario a partir
del eje real positivo.
Tema 5: Análisis de respuesta en frecuencia
8
5HSUHVHQWDFLyQGHODUHVSXHVWD
HQIUHFXHQFLD
'LDJUDPDGH1\TXLVW RSRODULL
G(jω)
G( s ) =
ω í ’
-1
ω •
K
(T1 ⋅ s + 1) ⋅ (T2 ⋅ s + 1)
K = 10;
T1 = 0,2;
T2 = 0,5
ω ’
G( s ) =
100
2
s + 7 ⋅ s + 10
Tema 5: Análisis de respuesta en frecuencia
9
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
&ULWHULRGHHVWDELOLGDGGH1\TXLVW L
z
z
G(s)
Z = N +P
•
Z; número de ceros de 1+G(s) (número de polos del
sistema en lazo cerrado) en el semiplano derecho de s.
•
N; número de rodeos del lugar geométrico de G(jω) en el diagrama polar en sentido
horario al punto -1 + 0j .
•
P; cantidad de polos de G(s) en el semiplano derecho de s.
un sistema en lazo cerrado es estable, si y solo si, Z = 0, lo que debe implicar que
N = -P.
•
El número de polos de G(jω) en el semiplano derecho de s debe ser igual al número
rodeos del lugar geométrico de G(jω) en el diagrama polar en sentido antihorario al
punto -1 + 0j .
Tema 5: Análisis de respuesta en frecuencia
10
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
&ULWHULRGHHVWDELOLGDGGH1\TXLVW LL
G( s ) =
G(jω)
•
ω í ’
-1
K
(T1 ⋅ s + 1) ⋅ (T2 ⋅ s + 1)
K = 10;
T1 = 0,2;
T2 = 0,5
ω ω ’
100
G( s ) =
•
2
s + 7 ⋅ s + 10
Z=N+P
•
•
N=0
P=0
Z = 0 Sistema estable
Tema 5: Análisis de respuesta en frecuencia
11
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
&ULWHULRGHHVWDELOLGDGGH1\TXLVW LLL
G( s ) =
K
s ⋅ (T1 ⋅ s + 1) ⋅ (T2 ⋅ s + 1)
G(jω)
ω ’
-1
•
K = 10;
T1 = 0,2;
T2 = 0,5
ω í ’
G( s ) =
ω •
100
3
s + 7 ⋅ s 2 + 10 ⋅ s
Z=N+P
•
•
N=2
P=0
Tema 5: Análisis de respuesta en frecuencia
Z = 2 Sistema inestable
12
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
0iUJHQHVGHJDQDQFLD\IDVHL
z
z
z
La proximidad del lugar geométrico de G(jω
ω) al punto -1 + 0j en el
diagrama polar es una medida de la estabilidad relativa de un sistema
(cuanto más se acerca más oscilatoria es la respuesta del sistema).
Es una práctica común representar esta proximidad en términos de unos
valores concretos de magnitud y de fase críticos denominados:
•
Margen de ganancia.
•
Margen de fase.
Para un sistema de fase mínima, los márgenes de ganancia y fase deben ser
positivos para que el sistema sea estable. Para un rendimiento satisfactorio,
el margen de fase debe estar entre 30º y 60º, y el margen de ganancia
debe ser mayor de 6 dB.
Tema 5: Análisis de respuesta en frecuencia
13
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
0iUJHQHVGHJDQDQFLD\IDVHLL
z
Márgenes de ganancia y fase de sistemas estables
M {G(jw)} dB
•
ωpc
0 dB
MG
MG y MF positivos.
log(ω
ω)
MG
φ {G(jω
ω)}
plano G
1
-90º
-180º
,PDJ
-1
MF
5HDO
MF
log(ω
ω)
ωgc
-270º
G(jω)
Diagrama de Bode
Diagrama polar
Tema 5: Análisis de respuesta en frecuencia
14
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
0iUJHQHVGHJDQDQFLD\IDVHLLL
z
Márgenes de ganancia y fase de sistemas inestables
•
M {G(jw)} dB
0 dB
MG
MG y MF negativos.
ωgc
,PDJ
log(ω
ω)
plano G
G(jω)
MF
ω)}
φ {G(jω
1
-1
-90º
-180º
ωpc
MF
log(ω
ω)
5HDO
MG
-270º
Diagrama de Bode
Diagrama polar
Tema 5: Análisis de respuesta en frecuencia
15
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
0iUJHQHVGHJDQDQFLD\IDVHLY
z
z
z
El margen de ganancia (MG), se define como el cambio necesario en la
ganancia de un sistema en lazo abierto para que en lazo cerrado el sistema
sea inestable.
En el diagrama de Bode se mide el MG en la gráfica de magnitud como la
cantidad de dB en que la curva de magnitud excede 0 dB a la frecuencia ωpc
a la cual la curva de fase es -180º.
En el diagrama polar se mide el MG como la distancia al origen del punto de
intersección del lugar geométrico de G(jω
ω) con el eje real.
Tema 5: Análisis de respuesta en frecuencia
16
(VWDELOLGDGHQHOGRPLQLRGHOD
IUHFXHQFLD
0iUJHQHVGHJDQDQFLD\IDVHY
z
El margen de fase (MF), se define como el cambio necesario en la fase de
un sistema en lazo abierto para que en lazo cerrado el sistema sea inestable.
•
z
z
representa el retardo que se puede añadir al sistema antes de que este se
convierta en inestable. Mide la tolerancia del sistema ante retardo temporal.
En el diagrama de Bode se mide el MF en la gráfica de fase como la
cantidad en grados en que la curva de fase excede 180º a la frecuencia ωgc a
la cual la curva de magnitud es 0 dB.
En el diagrama polar se mide el MF como MF = φ -180º.
•
φ, ángulo existente entre el eje real positivo y la recta que une el origen y el punto
de intersección del lugar geométrico de G(jω
ω) con la circunferencia centrada en el
origen y de radio unidad. Ángulos positivos si se miden en sentido antihorario a
partir del eje real positivo.
Tema 5: Análisis de respuesta en frecuencia
17
(VSHFLILFDFLRQHVGHFRPSRUWDPLHQWR
HQHOGRPLQLRGHODIUHFXHQFLDL
z
z
Dado un conjunto de
especificaciones en el dominio
temporal, ¿cómo se puede
especificar la respuesta
frecuencial?
z
Ejemplo de respuesta en frecuencia de
un sistema de segundo orden
Ánalisis para un sistema de
segundo orden.
G(s) =
U(s)
Ȧn2
Y(s)
=
E(s)
s ⋅ ( s + 2 ⋅ ζ ⋅ Ȧn )
E(s)
G(s)
Y(s)
Tema 5: Análisis de respuesta en frecuencia
18
(VSHFLILFDFLRQHVGH
FRPSRUWDPLHQWRHQHOGRPLQLRGHOD
IUHFXHQFLDLL
z
z
Frecuencia de resonancia,
frecuencia ωr a la cual se logra el
máximo valor Mpω de respuesta en
frecuencia.
Mpω
Magnitud en dB
-3 dB
Ancho de banda AB, rango de
frecuencias entre los que la magnitud
de respuesta en frecuencia del
sistema en lazo cerrado no desciende
de -3 dB respecto a su valor máximo.
•
Fase en grados
En la figura: AB = ωB − 0 = ωB
ωr
Tema 5: Análisis de respuesta en frecuencia
ωB
Frecuencia (rad/seg)
Escala logarítmica
19
(VSHFLILFDFLRQHVGH
FRPSRUWDPLHQWRHQHOGRPLQLRGHOD
IUHFXHQFLDLLL
z
z
z
z
ωr y AB pueden relacionarse con la velocidad de respuesta transitoria.
AB es una medida de la posibilidad del sistema de reproducir la señal de
entrada. Especificando el AB se determina:
•
La capacidad de reproducción de la señal de entrada. Para una entrada escalón a
medida que se aumenta el AB disminuye el tiempo de subida tr de la respuesta.
•
La característica de filtrado de ruido de alta frecuencia.
Conflicto entre rapidez de respuesta y filtrado de ruido de alta frecuencia.
El valor de ωB puede relacionarse aproximadamente con la frecuencia natural
del sistema ωn.
Tema 5: Análisis de respuesta en frecuencia
20
(VSHFLILFDFLRQHVGH
FRPSRUWDPLHQWRHQHOGRPLQLRGHOD
IUHFXHQFLDLY
z
z
La sobreelongación Mp puede relacionarse con la magnitud del pico de
resonancia Mpω mediante la razón de amortiguamiento ζ. Para una entrada
escalón cuando aumenta Mpω aumenta Mp.
La especificación del error en régimen permanente también puede
relacionarse con la respuesta en frecuencia de un sistema en lazo cerrado.
•
Las constantes estáticas de error de posición Kp, velocidad Kv, y aceleración Ka
pueden deducirse de la respuesta en frecuencia del sistema.
Tema 5: Análisis de respuesta en frecuencia
21