Un sistema de control es un conjunto de subsistemas y procesos

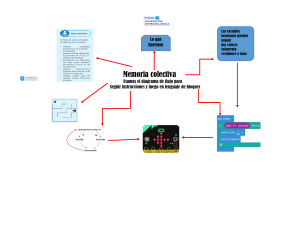
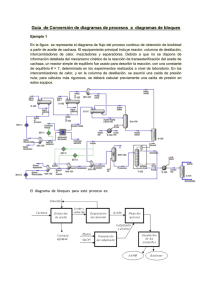
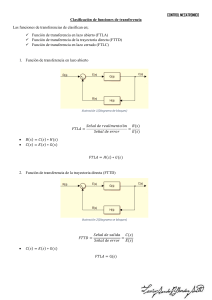
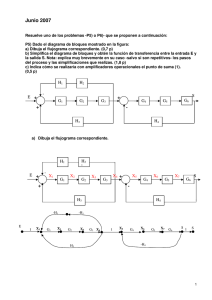
Murguia Ochoa Jaime
Ensayo 1 teoría de control I
Ingeniería de control moderna
Katsuhiko Ogata
Un sistema de control es un conjunto de subsistemas y procesos con el
fin de controlar una salida de esos procesos. Sus ventajas son que nos permite
usar cosas que de forma manual no podríamos usar por ejemplo un elevador.
En un sistema de control la entrada representa una respuesta deseada,
la salida es la respuesta real al estimulo dado de entrada, a la diferencia de la
entrada con la salida se le conoce como error de estado estable y puede se
defecto o inherente al mismo sistema.
Un sistema de lazo abierto es un sistema que no es realimentado cuenta
con la entrada de los transductores para realizar el proceso y con
perturbaciones o ruido que todo proceso de control tiene y no puede corregirlo.
El sistema de lazo cerrado (realimentado) es un sistema realimentado
con el fin de corregir errores o perturbaciones como el ruido, que en el lazo
abierto no puede medir ni comparar señales ni corregirlas.
El diseño del diagrama a bloques describe las componentes del sistema
esto es función o hardware y muestra sus interconexiones. El análisis y diseño
de un sistema de control se concentra en tres objetivos principales:



Reproducir la respuesta transitoria
Reducir los errores en estado estable
Alcanza la estabilidad
Para diseñar un sistema de control se requieren los siguientes pasos:
1. Determinación de un sistema físico y especificaciones a partir de los
requerimientos.
2. Trazo de un diagrama de bloques funcional.
3. Representación de un sistema físico mediante un diagrama
esquematizo.
4. Uso del diagrama esquemático para obtener un modelo matemático
como lo es un diagrama a bloques.
5. Reducción del diagrama a bloques.
6. Análisis y diseño del sistema para satisfacer los requerimientos y
especificaciones especiales que incluyen la estabilidad, respuesta
transitoria y desempeño en estado estable.
La función de transferencia nos permite combinar representaciones
matemáticas de los subsistemas para obtener una representación total del
sistema.
Si analizamos un sistema con la ecuación diferencial general de orden n
lineal e invariable en el tiempo, utilizando el espacio y las trasformadas de
Laplace, al cociente de la trasformada de la salida C(s) dividido entre la
transformada de la entrada R(s) a este cociente le llamamos la función de
transferencia.
Esta función también se puede aplicar para el análisis de redes pasivas
y circuitos con amplificadores operacionales sistemas mecánicos y
electromecánicos formados por resistores, capacitares e inductores siempre
con condiciones iniciales en el voltaje y en la corriente igual a cero.
Las funciones de transferencia también se obtienen por medio de las
leyes de corriente y de voltaje de Kirchhoff ya sea con el método de mallas o de
nodos.