- De los extremos de la cuerda de una polea cuelgan dos cuerpos
Anuncio
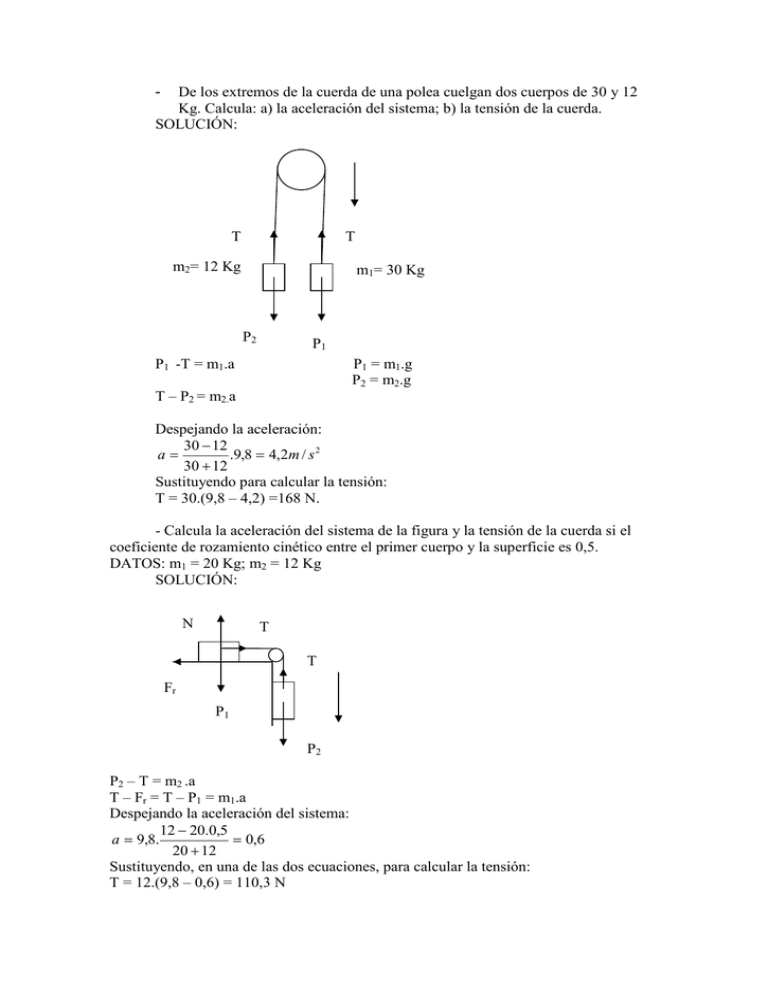
De los extremos de la cuerda de una polea cuelgan dos cuerpos de 30 y 12 Kg. Calcula: a) la aceleración del sistema; b) la tensión de la cuerda. SOLUCIÓN: - T T m2= 12 Kg m1= 30 Kg P2 P1 P1 -T = m1.a P1 = m1.g P2 = m2.g T – P2 = m2.a Despejando la aceleración: 30 − 12 a= .9,8 = 4,2m / s 2 30 + 12 Sustituyendo para calcular la tensión: T = 30.(9,8 – 4,2) =168 N. - Calcula la aceleración del sistema de la figura y la tensión de la cuerda si el coeficiente de rozamiento cinético entre el primer cuerpo y la superficie es 0,5. DATOS: m1 = 20 Kg; m2 = 12 Kg SOLUCIÓN: N T T Fr P1 P2 P2 – T = m2 .a T – Fr = T – P1 = m1.a Despejando la aceleración del sistema: 12 − 20.0,5 a = 9,8. = 0,6 20 + 12 Sustituyendo, en una de las dos ecuaciones, para calcular la tensión: T = 12.(9,8 – 0,6) = 110,3 N - Calcula la aceleración del sistema de la figura y la tensión de la cuerda si el coeficiente de rozamiento cinético entre el primer cuerpo y la superficie es 0,2. DATOS: m1 = 12 Kg; m2 = 2 Kg ; ángulo del plano 30º SOLUCIÓN: N T m1 Px T m2 Fr Py P1 P2 Suponemos que el sistema se mueve hacia la izquierda: Cuerpo 1: Px –T - Fr = m1.a Cuerpo 2: T – P2 = m2.a Resolviendo el sistema y sustituyendo: a= 9,8. 12(sen30º −0,2. cos 30º ) − 2 = 1,3 m/s2 12 + 2 Sustituyendo en cualquiera de las dos ecuaciones, calculamos la tensión: T = 2(1,3+9,8) = 22,2 N











