algebra identificando secciones conicas

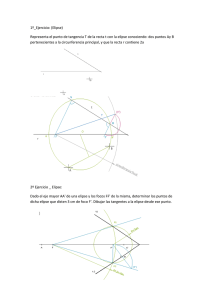
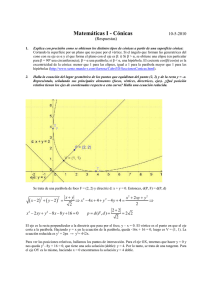
Universidad Tecnológica Centroamericana
Facultad de Ingeniería
Álgebra
Identificando Secciones Cónicas
Para identificar una sección cónica cuando esta está dada como una ecuación en
forma general, debe considerarse las siguientes características:
•
Será un círculo si hay 2 términos (x y y) al cuadrado con signo positivo y
si estos tienen el mismo coeficiente.
Ejm. 2 x 2 + 2 y 2 − 12 x + 8 y − 24 = 0
x 2 + y 2 + 4x − 4 y − 1 = 0
•
Será una parábola si existe solo un término al cuadrado, puede ser x o y.
Ejm.
y 2 − 4 y + 4x + 4 = 0
Es una parábola horizontal porque y es el término
al cuadrado.
x 2 − 4x = y + 4
Es una parábola vertical porque x es el término al
cuadrado.
•
Será una elipse si hay si hay 2 términos (x y y) al cuadrado ambos con
signo positivo y estos tienen coeficiente diferentes.
Ejms.
x 2 + 4x + 4 y 2 − 8 y + 4 = 0
2 x 2 + 3 y 2 − 8x + 6 y + 5 = 0
•
Será una hipérbola si hay 2 términos (x y y) al cuadrado uno con signo
positivo y el otro con signo negativo, además estos tendrán coeficientes
diferentes.
Ejms. 4 x 2 − y 2 − 24 x − 4 y + 16 = 0
y 2 − 4x 2 − 4 y − 8x − 4 = 0
Una vez identificado el tipo de sección cónica debe recordar las fórmulas en forma
estandar para proceder a completar al cuadrado y de ella obtener la información
necesaria para elaborar la gráfica. (Centro, radio, directriz, vértice (s), foco (s),
puntos adicionales, y asíntotas)
Círculo
( x − h) 2 + ( y − k ) 2 = r 2
Donde el centro es C(h, k) y r es el radio del círculo.
Parábola
( y − k ) 2 = 4a ( x − h)
Parábola Horizontal
( x − h) 2 = 4 a ( y − k )
Parábola Vertical
Donde el Vértice es V(h, k) y a = distancia del vértice al foco y del vértice a la
directriz.
Elipse
( x − h) 2 ( y − k ) 2
+
=1
a2
b2
Elipse Horizontal
Donde a > b > 0
( x − h) 2 ( y − k ) 2
+
=1
b2
a2
y
a2 = b2 + c2
Elipse Vertical
C(h, k) es el centro de la elipse.
a = distancia del centro a los vértices de la elipse.
b = distancia del centro a los puntos que determinan la anchura de la elipse.
c = distancia del centro a los focos de la elipse.
Hipérbola
( x − h) 2 ( y − k ) 2
−
=1
a2
b2
Hipérbola Horizontal
Donde
( y − k ) 2 ( x − h) 2
−
=1
a2
b2
a 2 = −b 2 + c 2
Hipérbola Vertical
C(h, k) es el centro de la hipérbola.
a = distancia del centro a los vértices de la hipérbola.
b = distancia del centro a los puntos que determinan la anchura de la hipérbola.
c = distancia del centro a los focos de la hipérbola.
El rectángulo que se forma para dibujar las asíntotas esta determinado por a y b .