Matemáticas I - Cónicas
Anuncio

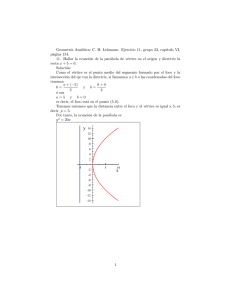
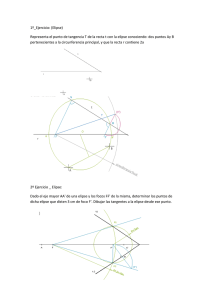
Matemáticas I - Cónicas 10-5-2010 (Respuestas) 1. Explica con precisión como se obtienen los distintos tipos de cónicas a partir de una superficie cónica: Cortando la superficie por un plano que no pase por el vértice. Si el ángulo que forman las generatrices del cono con su eje es α y el que forma el plano con el eje es β: i) Si β > α, se obtiene una elipse (en particular para β = 90º una circunferencia); β = α una parábola; si β < α, una hipérbola. El cociente cos(β)/cos(α) es la excentricidad de la cónica: menor que 1 para las elipses, igual a 1 para la parábola mayor que 1 para las hipérbolas (http://www.xente.mundo-r.com/ilarrosa/Cabri3D/SeccionesConicas.html). 2. Halla la ecuación del lugar geométrico de los puntos que equidistan del punto (2, 2) y de la recta y = -x. Represéntalo, señalando sus principales elementos (focos, vértices, directrices, ejes). ¿Qué posición relativa tienen los ejes de coordenadas respecto a esta curva? Halla una ecuación reducida. Se trata de una parábola de foco F = (2, 2) y directriz d: x + y = 0. Entonces, d(P, F) = d(P, d) ( x − 2) + ( y − 2) 2 2 = x+ y 2 ⇒ x2 − 4 x + 4 + y 2 − 4 y + 4 = x 2 − 2 xy + y 2 − 8 x − 8 y + 16 = 0 p = d (F , d ) = 2+2 2 x 2 + 2 xy + y 2 ⇒ 2 =2 2 El eje es la recta perpendicular a la directriz que pasa por el foco, y – x = 0. El vértice es el punto en que el eje corta a la parábola. Haciendo y = x en la ecuación de la parábola, queda -16x + 16 = 0, luego es V = (1, 1). La ecuación reducida es y2 = 2px → y2= 4√2x. Para ver las posiciones relativas, hallamos los puntos de intersección. Para el eje OX, tenemos que hacer y = 0 y nos queda y2 - 8y + 16 = 0, que tiene una sola solución (doble): y = 4. Por lo tanto, se trata de una tangente. Para el eje OY es lo mismo, haciendo x = 0 encontramos la solución y = 4 doble. 3. Las dos curvas de la figura comparten los mismos focos, F y F'. Para cada una de ellas, halla sus ecuaciones, las de sus asíntotas (si las tienen) y sus excentricidades. Ambas curvas reflejan todos los rayos que llegan a ellas. Considera un rayo u que parte del foco F y alcanza el punto P (cualquiera situado en la elipse, en la parte derecha del interior de la hipérbola). Traza su trayectoria hasta que vuelva a pasar por F e indica razonadamente que distancia habrá recorrido entonces. Elipse: x2/25 + y2/16 = 1, c = 3, e = 3/5 Hipérbola: a = 2, c = 3 → b = √5 x2/4 - y2/5 = 1, e = 3/2 Asíntotas: y = ±√5/2. El rayo se refleja en la elipse en el punto P hacia el foco F'. Cuando alcanza a la hipérbola en Q, se reflejará hacia el foco F. Tenemos que FP + PF' = 10 y QF' – QF = 4, por tanto recorre uns distancia de 10 – 4 = 6 unidades. http://www.xente.mundo-r.com/ilarrosa/GeoGebra/Reflexion_E_H_confocales.html. 4. Un satélite artificial rodea la Tierra en una órbita cerrada. En el perigeo (punto de máxima aproximación), se encuentra a una distancia de 20000 km, y en el apogeo (punto de máximo alejamiento) de 80000 km. Halla la excentricidad de la órbita, así como una ecuación reducida de la misma. Puedes tomar como unidad la decena de millar de kilómetros. La órbita es una elipse, en la que a – c = 2 y a + c = 8 → a = 5, c = 3 → e = 3/5, b = 4, : x2/25 + y2/16 = 1 5. Para cada uno de los tipos de cónicas, halla la longitud de la mitad de la cuerda que pasa por un foco y es perpendicular al eje, en función de los parámetros de la curva (a y b ó p). Es lo que los griegos llamaban el 'latus rectum'. En cada caso, ¿Es mayor o menor que la distancia del foco al vértice más próximo? En los tres casos se trata de la ordenada del punto en que corta a la curva una recta vertical que pasa por el foco: Parábola: y2 = 2px, F = (p/2, 0) → y2 = 2p·p/2 → y = p Elipse: x2/a2 + y2/b2 = 1, F = (c, 0) → y2 = b2(1 – c2/a2) = b2(a2 – c2)/a2 = b4/a2 → y = b2/a Hipérbola: x2/a2 - y2/b2 = 1, F = (c, 0) → y2 = b2(c2/a2 - 1) = b2(c2 – a2)/a2 = b4/a2 → y = b2/a De acuerdo con la definición de cónica que se pide en la siguiente pregunta, el vértice es siempre el punto más próximo al foco que le corresponde, pues este es el punto más próximo a la directriz. No obstante, también es muy fácil de ver directamente: Parábola: d(F, V) = p/2 < p Elipse: d(F, A) =a – c < b^2/a ↔ a2 – ac < b2 ↔ b2 + c2 – ac < b2 ↔ c2 < ac ↔ c < a Hipérbola: d(F, A) =c – a < b^2/a ↔ ac - a2 < b2 ↔ ac – a2 < c2 – a2 ↔ ac < c2 ↔ a < c 6. ¿Cómo se definen las cónicas usando la directriz? ¿Cuántas directrices tiene cada tipo de cónica? Para las elipses e hipérbolas, si llamamos s a la distancia del centro a la directriz, calcula el valor de s en función del semieje principal y la semidistancia focal (utiliza uno de los vértices) Es el lugar geométrico de los puntos del plano cuyo cociente de distancias a un punto fijo llamado foco y a una recta fija llamada directriz es constante. Esta constante es la excentricidad e de la cónica. Si e < 1 se trata de una elipse, si e = 1 de una parábola y si e > 1 de una hipérbola. Hay una directriz por cada foco: dos para elipses e hipérbolas y una para la parábola. Considerando el vértice A y su foco F y directriz d más próximos, tenemos: Elipse: e = c/a = d(A, F)/d(A, d) = (a – c)/(s – a) → s – a = (a2 – ac)/c → s = (a2 – ac)/c + ac/c = a2/c Hipérbola: e = c/a = d(A, F)/d(A, d) = (c – a)/(a – s) → a – s = (ac - a2)/c → s = ac/c - (ac - a2)/c = a2/c Si consideramos el vértice más alejado del foco F, se puede hacer de una vez para elipse e hipérbola, pues en ambos casos, d(A', F) = a + c y d(A', d) = a + s, y e = c/a = d(A', F)/d(A', d) = (a + c)/(s + a) → s + a = (a2 + ac)/c → s = (a2 + ac)/c - ac/c = a2/c Y para la elipse, si escogemos un vértice secundario es inmediato: d(B, F) = a y d(B, d) = s → e = c/a = a/s → s = a2/c ----- "Merecen ser estudiadas por si mismas" (Apolonio de Perga, ~ s. II a.c.) -----