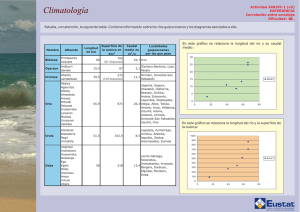
mayo-03 - IES Bachiller Sabuco

Curso 2009/10
MATEMÁTICAS, PRIMERO DE B.I.
HOJA 10. ESTADÍSTICA-2. DISTRIBUCIONES BIDIMENSIONALES
1.- Representa la nube de puntos correspondiente a esta distribución y di cuánto vale el
coeficiente de correlación.
x 1 2 3 4 5 6
y 10 8 6 4 2 0
2.- Representa la nube de puntos de esta distribución y estima cuál de estos tres puede ser el
coeficiente de correlación:
a) r=0,98
b) r=-0,87
c) r=0,5
x 0 1 2 3 3 4 5 6 7 8 9
y 1 4 6 2 4 8 6 5 3 6 9
3.- En la primera semana de noviembre, la natalidad y la mortalidad en Zaragoza vino dada
por la siguiente tabla:
Lunes Martes Miércoles Jueves Viernes Sábado Domingo
41
22
27
29
21
26
21
x=Nat.
45
39
32
34
30
110
23
y=Mor.
Calcula:
a) Las medias marginales de ambas variables.
b) Las desviaciones típicas de las dos variables.
Sol: x =26,7, y =44,7
Sol:  x =6,5,  y =27,4
c) La covarianza.
Sol:  xy =23,5
d) Representa la nube de puntos.
e) Intenta ajustarla gráficamente mediante una recta.
Sol: Y=0,55X+29,95
f) Comenta los resultados anteriores.
Sol: r=0,13, relación muy débil
4.- En la siguiente tabla se indica la edad (en años) de l0 personas adultas y el número de
horas que duermen diariamente por término medio:
Edad 50 62 85 72 60 80 75 77 55 82
Horas 8,2 7 6,3 6,5 7,3 6 6,8 6,7 7,8 6,8
Calcula:
a) Las medias marginales de ambas variables.
b) Las desviaciones típicas de las dos variables.
Sol: x =69.8, y =6.94
Sol:  x =11,56,  y =0,64
c) La covarianza. Interpretación.
Sol:  xy =-6.612, relación inversa
d) Representa la nube de puntos.
e) El coeficiente de correlación e interpreta el resultado obtenido.
Sol: r=-0.9, relación fuerte
f) La ecuación de la recta de regresión del número de horas en función de la edad.
Sol: Y=-0.05X+10,4
g) Predice el número de horas más probable que duerme una persona de 67 años.
Sol: 7,1 horas
5.- Los resultados en los exámenes de Plástica y Tecnología, de l0 estudiantes de una clase,
fueron los siguientes:
Plástica
6 2 4 5 7 7 4 9 3 4
Tecnología 4 1 7 6 9 8 3 9 4 3
Calcula el coeficiente de correlación y da una interpretación.
Sol: 0,83, relación directa y fuerte
6.- La temperatura media anual, en ºC, de varias ciudades, y el gasto medio anual en
calefacción por habitante (en miles de pesetas) fue:
Temperatura 10 12 15 16 18 22
Gasto
25 20 14 10 8 2
a) Representa la nube de puntos asociada. ¿Qué correlación observas? ¿Es fuerte?
b) Halla el coeficiente de correlación y la recta de regresión del gasto sobre la
temperatura.
c) ¿Qué gasto cabe esperar en ciudades con temperatura media de 8, 17 y 26 ºC? ¿Te
parece lógico el resultado?
7.- Se ha medido la temperatura (en ºC) y la `presión atmosférica (en mm) en una ciudad, a
la misma hora durante 7 días seguidos. Los datos fueron:
Temperatura 15 16 17 20 18 16 12
Presión
800 810 800 820 810 780 750
a) Representar estos valores en forma de nube de puntos.
b) De la representación, ¿se puede deducir el tipo de dependencia que hay entre la
temperatura y la presión?
c) Calcula el coeficiente de correlación.
d) Halla la recta de regresión de presión sobre temperatura.
8.- Las alturas, en centímetros, de 8 padres y del mayor de sus hijos varones son:
Padres 170 173 178 167 171 169 184 175
Hijos 172 177 175 170 178 169 180 187
a) Calcula la recta de regresión que permita estimar la altura de los hijos dependiendo
de la del padre.
Sol.: y=0,62x+68,19
b) ¿Qué altura cabría esperar para un hijo si su padre mide 174 cm? ¿Y para un padre,
si su hijo mide 190 cm?
Sol.: 176
c) ¿qué tipo de correlación existe entre las variables?
Sol.: directa, débil