Tarea #4 - Estadística y Probabilidad I

Estadística y Probabilidad I- CCH Sur
Octubre de 2013
Tarea #4- Datos Bivariados
1. Investiga quién fue Francis Galton y en qué consistió su Ley de Regresión Universal.
2. Investiga quién fue Karl Pearson y en que consiste el coeficiente de correlación
3. Responde a las siguientes preguntas:
a) ¿Cuál es la ecuación de una recta que pasa por dos puntos?
b) Encuentre las ecuaciones de las rectas que pasan por los siguientes puntos y dibújelas:
{(4, 7) y (16, 24)} y {(-1,3) y (1, 1)}.
c) ¿Cuál es la recta que mejor se ajusta a una nube de puntos?
4. Una cadena de restaurantes de comida rápida decide llevar a cabo un experimento para
medir la influencia sobre las ventas del gasto en publicidad. En ocho regiones del país, se
realizaron diferentes variaciones relativas en el gasto en publicidad, comparado con el año
anterior, y se observaron las variaciones en los niveles de ventas resultantes. La tabla
adjunta muestra los resultados.
Incremento del Gasto 0
en Publicidad (%)
Incremento en las 2,4
Ventas (%)
4
14
10
9
8
6
1
7,2
10,3
9,1
10,2
4,1
7,6
3,5
a) Dibuje la nube de puntos correspondiente.
b) Para un modelo de regresión lineal simple, obtenga la recta de regresión ajustada
y grafíquela sobre (a)
c) Calcula el coeficiente de correlación. Analiza la correlación entre ambas variables
d) Si el incremento en publicidad hubiese sido 12%, ¿cuál sería el incremento de ventas
estimado?
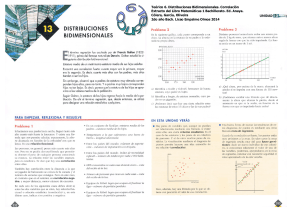
5. Asocia las rectas de regresión y = 2x – 12, y = 0,5x + 5, y = –x +16 a las nubes de
puntos siguientes:
6. Asigna los coeficientes de correlación lineal r = 0,4, r = –0,85 y r = 0,7, a las nubes del
problema anterior.