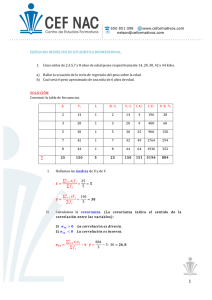
Estadística bidimensional 1 Regresión y correlación

Estadística bidimensional 1
Regresión y correlación
En las distribuciones bidimensionales se estudian dos conjuntos de datos que varían a la vez, cada elemento de la
distribución está definido por dos valores (x,y). Lo que interesa es estudiar la posible relación entre las dos variables.
Se da una relación funcional entre dos variables, cuando al determinar una de ellas la otra queda unívocamente
determinada.
Se da una relación estadística o correlación, entre dos variables, cuando al determinar una la otra queda
determinada en términos de probabilidad, es decir, es probable que la segunda variable tome valores próximos a uno
esperado.
Cuando representamos gráficamente una distribución bidimensional en un sistema cartesiano obtenemos lo que llamamos
diagrama de dispersión ó nube de puntos.
La forma que adopta la nube de puntos nos indica el tipo y grado de relación o dependencia entre ambas variables.
Hablaremos de correlación lineal cuando los datos tienden a agruparse alrededor de una recta.
Si esta recta tiene pendiente positiva la correlación o dependencia es directa, incrementos positivos en una variable
implican aumentos en la otra.
Si la recta tiene pendiente negativa la correlación o dependencia es inversa, al aumentar una disminuye la otra.
Correlación lineal
La covarianza es una medida de la dependencia estadística entre dos variables.
Se calcula mediante la fórmula:
(*aquí ni=1 y n=nº de pares observados)
El signo de la covarianza determina el sentido de la correlación. Si calculamos el centro
de gravedad de la nube puntos (x,y) y trazamos unos nuevos ejes coordenados por ese
punto, vemos que si la mayoría de los puntos están en el primer y tercer cuadrante
muchos productos (xi-x)·(yi-y) son positivos y la covarianza es positiva; y viceversa si la
mayoría están en el 2º y 4º cuadrante que será negativa.
Aún así resulta difícil interpretar el valor de la covarianza por lo que se calcula el
Coeficiente de correlación lineal:
Este coeficiente, llamado de Pearson, es una medida objetiva de la correlación lineal entre dos variables.
Su valor está entre -1 y 1.
Su signo es el de la covarianza, si r>0 la correlación es directa, si r<0 inversa.
Si se aproxima a -1 ó a 1 la correlación es fuerte, si está próximo a 0 es débil.
Cuando vale -1 ó 1 es perfecta, los puntos están situados en una recta.
La recta de regresión
Llamamos linea de regresión a la curva que mejor se ajusta a nube de puntos,
es una curva ideal en torno a la que se distribuyen los puntos de la nube.
Se utiliza para predecir la variable dependiente (Y) a partir de la independiente
(X).
La diferencia entre el valor real (yi) y el teórico (yi*) se llama residuo.
En nuestro caso esta linea es una recta que se calcula imponiendo dos
condiciones:
Debe pasar por el punto (x,y), centro de gravedad de la distribución.
La suma de los cuadrados de los residuos debe ser mínima.
Con esto obtenemos la ecuación de la
RECTA de REGRESIÓN de Y sobre X:
La pendiente de esta recta es el llamado
COEFICIENTE de REGRESIÓN=
NOTA: Si lo que deseamos es predecir el valor de X, habremos de calcular
otra recta de regresión, análoga a la anterior, intercambiando las x con las
y.
MATEMÁTICAS 1º
Mª José García Cebrian, 2006