Elipse con centro en el origen

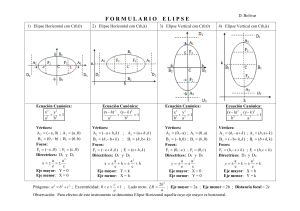
ELIPSE
Definición.- Una elipse es el lugar geométrico de un punto que se mueve en un plano de tal manera
que la suma de sus distancias a dos puntos fijos de ese plano (Focos) es siempre igual a una constante
(2a).
Elementos de una elipse.- Entre los más importantes están:

Centro “C”.- Punto medio entre los focos (F y F’) o entre los vértices (V y V’).

Focos “F” y “F’ ”.- Puntos fijos de la elipse que se encuentran sobre el eje mayor.

Vértices “V” y “V’ ”.- Extremos del eje mayor que indican el largo de la elipse.

Vértices Secundarios “A” y “A’ ”.- Extremos del eje menor que indican el ancho de la elipse.

Parámetro “a”.- Distancia entre el Centro y el Vértice.

Parámetro “b”.- Distancia entre el Centro y el Vértice Secundario.

Parámetro “c”.- Distancia entre el Centro y el Foco.

Eje Mayor “2a”.- Distancia entre los vértices V y V’.

Eje Menor “2b”.- Distancia entre los vértices secundarios A y A’.

Lado Recto “LR”.- Segmento perpendicular al eje mayor que pasa por el foco.

Excentricidad “e”.- Razón entre los parámetros “c” y “a”, indica la relación entre el largo y ancho
de la elipse, siendo siempre menor a 1.
Elipses con centro en el origen.- Estas pueden ser:

horizontales si “x” se relaciona con “a” (parámetro mayor) y la “y” se relaciona con “b”
(parámetro menor)

verticales si “x” se relaciona con “b” (parámetro menor) y la “y” se relaciona con “a”
(parámetro mayor)
Elipse horizontal con centro en el origen
Ecuación:
Parámetros:
𝑥2
𝑦2
𝑎
𝑏2
=1
𝑎2 = 𝑏 2 + 𝑐 2
Excentricidad: 𝑒
Lado Recto:
2 +
=
𝑐
𝑎
𝐿𝑅 =
2𝑏2
𝑎
Elipse vertical con centro en el origen
Ecuación:
Parámetros:
𝑥2
𝑏2
𝑎2
=1
𝑎2 = 𝑏 2 + 𝑐 2
Excentricidad: 𝑒
Lado Recto:
+
𝑦2
=
𝑐
𝑎
𝐿𝑅 =
2𝑏2
𝑎