Integral Indefinida: Primitivas y Propiedades

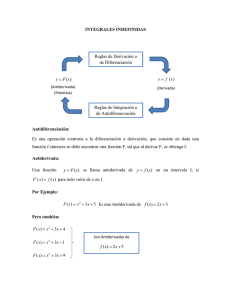
UNIVERSIDAD NACIONAL DE SAN MARTÍN
FACULTAD INGENIERÍA CIVIL Y ARQUITECTURA
DEPARTAMENTO ACADÉMICO DE INGENIERÍA Y ARQUITECTURA
ÁREA DE MATEMÁTICA
Docente: Lic. JOSÉ ENRRIQUE GUZMÁN ANTICONA
Curso: ANÁLISIS MATEMÁTICO II - FIC
Tema: INTEGRAL INDEFINIDA
Semana: 01
2023 – II
Primitivas o Antiderivadas
Definición: Una función F se llama antiderivada de una
función f en un intervalo I, si la derivada de F es f; esto
es: F´(x) = f(x) para todo x en I.
Observación:
De la definición se ve que F no es única.
Para que F´(x) exista, la función F(x) debe ser continua.
Teorema
Si F es una antiderivada de f en un intervalo I, la
antiderivada más general de f en I es:
F (x)+ C
donde C es una constante arbitraria.
Ejemplo:
Hallar la antiderivada de la función:
1. f(x) = 3x2
2. f(x) = cosx
Solución:
Solución:
F(x) = x3 + 1
F(x) = cosx - 10
F(x) = x3 – 1
F(x) = cosx + 2
F(x) = x3 + 2
F(x) = cosx + C
F(x) = x3 – 2
F(x) = x3
F(x) = x3 + C
Interpretación geométrica
5
5
2
1
1
5
2
2
1
1
5
2
Interpretación geométrica
5
2
1
5
1
5
2
2
1
1
5
2
El conjunto de todas las antiderivadas se
denomina: la Integral Indefinida de f
respecto a x, denotada por:
Diferencial de x
f
(
x
)
dx

F
(
x
)

C

Símbolo de
Integral
Función
integrando
Una antiderivada de f
Constante de
integración
Ejemplo
Calcular:
1 .  x2 dx
3. 
1
4x
2
dx
Solución:
Solución:
Usando la fórmula 2 de integrales inmediatas:
Usando la fórmula 23 de integrales inmediatas:
x 2 1
 x dx  2  1 + C
2
x3

+C
3
1
1
 4  x2 dx   22  x2 dx

1
x
arctg + C
2
2
PROPIEDADES DE LA INTEGRAL
INDEFINIDA
1. De la suma o diferencia:
  f ( x)  g ( x) dx   f ( x)dx   g ( x)dx
2. Del múltiplo constante:
kf
(
x
)
dx

k
f
(
x
)
dx


NOTA:
 f ( x) g ( x)dx   f ( x)dx  g ( x)dx
Ejemplos:
Usando la integración directa mediante las propiedades, calcular:
2

1 .   3senx  4e x  dx
x


Solución:


2
x
  3senx  4e  dx
x


2
2
dx 
x

Usando propiedad 1 :
 3senx dx   4ex dx Usando propiedad 2 :
1
dx  3 senx dx  4 e x dx
x
For. 3

For. 6

For. 4
= 2Ln|x| + 3(-cosx) – 4ex + C
2.
(1  x)3
 x3x
dx
Solución:
Desarrollando el numerador y reduciendo términos en el denominador se obtiene:
(1  x)3
 x3x
dx 

1  3x  3x2  x3
x
4 /3
dx
Dividiendo el numerador entre el denominador término a término se obtiene:

 1
3x
3x2
x3 




dx
4 /3
4 /3
4 /3 
 x4 / 3
x
x
x


Ahora usamos teoría de exponentes:
 x
4 / 3

 3x 1 / 3  3x2 / 3  x5 / 3 dx
Aplicando propiedades y formula 2, se tiene:
9x 2 / 3
9 x5 / 3
3x 8 / 3
 



+C
1/3
2
5
8
x
3