13-DESCARGAR-DIVISIBILIDAD-PARA-ESTUDIANTES-DE-PRIMERO-DE-SECUNDARIA

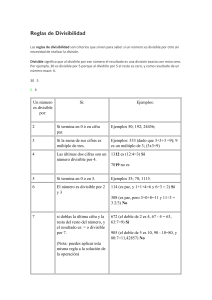
Divisibilidad I
La divisibilidad es una parte de la teoría de los números
que analiza las condiciones que debe tener un número para
que sea divisible por otro.
¿Y cuándo un número es divisible por otro? se dice que
"A" es divisible por "B", si al dividir "A" entre "B" la división
resulta EXACTA (cociente entero y residuo cero).
"A" es divisible por "B"
A
0
d) 7 :
e) 13 :
2. DIVISOR DE UN NÚMERO
Un número "B" es divisor de "A", si "B" está contenido
en "A" un número exacto de veces. Los divisores también
reciben el nombre de FACTORES.
B
q
Cociente entero
Residuo cero
Ejemplos:
a. 13 es divisor de 39
b. 5 es divisor de 20
Ejemplos:
a. 91 es divisible por 7; pues:
91 7
0 13
* Ejercicios: Hallar todos los divisores de:
a) 12 :
b) 18 :
b. 143 es divisible por 11; pues:
143 11
33 13
c) 20 :
0
d) 24 :
Dos conceptos fundamentales en DIVISIBILIDAD son:
1. MÚLTIPLO DE UN NÚMERO
"Un número "A" es múltiplo de otro "B", si "A" contiene a "B"
un número exacto y entero de veces".
e) 72 :
Observaciones:
1. Todo número tiene INFINITOS MÚLTIPLOS.
2. Todo número tiene una cantidad FINITA DE
DIVISORES o FACTORES.
Ejemplos:
a. 91 es múltiplo de 7, pues: 91 = 13 (7)
b. 111 es múltiplo de 37, pues: 111 = 3(37)
3. El número UNO es DIVISOR o FACTOR de todos los
números.
· Notación:
4. El CERO es múltiplo de todos los números.
o
AB
En resumen:
Se lee:
"A" es múltiplo de "B"
Nótese que: "A" es divisible por "B"
* Ejercicios: Escribe los primeros 10 múltiplos de:
a) 3 :
b) 2 :
c) 5 :
o
AB
Se lee:
"A" es múltiplo de "B"
"A" es divisible por "B"
"B" es divisor de "A"
"B" es factor de "A"
Problemas para la clase
o
Nivel I
8. Del 1 al 100, ¿cuántos números son 5 ?
1. Indicar verdadero (V) o falso (F) según corresponda:
a) 18
d) 21
o
a) 35  5 ................................( )
b) 19
e) 22
c) 20
o
o
9. Del 1 al 80, ¿cuántos números son 3 ?
b) 5  15 ................................ ( )
o
c) 48  4 ............................... ( )
a) 24
d) 27
o
d) 111  3 .............................. ( )
o
b) 25
e) 28
c) 26
o
e) 48  9 ............................... ( )
10.Del 1 al 500, ¿cuántos números son 23 ?
o
f) 10  1000 .......................... ( )
a) 25
d) 22
2. ¿Cuántos números de una cifra son divisibles por 3?
a) 1
d) 4
b) 2
e) 5
b) 10
e) 7
c) 9
Ejemplos:
a) 24 no es múltiplo de 5, pues:
24 5
4 4
4. El mayor número de dos cifras es un múltiplo de:
a) 2
d) 5
b) 3
e) 6
c) 23
Observación
Si un número no es divisible por otro, entonces se podrá
encontrar su residuo.
c) 3
3. ¿Cuántos números de dos cifras son divisibles por 11?
a) 11
d) 8
b) 24
e) 21
c) 4
residuo
o
se puede escribir: 24  5  4
5. Relaciona correctamente:
o
o
o
o
b) 28  9  1 ó 28  9  8
c) 35  8  3 ó 35  8  5
91
• Es un múltiplo de 8
1 155
• Es un múltiplo de 3
Nivel II
2 000
• Es un múltiplo de 13
1. Escribir verdadero (V) o falso (F), según corresponda:
1 941
• Es un múltiplo de 11
o
o
6. Indicar la suma de cifras del mayor número que sea 8
I. 648
III. 2 008
a) 25  7  3 ...................( )
o
b) 32  9  5 ...................( )
II. 1 000
IV. 7 580
o
a) 18
d) 20
b) 1
e) 19
c) 10
c) 51  5  4 ....................( )
o
7. Si el siguiente número 453 x es divisible por 7, calcular
el valor de "x".
a) 7
d) 4
b) 6
e) 3
d) 90  7  1 ....................( )
o
e) 87  10  7 ..................( )
c) 5
o
f) 101  9  3 ..................( )
2. Hallar un valor de "x", si:
6. Si el siguiente número 743b es divisible por 9, calcular
el valor de "b".
o
128  11  x
a) 4
d) 7
b) 5
e) 8
a) 4
d) 3
c) 6
b) 5
e) 22
c) 6
o
3. Si el número 92a es múltiplo de 13 más 5, calcular "a".
a) 8
d) 9
b) 7
e) 11
7. ¿Cuántos números desde el 1 hasta el 32 son 4  1 ?
a) 5
d) 8
c) 6
b) 6
e) 28
c) 7
o
4. Si el siguiente número 162a es divisible por 8, ¿cuál es
el valor de "a"?
a) 5
d) 6
b) 4
e) 7
c) 3
o
III. 878
IV. 753
a) Sólo I
d) I y III
b) Sólo II
e) I y IV
a) 9
d) 11
b) 8
e) 10
c) 7
9. Calcular la suma de los 8 primeros múltiplos de 3.
5. Indicar cuál de los siguientes números son 7  3
I. 87
II. 714
8. ¿Cuántos números del 1 al 100 son 9  3 ?
a) 84
d) 96
b) 24
e) 54
c) 108
o
10.Del 100 al 3 600, determine cuántos son 40
c) Sólo III
a) 88
d) 120
b) 68
e) 100
c) 90
Divisibilidad II
Problemas para la clase
Nivel I
1. Hallar el valor del dígito "a" en la siguiente ecuación:
o
b) 30
e) 25
c) 35
2. Un avión se dirige de Lima al Cusco con 200 pasajeros
8a  1  7
2. Si "a" representa a una cifra, hallar su valor en:
o
7a  5  9
3. Si: a < 10, hallar la suma de valores que puede tomar en:
o
3a  1  7
4. Si:
entre nacionales y extranjeros. De los extranjeros, se
2
4
1
sabe que los
son europeos, los
usan lentes y
7
5
3
hablan español. ¿Cuántos extranjeros viajan?
a) 100
d) 115
b) 95
e) 90
c) 105
3. En el problema anterior, ¿cuántos extranjeros no hablan
español?
o
(5  a)  7  3  5
hallar el menor valor que puede tomar "a" (a  lN ).
5. Hallar el menor dígito "p" que cumpla:
o
3p  19  4
a) 35
d) 90
b) 60
e) 50
c) 70
4. En el aula del 1er año "C" son 45 alumnos y se sabe que
4
estudiaron su primaria en TRILCE y a
7
los 2 les gusta la aritmética. ¿Cuántos hombres hay en
3
dicho salón?
de las mujeres
6. Hallar el menor dígito "a" que cumpla:
o
118a  271  11
7. Hallar "a", sabiendo que es menor que 10, en:
o
83a  40  13
a) 21
d) 42
b) 23
e) 24
c) 35
5. Con las siguientes pistas, descubre ¿cuántas canicas
tiene Luis?
8. Hallar "n", si se cumple:
o
- Tiene menos de 100 pero más de 5 decenas.
- Si los cuenta de 5 en 5 no sobra ninguno.
- Si hace grupos de 11 le sobran 3.
o
a) 25
d) 80
127n  17
9. Hallar "p", si se cumple:
35p9  13
10.Calcular "a", si se cumple que:
o
1a  2a  3a  4a  7
Nivel II
1. A una fiesta acudieron 100 personas y se sabe que los
3
de los hombres son casados, además la quinta parte
13
de los hombres usan lentes. ¿Cuántas mujeres asistieron
a dicha reunión?
a) 65
d) 60
b) 70
e) 90
c) 60
6. En el aula del 1er año de Trilce, hay más de 20 pero
menos de 50 alumnos. El profesor de aritmética observó
que si hace grupos de 2 sobra 1, si los agrupa de 3 en
3 también sobra 1; lo mismo sucede si hace grupos de
4 ó de 6, siempre sobra 1. Pero si hace grupos de 7 no
sobraría ningún alumno. ¿Cuántos alumnos hay en dicha
aula?
a) 14
d) 42
b) 35
e) 49
c) 28
1
AÑO
7. En el último examen de admisión a la UNMSM ingresaron
350 alumnos a la facultad de derecho. De ellos se sabe
2
que los
de los varones postulaban por tercera vez;
7
4
5
de los varones son menores de edad y los
de los
5
6
varones se prepararon en TRILCE. ¿Cuántos varones
ingresaron a esa facultad?
3. Hallar "a", si se cumple:
o
2a42  17
a) 0
d) 3
b) 1
e) 4
c) 2
4. Hallar "a", si:
o
1a12  40  13
a) 105
d) 210
b) 140
e) 120
c) 175
a) 1
d) 4
8. En el problema anterior, ¿cuántos de los varones que
ingresaron no se prepararon en TRILCE?
b) 6
e) 5
c) 3
5. Hallar "p" si:
o
a) 15
d) 40
b) 25
e) 180
c) 35
9. A una fiesta acudieron más de 100 personas pero menos
3
de 200. Se sabe además que los
fueron con jean,
5
2
3
los
con zapatillas y los
se retiraron antes de la
7
4
media noche. ¿Cuántas personas asistieron?
a) 100
d) 140
b) 105
e) N.A.
17p1  777  7
c) 135
a) 5
d) 9
b) 4
e) 3
c) 7
6. Hallar "a" si:
o
1a  2a  3a  4a  5a  37
a) 1
d) 7
b) 3
e) 9
c) 5
7. Calcular "a", si se cumple:
o
10.En el problema anterior, ¿cuántas personas fueron con
1a  2a  3a  ...  9a  13
zapatillas?
a) 20
d) 80
b) 40
e) 90
c) 60
a) 3
d) 7
b) 4
e) 2
c) 5
8. Calcular "a", si se cumple:
Nivel III
o
1a  2a  3a  ...  9a  7
1. Un buen hombre llevaba 198 canicas para ser repartidos
entre sus nueve sobrinos, pero antes de llegar a casa
de ellos se encontró con un niño pobre al que le regaló
más de 30 pero menos de 40 canicas. ¿Cuántas le regaló
a) 3
d) 9
o
275a  448  9
repartirlo exactamente entre sus sobrinos?
b) 34
d) 36
e) 38
c) 35
c) 8
9. Halla a<10, si se cumple:
al niño exactamente, si lo que le quedó alcanzó para
a) 32
b) 4
e) 6
a) 1
d) 5
b) 2
e) 4
c) 3
10.Hallar la suma de los valores ab que cumplan:
2. Cierto día el profesor Lucho llevaba 741 caramelos para
o
45ab  19  3
repartirlos entre sus 13 mejores alumnos. Antes del
reparto retiró más de 80 pero menos de 100 caramelos
y los que quedaron alcanzaron para todos en partes
iguales. ¿Cuántos caramelos retiró el profesor?
a) 81
b) 83
d) 91
e) 99
c) 89
a) 148
d) 98
b) 236
e) 220
c) 168
Divisibilidad III
CRITERIOS DE DIVISIBILIDAD
 Problema resuelto
Para saber en forma inmediata si un número es divisible
entre otro, en algunos casos no es necesario efectuar la
división correspondiente, porque bastará conocer algunas
características de tal situación de divisibilidad; a estas
características las conocemos como criterios de divisibilidad
y son los siguientes:
 DIVISIBILIDAD POR 2
Un número es divisible por 2 cuando su última cifra es
CERO o PAR.
1. Hallar el valor de "x", sabiendo que 4x327 es divisible
por 9.
Solución:
o
o
Si: 4x327  9  4 + x + 3 + 2 + 7 = 9
o
x + 16 = 9
Y como "x" es una cifra: x = 2, pues: 2 + 16 = 18 (que
o
es un 9 )
o
abcd  2  d  0; 2; 4; 6 u 8
 DIVISIBILIDAD POR 4
Un número es divisible por cuatro, cuando las dos
últimas cifras del numeral forman un múltiplo de cuatro
o
 DIVISIBILIDAD POR 5
Un número es divisible por 5, cuando su última cifra es
0 ó 5.
o
abcd  5  d  0 ó d  5
 DIVISIBILIDAD POR 25
Un número es divisible por 25, si sus dos últimas cifras
o
abcde  4  de  4
o
forman un 25 o terminan en dos ceros.
 DIVISIBILIDAD POR 8
Un número es divisible por ocho, cuando sus tres últimas
cifras del numeral forman un múltiplo de ocho.
o
o
o
abcd  25  cd  00; 25; 50 ó 75
 Problema resuelto
abcde  8  cde  8
 DIVISIBILIDAD POR 3 ó 9
Un número es divisible entre 3 ó 9, si y sólo si la suma
de sus cifras es divisible entre 3 ó 9 respectivamente.
1. Hallar la suma de valores de "x", si 351x5 es divisible
por 25.
Solución:
o
o
Si: 351x5  25  x5  25 de donde: x = 2 ó x = 7
o
o
o
o
abcd  3  a  b  c  d  3
 La suma de valores: 2 + 7 = 9
abcd  9  a  b  c  d  9
 DIVISIBILIDAD POR 6
Un número es divisible por 6 si lo es por 2 y 3 a la vez.
Ejemplos:
o
o
a) ¿35 184 es 3 ? ¿y 9 ?
o
o
De "3": sí, porque: 3 + 5 + 1 + 8 + 4 = 21 y 21 = 3
o
De "9": no, porque: 21  9
o
o
abcd 6  d  0; 2; 4; 6 u 8 y además: a  b  c  d  3
Ejemplo:
o
a) ¿51 372 es 6 ?
Veamos:
o
b) ¿35 874 es 3 ? ¿y 9 ?
o
o
De "3": sí, pues: 3 + 5 + 8 + 7 + 4 = 27 = 3
o
De "9": sí, pues: 27  9
¿Es 2 ? Sí, pues termina en cifra par
o
o
¿Es 3 ? Sí, pues: 5 + 1 + 3 + 7 + 2 = 18 = 3
1
AÑO
 DIVISIBILIDAD POR 7
Un número será divisible por 7 si cumple con la siguiente
regla:
* Multiplicamos cada una de las cifras del número dado
de derecha a izquierda por los siguientes factores:
Ojo: si luego de restar obtenemos aún un número
grande, repetimos el procedimiento.
Ejemplo: ¿Es 626934 divisible por 7?
Veamos:
1; 3; 2; - 1; - 3; - 2; 1; 3; 2; - 1; - 3; - 2; ... etc.
* Sumamos los números enteros obtenidos. Si el
resultado final es CERO o múltiplo de 7, el número
dado será entonces divisible por 7.
Ejemplo:
¿Es 626 934 divisible por 7?
62693 4 8
6268 5 10
625 8 16
60 9 18
42 = 7
Luego, 626934 es divisible por 7.
Veamos:
6
2
6
9
3
4
-2
-3
-1
2
3
1
-12
-6
-6 +18 +9 +4
DIVISIBILIDAD POR 11
Un número será divisible por 11 si la suma de sus
cifras de orden impar (empezando por la derecha)
menos la suma de las cifras de orden par, resulta ser
cero o múltiplo de 11.
Ejemplo:
¿Es 9 873 226 divisible por 11?
Sumando los enteros obtenidos:
- 12 - 6 - 6 + 18 + 9 + 4 = 7
* Sumemos primero las cifras de orden impar a partir
de la cifra de las unidades:
6+2+7+9 = 24 ... (1)
Luego, 626 934 es divisible por 7.
* Otro método:
Un número es divisible por 7, si cuando al número de
decenas del número le restamos el doble de su cifra de
unidades resulta un número multiplo de 7.
* Sumemos luego las cifras de orden par a partir de la
cifra de las decenas:
2+3+8 = 13 ... (2)
* Restemos ahora (1) - (2): 24 - 13 = 11
* Luego, 9 873 226 es divisible por 11.
Problemas para la clase
Nivel I
1. Si se tienen los siguientes números: 12; 24; 38 y 41,
decir cuál o cuáles son divisibles por 2.
a) 12 y 24
c) 24 y 38
e) Ninguno
b) 24 y 41
d) 12; 24 y 38
2. Si se tiene los números 124; 233; 666 y 429, ¿cuántos
son divisibles por 3?
a) 0
d) 3
b) 1
e) 4
c) 2
3. Si se tienen los números: 48; 64; 1 200 y 5 600, ¿cuántos
o
son 4 ?
a) 0
d) 3
b) 1
e) 4
c) 2
4. Si se tienen los números:
a0; c5; d00; bmn0
¿cuántos son divisibles por 5?.
a) 0
d) 3
b) 1
e) 4
c) 2
a) 6
d) 9
5. Si se tienen los números:
I. 12 345
II. 43 927
III. 78 900 991
o
2nnmx  2
b) Sólo II
e) Ninguno
c) Sólo III
a) 10
d) 18
b) 12
e) 6
a) 1 000
c) 2 410
e) Ninguno
b) 1 000 y 2 410
d) 2 420
7. Calcular cuánto debe de valer “a” para que el numeral
sea divisible por 9.
2345a
b) 0
e) 4
c) 6
8. Calcular cuánto debe de valer “a” para que el numeral
sea divisible por 5.
2a00a
a) 0 ó 5
d) 2
b) 0
e) 8
c) 5
9. ¿Cuánto debe de valer “x” para que el numeral sea
divisible por 4?
12383x
a) 2 ó 4
d) 2 ó 6
b) 0
e) 6
c) 4
a) 25
d) 20
b) 24
e) 18
c) 23
5. Hallar el mayor valor que puede tomar ab , si:
o
272mab  25
a) 00
d) 85
b) 25
e) 75
c) 50
6. Calcular el valor de “a”, si: 2a45a es divisible por 8.
a) 6
d) 3
b) 5
e) 2
c) 4
o
7. Calcular "a + b", si: 54a2ab  125
a) 0
d) 6
b) 4
e) 9
c) 5
que puede tomar “a” en:
o
4a21  3
a) 10
d) 7
º
aa682  3
b) 2
e) 6
o
29a2  4
8. Calcular la suma del mayor valor más el menor valor
10. Hallar el menor valor de “a”, si:
a) 1
d) 5
c) 20
4. Hallar la suma de valores de “a”, si:
6. Se tiene los números: 1 000, 2 410 y 2 420. ¿Cuál de
los números es divisible por 8?.
a) 5
d) 9
c) 8
3. Hallar la suma de valores de “x”, si:
¿cuál o cuáles son divisibles por 9?.
a) Sólo I
d) I y II
b) 7
e) 2
c) 3
b) 3
e) 13
c) 15
9. Calcular “A + B”, si:
o
A = Suma de valores de “a” en: 5a2  9
o
Nivel II
B = Suma de valores de “b” en: ba4  3
1. Hallar el valor de “a” para que el numeral sea divisible
por 11
a) 12
d) 18
234a
a) 2
d) 4
b) 3
e) 6
c) 16
10.Determine el valor de “a” en:
c) 0
2. Calcular el valor de “a” para que el numeral sea divisible
por 7
7439a
b) 15
e) 20
o
5a2a3  11
a) 2
d) 4
b) 9
e) 5
c) 3
Nivel III
7. Hallar la suma de valores de “a”, en:
o
1. Determinar el valor de “m”, si: m2(m  2)34
es divisible por 11.
a) 6
d) 5
b) 9
e) 4
c) 7
o
c) 28
a) 2
d) 5
b) 1
e) 6
c) 3
o
a) 2
d) 8
o
b) 2
e) 6
c) 7
o
9. Dar el valor de "a + b", si: 6a(a  3)3  9 , 2a3bbb  11
3. Calcular “a”, si: 3a5a243  9
a) 3
d) 5
b) 10
e) 4
o
o
b) 36
e) 0
a) 5
d) 8
8. Hallar “n”, si: 9923n  11
2. Calcular: a2 - b2, si: a892  9 y 4b97  11
a) 40
d) 12
2aa6  8
c) 4
b) 5
e) 7
c) 4
o
10. Calcular “a”, si: 2a543  9
4. Calcular el residuo de dividir:
a) 3
d) 7
222
... 22

 entre 9
b) 4
e) 9
c) 6
40 cifras
a) 6
d) 9
b) 8
e) 0
11.Calcular el resto de dividir: 2323
... 23

 entre 9
c) 1
12 cifras
a) 2
d) 7
o
5. Hallar el valor de “n”, si: nn2n3n  8
a) 2
d) 4
b) 1
e) 8
12. Si: 8a43b8 es igual a 9 , y además se sabe que: a - b = 5,
hallar “a”.
a) 3
d) 8
o
A = Suma de valores de “a” en: a2  4
o
B = Suma de valores de “b” en: ba2b  5
b) 15
e) 30
c) 5
o
c) 5
6. Hallar “A - B”, si:
a) 20
d) 28
b) 4
e) 3
c) 25
b) 4
e) 9
c) 7