3 1 TRIGONOMETRíA 3 El libro de TRIGONOMETRÍA 3, para el tercer año de educación secundaria, se complementa con el CUADERNO DE TRABAJO TRIGONOMETRÍA 3 y ha sido elaborado por el Departamento Académico de la Editorial Ingenio & YHO S.A.C. ubicado en Av. Tacna 407 interior 301 Cercado de Lima, Lima. Título de la obra: Título de la colección: Director Académico: Editores Responsables: Cuaderno de trabajo Trigonometría 3 Geniomatic Educación Secundaria Hernán Hernández Bautista Hernán Hernández Bautista Anibal Trucios Espinoza Asesor Académico: Anibal Trucios Espinoza Diseño y diagramación: Katherine Karen Rivera Escuel Marco Antonio Lizárraga Podestá Eduardo Tomas Granados Marcelo Norma Guadalupe Guerrero Noel Corrección de estilo: Victor Francisco Bautista Victor Emilio Ventura Bismarck Fotografía: Yuri Hernández Oblea Hernán Hernández Bautista Páginas web Primera edición: Setiembre 2015 Tiraje: 4000 ejemplares Editado e impreso en los talleres gráficos de: Editorial Ingenio & YHO S.A.C. Av. Tacna N° 407 Of. 301 - Lima Telefax: (511) 426–4853 www.editorialingenio.pe E-mail: [email protected] Impreso en Octubre 2015 Copyright © 2015 Geniomátic E.I.R.L. Prohibida la reproducción total o parcial de este libro, por cualquier medio. Número de Proyecto Editorial: 31501001501087 Hecho el Depósito Legal en la Biblioteca Nacional del Perú N° 2015-14418 ISBN: 978-612-4302-12-1 PRESENTACIÓN AL MAESTRO: El Estado peruano dirige la política educativa a través del Ministerio de Educación. Sin embargo, la tarea educativa es responsabilidad de todos los peruanos, en especial de los profesores, los alumnos, las autoridades docentes y los padres de familia. El Diseño Curricular Nacional (DCN) de Educación Básica Regular, formulado por el Ministerio de Educación, fija el marco de nuestro trabajo educativo, labor que desarrollamos con los textos escolares de Matemática Geniomátic de educación secundaria. Compartimos la propuesta de “ofrecer una educación integral a los estudiantes mediante una formación científica, humanística y técnica. Afianzar su identidad personal social. Profundizar los aprendizajes logrados en el nivel de Educación Primaria. Orientar al desarrollo de capacidades que permitan al educando acceder a conocimientos humanísticos, científicos y tecnológicos en permanente cambio. Formar para la vida, el trabajo, la convivencia democrática, el ejercicio de la ciudadanía y para niveles superiores de estudio. Tenemos en cuenta las características, las necesidades y los derechos de los púberes y adolescentes“. La labor docente, particularmente en Matemática, es una tarea apremiante en la que Geniomátic pretende apoyar, por lo que esperamos que este texto sea una herramienta útil y eficiente que aligere el trabajo con sus estudiantes. AL ESTUDIANTE: ¿Qué piensas de la Matemática? El concepto que tengas de la Matemática es muy importante para tu aprendizaje. Algunos piensan que la Matemática es un conjunto de reglas y fórmulas que hay que memorizar para el examen. Otros piensan que es un invento de muchos genios, difícil de comprender. Ambas ideas pueden perjudicar tu aprendizaje. La Matemática es lógica y sentido común. Si en una caja pones 10 manzanas y le agregas 5 más, tendrás 15 manzanas. Si manejo un carro que yendo a 100 kilómetros por hora y frena en 50 metros, el sentido común me dice que necesito unos 100 metros por adelante, para que en caso de una emergencia tenga tiempo de reaccionar y frenar con tranquilidad. En caso contrario, debo bajar la velocidad. Los conocimientos matemáticos son muy útiles para resolver problemas de cuantificación, como calcular áreas de terrenos, cantidad de materiales para construcción, estimar el tiempo de producción de un artefacto, etc. Este libro te ofrece una oportunidad para involucrarte en el maravilloso mundo de las ideas matemáticas, donde no hay límites para tu curiosidad, donde puedes explorar, imaginar, cuestionar, verificar, proponer, preguntar, responder preguntas desde tu punto de vista, compartir tus inquietudes y trabajar en equipo. En este texto encontrarás los conocimientos matemáticos siempre asociados a una aplicación práctica que te servirá de guía para que hagas lo mismo con los ejercicios de la actividad. Además, cuentas con alcances en la columna derecha, que te reforzarán, ayudarán e informarán sobre del tema principal. Los cuatro textos van acompañados por un cuaderno de trabajo que contiene ejercicios similares a los de la actividad y otros, seleccionados en tres niveles de dificultad, para que puedas practicar, reforzar y profundizar tus conocimientos. 3 3 ESTRUCTURA DEL TEXTO Sección inicial de la unidad Imagen motivadora Fotografía ilustrada que conecta una situación real con el tema de aprendizaje. Número de la unidad Título de la unidad Imagen secundaria Imagen que muestra un detalle relacionado con el tema de la lectura. Aprendizajes esperados y actividades Contienen el listado de las capacidades que desarrollarás en la unidad. Lectura motivadora Explica la relación entre la Matemática y una situación objetiva. Además formula preguntas que propician el análisis y reflexión sobre el tema. Sección central Número de capítulo Título del capítulo Recuperación de saberes previos Plantea situaciones que te servirán de base para iniciar el tema nuevo. Es algo que conoces o has tratado en los capítulos anteriores. Formalización Continúa las definiciones y conceptos de los términos matemáticos. Actividad Es un conjunto de preguntas de análisis, reflexión, de valoración, demostración, cálculo, búsqueda de relaciones, para que desarrolles, individual o colectivamente, con apoyo de tu profesor o tus compañeros. 4 3 Generación del conflicto cognitivo Es una pregunta que tendrás que responder con el desarrollo o al terminar el capítulo. Información complementaria Lecturas, notas, observación, historias, recursos tecnológicos, que contribuyen a reforzar y recrear el tema. Problemas Plantea una aplicación desarrollada del tema. Problemas Plantea una aplicación desarrollada del tema. ÍNDICE SECCIÓN INICIAL 01 ÁNGULO TRIGONOMÉTRICO Y SECTOR CIRCULAR 6 02 TRIÁNGULO RECTÁNGULO Y RAZONES TRIGONOMÉTRICAS ACTIVIDAD/EVALUACIÓN/ PROYECTO DE APRENDIZAJE SECCIÓN CENTRAL Capítulo 01: Ángulo trigonométrico 7 Actividad 01 9 Capítulo 02: Sistema de medidas angulares Sistema sexagesimal Sistema centesimal Sistema radial 10 Actividad 02 12 Capítulo 03: Conversión de unidades 13 Actividad 03 14 Capítulo 04: Longitud de un arco La circunferencia Longitud de arco 15 Actividad 04 17 Capítulo 05: Sector circular Sector circular Área de sector circular 18 Actividad 05 19 Capítulo 06: Trapecio circular Relación de áreas del sector circular 20 Actividad 06 21 Capítulo 07: Razones trigonométricas de ángulos agudos 23 Actividad 07 25 Capítulo 08: Razones trigonométricas de ángulos notables 26 Actividad 08 28 29 Capítulo 09: Propiedades de las razones trigonométricas Razones trigonométricas recíprocas Razones trigonométricas de ángulos complementarios Actividad 09 30 Capítulo 10: Solución de triángulos rectángulos 31 Actividad 10 32 Capítulo 11: Ángulos verticales 33 Actividad 11 34 Capítulo 12: Plano cartesiano La recta numérica 35 Actividad 12 36 Capítulo 13: Ángulos en posición normal Ángulos que pertenecen a algún cuadrante Ángulos cuadrantales 38 Actividad 13 40 Capítulo 14: Razones trigonométricas de ángulos de cualquier medida Razones trigonométricas en el plano cartesiano 41 Actividad 14 42 Capítulo 15: Signo de las razones trigonométricas 43 Actividad 15 44 Capítulo 16: Razones trigonométricas de ángulos coterminales y cuadrantales Razones trigonométricas de ángulos coterminales Razones trigonométricas de ángulos cuadrantales 45 Actividad 16 46 Capítulo 17: Reducción al 1er cuadrante de ángulos menores que una vuelta 47 Actividad 17 48 Capítulo 18: Reducción al 1er cuadrante de ángulos mayores que una vuelta 49 Actividad 18 51 Capítulo 19: Identidades trigonométricas pitagóricas 53 Actividad 19 54 Capítulo 20: Identidades trigonométricas recíprocas y por cociente Identidades trigonométricas recíprocas Identidades trigonométricas por cociente 55 Actividad 20 56 Capítulo 21: Identidades trigonométricas auxiliares 22 03 RAZONES TRIGONOMÉTRICAS DE ÁNGULOS DE CUALQUIER MAGNITUD 37 04 IDENTIDADES TRIGONOMÉTRICAS 57 Actividad 21 58 Capítulo 22: Razones trigonométricas de ángulos compuestos 59 seno y coseno Actividad 22 60 Capítulo 23: Tangente de la suma y diferencia de dos arcos 61 Actividad 23 62 Capítulo 24: Identidades para el arco doble 63 Actividad 24 64 52 3 5 01 Unidad ÁNGULO TRIGONOMÉTRICO Y SECTOR CIRCULAR DISEÑO DE CURVAS DE CARRETERA La sección horizontal de una curva de carretera es un trapecio circular. Los radios que limitan el trapecio son perpendiculares a la dirección de la continuación de la carretera. El diseño de una curva es parte del diseño geométrico de carreteras, una técnica de ingeniería civil que consiste en situar el trazado de una carretera o calle en el terreno. La función de las curvas es de evadir obstáculos topográficos o geológicos y adaptar las pendientes a la capacidad de desplazamiento de los vehículos. - Visita una carretera asfaltada y observa cómo está construida la curva y dibújala. http://es.scribd.com/doc/17432056/diseno-geometrico-de-carreteras APRENDIZAJES ESPERADOS Matematiza situaciones Comunica y representa • Reconoce el uso del ángulo trigonométrico y sistemas de medición angular en situaciones cotidianas. • Valora el uso de la longitud de arco, el área del sector circular y trapecio circular. 6 3 • Deduce la fórmula general de conversión angular. • Expresa ángulos en diferentes sistemas de medición angular. • Expresa con una fórmula la longitud de arco. Elabora y usa estrategias Razona y argumenta • Resuelve ejercicios y problemas sobre ángulos trigonométricos. • Aplica diversos criterios para resolver problemas de longitud de arco, área del sector circular y trapecio circular. • Propone conjeturas sobre ángulos trigonométricos y sistemas de medición angular. • Elabora conclusiones que diferencian la longitud de arco, el área del sector circular y el trapecio circular. CAPÍTULO ÁNGULO TRIGONOMÉTRICO 01 ¿Existen ángulos de 2000º? 2 Ten Presente I BIMESTRE Ángulo trigonométrico La hélice da 300 vueltas por minuto. ¿qué ángulo barre en media hora? Lad o fina l Q P P Q O 115° Se gira el rayo OP en sentido antihorario respecto al origen. + P O O O El rayo OP ha girado 115º y se ha generado el ángulo POQ de 115º. Ángulo positivo Lado inicial P T 322° El mismo rayo ha girado 322º. Si continuara girando puede generar ángulos de muchas vueltas más. El ángulo trigonométrico, a diferencia del geométrico, se genera por la rotación de un rayo respecto a su origen, desde una posición inicial hasta una posición final. O P – Ángulo negativo Q Importante: Esta definición implica: Para sumar ángulos trigonométricos, deben estar orientados en el mismo sentido. 1. El rayo tiene una posición inicial y una posición final. En su posición inicial es el lado inicial y en su posición final, el lado final. Cambio se sentido: 2. El rayo puede girar en sentido horario, entonces genera un ángulo negativo, o en sentido antihorario, entonces genera un ángulo positivo. 3. El rayo puede girar menos de una vuelta o puede girar más de una vuelta o muchas vueltas, es decir, el ángulo trigonométrico se puede extender indefinidamente, tanto positiva como negativamente. q -q Ejemplos: 1. Problema 1: Solución: En la figura mostrada, calcula el valor de en términos de . 63° –63° q – 24 24 – q 2. f f + (–) = 90º = 90º + Rpta.: 90º + 3 7 CAPÍTULO 01 ÁNGULO TRIGONOMÉTRICO Problema 2: Solución: En la figura, calcula el valor de en términos de . I BIMESTRE – + = 180º = 180º + Rpta.: 180º + Problema 3: Problema 4: En el siguiente gráfico, Determina el valor de en términos de . En la figura, calcula el valor de en términos de . 2 Operaciones con los ángulos λ Para sumar los ángulos deben tener el mismo sentido. Antes de operar se orientan todos en el mismo sentido. Solución: Solución: Ten Presente –λ a b x c – + 90º + + 90º = 360º = – 180º – = 360º + = – – 360º Rpta.: – 180º Rpta.: – – 360º –a –b x c Problema 5: Problema 6: En la figura mostrada, determina x en términos de r y f. En la figura mostrada, determina x en términos de r y f. r x f f Solución: x r Solución: -r x –f -f x r w –f + x – r = 180 x = 180° + f + r Rpta.: 180° + f + r 8 3 w – f = 90° r=w+x + r – f = 90° + x x = r – f – 90° Rpta.: r – f – 90º x=c–b–a Actividad 01 1 En la figura , calcula el valor de . 6 Determina el valor de x en la siguiente figura: 12° – 2λ 3λ +12° En la figura, calcula el valor de f. 8° – 2 f 7 De la figura, calcula . 5f + 20° 3 I BIMESTRE 2 x f – 72° 4f – 18° En la figura , calcula el valor de x. 8 En la figura , calcula x en términos de y . x 4 Determina el valor de verdad de las siguientes proposiciones. 9 5 Determina el valor de verdad de las siguientes proposiciones. 1. + = 180º .................... ( ) 2. – = 180º .................... ( ) 3. + = –180º .................... ( ) 1. + + = 270º .................... ( ) 4. – = 180º .................... ( ) 2. – + = 180º .................... ( ) 5. = .................... ( ) 3. – – = 360º .................... ( ) 4. – – = 270º .................... ( ) 5. + – = 180º .................... ( ) En la figura , calcula en términos de . λ 10 En la figura, calcula f en términos de y . f 3 9 02 CAPÍTULO SISTEMA DE MEDIDAS ANGULARES ¿Se puede inventar otro sistema aparte de los conocidos? SISTEMA SEXAGESIMAL (S) Observación 90° 120° 60° 30° 150° 1° = 0° 180° 210° 1 vuelta = 360º Ejemplo 1 Submúltiplos: Convierte 540º a radianes. 1º = 60' 1' = 60'' 330° 240° 1 vuelta 360 1° = 3600'' 540º SISTEMA CENTESIMAL (C) 140 120 g 100 g Ejemplo 2 60 g 40 g 160 g 180 g 20 g 200 g 0g 220 g 380 g 240 g 360 g 260 g 300 g 320 g 1 vuelta 1g = 400 Convierte 650g a radianes. 1 vuelta = 400g Submúltiplos: 1g = 100m 10 650g 1m = 100s 1g = 10000s p rad = 13 rad 200g 4 650g = 13 rad 4 340 g Grados sexagesimales Grados centesimales 360º 400g 9º 10g 3 Solución: Se sabe 200g = rad Equivalencia entre grados sexagesimales y grados centesimales 1 vuelta: p rad = 3 rad 180º 540° = 3 rad 80 g g 280 g Solución: Se sabe 180º = rad 300° 270° Para descubrir el valor de un ángulo de un sistema a otro, utilizamos el factor de conversión. 9° = 10g 9° 10g =1 ∨ =1 g 9° 10 "Factor de conversión" SISTEMA DE MEDIDAS ANGULARES CAPÍTULO 02 Problema 1: 2'24'' Reduce E = 1°8' + 9'' 4' Solución: E= 60' + 8' 2(60'') + 24'' 68' 144'' + = + = 17 + 16 9'' 4' 9'' 4' Convierte gesimal. Rpta.: 33 Problema 3: 180g al sistema sexa- Siendo A 180g se multiplica por el factor 31º33'21'' + 11º21'15'' = aºb'c'' 2b calcula T = a–c de conversión 9º 10g Solución: Sumando ordenadamente : Solución: 42º54'36'' = aºb'c'' 180g = 180g × 9º 10g 180g I BIMESTRE Problema 2: E = 33 a = 42; b = 54 y c = 36 = 18(9º) 2(54) 2(9)(6) Luego T = = = 18 42 – 36 42 – 36 180g = 162º Rpta.: 162º Rpta.: 18 Observación Algunas equivalencias entre los tres sistemas 360° = 400g = 2p rad SISTEMA RADIAL O CIRCULAR (R) R R R 1 radián R 180° = 200g = p rad 90° = 100g = p rad 2 Si se establece que el ángulo de una vuelta mida 2p radianes, entonces la unidad es un radián, que es la medida de un ángulo central que subtiende un arco de igual longitud que el radio. Medidas angulares (en radianes) de algunos ángulos notables 45° = 50g = p rad 4 36° = 40g = p rad 5 18° = 20g = p rad 10 9° = 10g = p rad 20 Como el ángulo de una vuelta mide 2p radianes, la media vuelta mide p radianes, el cuadrante mide p/2 radianes y el octante, p/4. O Equivalencias entre los tres sistemas 360º = 400g = 2p rad 180º = 200g = p rad 3 11 CAPÍTULO 02 SISTEMAS DE MEDIDAS ANGULARES Problema 4: Convierte 11 rad al sistema 5 sexagesimal. Problema 5: Reduce E = 5 rad – 515º + 350g 250g – 365º + 3 rad I BIMESTRE Se sabe rad = 180º 10g = 9º, se expresa en un solo sistema : Se sabe rad = 180º 180° 11 rad = 396º p rad 5 11 rad = 396º 5 Rpta.: 396º E= E= 300g + 900° + 7rad 1200° – 800g + 3rad Solución: H= 30(9°) + 900° + 7(180°) 1200° – 80(9°) + 3(180°) 5( rad) – 515º + 35(10g) 25(10g) – 365º + 3( rad) 5(180º) – 515º + 35(9º) 25(9º) – 365º + 3(180º) = 7 4 Rpta.: 7 4 Problema 7: Simplifica E= Solución: Solución: Problema 6: H= 270 + 900 + 1260 1200 – 720 + 540 H= 41 17 Rpta.: 41 17 Solución: De la figura, calcula n. 2p rad + [–2 (1 – 2n)°] = 90° n 360° – 2(1 – 2n)° = 90° n 2p rad n 2p rad n 2(1 – 2n)° ⇒ n2 – 23n + 90° = 0 n = 5 –2(1 – 2n)° ∨ n = 18 Rpta.: 5 ; 18 Actividad 02 1 Calcula P = 6º40' + 8'20'' . 50' 10'' 6 Convierte 280º a radianes. 2 g m m s Calcula H = 8 60 + 12 80 . 20m 40s 7 Convierte 325g a radianes. 3 Convierte 243º al sistema centesimal. 8 Convierte 22 rad a unidades sexagesimales. 5 4 Convierte 450g al sistema sexagesimal. 9 Convierte 28 rad a unidades centesimales. 5 5 Calcula el valor de la expresión R= 12 1g + 1m + 1s . 1'' 1º 1' 3 10 Reduce P= 2 rad – 195º + 150g 42º – 80g + rad CAPÍTULO CONVERSIÓN DE UNIDADES ¿Cuánto vale x? Un ángulo mide S° y Cg. ¿Cuál es mayor S o C? 80g 100° 03 I BIMESTRE 13p rad 20 x° En grados sexagesimales En grados centesimales En radianes 40g 36° 36° 40g rad En el sistema sexagesimal En el sistema centesimal En el sistema radial Estos ángulos son congruentes, pero los números que indican sus medidas son distintos porque corresponden a diferentes sistemas. p/5 1 36° = = = 180° 200g 5 p 40g En general: S° Cg R rad En el sistema sexagesimal En el sistema centesimal En el sistema radial 2 Ten Presente Algunos valores aproximados de p • p ≈ 22 7 • p≈ 2+ 3 • p ≈ 10 • p ≈ 3,14 R S C = = 180 200 p Por factor de conversión Dado que 180º = 200g 9° 10g = =1 10g 9° Unidad que no quiero Supongamos que queremos convertir 153º en grados centesimales, entonces, el grado centesimal es la unidad que queremos y el grado sexagesimal, la que no queremos, de 10g modo que el factor de conversión es: 9° Convierte 117º al sistema centesimal. Solución: C S Se sabe = 10 9 10g 9° Factor de conversión: Este cociente se denomina factor de conversión y como su valor es uno se puede multiplicar a cualquier número sin cambiarle de valor. Problema 1: Observación Unidad que quiero 17 153° = 153°× 10g = 170g 9° 1 S C R = = =k 9 10 p 20 C = 10k R= pk 20 S = # de grados sexagesimales C = # de grados centesimales \ 153° = 170g R = # de radianes C 117 Reemplazando = 10 9 C = 130 117º = 130g S = 9k p = 3,141592... ≈ 3,1416 Rpta.: 130g 3 13 CAPÍTULO 03 CONVERSIÓN DE UNIDADES Problema 2: Problema 4: Convierte 108º a radianes. Siendo S, C y R los números convencionales para un mismo ángulo, I BIMESTRE Solución: S R Se sabe = 180 Reemplazando 108º = reduce R 108 3 = R= 180 5 3 rad 5 Rpta.: 3 rad 5 2 3S – 2C – 40R Se sabe S = 180K; C = 200K y R = K Reemplazando: T= T= S = 180K; C = 200K y R = K H= 3C + 4S – 20R Solución: Problema 3: Siendo S, C y R los números convencionales para un mismo ángulo, reduce H = C – S . 10R Solución: C R S Se sabe = = =K 180 200 Reemplazando H = T= 200K – 180K 2 = 10K 3(200K) + 4(180K) – 20(K) 3(180K) – 2(200K) – 40(K) 600 + 720 – 20 540 – 400 – 40 T = 13 Rpta.: 13 Rpta.: 2/ Actividad 03 1 Convierte 126º al sistema centesimal. 2 Convierte 225º a radianes. 3 La suma de los números de grados sexagesimal y centesimal para un mismo ángulo es 76, calcula el número de grados sexagesimales que posee dicho ángulo. 4 5 14 Siendo S, C y R los numeros convencionales para un mismo ángulo, reduce E = 3C – 2S . 40R La semidiferencia de los números de grados centesimal y sexagesimal para un mismo ángulo es 4, calcula el número de grados centesimal que posee dicho ángulo. 3 6 Siendo S, C y R los numeros convencionales para un mismo ángulo, reduce P = S + C + 120R . 2C – S – 20R 7 Determina la medida circular de un ángulo cuyo número de grados sexagesimal y centesimal cumplen 3S – 2C = 35. 8 Determina la medida circular de un ángulo cuyo número de grados centesimales excede al número de grados sexagesimales en 16. 9 Siendo S y C los números convencionales para un mismo ángulo, reduce H = C+S + C–S 4S . C–S 10 Determina la medida circular de un ángulo cuyo número de grados sexagesimales y centesimales cumplen S = 5n + 1 y C = 6n – 2. CAPÍTULO LONGITUD DE ARCO 04 60 ¿Cualquier curva es un arco? cm 60 cm I BIMESTRE 2p rad 3 La circunferencia R Centro R Radio A B La circunferencia es el conjunto de puntos del plano que equidistan de un punto llamado centro. A la distancia del centro a los puntos de la circunferencia se le denomina radio, cuya longitud generalmente se designa con R. Longitud de arco Observación L 24 m Al dividir la longitud de cualquier circunferencia entre la longitud de su diámetro siempre resulta p: Se deduce que para calcular la longitud de la circunferencia hay que multiplicar el radio por el ángulo de una vuelta, en radianes (2p). L R R L R 75º 24 m En esta figura el ángulo central está en grados sexagesimales. Para calcular la longitud de arco, pasamos la medida del ángulo central de grados a radianes: 5 L = p L = 2pR 2R • 75° = 75° × prad = 5p rad ángulo de una vuelta L= p R 3 Por consiguiente, para calcular la longitud de cualquier arco de circunferencia, hay que multiplicar el radio por el ángulo central, en radianes. L = qR R L q rad R q= L R R=L q 12 12 • L = qr L = 5p (24) 12 L = 10p m En general: 180° L: Longitud del arco q: Medida del ángulo central, en radianes R: Radio de la circunferencia Se denomina arco de circunferencia a un fragmento de la circunferencia cuya extensión se denomina longitud de arco y se mide en unidades de longitud. 3 15 CAPÍTULO 04 LONGITUD DE ARCO Problema 1: Problema 2: Calcula la longitud de un arco correspondiente a un ángulo central de 54º en un circunferencia cuyo radio mide 30 cm. En la figura mostrada, calcula . 6 cm Solución: I BIMESTRE B p rad Ángulo central: = 54º 180° ⇒= Radio: R = 30 cm 0 A 3 rad 10 Solución: Se sabe L = R Longitud de arco: Reemplazando 4 cm = (6 cm) 3 ×(30) = 9 cm 10 L = 9 cm L = R = = 2 rad 3 Rpta.: 2 rad 3 Rpta.: 9 cm Problema 3: Problema 4: Calcula la longitud de un arco correspondiente a un ángulo central de 80g en una circunferencia cuyo radio mide 20 cm. En la figura calcula . Solución: Ángulo central = 80g 4b cm p rad 200g 0 2 = rad 5 Radio: R = 20 cm B b cm A Solución: Longitud de arco: Se sabe L = R 2 L = R = ×(20) = 8 cm 5 L = 8 cm Reemplazando: 4b cm = (b cm) = 4 rad Rpta.: 4 rad Rpta.: 8 cm Problema 5: En la figura, r = 90 cm. Solución: Calcula la longitud del arco BC. B 1,6 A AB = 4(36) 74° 37° A 90 O 90 C 5(36) r r O 16 B AB = (90) 10 ) 6 L 4(3 37° C ABC: notable de 37° y 53° ⇒ mBA = 37° Longitud de arco: L = 74° p (90) 180° L = 37p cm Rpta.: 37 cm 16 3 Actividad 04 Calcula la longitud de un arco correspondiente a un ángulo central de 72º en una circunferencia cuyo radio mide 10 cm. 2 Calcula la longitud de un arco correspondiente a un ángulo central de 140g en una circunferencia cuyo radio mide 60 cm. 3 7 La longitud de un arco ubicado en una circunferencia es de 60 cm. Si el radio se incrementa en el triple y el ángulo central se reduce a la mitad, se genera un nuevo arco cuya longitud es: 8 En la figura, calcula H = En la figura, calcula la longitud del arco EF. b b 2b cm F b 3f E 2f O b A O 4 5 b f B L 9 F P 2a D L3 H 3a b b b M E F O L2 L3 b A En la figura, calcula . a b L1 + 2L2 . 3L3 B L2 L1 La longitud de un arco correspondiente a un ángulo central de 144º en una circunferencia de radio R es 24 cm. Calcula R. En la figura, calcula T = N L1 + L2 . L3 I BIMESTRE 1 B b 2a E a b A B a E C F a O 2a L1 10 En la figura, calcula . F A 4a 6 6 H En la figura, calcula E = L1 + L2 . L3 a M O L1 a P 6 E P H L3 A O L2 T B 3 17 CAPÍTULO 05 SECTOR CIRCULAR I BIMESTRE ¿El área de un sector circular es proporcional al radio o al cuadrado del radio? Observación ¿Qué área tiene esta concha de abanico? 12 120° cm 12 cm Sector circular Área del sector circular A R R R AOB: Es un sector circular Se llama sector circular a la región circular limitada por dos radios y el arco correspondiente. 45º R S = bh 2 B Haciendo analogía, si aplicamos la fórmula del área del triángulo al sector circular tenemos: S= = S LR 2 LR θ × 2 θ Problema 1 Calcula el área de un sector circular cuyo ángulo central mide 60º y su radio 12 cm. Problema 2 Solución: Solución: S= (θR)R 2 S= θR 2 2 L2 q en ⇒ S= 2θ radianes Calcula el área de un sector circular cuya longitud de su arco es 16cm y su radio mide 8 cm. En esta figura el ángulo central está en grados sexagesimales. Para calcular su área tenemos dos opciones: 1. Pasar el ángulo central de grados a radianes y aplicar una de las fórmulas del área del sector circular. 2. Aplicar una regla de tres, con el siguiente criterio: cuando el ángulo central es 360º (1 vuelta) el área es pR2, entonces, ¿qué área corresponde a un ángulo central de a grados?: Ángulo central Área 360º pR2 aº S 2 S = a°pR 360° S 8 cm S Para a = 45º y R = 32 m: 2 S = 45°p(32) = 128p 360° 12 cm Se sabe S = 1 R2 2 60° p S= 1 ×(12)2 = 24 cm2 2 180° S = 24 cm2 Rpta.: 24 cm2 18 32 m b S B 60º h R L q O A L 32 m 3 Se sabe S = 1 LR 2 1 S = (16)(8) = 64 cm2 2 S = 64 cm2 Rpta.: 64 cm2 S = 128p m2 SECTOR CIRCULAR Problema 3 Calcula el área de un sector circular cuya longitud de su arco es 24 cm y su ángulo central correspondiente mide 120º. Solución: Se sabe S = 1 2 S 120º 2 S = 1 (24p) = 432 cm2 2 2p 3 Obs: 120° = 2p 3 Rpta.: 432 cm2 b De la figura, E calcula S + S2 H= 1 . S1 – S 2 S1 S2 f f O b F A 2b Solución: Se sabe S = 1 R2 2 H= S = 432 cm2 B Problema 4 I BIMESTRE L2 CAPÍTULO 05 1 (2f)(2b)2 + 1 (3f)(b)2 2 2 = 1 (2f)(2b)2 – 1 (3f)(b)2 2 2 8+3 11 = 8–3 5 H = 11 5 Rpta.: 11 5 Actividad 05 1 2 Calcula el área de un sector circular cuyo ángulo central mide 150º y la longitud de su radio es 6 cm. Calcula el área de un sector circular cuya longitud de su arco es 6 cm y su ángulo central correspondiente mide 135º. 4 De la figura, calcula P = P b S3 E 6 7 8 6 El área de un sector circular es 60 cm2. Si duplicamos el radio y reducimos el ángulo central en su mitad, se genera un nuevo sector circular cuya área es : En la figura, calcula 2S1 + 3S2 . S 1 – S2 3b 5f O 4b B El área de un sector circular es 120 cm2 y la longitud de su arco correspondiente es 48 cm. Calcula la longitud del radio de dicho sector. En la figura, calcula E = 9 3b S2 5b S1 30º 45º S1 S2 S1 54º 36º T= 3f A b F S 1 + S3 . S 1 – S2 S2 4 Calcula el área de un sector circular cuya longitud de su arco es 24 cm y su radio mide 10 cm. 3 5 2 8b El área de un sector circular es 36 u2. Si duplicamos el ángulo central y el radio se triplica, se genera un nuevo sector circular cuya área es : 10 De la figura, calcula x. 2 S1 + S2 . S 1 – S2 O E x D 2 f F 9S S 2 A 2 B 3 x C 19 CAPÍTULO 06 TRAPECIO CIRCULAR ¿Qué tiene en común el trapecio circular y el trapecio poligonal? I BIMESTRE 125304 Matemática en la vida Diseño de una curva Queremos diseñar la curva de este tramo de la carretera. R1 O R2 (L1 + L2 )m 2 S= θ(R12 − R2 2 ) 2 L1 S L2 S= m Trapecio circular es la región limitada por dos arcos de dos circunferencias concéntricas y dos radios. S= 1. Trazamos la bisectriz del ángulo que forman los dos tramos y elegimos el radio de curvatura. L12 − L2 2 2θ Relación de áreas del sector circular m M m O m mP m A m R 3L 2L 5S S L 3S 7S N m Q m S m F Problema 1 Calcula el área del trapecio B circular. b O b 4L B Radio Área MON m S POQ 2m 4S ROS 3m 9S AOB 4m 16S Obsérvese que el área del sector circular es proporcional al ángulo central y al cuadrado del radio. Problema 2 Calcula el área del trapecio circular. S A Solución: 8 cm E Reemplazando: (6 + 2) S= ×(8) = 32 cm2 2 S = 32 cm2 Rpta.: 32 cm2 3 2. Con el radio elegido trazamos curvas de circunferencia tangentes a los bordes de la carretera. D 2 cm B S 3 cm O (L + L2) Se sabe S = 1 ×d 2 20 Sector 60° 3 cm A 2 cm C Solución: Se sabe S = 1 (R12 – R22) 2 Reemplazando: 8 S = 1 (52 – 32) = cm2 2 3 3 S= 8 cm2 3 Rpta.: 8 cm2 3 Obsérvese que cuanto menor es el radio de curvatura la curva es más cerrada. El tramo de la curva es un trapecio circular. TRAPECIO CIRCULAR Problema 3 Calcula el área del trapecio circular. CAPÍTULO 06 Solución: Se sabe S = T (L12 – L22) 2 Reemplazando: N SS 45° M (3)2 – (2)2 2 4 = 10 cm2 I BIMESTRE O S= S = 10 cm2 P Rpta.: 10 cm2 Actividad 06 1 2 3 Calcula el área de un trapecio circular cuyas longitudes de sus arcos son 2 cm y cm, y sus radios miden 3 cm y 6 cm respectivamente. Calcula el área del trapecio circular. 7 D S1 O En la figura, calcula H = S 1 + S2 . S3 S2 O 2a C 72° 2 cm 5 cm F b E b D S2 b S A B O C S1 3 60° calcula t. 8 Calcula el área de un trapecio circular cuyas longitudes de sus arcos son L1 y L2, y sus radios miden R y r respectivamente (R > r). 9 Calcula el área D a de un trapecio circular en términos de a y b. b A b B b C 12S B t D 2 F S 2 A t C 2 E 2 O C A 4 cm B S b 2a O En la figura, A a E D En la figura, calcula circular. S O 2a el área del trapecio 2 cm 5 cm 5 F a B En la figura, calcula E = S1 + 2S2 . S1 – S 2 Calcula el área de un trapecio circular cuyas longitudes de sus arcos son 2 cm y 3 cm, y su ángulo central correspondiente mide 36º. B 4 6 2a 10 Calcula el área del trapecio circular AEFB. A a C F B 2 O 60° A E 3 21 02 Unidad TRIÁNGULO RECTÁNGULO Y RAZONES TRIGONOMÉTRICAS EL PLANO INCLINADO El plano inclinado es una superficie plana que forma con otra un ángulo muy agudo. Comúnmente se aprecia como rampa, la cual aumenta la distancia de la carga que se debe mover, disminuyendo de ese modo la fuerza necesaria para elevarla. Sus principales aplicaciones son tres: Como rampa (carreteras, acceso a garajes subterráneos, escaleras...), como hélice para convertir un movimiento giratorio en lineal (tornillo de Arquímedes, tornillo, sinfín, hélice de barco) y como cuña (cuchillo, tijera, sierra, hacha, arado, formón, abrelatas, ...) - Averigua qué pendiente tienen en promedio las escaleras de las casas. http://concurso.cnice.mec.es/cnice2006/material107/operadores/ope_planoinclinado.htm APRENDIZAJES ESPERADOS Matematiza situaciones Comunica y representa Elabora y usa estrategias Razona y argumenta • Identifica los elementos de un triángulo rectángulo y establece las razones trigonométricas de sus ángulos agudos. • Valora la utilidad de las propiedades de las razones trigonométricas. • Expresa en forma simbólica las razones trigonométricas de un ángulo agudo en un triángulo rectángulo. • Expresa mediante tablas las razones trigonométricas de ángulos notables. • Resuelve triángulos rectángulos utilizando las R.T. de ángulos agudos y ángulos notables. • Elabora diversas estrategias para resolver problemas que involucran a las propiedades de las R.T. • Justifica el uso las propiedades de las razones trigonométricas. • Establece relaciones entre las razones trigonométricas de un ángulo agudo en un triángulo rectángulo. 22 3 ¿Cuál es la altura de la torre? 45 07 ¿Cuándo un cateto es adyacente a un ángulo? h 22° CAPÍTULO RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS m La Collpa - Cajamarca 6 22° 5 4 2 10 2 4 5 = = = 0,4 5 10 15 Nota • Notación de lados y ángulos del triángulo rectángulo. B Esta relación nos permitirá calcular la altura de la torre, puesto que: c h = 0,4 h = 45×0,4 = 18 m 45 15 A Si en lugar de 22º el ángulo fuera de 50º la relación de catetos valdría 1,19. Así para cada ángulo hay un valor. No solamente la relación de catetos es constante para cada ángulo, sino, la relación entre cualquier par de lados. Con los lados del triángulo rectángulo se puede establecer seis relaciones en total y por la importancia que tienen a cada uno se le ha dado un nombre. Estas son las razones trigonométricas (R.T.). a C b Los vértices se denotan con letras mayúsculas y la medida de los lados con las letras del vértice opuesto pero en minúsculas. • El cateto es opuesto o adyacente según el ángulo al que se hace referencia. Seno senA = Cateto opuesto a A Hipotenusa Coseno cosA = Cateto adyacente a A Hipotenusa Tangente tanA = Cotangente cotA = Cateto adyacente a A Cateto opuesto a A BC: Secante secA = Hipotenusa Cateto adyacente a A AC: Cosecante cscA = Hipotenusa Cateto opuesto a A Cateto opuesto aA Hi po ten B c A A Cateto adyacente a A ten us Cateto opuesto a B Cateto adyacente a A po Cateto opuesto a A Cateto adyacente a B C B C a b a Hi Cateto opuesto a A Cateto adyacente a A us a B A Cateto opuesto a B Cateto adyacente aB C AB: Hipotenusa 3 23 II BIMESTRE En la figura se observa que mientras el ángulo se mantiene en 22º los catetos de los triángulos están en la relación de 2 a 5: CAPÍTULO 07 RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS Problema 1: En la figura, calcula la altura de la Chullpa, si tan35º = 0,7. Solución: h 10 • tan35° = 0,7 = II BIMESTRE 10 m 35° h 10 h h=7 10 35° Rpta.: 7 m Problema 2: en un triángulo rectángulo recto en C, tanA = 5/12. Calcula las demás razones trigonométricas del ángulo A. • c2 = 122 + 52 = 169 c = 13 • cotA = 12 5 • cosA = 12 13 Solución: • cscA = 13 5 • senA = 5 13 B c A 5 • secA = 13 12 C 12 Recuerda Teorema de Pitágoras B En un triángulo rectángulo ABC, recto en C, calcula sen2A + sen2B. a2 a = b b2 • sen2B = 2 c2 c = 2 b b Solución: b A c 2 • sen2A = • sen2A + sen2B = a sen2A + sen2B = C sen2A + sen2B = 1 Problema 4: Solución: En un triángulo rectángulo recto en C, tanA + tanB = 8. Calcula E = secAsecB. • tanA = B c A 24 a b c2 a2 + c2 a2 + = 2 2 b b2 b B C 3 a b b2 =1 b2 • tanB = c a C Problema 3: c2 = a2 + b2 Rpta.: 1 b a a b a2 + b2 + = =8 b a ab c c a2 + b2 E= × = =8 b a ab Rpta.: 8 b A RAZONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS CAPÍTULO 07 Problema 5: Problema 6: En un triángulo rectángulo ABC, recto en B, se cumple: 4senAsenC = 1. En la figura, calcula: C + 2 secA + tanA. n Calcula tanA + tanC. Solución: A C Teorema de Pitágoras: Solución: b a b2 Teorema de Pitágoras: A c = a2 + c2 n–2 n B (n + 2)2 = n2 + (n – 2)2 n2 + 4n + 4 = n2 + n2 – 4n + 4 B 4senAsenC = 1 ⇒ 4 a c · b b tanA + tanC = a c + = c a tanA + tanC = 4ac =4 ac a2 + ac 8n = n2 ⇒ b2 = 4ac c2 = n=8 b2 ac 8+2 8 + 8–2 8–2 Luego: secA + tanA = secA + tanA = 3 Actividad 07 1 2 3 En un triángulo rectángulo, las longitudes de sus catetos son 2 y 3. Calcula la secante del menor de los ángulos agudos. 6 En un triángulo rectángulo ABC, recto en B, AB = c, BC = a y AC = b, Calcula R= Las longitudes de los catetos de un triángulo rectángulo son 3 y 5. Calcula la diferencia de los cuadrados del seno con el coseno del mayor ángulo agudo. En un triángulo rectángulo el seno del menor de sus ángulos agudos es 0,2. Calcula la tangente del mayor de sus ángulos agudos. (2c cscA + b tanC) cosC c 7 En un triángulo rectángulo las longitudes de los lados mayores son 12 y 8. Calcula la tangente del menor de los ángulos agudos. 8 En un triángulo rectángulo ABC, recto en B, AB = c, BC = a y AC = b. Calcula H= 4 En la figura, calcula tanf + tan. 2 m⋅n f 5 n m En un triángulo rectángulo, las longitudes de los lados menores son 3 y 7. Calcula la suma de senos de los ángulos agudos. 9 bcosA + atanC c En un triángulo rectángulo las longitudes de los lados menores son 12 y 35. Calcula la diferencia entre la secante y tangente del menor de los ángulos agudos. 10 En la figura, calcula sec + csc. b+5 b+4 b–3 3 25 II BIMESTRE Rpta.: 3 Rpta.: 4 08 CAPÍTULO RAZONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES ¿Cuál es mayor, sen30º o cos30º? 3m 30° 2m Los ángulos notables están asociados a los triángulos rectángulos. Dado que las razones trigonométricas no dependen de la longitud de los lados del triángulo, sino, sólo de los ángulos, vamos a tomar los triángulos notables con medidas convenientes de sus lados con las cuales calculamos las razones trigonométricas de sus ángulos. Triángulo notable de 15º y 75º 75° 4 6– 2 15° R.T. de 30° y 60° R.T. de 45° ° 2 2 3 53° 2 1 60° Nota 5 3 37° 45° 1 1 1 4 30° 60° 45° 37° 53° 1 2 3 2 2 2 3 5 4 5 Coseno 3 2 1 2 2 2 4 5 3 5 Tangente 3 3 3 1 3 4 4 3 Cotangente 3 3 3 1 4 3 3 4 Secante 2 3 3 2 2 5 4 5 3 2 2 3 3 2 5 3 5 4 Seno Cosecante 26 3 6+ 2 R.T. de 37° y 53° 45° 30 II BIMESTRE Datos Los ángulos agudos del triángulo rectángulo de 3; 4 y 5 son aproximados. Las medidas exactas de los ángulos son: 36º 52' 11,6" y 53º 7' 48,4" 53°7’48,4’’ 5 3 36°52’11,6’’ 4 RAZONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES CAPÍTULO 08 Problema 1: 2 2 Calcula H = tan 30º + tan45º + tan 60º. cot45º cot30º Solución: Reemplazando valores: H = H= 2 3 +1+( 3 )2 3 (1)( 3 ) 1 +1+3 3 = 3 13 3 9 Rpta.: 13 3 9 Problema 2: Calcula H = sen37º + cos37º . tan60º + tan45º Historia Solución: Reemplazando valores: 3 +1 = 7( 3 – 1) 7 = 5( 3 + 1) 5( 3 + 1)( 3 – 1) 7( 3 – 1) 10 Rpta.: Problema 3: 7( 3 – 1) 10 Solución: C En la figura calcula cot. 60° C 150° B 6 A 150° f A 8 30° 4 3 B 6 AHC: cot = 6+4 3 4 cot = 3+2 3 2 Problema 4: Solución: En la figura, AM es mediana. Calcula tanr. A A 4 8 Rpta.: B M C b M b 2b tanr = 2b B 3+2 3 2 ABH: tanr = 45° H 45° b El astrónomo y matemático hindú Aria Bhatta (476–550 d. C.) estudió el concepto de «seno» con el nombre de ardhá-jya, siendo ardhá: ‘mitad, medio’, y jya: ‘cuerda’). Cuando los escritores árabes tradujeron estas obras científicas al árabe, se referían a este término sánscrito como jiba . Sin embargo, en el árabe escrito se omiten las vocales, por lo que el término quedó abreviado jb. Escritores posteriores que no sabían el origen extranjero de la palabra creyeron que jb era la abreviatura de jiab (que quiere decir ‘bahía’). 1 2 C Rpta.: 1/2 3 27 II BIMESTRE 3 + 4 5 5 T = T= Origen de la palabra seno CAPÍTULO 08 RAZONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES Problema 5: Problema 6: En la figura, calcula cotf + cscf. 3tan p + 5sen60° 6 Si senf = 7 cot30° + 5 tan p 2 3 3 20 Solución: B 37° f 51 Calcula: R = 7(cscq – cotq). (q <90°) Solución: a 20 12 Teorema de Pitágoras: f 37° a2 = 122 + 352 16 A H 35 C 51 ⇒ a = 37 senq = 7( 3) + 5( 3) 2 3 ⇒ senq = 21 29 n2 + 212 = 292 ⇒ n = 20 29 21 ⇒ R = 7 29 – 20 21 21 35 37 72 cotf + cscf = + = 12 12 12 cotf + cscf = 6 Rpta.: 6 II BIMESTRE 3 3+5 3 3 2 R=3 q n Rpta.: 3 Actividad 08 1 E= 2 6 Calcula la expresión sen30º + sen37º + tan45º cos30º + cos37º + cot45º En la figura calcula tan. P En un triángulo rectángulo ABC, recto en B, se traza la mediana CM; tal que mBMCB = y mBMAC = 37º. Calcula tan + cot. 7 En un triángulo ABC, mBBAC = 53º mBBCA = , AB = 10 y BC = 17. Calcula cot + csc. 12 120° Q 3 R 10 En un triángulo rectángulo ABC, recto en B, se traza la mediana AM; tal que mBMCA = 53º y mBMAC = . Calcula csc. 9 Calcula Calcula la expresión H= tan60º + tan45º + tan37º cot60º + cot45º + cot37º M = tan 4 En el lado BC de un cuadrado ABCD se ubica un punto T, tal que mBTDC = 37º. Calcula la tangente del ángulo TAB. 5 En la figura calcula sec. B 5 6 30° A 28 8 3 C 37° 53° 45° + tan + tan . 2 2 2 10 En los lados BC y CD de un cuadrado ABCD se ubican los puntos P y T respectivamente, tal que mBTAD = 37º y mBATP = 90º. Calcula la tangente del ángulo PAB. Si senA = cosB, ¿cuánto mide el ángulo C? Observación B Razones trigonométricas recíprocas Razones trigonométricas recíprocas Recíprocos C A a c B senA = a b cscA = b a senA cscA = 1 senA = 1 cscA cosA = c b secA = b c cosA secA = 1 cosA = tanA = a c 1 secA cotA = c a tanA cotA = 1 tanA = 1 cotA Problema 1: Problema 2: Si sen(3x – 10º) csc(70º – 2x) = 1. Si tan( + 24º) cot(2 + 9º) = 1, Calcula sen2(x – 1°). calcula cot3f. Solución: Solución: R.T. Reciprocas: R.T. Reciprocas: sen(3x – 10º) csc(70º – 2x) = 1 tan( + 24º) cot(2 + 9°) = 1 3x – 10º = 70º – 2x + 24º = 2 + 9° = 15º 5x = 80º x = 16º • sen35°csc35° = 1 • tan(3x + 20º) cot(30º + 2x) = 1 3x + 20º = 30º + 2x x = 10º cot3 = cot45º sen2(x – 1º) = sen30º Observación cot3 = 1 1 sen2(x – 1º) = 2 Rpta.: 1 Rpta.: 1/2 sen = cos(90° – ) Razones trigonométricas de ángulos complementarios Iguales B a b 1 sec40° Luego: cot3 = cot3(15º) Luego: sen2(x – 1º) = sen2(16º – 1º) c • cos40° = II BIMESTRE b 09 ¿Al coseno de qué ángulo es igual el seno de 30º? C A A CAPÍTULO PROPIEDADES DE LAS RAZONES TRIGONOMÉTRICAS C senA = a c cosB = a c senA = cosB tanA = a b cotB = a b tanA = cotB secA = c a cscB = c a secA = cscB tan = cot(90° – ) sec = csc(90° – ) • tan42° = cot48° • sec25° = csc65° • sec(x + 21º) = csc(15º + 2x) (x + 21º) + (15° + 2x) = 90º 3 29 CAPÍTULO 09 PROPIEDADES DE LAS RAZONES TRIGONOMÉTRICAS Problema 3: Problema 4: Si sen5x = cos(x + 18º), calcula tan3(x – 2°). Reduce H = tan20º tan30º tan40º tan50º tan60º tan70º sen10º tan10º sec80º tan80º Solución: sen5x = cos(x + 18º) Solución: 5x + x + 18º = 90º x = 12° Aplicando razones de Bs complementarios. Luego: tan3(x – 2º) = tan3(12º – 2º) H= tan3(x – 2º) = tan30º tan3(x –2º) = 3 3 3 Rpta.: 3 tan20º tan30º tan40º cot40º cot30º cot20º sen10º tan10º csc10° cot10º Ordenando por recíprocas: H= II BIMESTRE H= tan20º cot20º tan40º cot40º tan30º cot30º sen10º csc10º tan10 cot10º 1(1)(1) =1 1(1) Rpta.: 1 Actividad 09 1 Si sen(2 + 5º) csc(50º – ) = 1, 7 calcula el valor de . calcula sen2 + cos3. 2 Si tan(3x + 8º) = cot(2x – 8º), Si tan(3 + 4º) tan(26º + 2) = 1, 8 Si cos6 = sen4, calcula calcula sen(x + 12º) + cos(3x + 6º). T= 3 tan(5 + ) + sec(3 + 2) cot(5 – ) + csc( + 4) Reduce P= sen20º sen30º sen40º sec50º sec60º sec70º tan36º sen54º tan54º sec36º 9 Si tan3x = cot5x, calcula P= 4 Si cos(7 – 11º) sec(2 + 59º) = 1, calcula tan2( + 1º) + cot( + 16º). 5 Si sen(6 + 5º) = cos( – 20º), calcula tan3 + tan4. 6 sen7x cos2x + cosx sen6x Calcula la expresión: R = (8cot10º + 6tan80º) tan10º 30 3 10 Calcula la expresión: H= sen1º + sen2º + sen3º + ... + sen89º cos1º + cos2º + cos3º + ... + cos89º Calcula la altura de la torre en término de d y f. CAPÍTULO SOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS 10 ¿Se puede resolver un triángulo rectángulo conociendo solamente los ángulos agudos? f d Resolver un triángulo rectángulo es determinar la longitud de cada lado y la medida de cada ángulo. 1. c x = cosf y c x = c cosf y = senf c y = c senf x 2. Método práctico de solución de triángulos rectángulos Conociendo la medida de un ángulo agudo y la longitud del cateto adyacente (f, a) z y = tanf y a y = a tanf z = secf a z = a secf a 3. c b x x = cotf b x = b cotf z = cscf b z = b cscf Problema 1: a A H C 18 30° Para ello buscaremos una R.T. de 30º que relacione el lado conocido con el desconocido. Puede ser sen30º o csc30º. Elegimos la razón en la que x está como numerador. En general, en forma práctica: Lo que quiero Razón = Lo que tengo trigonométrica (q) • x = csc 30° 18 x = 2 x = 36 18 x B A b B En la figura, calcula AB en términos de l y . x En este triángulo queremos calcular x. Conociendo la medida de un ángulo agudo y la longitud del cateto opuesto (f, b) z Observación H C ABC: x = lcos Rpta.: lcos 3 31 II BIMESTRE Conociendo la longitud de la hipotenusa y la medida de un ángulo agudo (c, f) CAPÍTULO 10 SOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS En la figura, calcula BC en términos de n y . x C B T A Historia Origen de la palabra tangente y cotangente C Problema 3: N En la figura, calcula BN en términos de t y . C N B A ANB: x = ttanq B A El nombre tangente fue usado por primera vez por Thomas Pinche en 1583 y el término cotangente fue usado por primera vez por Edmund Gunter en 1620. x t t II BIMESTRE D n T Luego: x = nsen + n x = n(sen + 1) Rpta.: n(sen + 1) D n C n n A x B Problema 2: Rpta.: ttanq Actividad 10 1 En la figura, calcula AB en términos de a; b; y b. P a A q C b 2 En un triángulo rectángulo ABC, recto en B, AB = n y mBC = . Calcula el perímetro de la región ABC. 3 En la figura, calcula BC en términos de b; y . b A C B B D A 7 En un triángulo rectángulo, uno de sus ángulos agudos mide y la longitud de su hipotenusa es t. Calcula el área de la región limitada por dicho triángulo. 8 En la figura, ABCD es un rectángulo. Calcula TC en términos de b y . D C B B 4 5 32 2b C En un triángulo rectángulo ABC, recto en B, AC – BC = l y mBA = . Calcula AB en términos de l y . En un triángulo acutángulo ABC, mBA = y mBC = . Calcula 6 T 5b AB en términos de y . BC En la figura, ABCD es un cuadrado. Calcula PB en términos de q y w. 3 A 9 P D En el triángulo rectángulo ABC, recto en B, se traza la altura BH; tal que HA = a y mBHAB = . Calcula HC en términos de a y . 10 En el triángulo rectángulo ABC, recto en B, se traza la altura BH; tal que HA = h y mBHBA = . Calcula AC en términos de h y . CAPÍTULO 11 ÁNGULOS VERTICALES Calcula la altura del volcán en términos de q y d. ¿Cuánto puede medir a lo más un ángulo de depresión? q d Cuando se observa un punto que está por encima o por debajo del nivel de la vista, la línea imaginaria que se dirige de la vista al punto se llama línea visual. Si es hacia arriba, el ángulo que forma la línea visual con la horizontal se denomina ángulo de elevación. Si es hacia abajo, el ángulo que forma la línea visual con la horizontal se denomina ángulo de depresión. f ea l a isu v ea Lín Lín vis Ten Presente Ángulo de observación ua l q q Línea horizontal q: Ángulo de elevación. f: Ángulo de depresión. La línea horizontal con la visual determinan un plano vertical, en el que están contenidos los ángulos de elevación y de depresión, razón por la cual se denominan ángulos verticales. Problema 1: Problema 2: Desde el punto del suelo se observa la parte más alta de un poste con un ángulo de elevación de 53º. Si dicho punto se encuentra a 48 m de la base del poste. ¿Cuál es la altura del poste? Desde lo alto de un edificio de 240 m de altura se observa un punto en el suelo con ángulo de depresión de 37º. ¿A que distancia de la base del edificio se encuentra dicho punto? Solución: Solución: 4 3 37° \ h = 64 m h \ d = 320 m 240 m 53° 48 m d Rpta.: 64 m El ángulo formado por la líneas visuales que van al extremo superior e inferior del objeto observado se denomina ángulo de observación. d = 40cot37° 4 d = 240 3 h = 48tan53° h = 48 q: Ángulo de observación. 37° Rpta.: 320 m 3 33 II BIMESTRE Línea horizontal 2 CAPÍTULO 11 ÁNGULOS VERTICALES Problema 3: Problema 4: Una persona de 2 m de estatura, observa la parte más alta de un árbol con ángulo de elevación de 37º. Si la persona está a 36 m de la base del árbol, calcula la altura de dicho árbol. Un niño de estatura h divisa una araña en el suelo con ángulo de depresión . ¿A que distancia de los pies del niño se encuentra dicha araña? Solución: Solución: h = 2 + 36tan37° h = 2 + 36 3 4 h \ h = 29 m x = hcot 36 2m x h 37° Rpta.: hcotq II BIMESTRE Rpta.: 29 m Actividad 11 1 2 Desde un punto del suelo se observa la parte más alta de una torre con ángulo de elevación . Si dicho punto se encuentra a q metros de la base de la torre, calcula la altura de la torre en terminos de y q. Desde un punto en tierra se observa lo alto de un poste con ángulo de elevación de 30º. Si la altura del poste es 6 6 m, calcula la distancia de dicho punto a la base del poste. 3 Desde lo alto de un faro se ve un barco, a 360 m de su base, con ángulo de depresión de 60º. Calcula la longitud de la línea visual. 4 Desde un punto en tierra se observa la cúspide de un cerro de 1200 m de la altura con ángulo de elevación de 53º. ¿A que distancia de la base del cerro se encuentra dicho punto? 5 6 Un ratón en tierra observa lo alto de un edificio con una ángulo de elevación q, si se acerca al edificio a una distancia de 50 m y mira otra vez lo alto de dicho edificio con un nuevo ángulo de elevación (90º – ). Si la altura del edificio es 60 m. Calcula 3tan. Una persona de estatura h observa lo alto de una torre con un ángulo de elevación f y la parte 34 3 baja se observa con ángulo de depresión . Calcula la altura de la torre en términos de h, y . 7 Desde un punto en tierra se ve la parte más alta de un edificio con ángulo de elevación de 53º. Si nos alejamos una distancia igual al duplo de la altura del edificio, el nuevo ángulo de elevación para la parte más alta del edificio es . Calcula cot. 8 Desde un punto en tierra se ve lo alto de un poste con ángulo de elevación . Nos acercamos una distancia igual a la mitad de la altura del poste y el nuevo ángulo de elevación es . Calcula H = cot – cot. 9 Una antena de teléfono de altura h se encuentra en la azotea de un edificio de altura H. Desde un punto en el suelo se ven la parte superior e inferior de la antena con ángulos de elevación y cotf respectivamente. Calcula en términos de h cotq y H. 10 Desde un punto en el suelo se ve la parte más alta de un árbol con ángulo de elevación . Nos acercamos una distancia d y el nuevo ángulo de elevación es 2. Calcula la altura del árbol en términos de y d. CAPÍTULO 12 PLANO CARTESIANO Las coordenadas en km de A y B son: (1; 5) y (3; 1), respectivamente. Calcula el largo del lago. ¿Qué son coordenadas polares? 2 Ten Presente A Ángulos horizontales Son aquellos ángulos ubicados en un plano horizontal. B Rosa naútica La recta numérica Para cada punto de la recta hay un número real y para cada número real hay un punto de la resta. –2 –1 0 Números negativos A X Números positivos Coordenada de A: 3 Rumbo Coordenada de B: –1 Para ello elegimos un punto de una recta horizontal al que lo denominamos origen y le asociamos el cero. Los números positivos se representan hacia la derecha y los negativos, hacia la izquierda. Está dado por el ángulo agudo que forma una recta y la dirección norte o sur. N Norte 2 Segundo Cuadrante (IIC) –2 1 –1 Y B Primer Cuadrante (IC) Eje de abscisas Origen X –1 –2 Dos rectas numéricas que se intersecan perpendicularmente en el origen determinan un plano denominado plano cartesiano. A 0 Tercer Cuadrante (IIIC) Cuarto Cuadrante (IVC) Eje de ordenadas Problema 2: Determina el rumbo de un punto cuyo azimut es 124º. Solución: Solución: E O 36° = 180º – 36º = 144º S Rpta.: 144° A se halla al Na°E de P B se halla al Nq°O de P C se halla al Sw°O de P Tienen la particularidad de obtenerse trazando bisectrices sucesivas. N NO 124° O E 2q q q P OSO S Rumbo de P: S56ºE NNE 2q q q O = 180º – 124º = 56º S Sur N De la figura: P w C E Este P Rumbos notables: Problema 1: Determina el azimut de un punto cuyo rumbo es S36ºE. N O Oeste Cualquier punto del plano queda determinado por el par ordenado de sus coordenadas. Coordenadas de B: (–1; –1) Coordenadas de A: (2; 2) Azimut de P: q a A B Plano cartesiano q q 2q NE ENE q q 2q SO E SE SSO S Rpta.: S56°E 3 35 II BIMESTRE Esta correspondencia biunívoca nos permite representar los números reales en la recta. Origen B Denominado compás marino, es un instrumento de orientación que permitirá localizar el objetivo. CAPÍTULO 12 PLANO CARTESIANO Problema 3: Problema 4: Sebastián camina 35 m en la dirección N55ºE, luego camina 12 m en la dirección S35ºE. Calcula la distancia del punto de partida al punto de llegada. Alex está al N66ºO de Karina. ¿Qué dirección tiene Karina respecto a Alex? Solución: Solución: O 55° 35° S d N S 66° O E S E m 55° m 35 12 N Alex O E O E Luego Karina se encuentra al S66ºE respecto a Alex. d = 37 m Rpta.: S66ºE Rpta.: 37 m Solución: Milagros camina 84 m en la dirección N48°O, luego camina 13 m en la dirección S42°O. Calcula la distancia del punto de partida al punto de llegada. De la figura: N O d2 = 842 + 132 E m Problema 5: 13 II BIMESTRE Karina S Bs alternos internos: = 66º De la figura: d2 = (35)2 + (12)2 N N 42° S 48° d 84 m N d = 85 m 48° O E S Rpta.: 85 m Actividad 12 1 Determina el azimut de un punto cuyo rumbo es S72ºO. 7 Milagros está al S72ºO de Ana. ¿Que dirección tiene Ana respecto a Milagros? 2 Determina el rumbo de un punto cuyo azimut es 296º. 8 Determina el azimut de un punto P cuyo rumbo es SO. 3 El rumbo de un punto P es N3xE y el azimut del mismo punto es (80º – 2x). Calcula x. 9 4 Alexeén camina 42 m en la dirección N68ºO, luego camina 40 m en la dirección S22ºO. Calcula la distancia del punto de partida al punto de llegada. Ricardo camina (x – 1) metros en la dirección N52ºO, luego camina 5x metros en la dirección N38ºE. Si la distancia del punto de partida al punto de llegada es de 61 metros, calcula x. 5 ¿Que ángulo forman las líneas NE y SE? 6 El rumbo de un punto es SE, determina el azimut de dicho punto. 36 3 10 Arón camina 357 m en la dirección N50ºE, luego camina otra vez 357 m en la dirección S70ºE. Calcula la distancia del punto de partida al punto de llegada. 03 Unidad Hélice de un portaviones RAZONES TRIGONOMÉTRICAS DE ÁNGULOS DE CUALQUIER MAGNITUD LA HÉLICE La hélice es un dispositivo mecánico formado por palas o álabes, montados de forma concéntrica a un eje común que al girar, trazan un movimiento rotativo en un plano. Las palas no son placas planas, sino que tienen una forma curva, sobresaliendo del plano en el que giran, esta curvatura provoca una diferencia de velocidades entre el fluido de una cara y de la otra. Esta diferencia de velocidades genera una diferencia de presiones, y por lo tanto aparece una fuerza perpendicular al plano de rotación de las palas hacia la zona de menos presión. Esta fuerza es la que mueve los barcos, eleva los helicópteros, etc. - ¿Qué artefactos de tu casa tienen hélice? http://es.wikipedia.org/wiki/H%C3%A9lice_(dispositivo) APRENDIZAJES ESPERADOS Matematiza situaciones Comunica y representa • Usa modelos de la vida cotidiana y los traslada a modelos matemáticos que emplean ángulos en posición normal y R.T. de ángulos de cualquier magnitud. • Identifica los signos de las R.T. en diferentes cuadrantes. • Emplea diagramas para simbolizar las razones trigonométricas de ángulos en posición normal y coterminales. • Utiliza esquemas gráficos para plantear problemas con reducción al primer cuadrante. Elabora y usa estrategias • Elabora diversas estrategias para resolver problemas que involucran los ángulos en posición normal y las razones trigonométricas de ángulos de cualquier magnitudy reducción al primer cuadrante. Razona y argumenta • Plantea conjeturas referentes a las R.T. de ángulos de cualquier magnitud. • Justifica el uso de las R.T. de ángulos coterminales, cuadrantales y reducción al primer cuadrante. 3 37 CAPÍTULO 13 ÁNGULOS EN POSICIÓN NORMAL ¿Cómo se calcula las R.T. de ángulo que no están en posición normal? Las hélices dan 100 revoluciones por minuto. ¿Qué ángulo barren en 24 horas? Lado terminal Lado terminal O Y O Vértice Lado inicial X Un ángulo trigonométrico está en posición normal si su lado inicial coincide con el eje positivo de la abscisas y su vértice, con el origen de coordenadas. Observación El lado terminal puede caer en cualquier cuadrante o semieje. Ángulos en posición normal, posición estándar o posición canónica A) Ángulos que pertenecen a algún cuadrante Y IIC Y Y X IIIC III BIMESTRE X Ángulo del segundo cuadrante IVC Ángulo del tercer cuadrante Problema 1: Ángulo del cuarto cuadrante Sin importar su medida, un ánX gulo pertenece a un cuadrante si, y sólo si, estando en posición normal, su lado terminal cae en dicho cuadrante. Y Lado final Vértice O Lado inicial X Solución: Y ¿A qué cuadrante pertenece un ángulo canónico que mide 248º? \ 248° III C. 248° Observación X Ángulos cuadrantales Rpta.: III C Y Y B) Ángulos cuadrantales Y Y Y X 180° 90° X X Y Y Y 540° 450° X 360° 38 270° X 3 X Los ángulos en posición normal cuyo lado terminal coincide con uno de los semiejes del plano cartesiano se denominan cuadrantales y son de la forma: q = 90°k o p k, k 2 X X Y Y X X ÁNGULOS EN POSICIÓN NORMAL CAPÍTULO 13 Problema 2: Problema 3: Problema 4: ¿A qué cuadrante pertenece un ángulo en posición estándar cuya medida es –253º? En la figura se muestra un ángulo cuadrantal, calcula el valor de x. En la figura se muestra un ángulo cuadrantal, calcula el valor de . Y Y Solución: 5(x – 8°) Y X X X –253° Solución: Solución: De la figura: 5(x – 8º) = 180º De la figura: 9(3 + 4º) = 360º + 270º x – 8º = 36º –253º II C x = 44º Rpta.: II C 3 + 4º = 40º + 30º = 22º Rpta.: 44° Rpta.: 22° Problema 5: Problema 6: Problema 7: Determina la gráfica de un ángulo en posición normal cuya medida es 840°. Determina la gráfica de un ángulo en posición estándar cuya medida es –860°. En la figura se muestra un ángulo cuadrantal, calcula f. Solución: Solución: 840° = 2(360°) + 120° –860° = 2(–360°) + (–140°) Y IIC IC 60° 840° 40° IVC IIIC 840º II C Y 5(7f + 13)° X IC –860° X De la figura: 5(7f + 13)° = 360° + 90° IVC 7f = 77 f = 11 –860º III C Rpta.: II C Solución: En la figura se cumple: De la figura: 90° Y H = 5a + 3b + q P = 3a + b – w H = 5(90°) + 3(–90°) + (–180°) ⇒ H = 0° P = 3(90°) + (–90°) – 270° ⇒ P = –90° w a 180° O calcula: M = 5H – 3P + S 3H + P + 2S Rpta.: 11 Rpta.: III C Problema 8: S = a + 2b – q 7f + 13 = 72 + 18 q 270° b 0° X 360° S = 90° + 2(–90°) – (–180°) ⇒ S = 90° Reemplazando: M= 5(0° – 3(–90°) + 90° 360° = 3(0°) + (–90°) + 2(90°) 90° M = 4 Rpta.: 4 3 39 III BIMESTRE X IIIC Y IIC Solución: Actividad 13 1 ¿A qué cuadrante pertenece un ángulo en posición normal cuya medida es 154º? 7 ¿A qué cuadrante pertenece un ángulo en posición canónica cuya medida es –325º? 2 En la figura se muestra un ángulo cuadrantal, calcula el valor de . 8 1. El vértice de un ángulo en posición estándar coincide con el origen del sistema de coordenadas. Y X 3 Indica el valor de verdad de las siguientes proposiciones: 2. 6p rad II C. 5 3. 8p rad IV C. 5 Indica el valor de verdad de las siguientes proposiciones: 1. 192º II C( ) 2. 253º III C( ) 3. 333º IV C( ) 9 Indica cuál(es) de los gráficos representan a un ángulo en posición normal: 1. 2. Y Y 4. 270º III C( ) X 4 En la figura se muestra un ángulo cuadrantal, calcula el valor de . Y 3. III BIMESTRE 4. Y Y X X X 5. 5 X 6. Y Y ¿A qué cuadrante pertenece un ángulo en posición estándar cuya medida es 1324º? X X 6 Indica el valor de verdad de las siguientes proposiciones: 1. La medida de un ángulo en posición normal es mayor que 90º. 2. El lado inicial de un ángulo estándar coincide con eje positivo de las X. 3. A un ángulo en posición normal, también se le denomina ángulo en posición estándar o canónica. 40 3 10 En la figura se muestra un ángulo canónico, calcula el valor de . Y f + 20° X 14 CAPÍTULO RAZONES TRIGONOMÉTRICAS DE ÁNGULOS DE CUALQUIER MEDIDA Q Si las coordenadas de Q respecto a P son (35; 30), ¿cuál es la pendiente de la faja transportadora? ¿Se puede calcular las R.T. de cualquier ángulo? P Observación Razones trigonométricas en el plano cartesiano Sea un ángulo del IVC, a cuyo lado terminal pertenece el punto (4; –3) con radio vector 5. A la derecha se observan las R.T. de . –3 5 • sen = • csc = 5 –3 Y 4 X 5 4 5 • cos = • sec = 5 4 (4; –3) • tan = –3 • cot = 4 4 –3 –3 Es la distancia de un punto cualquiera del plano al origen de coordenadas. Y b r O y r • sen = • csc = y r Y x r y x • cos = • sec = r y P(x; y) • tan = • cot = x X Problema 1: Solución: De la figura, calcula De la figura: x = –4; y = 3 H = sen + csc r x x y P(a; b) X a Radio vector: OP = r r2 = a2 + b2 r = a2 + b2 Radio vector: r2 = (–4)2 + 32 r=5 Y P(–4; 3) Reemplazando: H = X H= 3 5 + 5 3 34 15 Rpta.: 34/15 3 41 III BIMESTRE En general, se definen las razones trigonométricas de cualquier ángulo en base a las coordenadas de cualquier punto de su lado terminal. Radio vector CAPÍTULO 14 RAZONES TRIGONOMÉTRICAS DE ÁNGULOS DE CUALQUIER MEDIDA Problema 2: Problema 3: Problema 4: De la figura, calcula De la figura, calcula De la figura, calcula T = sen + cos R = cos + sec Y Y P(12; –5) Solución: x = 12; y = –5 Radio vector: r2 = (12)2 + (–5)2 X De la figura: x = –15; y = –8 Radio vector: r2 = (–15)2 + (–8)2 r = 13 Reemplazando: T = r = 17 –5 12 + 13 13 Reemplazando: R = R=– Rpta.: 7/13 P(24; 7) P(–15; –8) Solución: De la figura: 7 13 Y X X T= E = tan + cot 514 255 –15 17 + 17 –15 Solución: De la figura: x = 24; y = 7 Reemplazando: E = E= 625 168 7 24 + 24 7 Rpta.: 625/168 Rpta.: –514/255 III BIMESTRE Actividad 14 1 El punto P(20; 21) pertenece al lado final del ángulo canónico . Calcula E = sen + cot. 2 El punto N(–7; 3) pertenece al lado final del ángulo canónico . Calcula H = cos + tan. 3 4 5 6 gulo en posición normal cuya medida es 2(2 I C). Calcula H = 2sen + cotf. 7 El punto R(–2n; n) pertenece al lado final del ángulo en posición normal cuya medida es l. Calcula E = 5cosl – 2tanl. El punto T(–2; –3) pertenece al lado final del ángulo en posición estándar cuya medida es w. Calcula N = secw + cscw. 8 El punto H(– 3; – 2) pertenece al lado final del ángulo en posición normal cuya medida es g. Calcula E = 30(tang + cotg) seng. El punto R(5; –3) pertenece al lado final del ángulo en posición normal cuya medida es r. Calcula E = tanr + secr. 9 El punto M(6; 8) pertenece al lado final del ángulo en posición normal cuya medida es 2a, (0º < 2 < 90º). El punto E(12; 35) pertenece al lado final del ángulo en posición canónica cuya medida es a. Calcula T = csca + cota. El punto N( 3 ; 3) pertenece al lado final del án- 42 3 Calcula T = 6 5(sena + cosa) tana. 10 El punto A( 7; – 5) pertenece al lado final del ángulo en posición estándar cuya medida es r. Calcula T = 6 15(senr + cosr) cotr. 15 CAPÍTULO SIGNO DE LAS RAZONES TRIGONOMÉTRICAS ¿Qué R.T. tienen igual signo en cada cuadrante? Nota Aquí los signos de los ángulos no cuadrantales. IIC 90º Sen (+) csc IC Todas las R.T. son Positivas 180º Tan (+) Cos (+) cot IIIC sec cos 0º 360º IVC 270º sen Problema 1: cot sec csc IIIC IVC + + + + + + + – – – – + – – + + – – – + – – + – Problema 2: 3 Si tanw = , III C. Calcula 5 sen. Solución: Dato: tan = Solución: Dato : x = 9; y = –12 Radio vector: r2 = 52 + 32 r = 34 r = 15 Reemplazando: H = 5 –12 5 3 5 y 3 = x 5 Radio vector: r2 = 92 + (–12)2 H= IIC –12 9 × 15 15 Rpta.: –12/5 Luego sen = – sen = – 3 34 – – Signo de SENO en cuadrantes – + – + Signo de COSENO en cuadrantes. – + + – 3 34 34 Rpta.: –3 34/34 Solución: Señale el signo de la expresión 130º II C cos130º es (–) cos130° tan220° + Signo de TANGENTE en cuadrantes. Problema 3: E= + 220º III C tan220º es (+) Luego: E = (–) E = (–) (+) Rpta.: (–) 3 43 III BIMESTRE Si P(9; –12) pertenece al lado final de un ángulo canónica cuya medida es , calcula H = 5sen cos. tan IC CAPÍTULO 15 SIGNO DE LAS RAZONES TRIGONOMÉTRICAS Problema 4: Solución: es la medida de un ángulo en posición normal, tal que sen < 0 cos > 0. ¿A que cuadrante pertenece dicho ángulo? sen < 0 III C o IV C cos > 0 I C o IV C IV C Rpta.: IV C Problema 5: Problema 6: Señala el signo de la expresión: w es la medida de un ángulo en posición canónica, tal que tanw > 0 ∧ secw < 0. ¿A qué cuadrante pertenece dicho ángulo? H= sen154° · cos205° · tan118° sec224° · cot196° · csc101° Solución: Solución: (+)(–)(–) (–)(+)(+) (+) H= (–) tanw > 0 w I C o III C H= secw < 0 w II C o III C w III C H = (–) Rpta.: IIIC Rpta.: (–) Actividad 15 III BIMESTRE 1 Señale el signo de la expresión T = sen280° . cos200° 7 Señale el signo de la expresión R= 2 3 2 Si sen = , II C. Calcula 5tanf. 3 Si P(–3; 2) pertenece al lado final del ángulo en posición normal cuya medida es a. Calcula E = 26sena cosa. 5 Señale el signo de la expresión tan80° cos140º R= sen110° 6 44 8 w es la medida de un ángulo en posición normal, tal que senw > 0 cotw < 0. Determina a que cuadrante pertenece dicho ángulo. 9 Si P (– 3; – 5) pertenece al lado final del ángulo en posición normal cuya medida es f. Calcula T = 8senf – 4cosf . es la medida de un ángulo estándar, tal que cos < 0 tan > 0. Determina a que cuadrante pertenece dicho ángulo. 4 1 Si cosr = , r IV C. Calcula 15cotr. 4 3 cos170° cot230º sen300° sec340º 10 Señale el signo de la expresión R= sec105° tan205º cos305° sen95º 16 CAPÍTULO R.T. DE ÁNGULOS COTERMINALES Y CUADRANTALES ¿Dos ángulos de signos opuestos pueden ser coterminales? ¿Cuál es la pendiente de la caída? Y 40º X 400º RT(400º) = RT(40º) RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COTERMINALES Dos ángulos en posición normal que tienen el mismo lado terminal se denominan coterminales y se diferencian en un número entero de vueltas. Como tienen el mismo lado final los ángulos coterminales tienen las mismas razones trigonométricas. Los ángulos 40º y 400º son coterminales porque tienen el mismo lado final. En general: Dos ángulos a y b son coterminales si: Y De modo que: P(x; y) ¿Son coterminales lo ángulos? o |a – b|= 2pk k ∈ + |a – b| = 360° k X Nota Y 240° R.T. (a) = R.T. (b) X III BIMESTRE Problema 1 Si y son las medidas de ángulos coterminales, calcula sen cosw P= + senw cosf Solución: Si y son medidas de ángulos coterminales, se cumple RT() = RT(). Luego: P = sen senw + cosw cosf Y =1+1 Rpta.: 2 –120° X RAZONES TRIGONOMÉTRICAS DE ÁNGULOS CUADRANTALES Y Y (1; 0) 0º X (0; 1) 90º X 0° o 360° 90° senq 0 1 0 –1 cosq 1 0 –1 tanq 0 nd 0 Y Y 180º (0; –1) X (–1; 0) 180° 270° X 270º 0° o 360° 90° 180° 270° cotq nd 0 nd 0 0 secq 1 nd –1 nd nd cscq nd 1 nd –1 nd: No definido 3 45 CAPÍTULO 16 R.T. DE ÁNGULOS COTERMINALES Y CUADRANTALES Problema 2 Calcula E = Problema 3 Calcula T = sen777º – sen57º 3cos180° – sen90º 2cos360° Solución: Solución: Se observa: Utilizando la tabla de las razones trigonométricas de ángulos cuadrantales, se tiene: 777º – 57º = 720º = 2(360º), entonces 777º y 57º son las medidas de ángulos coterminales. Luego: T = sen57º – sen57º E = 3(–1) – (1) 2(1) T = 0 E = –2 Rpta.: 0 Rpta.: –2 Problema 4 Solución: En la figura, calcula 2senr tanq P= – senq tanr r y q son medidas de ángulos coterminales, entonces: RT() = RT() Y Luego R = X 2senr R=1 senr – tanr tanr =2–1 Rpta.: 1 III BIMESTRE Actividad 16 1 2 Calcula H = 3sen90° cos0° – . sec0° csc90° 6 calcula T = Calcula R = cos440º – cos80º. 7 3 a y son las medidas de ángulos coterminales, Calcula E = 7sen90º – 3cos180º + 5tan180º. tana tanb + cosa sec Indica el valor de verdad de las siguientes proposiciones: 1. tan720º = –1 2. sen990º = –1 4 Calcula R = cos[2sen(tan)] 5 Indica el valor de verdad de las siguientes proposiciones: 8 p Calcula P = sen{cot } – cos{tan(sen2)} 2 1. sen270º = 1 9 Calcula H = tan55º – 2tan775º + tan415º 3. cos540º = –1 2. cos180º = –1 3. tan2 = 1 46 10 Calcula R = sec428º – csc22º + cos22º csc428º 3 17 CAPÍTULO REDUCCIÓN AL 1ER CUADRANTE DE ÁNGULOS MENORES QUE UNA VUELTA ¿Qué R.T. de 60° y 120° son iguales? 130° ¿Cuánto vale la cosecante de la abertura del valle? Recuerda Y sen210° = 210° – 3 210° 30° 60° 2 (– 3; –1) X 180° + 30° IIC 90º 270° – 60° cos60° = 1 sen30° = 2 –1 Signos de las razones trigonométricas en los cuatro cuadrantes –1 2 1 2 Signo porque 210° IIIC R.T.(90° + q) =coR.T.(q) –1 240° signo (–1; – 3 ) El signo depende únicamente del cuadrante al que pertenece el ángulo a reducir. • 240° IIIC seno es negativo (–). • 240° = – 3 270° – 30° o 180° + 60° 2 30° R.T.(270° q) =coR.T.(q) signo • Elegimos 270° – 30° sec IVC Ángulos positivos mayores que 90° y menores que 360° 90° < q < 360° Se cumple: 1. Si q IIC sen(270° – 30°) = –cos30° = – 3 2 Co-razón porque 270° R = 2cos30º + 3(–cos30º) Calcula R = 2sen120º + 3cos210º R = –cos30º Solución: R=– 3 2 R.T.(q) = R.T.(180° – q) 2. Si q IIIC R.T.(q) = R.T.(q – 180°) Problema 1: R = 2sen(90º + 30º) + 3cos(180º + 30) cot IIIC 270º Y X 60° signo R.T.(360° – q) =R.T.(q) Tan (+) C os (+) Observación • Calculamos sen240°: R.T.(180° q) =R.T.(q) 0º 360º Rpta.: – 3/2 3. Si q IVC R.T.(q) = R.T.(360° – q) El signo () dependerá del ángulo y de la R.T. pedida. 3 47 III BIMESTRE Co-razón cuando ángulo cuadrantal es 90° o 270° signo todas sen210° = sen(270° – 60°) = –cos60° Misma razón cuando ángulo cuadrantal es 180° o 360° En general: Positivas Signo porque 210° IIIC Ángulo cuadrantal sen210° = sen(180° + 30°) = –sen30° csc IC 180º En la figura se puede observar que sen210º, sen30º y cos60º son iguales en valor absoluto, sólo difieren en el signo. Ángulo cuadrantal Sen (+) CAPÍTULO 17 REDUCCIÓN AL 1ER CUADRANTE DE ÁNGULOS MENORES QUE UNA VUELTA Problema 2: Problema 3: Calcula Reduce M = 3cos150º – 4sen300º T= Solución: T= M = –3cos30º + 4cos30º M = cos30º cscf cscf T=1 3 2 Rpta.: 1 Rpta.: 3/2 Problema 4: Solución: Reduce H= csc(180º – ) Solución: M = 3cos(180º – 30º) – 4sen(360º – 60º) M = 3(–cos30º) – 4(–sen60º) M= sec(270º + ) sen(360º – q) cos(180º + q) H= + sen(90º + ) sec –senq + cosq secq –cosq H = tanq + 1 Rpta.: 1 + tanq III BIMESTRE Actividad 17 1 Calcula M = 6sen150º – 2cos240º. 2 Calcula R = 8tan300º + 6cot210º. 2. cos(2 + a) = –cosa 3 Reduce p 3. cot( + ) = tan 2 H= 4 1. sen( sec(180º– ) + tanf tan(90º – f) csc(90º + f) Indica el valor de verdad de las siguientes proposiciones: 7 Calcula T = 5cos127º + 8sen150º – 3tan225º. 8 Calcula H = sen300º cot135º + cos330º tan315º 9 Reduce 1. sec(90º + ) = –csc p 2. tan( – ) = –cot 2 3. sen(360º – ) = sen 5 Reduce 3cos40° 6sen50° 2tan20° T= + + . cos140° sen130° tan160° 6 48 Indica el valor de verdad de las siguientes proposiciones: 3 3p + w) = cosw 2 3p – q) sen(p + q) 2 E= sen( – ) cos(2 – ) tan( – ) cos(2 + ) tan( 10 Señale M= 3tan66° 2cos33° sen22° + + tan294° cos327° sen338° 18 ¿Puede ser positivo la razón trigonométrica de un ángulo negativo? C A Cuándo la hélice haya dado 2124,25 vueltas, ¿cuánto valdrá el seno del ángulo determinado por la paleta C? CAPÍTULO REDUCCIÓN AL 1ER CUADRANTE DE ÁNGULOS MAYORES QUE UNA VUELTA 120° ¡! Interesante Ángulo en radianes B Para ángulos mayores que una vuelta se establece la siguiente relación: R.T.(360ºk + q) = R.T.(q); k R.T.(2pk + q) = R.T.(q); k Por lo tanto, para reducir al primer cuadrante se le quita el máximo número de vueltas y se calcula las razones trigonométricas del resto y si éste no cae en el primer cuadrante se reduce como en el capítulo anterior. Cuando el ángulo está en radianes, para quitar el número de vueltas se divide entre 2p. En forma práctica se divide el numerador entre el doble del denominador y se reemplaza con el residuo el numerador. Véase el siguiente ejemplo: • tan • Calculamos cos750°: • Calculamos sec2280°: Y 1 ( 3 ; 1) 2 30° 720° 3 X 750° 360° 30° 2280° 360° 120° 6 = – csc(30°) = –2 signo 2 • tan 73 12 1 6 403p 3 p = tan p = tan(p – ) = –1 4 4 4 403 8 3 120° IIC y en este cuadrante sec es (–) 50 1 403p p tan = – tan = –1 4 4 signo \ sec2280° = –2 3p/4 IIC y en este cuadrante tan es (–) 2 Problema 1: Problema 2: Calcula H = 4cos420º + 6sen750º Calcula M = 5sen1133º – 8tan757º Solución: Solución: H = 4cos(360º + 60º) + 6sen[2(360º) + 30º] M = 5sen[3(360º) + 53º] – 8tan[2(360º) + 37º] H = 4cos60º + 6sen30º M = 5sen53º – 8tan37º 1 1 H = 4 + 6 2 2 4 3 M=5 –8 5 4 H=5 M = –2 Rpta.: 5 Rpta.: –2 3 49 III BIMESTRE 3 cos750° = cos30° = 2 sec2280° = sec120° = sec(90° + 30°) 3 73p 1 = tan p = 6 6 3 CAPÍTULO 18 REDUCCIÓN AL 1ER CUADRANTE DE ÁNGULOS MAYORES QUE UNA VUELTA Problema 3: Problema 4: Calcula R = 6sec4020º csc4350º Calcula T = 4sen1590º + 10cos2287º Solución: Solución: R = 6sec[11(360º) + 60º] csc[12(360º) + 30º] T = 4sen[4(360º) + 150º] + 10cos[6(360º) + 127º] R = 6sec60º csc30º T = 4sen150º + 10cos127º R = 6(2)(2) T = 4sen30º + 10(–cos53º) R = 24 1 3 T=4 – 10 2 5 Rpta.: 24 T = –4 Rpta.: –4 Y • senq = (8; 15) 15 sen(–q) = 17 X 8 O 17 III BIMESTRE –15 15 17 8 • cosq = 17 8 cos(–q) = 17 • tanq = (8; –15) • sen(–53°) = –sen53° = – –15 17 15 8 –15 tan(–q) = 8 4 5 Las R.T. para ángulos negativos se obtienen de la siguiente manera: sen(–q) = –senq csc(–q) = –cscq Observación cos(–q) = cosq sec(–q) = secq tan(–q) = –tanq cot(–q) = –cotq Las razones trigonométricas de ángulos negativos, también se puede obtener calculando las R.T. de su coterminal positivo: • Calculamos csc(–30º): • cos(–45°) = cos45° = 2 2 330° –30° • tan(–120°) = – tan120° = –tan(180° – 60°) = –[–tan60°] = 3 csc330º = csc(360º – 30º) Problema 5: Problema 6: Calcula Calcula R = 5sen(–37º) csc(–30º) Solución: csc330º = –csc30º = –2 IV C (–) M = 12sec(–60º) cot(–45º) cos(–30º) Solución: R = 5(–sen37º)(–csc30º) M = 12sec60º (–cot45º) cos30º R = 5– 3 (–2) 5 M = 12(2)(–1) R=6 Rpta.: 6 50 3 3 2 M = –12 3 Rpta.: –12 3 REDUCCIÓN AL 1ER CUADRANTE DE ÁNGULOS MAYORES QUE UNA VUELTA Problema 7: CAPÍTULO 18 Solución: Calcula p R = cos + cos 2p + cos 3p + cos 4p 5 5 5 5 p p R = cos + cos 2p + cos p – 2p + cos p – 5 5 5 5 p p R = cos + cos 2p – cos 2p –cos 5 5 5 5 R=0 Rpta.: 0 Problema 8: Calcula p p p 13p M = sen + sen + sen + sen 5p + sen 9p + sen 7 5 3 7 3 5 Solución: p p p p p p M = sen + sen + sen + sen 2p – + sen 2p – + sen 2p – 7 5 3 3 5 7 p p p p p p M = sen + sen + sen – sen – sen – sen 7 5 3 3 5 7 M=0 Rpta.: 0 Actividad 18 Calcula P = 2sen390º – 6cos780º. 2 Calcula H = 3tan773º – 12cot397º. 3 Indica el valor de verdad de las siguientes proposiciones: 6 Calcula M = sen 7 p 23p p p + sen + sen + ... + sen 12 6 4 12 Reduce 1. sen(720º + q) = senq 2. tan(1440º – q) = tanq T= 3. sec(360º + ) = –sec 4 Calcula R = sen2000º cos1080º sec430º. 5 Indica el valor de verdad de las siguientes proposiciones: 1. cos(450º + f) = –senf sen80° cos40° tan20° + + sen(–280°) cos(–320°) tan(–340°) 8 Calcula M = sen(–585º) cos(–660º) tan(–495º) 9 Calcula H = sen [cot(–40º)] + sen [cot(–320º)] 10 Calcula M = cot[csc(–20º)] + cot[csc(–340º)] 2. cot(4 + f) = tanf 7p 3. csc( – ) = sec 2 3 51 III BIMESTRE 1 04 Unidad Machu Picchu. Maravilla del Mundo IDENTIDADES TRIGONOMÉTRICAS IDENTIDAD CULTURAL La Identidad cultural tiene que con la respuesta a las preguntases ¿quién soy yo? ¿De dónde vengo? y cuyas respuestas dependen totalmente del autoconocimiento. El primer elemento que tiene el Perú, como fundamento, que sustenta su plural y rica identidad, es el haber sido cuna de una civilización única y original en el mundo: la andina. Los problemas que afectan a nuestra identidad son la masificación del abuso cultural vía la imitación de valores ajenos que nos han hecho sentir y creer que son superiores a los nuestros. ial de la Humanidad. imonio cultural inmater Danzante de tijeras, patr - Describe tu identidad cultural. http://identidadculturalfacem.blogspot.com/ APRENDIZAJES ESPERADOS Matematiza situaciones • Traslada situaciones de la vida cotidiana a modelos matemáticos que usan las identidades trigonométricas y auxiliares. • Identifica las identidades para el ángulo doble. y la srazones trigonométricas de ángulos compuestos. 52 3 Comunica y representa Elabora y usa estrategias Razona y argumenta • Utiliza esquemas gráficos para representar las identidades trigonométricas. • Elabora demostraciones de identidades trigonométricas. • Elabora organizadores visuales para representar las distintas identidades trigonométricas. • Emplea diversas estrategias para resolver problemas que involucran el uso de las identidades trigonométricas. • Determina las razones trigonométricas de ángulos compuestos. • Justifica el uso de las identidades trigonométricas. • Propone conjeturas sobre las razones trigonométricas de ángulos compuestos. • Plantea ejemplos sobre las identidades trigonométricas. 19 CAPÍTULO IDENTIDADES TRIGONOMÉTRICAS PITAGÓRICAS ¿Cuál es la diferencia entre identidad algebraica e identidad trigonométrica? Si senq cosq = 0,5 y a + b = 10 m, calcula d. d b q a Veamos la demostración de una de las identidades pitagóricas: c A • sen2x = a x a2 c2 b2 • cos2x = 2 c sen2x + cos2x = Recuerda a2 b2 + c2 c2 c2 a2 + b2 sen2x + cos2x = c2 c a sen2x + cos2x = 1 C b B a2 + b2 = c2 b c2 = a2 + b2 sen2x + cos2x = 1 sec2x – tan2x = 1 csc2x – cot2x = 1 c2 – a2 = b2 Identidades pitagóricas c2 – b2 = a2 Estas igualdades se denominan identidades pitagóricas y se cumplen para todos los valores angulares de x, a excepción de los valores donde la R.T. no está definida. Problema 1: Problema 2: Simplifica M = sen4f cos4f – senf + cosf Reduce + cosf H= Solución: Identidad algebraica: Solución: a2 – b2 = (a + b)(a – b) H = tan2f 1 1 – secf – 1 secf + 1 H = tan2f secf + 1 – secf + 1 (secf – 1)(secf + 1) Aplicando: M= (sen2f + cos2f)(sen2f – cos2f) (senf + cosf) + cosf M= (1)(senf + cosf)(senf – cosf) (senf + cosf) + cosf ⇒ H = (sec2f – 1) 2 sec2f –1 H=2 ⇒ M = senf – cosf + cosf M = senf tan2f tan2f – secf – 1 secf + 1 Rpta.: 2 Rpta.: senf 3 53 CAPÍTULO 19 IDENTIDADES TRIGONOMÉTRICAS PITAGÓRICAS Problema 3: Problema 4: Simplifica Reduce R= 3f cos3f sen – senf – cosf – T = csc4f – sen2f – cot4f – cos2f tanf cot(90° – f) Solución: Solución: Agrupando convenientemente Identidad algebraica T = (csc4f – cot4f) – (sen2f + cos2f) a3 – b3 = (a – b)(a2 + ab + b2) T = (csc2f – cot2f)(csc2f + cot2f) – (1) Aplicando: M= M= T = (1)(csc2f + cot2f) – 1 (senf – cosf)(sen2f + senfcosf + cos2f) (senf – cosf) sen2f + cos2f – tanf tanf ⇒ T = 1 + cot2f + cot2f – 1 T = 2cot2f + senfcosf – 1 Rpta.: 2cot2f ⇒ M = 1 + senfcosf – 1 M = senfcosf Rpta.: senfcosf Actividad 19 1 Reduce M = sen2f + cos4f – sen4f 7 Simplifica H= 2 Simplifica H= 3 4 sen6f – cos6f (1 + senfcosf)(sen3f + cos3f) 8 Reduce R = tanf senf cos2f + cos3f Reduce N= 3θ 6 1. 1 – cos2x = sen2x ( ) 2. tan2x – sec2x = 1 ( ) 3. sen2x + cos4x = cos2x + sen4x ( ) cos – secθ sen3θ – cscθ sen2θ Reduce R= Indica el valor de verdad de las siguientes proposiciones: cos2θ 9 5 (1 + tan2f)sen2f cosf cotf (1 – cos2f)(1 + cot2f) cosf tanf + cotf cosf senf secf cscf Reduce R = tan2f + sen2f + cos4f cos2f + sen4f 10 Simplifica Reduce M= 54 2sen2f + tan2f + 2cos2f + cot2f sec2f csc2f 3 E= cscf(sen4f + senfcos3f) (senf – cosf)2 + senf cosf 20 CAPÍTULO IDENTIDADES TRIGONOMÉTRICAS RECÍPROCAS Y POR COCIENTE ¿Para que valor de x no se cumple senx cscx = 1? q Veamos la demostración de una de las identidades recíprocas: B a2 + b2 = c2 • senx = c A a x senx⋅cscx = • cscx = c a C b a c a c × c a senx⋅cscx = 1 2 Identidades trigonométricas recíprocas senx⋅cscx = 1 cosx⋅secx = 1 tanx⋅cotx = 1 Estas igualdades se denominan identidades recíprocas y se cumplen para todos los valores angulares de x, a excepción de los valores donde la R.T. no está definida. Problema 1 Problema 2 Reduce Simplifica M = cos tan csc – cos sen(90º – ) sen·cos·sec2 H= tanf Solución: sen·sec·cos·sec H= tanf Solución: M = cos · senf · csc – cos · cos cosf M = 1 – cos2 H= M = sen2 Rpta.: sen2 Ten Presente Las identidades trigonométricas recíprocas también se pueden expresar en la forma siguiente: senx = 1 csc x cosx = 1 sec x tanx = 1 cot x 1 ·(1) sen· cosf tanf H= tanf =1 tanf Rpta.: 1 Identidades trigonométricas por cociente tan x = senx cos x cot x = cosx senx 3 55 CAPÍTULO 20 IDENTIDADES TRIGONOMÉTRICAS RECÍPROCAS Y POR COCIENTE Véase las demostraciones: a2 b2 + B c2 = c a x A C b a a c • tan x= = b b c senx ⇒ tan x = cos x b b c • cot x= = a a c cosx ⇒ cot x = senx Problema 3 Problema 4 Reduce R = sen3·tan·csc + cos3·tan·sec cos·cot – sen·cos2 cos2·cot2 Solución: Solución: R= Reduce M = tan·sen2·sen·csc + tan·cos2·cos·sec R = tan·sen2·(1) + tan·cos2·(1) R = tan·(sen2 + cos2) sen2·cos cos – senf senf cos·(cot – sen·cos) M= = 2 cos2 cos·cos·cot cosf· sen2f M= R = tan·(1) R = tan cos·(1 – sen2)·sen cos·cos2 M = sen Rpta.: sen Rpta.: tan Actividad 20 1 6 Reduce H = sen·cos·tan·sec·cot·csc 2 Simplifica M= 3 sen·cot + cos·tan senf Reduce R = senr·cosr·tanr·cscr 4 M= 7 send·cosd – cosd·cotd. 1 – cosd Reduce R= 8 tanf tanf – secf – 1 secf + 1 Reduce H= cos·cot – sec2·cos·cot sen·tan – csc2·sen·tan Simplifica M= 5 Simplifica sen cos tan + + – sen2·sec2 cscf secf cotf Reduce Reduce M= cosf·cscf cosf·cscf – 1 – senf 1 + senf 10 Simplifica P= 56 9 2sen3w·cosw – senw·cosw cosw – 2cos3w 3 H= sen·(1 + tan) + cos·(1 + cot) tan·csc ¿Cómo se distingue una identidad de una ecuación trigonométrica? 125304 21 CAPÍTULO IDENTIDADES TRIGONOMÉTRICAS AUXILIARES Matemática en la vida Instrumentos auxiliares de la topografía El planímetro es un aparato que mide el área de regiones con contorno irregular. A partir de las identidades fundamentales se derivan un conjunto de identidades, llamadas auxiliares, que son frecuentes en la reducción de expresiones trigonométricas y útiles en la solución de las ecuaciones trigonométricas. Aquí las identidades auxiliares: sen4x + cos4x = 1 – 2sen2xcos2x; x R sen6x + cos6x = 1 – 3sen2xcos2x; x R (1 senx cosx)2 = 2(1 senx)(1 cosx); Problema 2: Reduce Reduce sen·tan + cos sec·csc Solución: cos sen·(tan + ) senf M= sec·csc M= sen·(tan + cot) (tan + cot) La brújula es un instrumento de orientación. Mide ángulos horizontales respecto al norte. x R Problema 1: M= El eclímetro o nivel de mano mide el ángulo de inclinación. np ; n 2 x R – np ; n 2 sec2x + csc2x = sec2xcsc2x; x R – tanx + cotx = secxcscx; El curvímetro es un aparato que mide la longitud de curvas en el plano H = sen2·cos2·(2 + tan2 + cot2) Solución: H = sen2·cos2·(1 + tan2 + 1 + cot2) H = sen2·cos2·(sec2 + csc2) H= sen2·cos2·(sec2·csc2) H = (sen·csc)2·(cos·sec)2 El GPS es un aparato que proporciona las coordenadas de cualquier punto de la superficie terrestre H = (1)2·(1)2 H=1 M = sen Rpta.: senf Rpta.: 1 3 57 CAPÍTULO 21 IDENTIDADES TRIGONOMÉTRICAS AUXILIARES Problema 3: Simplifica R = sen4q + cos4q sen6q + cos6q – 3 2 125304 Solución: R= R= \R= 1 – 2sen2q·cos2q 2 – Matemática en la vida El jalón es una estaca alargada que sirve para alinear. 1 – 3sen2q·cos2q 3 1 1 – sen2q·cos2q – + sen2q·cos2q 2 3 1 1 1 – R= 2 3 6 Rpta.: 1/6 La wincha sirve para medir distancias. Problema 4: Simplifica T = 2senf cosf (1 + senf – cosf) 1 + cosf 1 – senf Solución: Elevando al cuadrado: T2 = 4sen2f cos2f 2(1 + senf)(1 – cosf)(1 + cosf)(1 – senf) T2 = 2sen2f cos2f =2 T= 2 (1 – sen2f)(1 – cos2f) Rpta.: 2 Actividad 21 1 Si csc – sen = 6, calcula sen2 + cot2 tan·sec2 7 H = sec2·csc – cos·cot – sen·tan2 csc2·tan + tan + cot 2 Simplifica M = 3 2(1+ sen)·sen2 Reduce M = (sen – cos + 1)2 4 Reduce T = 8 5 6 58 sec·csc – cot sec Simplifica M = Simplifica R = Simplifica sen·sec2·csc2 – sen·cot2 cos + sec sen4 + tan2 + cos4 – sec2 cot2 + sen6 – csc2 + cos6 3 Simplifica M = sen2·sec2 + 9 sec·csc – cot ·cot2 sec·csc – tan Si tan + cot = 10, calcula sen4 + cos4 10 Si tanr + cotr = 15, calcula sen6r + cos6r 22 CAPÍTULO R.T. DE ÁNGULOS COMPUESTOS (SENO Y COSENO) ¿Cuál es el desarrollo de sen(x + y + z)? 32 m 23° 37° Para la suma Para la diferencia 2 sen(x + y) = senxcosy + senycosx sen(x – y) = senxcosy – senycosx cos(x + y) = cosxcosy – senxseny cos(x – y) = cosxcosy + senxseny Ten Presente Propiedades: sen(x + y)sen(x – y) = sen2x – sen2y Problema 1: Problema 2: 2 5 Si sen = , senw = , (, w I C). 3 6 Reduce Calcula sen(f + w). M = sen30º·cosx + senx·cos30º + sen30º·cosx – senx·cos30º 6 2 f 5 w 1 1 sen(f + w) = senf cosw + senw cosf sen(f + w) = sen(f + w) = M = sen(30º + x) + sen(30º – x) Solución: Solución: 3 cos(x + y)cos(x – y) = cos2x – cos2y 2 1 5 1 × + × 3 6 6 3 2 + 10 6 Rpta.: M = 2sen30º·cosx Observación M = 2· 1 ·cosx 2 M = cosx Rpta.: cosx Las identidades de los ángulos compuestos son de vital importancia al ser aplicados a los ángulos notables. • Determina cos16° 2 + 10 6 16° = 53° – 37° cos16° = cos(53° – 37°) Problema 3: Simplifica H = cos16° = sen( + w) – senw·cos cos( + w) + senf·senw cos16° = Solución: H= senf·cosw + senw·cos – senw·cos cosf·cosw – senf·senw + senf·senw H= senf·cosw senf = H = tan cosf·cosw cosf 3 4 4 3 + 5 5 5 5 24 25 Rpta.: tan 3 59 CAPÍTULO 22 R.T. DE ÁNGULOS COMPUESTOS (SENO Y COSENO) Problema 4: En un triángulo rectángulo ABC, recto en B, se traza la mediana CM; tal que MA = BC y mBMCA = . Calcula cos. Solución: C 2 1 cos() = cos(w – a) cos = cosw·cosa + senw·sena 5 A ACM: = w – a M 1 1 B cos = cos = 1 2 1 1 × + × 2 5 2 5 3 10 10 Rpta.: 3 10 10 Actividad 22 1 Reduce M = 2 Si tan = sen( + w) – senw·secw cos·cosw 1 1 y tanw = (0º < f; w < 90º), 2 3 6 Calcula M = 34sen8º·sen14º 7 Simplifica H = 8 Reduce sen( – w) + senw·cosf sen2·cosw calcula sen( – w). sen( – w) sen·senw 3 Reduce M = cosf·cscf + 4 Si csca = 5 y cscb = 10 (0º < a; b < 90º), calcula cos(a + b). 5 Reduce M = 60 cos(r – g) – seng·secg senr·cosg 3 H= 9 cos(45º + f) + cos(45º – f) sen·cosf Si 5sen – 5 3 cos = 12 , calcula 35cos(150º – f) 7 10 Si 2sen( + w) = 5sen( – w), calcula 3tan·cotw. 23 CAPÍTULO TANGENTE DE LA SUMA Y DIFERENCIA DE DOS ARCOS ¿Para qué valores de xey tan(x + y) = tanx + tany? 30° 4m 30 m Tangente de la suma de dos arcos tan(x + y) = Tangente de la diferencia de dos arcos tanx + tany 1 – tanx tany tan(x – y) = tanx – tany 1 + tanx tany Propiedades: 2 tanx + tany + tanx · tany · tan(x + y) = tan(x + y) Ten Presente tanx – tany – tanx · tany · tan(x – y) = tan(x – y) tanq tanf = Problema 1: Problema 2: Si tan = 2 y tanw = 2. Si tan = 5 y tan(f – w) = 3. Calcula –7tan(f + w). Calcula 8tanw. Solución: Solución: tan(f + w) = tan(f + w) = tanf + tanw 1 – tanf tanw tan(f – w) = 2+2 1 – 2 (2) \ –7tan(f + w) = 6 + 5 2 Rpta.: 6 + 5 2 3= sen(q f) cosq cosf tanf – tanw 1 + tanf tanw 5 – tanw 1 + 5tanw 3 + 15tanw = 5 – tanw \ 8tanw = 1 Rpta.: 1 Problema 3: Reduce M = [tan(45º + ) + tan(45º – )](1 – tan2). Solución: M= tan45º + tanf tan45º – tanf + 1 – tan45º·tanf 1 + tan45º·tanf M= 1 + tanf 1 – tanf 2 + 2tan2 + (1 – tan2) = (1 – tan2) 1 – tanf 1 + tanf 1 – tan2 M = 2sec2 (1 – tan2) Rpta.: 2sec2 3 61 CAPÍTULO 23 TANGENTE DE LA SUMA Y DIFERENCIA DE DOS ARCOS Problema 4: Si y w son complementarios y 2sen = 3senw. Calcula tan( – w). Solución: + w = 90º senw = cosf Si 2sen = 3cos tan = 3 3 2 cotf = tanw = 2 2 3 tan – tanw Luego tan(f – w) = = 1 + tan·tanw tan(f – w) = 3 2 – 2 3 3 2 1+ 2 3 5 12 Rpta.: 5/12 Actividad 23 1 Si tan = 2 y tanw = 3, calcula 6tan( + w). 2 Si tana = 6 y tanb = 5, calcula 31tan(a – b). 3 Si tanr = 5 y tan(r + g) = 13, calcula 24tang. 4 Si tand = 7 y tan(d – g) = 5, calcula 12tang. 7 En el lado AD de un rectángulo ABCD se ubica un punto N; tal que CN BD = {T}, 3NA = 2ND, CD = 2AN y mBBTC = d. Calcula tand. 8 Si tan(a + b) = 6 y tan(a – b) = 3, calcula 17tan2. 9 Si a + b + g = p, calcula M=2 5 6 En un triángulo rectángulo ABC, recto en B, se traza la ceviana interior AT; tal que mBTAC = f, TB = 2TC y AB = 3TC. Calcula tanf. En el lado AD de una cuadrado ABCD se ubica un punto T; tal que 2TD = 3TA y mBBTC = r. Calcula 19tanr. 62 3 sen(a + b) tan(a + g) cos(a + b + 2g) +3 +4 seng tanb cosg 10 Las longitudes de las bases de un trapecio rectángulo de diagonales perpendiculares entre sí son 4 y 9. Calcula la tangente de la medida del ángulo formado por el lado lateral oblicuo y la diagonal menor. 24 CAPÍTULO IDENTIDADES PARA EL ARCO DOBLE ¿Cuándo se duplica el ángulo, se duplica la R.T? q 40 m 100 m Recordemos que: 2 En las R.T. de la suma de dos arcos, haciendo que los arcos sean iguales obtenemos las R.T. del arco doble, tal como se ha procedido a la izquierda para obtener el coseno del arco doble. cos( + b) = cos cosb – senb sen Para b = , tenemos: cos( + ) = cos cos – sen sen cos2 = cos2 – sen2 Seno de 2x Coseno de 2x cos2x = cos2x – sen2x sen2x = 2senx · cosx Problema 1: 1 Si senf = , (f ∈ IC), 3 Solución: 1 f 2 tan2x = Propiedades (senx + cosx)2 = 1 + sen2x (senx – cosx)2 = 1 – sen2x Triángulo del ángulo doble 2tanx 1 – tan2x H = 2senfcosf + cos2f – sen2f calcula H = sen2f + cos2f. 3 Tangente de 2x Ten Presente 2 1 2 + 2 – 1 ⇒ H=2 3 3 3 3 2 2 2+1 H= 3 Rpta.: (2 2 + 1)/3 Fórmulas de degradación 2sen2x = 1 – cos2x 2cos2x = 1 + cos2x Problema 2: 5 Si senf + cosf = , 6 calcula M = 36sen2f Solución: (senf + cosf)2 = sen2f + cos2f + 2senfcosf = 5 6 25 36 ⇒ 1 + sen2f = 2 25 36 36senf = –11 Luego M = –11 Rpta.: –11 3 63 CAPÍTULO 24 IDENTIDADES PARA EL ARCO DOBLE Problema 3: Problema 4: Simplifica 3 , (f ∈ IC), 7 Si senf = R = 16cos10°cos20°cos40°cos80° calcula tan2f. Solución: Se sabe: sen2f = 2senfcosf Solución: 7 ⇒ cosf = 3 f Aplicando: 2 2tanf 1 – tan2f tan2f = R = 16 3 2 2 ⇒ tan2f = 3 1– 2 sen2f 2senf R= 2 ⇒ R= sen20° sen40° sen80° sen160° ⋅ ⋅ ⋅ 2sen10° 2sen20° 2sen40° 2sen80° sen160° sen10° sen20° (2sen10°cos10°) = sen10° sen10° R = 2cos10° tan2f = 4 3 Rpta.: 2cos10° Rpta.: 4 3 Actividad 24 1 2 1 Si tanf = , f < 90°, calcula 5sen2f. 2 6 E = sen2fcscf + senfcotf 7 Simplifica M= 8 3 Si senf + cosf = , calcula 4sen2f. 2 4 1 Si tanf = ; f < 90°, calcula 4tan2f. 3 5 Reduce 64 (senf + cosf)(senf – cosf) senfcosf 3 Simplifica M= 9 H= Reduce R = 3cosftanf + 1 – cos2f 1 + cos2f + 1 – cos2f 1 – sen2f 3 Reduce cos2f – 1 senf cos4f – sen4f senfcosf En un triángulo rectángulo ABC, recto en B, se traza la bisectriz interior AT; tal que TC = 3TB y mBTAC = f. Calcula senf + sen2f. 10 En el lado AB de un trapecio rectángulo ABCD, recto en A y B, se ubica un punto T, tal que el ángulo CTD es recto; mBTDA = f; mBTDC = 2f y 2AD = 3BC. Calcula M = 2tanf + 3tan2f.
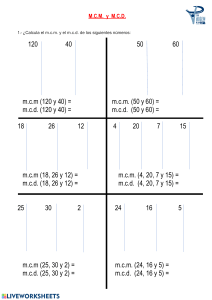

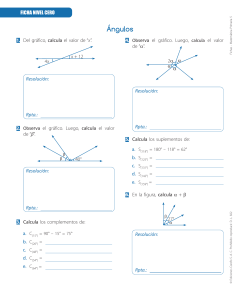

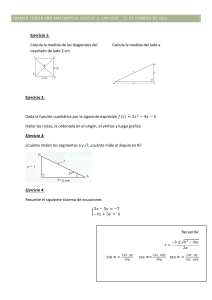
![Evaluación%20Grado%20Decimo%20noveno%20y%20undecimo[1].](http://s2.studylib.es/store/data/000860011_1-723727629aa8ab5007657ff23e4e4a09-300x300.png)